有色金属科学与工程  2018, Vol. 9 Issue (4): 53-59
文章快速检索     高级检索
引用本文
0
刘欣, 李强锋, 汪志刚, 张迎晖, 谢健明, 刘蔚宁. 低合金微碳钢的热变形行为及本构方程[J]. 有色金属科学与工程, 2018, 9(4): 53-59. DOI: 10.13264/j.cnki.ysjskx.2018.04.009.
LIU Xin, LI Qiangfeng, WANG Zhigang, ZHANG Yinghui, XIE Jianming, LIU Weining. Hot deformation behavior and constitutive equation of low alloy micro-carbon steel[J]. Nonferrous Metals Science and Engineering, 2018, 9(4): 53-59.DOI: 10.13264/j.cnki.ysjskx.2018.04.009.
低合金微碳钢的热变形行为及本构方程[PDF全文]
刘欣1 , 李强锋1 , 汪志刚1 , 张迎晖1 , 谢健明1 , 刘蔚宁2     
1. 江西理工大学材料科学与工程学院，江西 赣州 341000;
2. 国家电网公司交流建设分公司，北京 100083
基金项目：江西省重点研发计划项目(20161BBE50065);第59批中国博士后科学基金面上项目(2016M592101)
通信作者：汪志刚(1983-), 男, 博士, 副教授, 主要从事先进金属材料组织性能控制方面的研究, E-mail:wzgang2008cn@163.com
收稿日期：2018-03-14
摘要：在Gleeble-3800热模拟试验机上以微碳钢为研究对象，研究了在350 ℃、400 ℃、450 ℃、500 ℃、550 ℃、600 ℃、650 ℃、700 ℃、750 ℃和0.01 s-1、0.1 s-1、1 s-1条件下的热变形行为，并分析变形后的组织特征，构建温变形本构方程.结果表明，微碳钢的流变应力在变形初期随着应变的增大而增加，而在出现峰值后逐渐趋于平稳，当温度高于750 ℃时会出现明显的加工软化; 运用Sellars-Tegart方程，通过拟合模型中各参数, 获得微碳钢的热变形激活能Q为364.894 kJ/mol，并建立了流变应力模型.
关键词：微碳钢    热变形    流变应力    本构方程    显微组织    
Hot deformation behavior and constitutive equation of low alloy micro-carbon steel
LIU Xin1 , LI Qiangfeng1 , WANG Zhigang1 , ZHANG Yinghui1 , XIE Jianming1 , LIU Weining2     
1. School of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. State Grid Corporation of China, AC construction branch, Beijing 100031, China
Abstract: By applying Gleeble-3800 Thermal Simulation Tester, we study the thermal deformation behavior of micro-carbon steel at temperatures of 350℃, 400℃, 450℃, 500℃, 550℃, 600℃, 650℃, 700℃, 750℃ and under the conditions of 0.01 s-1, 0.1s-1, 1s-1. The temperature deformation constitutive equation is constructed by analyzing the characteristics of the deformed structure. The results show that the flow stress of micro-carbon steel increases with the rising strain in the initial stage of deformation, and gradually stabilizes after the peak. When the temperature is higher than 750℃, there will be obvious processing softening. With the Sellars-Tegart equation, the heat deformation activation energy Q of micro carbon steel was obtained by fitting the parameters of the model to 364.894 kJ/mol. A flow stress model is established.
Key words: micro-carbon steel    thermal deformation    flow stress    constitutive equation    microstructure    

微碳钢(0.01% < ωC < 0.03%)拥有较高的强度、塑性和深冲性能, 以及良好的焊接性和抗老化特性, 被广泛应用于汽车外覆盖件和部分结构件中。近年来, 随着乘用车车身材料轻量化需求的提高, 对先进汽车用钢的强度和深冲性能的优良匹配提出了更高的要求。传统无间隙原子(IF)钢, 由于超纯净钢质和超低碳含量, 使其具有优异深冲性能(r值> 2.0), 然而其抗拉强度较低(< 500MPa)。Hank-Som[1]和Yoshikita等[2]提出了在微碳的基础上通过控制第二相粒子析出发展深冲织构, 然而, 其最终的γ纤维织构强度仍低于IF钢。因此, 急需探索新型生产工艺进一步改善其深冲织构.

近些年, 温变形技术在IF钢和微碳钢中均有所研究和报道, 其中最为典型就是铁素体区轧制。铁素体轧制又称相变控制轧制, 通过铁素体晶内形成大量剪切带来诱发再结晶织构的形成, 可以大幅改善深冲性能[3-4]。目前铁素体轧制技术的研究主要集中在IF钢上, 微碳钢上由于存在典型动态应变时效(DSA)效应而未顺利推广[5-6]。除此之外, 微碳钢在温变形过程中的基本变形力学参数和模型尚需要深入探索和研究。康娅雪等[7]通过对微碳钢和微合金低碳钢进行了热变形行为研究, 得到了两个区域压缩的热变形方程。陈瑾等[8]通过研究微碳钢在铁素体区的热变形行为, 得到变形参数与变形抗力的关系, 从而建立了微碳钢温轧时的变形抗力模型。不同合金体系下的微碳钢, 变形本构方程仍存在一定差异。因此, 本文以Cr-Nb微合金化微碳钢为研究对象, 研究其热变形行为, 分析变形温度、应变速率对其组织演变的影响, 并确定流变应力方程, 进一步为实现微碳钢的温变形提供参数依据和理论依据.

1 实验材料及试验方法

实验材料为微碳钢, 其化学成分如下表 1所示.

表 1 实验材料的化学成分/(质量分数, %) Table 1 Chemical composition of the material/ (mass fraction, %)
点击放大

在热轧板中沿轧向取若干个Φ5mm×8mm的试样。在试样两端贴上石墨片作为润滑并在Gleebe-3800热模拟试验机上进行热压缩实验。在实验中, 压缩量为65%, 变形温度有350℃、400℃、450℃、500℃、550℃、600℃、650℃、700℃、750℃, 应变速率有0.01s-1、0.1s-1、1s-1, 升温速度为10℃/s, 升到实验温度后保温3min之后进行压缩实验。1s-1时在更低温度(650℃以下)压缩过程中因变形速率过大导致试样打滑, 所以在该应变速率下没有对更低的温度进行实验。在实验过程中Gleebe-3800热模拟试验机会自动采集所需的实验数据。试样在压缩后立即水淬, 以保留压缩后的原始组织, 图 1(a)为压缩后的试样图。之后使用Sigma型扫描电镜观察试样压缩变形后的组织。试样的端面与压头之间存在摩擦力所以试样在压缩后呈鼓型。试样压缩后的纵截面分为如图 1的三个区域。其中(Ⅲ)区的晶粒尺寸与实际工艺下的晶粒尺寸是最接近的, 所以在实验后取此区的中心位置作为试样组织观察区.

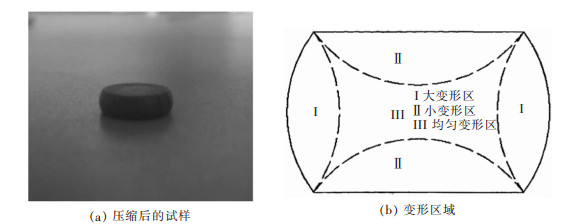图 1 热压缩后试样及示意图 Fig. 1 Hot compressed sample and schematic diagram

2 结果与讨论 2.1 真应变-真应力曲线

图 2为微碳钢的真应力-真应变曲线。由图 2可知, 流变应力值会先随着应变量的增加而迅速增大, 并迅速达到峰值。其原因是在变形初期交滑移为主要的软化机制, 而因交滑移引起的软化小于因加工硬化导致的硬化, 因此在变形初期加工硬化处于主导地位, 因此流变应力增大并迅速达到峰值[9]。在流变应力达到峰值后有些曲线趋于平稳, 但有些曲线会有小幅度的下降。其原因随着变形的继续进行因变形量引起的变形储存能成为晶粒再结的驱动力[10], 微碳钢开始发生动态回复和动态再结晶, 导致微碳钢的软化, 从而使应力应变曲线的斜率不断下降。变形量的再增加材料的软化程度与加工硬化会达到平衡, 流变应力达到最大值且保持平稳(温度在350~450℃); 在较高温度时材料发生动态再结晶, 使得材料的软化程度将大于加工硬化, 从而流变应力在达到最大值后应力会有小幅度的下降(温度在500~750℃)[11].

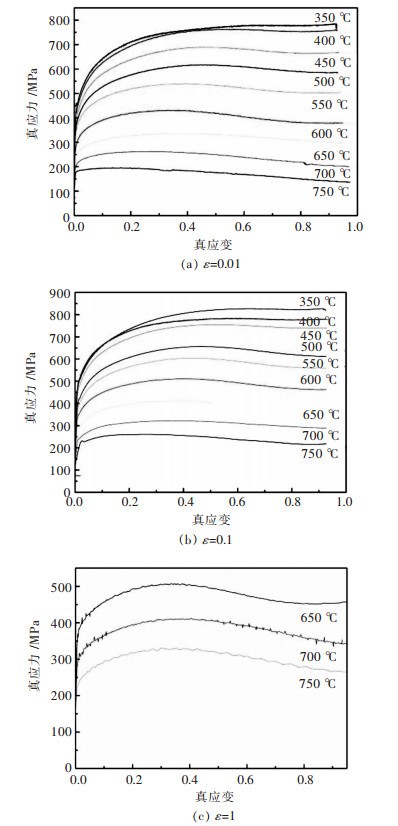图 2 微碳钢的真应变-真应力曲线 Fig. 2 True stress-strain curves of micro-carbon steelduring hot compression

对真应力—应变曲线进行非线性九次拟合。在真应力—应变曲线上, 一点的斜率定义为应变硬化率(θ), 对拟合的应力—应变数据进行微分即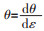。这样, 就可以得到各个应变(力)条件下的应变硬化率, 绘制得图 3(a)所示的应变硬化速率θ-σ图。应变硬化率会随着热变形过程的进行而逐渐减小, 且在θ-σ图中θ=0时的应力值为峰值应力σp[12]。从θ-σ图得到的各变形条件下的峰值应力可与变形温度、应变速率作得图 3(b)。从图中可知在同变形速率时, 峰值应力随着变形温度的升高而降低, 这是因为在低温下进行变形时, 加工硬化导致的硬化率高, 从而使得回复软化难进行。随变形温度的上升, 微碳钢的峰值应力会逐渐降低, 主要归因于温度升高, 使得空位原子扩散和位错运动的驱动力加大, 从而更易发生动态再结晶[13].

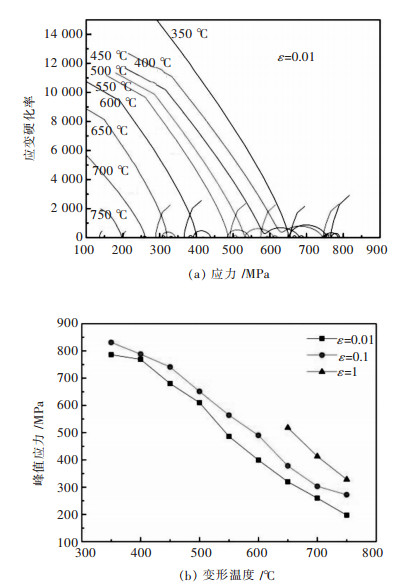图 3 应变硬化率θ-σ图和变形温度、应变速率对峰值应力的影响 Fig. 3 Strain hardening rate diagram (θ-σ)and Effects of deformation temperature and strain rate onpeakstress

2.2 热变形过程中组织的变化

图 4为微碳钢在不同工艺的组织, 其中图 4a到图 4d为相同应变速率不同温度下的组织。从图中可以看到, 温度在500℃(图 4a)时, 组织呈粗大的纤维状, 在500℃微碳钢发生了动态回复[13]; 在600℃(图 4b)时显微组织仍然呈纤维状, 并与500℃的相比更为细长, 表明在600℃时微碳钢仍然发生了动态回复但比之前的更完全。在700℃(图 4c)时, 发现试样的组织与之前的相似, 依然呈纤维状, 但存在少量的等轴晶粒, 这显示微碳钢在700℃时仍然发生了动态回复, 并有生成等轴晶粒的趋势。在750℃时, 发现大量的等轴晶粒, 在该温度下发生动态再结晶。这些现象说明在微碳钢的热变形行为中, 变形温度低时金属的主要软化机制是动态回复, 随着变形温度的上升, 动态回复发生越完全, 当超过临界温度时, 主要的软化机制转变为动态再结晶[13]。所以正如图 3所示一样, 随着变形温度的增加, 微碳钢的峰值应力是逐渐下降的.

图 4 微碳钢在不同变形条件下的组织形貌(SEM) Fig. 4 Microstructure of micro-carbon steel under different deformation conditions(SEM)

图 4d到图 4f为相同温度不同应变速率下的组织。从图中可以看到在应变速率小时(图 4e)有许多的细小的等轴晶粒和少部分纤维状组织的存在, 在此应变温度和应变速率下, 微碳钢发生了动态再结晶。在应变速率增大时(图 4d)组织仍然是等轴晶粒和纤维状组织, 但等轴晶粒含量比图 4e中的含量低, 而纤维状组织含量增加。应变速率再次增大时(图 4f)细小的等轴晶粒几乎观察不到, 组织主要为纤维状组织组织。在相同的变形温度(750℃)时, 随着应变速率的增加, 等轴晶数量越来越少, 动态再结晶的程度降低。这主要是因为, 变形速率的增加, 使得变形时间相应缩短, 而位错没有足够时间发生运动, 变形后的晶粒也不能及时发生回复与再结晶, 动态再结晶只在弯折晶界附近发生[14]。从而使得动态再结晶程度有所下降, 多边形化晶粒数目减少.

2.3 热变形的流变应力本构方程

通常利用材料在热变形过程各变形条件之间的联系来预测材料的成形过程。流变应力方程可以描述出材料在热变形过程中各变形条件之间的关系, 并在热变形中, 一般都用Sellars和Tegart提出的Sellars-Tegart关系式来描述温度和变形速率与流变应力之间的关系[15]:

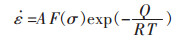
(1)

式(1)中, F(σ)是应力的函数, 大量的研究结果表明[16-17], 式(1)能较好地描述压缩、扭转等常规的热加工变形。式(1)有三种不同的表达形式:

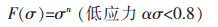
(2)
(3)
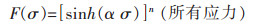
(4)
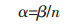
(5)

上式中Q代表热激活能; n代表应力指数; R代表气体常数; A代表结构因子; T代表绝对温度; 通过求Q、A和n, 就能获得材料的流变应力值。大量的研究结果表明可用Zener-Hollonmon参数来描述热变形条件[18]:

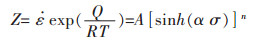
(6)

从上述公式(6)可以推导出如下公式:

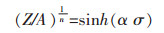
(7)

同时根据双曲正弦函数的定义, 可以得到:

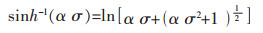
(8)

以上公式, 可以用变形温度和变形速率来表示流变应力方程函数, 同时也可用Z值的函数来表示流变应力, 其公式如下:

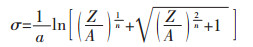
(9)

由公式(1)可得:

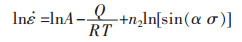
(10)

为了计算方便取相应的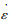、T条件下的峰值应力, 并分别以lnσ和σ为横纵坐标绘图, 得到图 5。对图 5进行最小二乘法进行线性回归, 其中图 5(a)中直线的斜率的平均值为n且n=19.7626;图 5(b)中直线的斜率的平均值为直线β且β=0.03566.

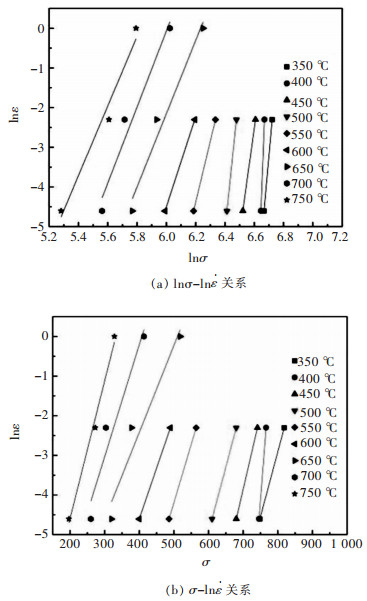图 5 lnσ、σ与ln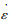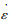的关系图 Fig. 5 Relationship between lnσ、σand ln

α值可通过公式=β/n求出, 计算得:

α=β/n=0.03566/19.7626=0.001804

在应变和应变速率不变时, 公式(10)对1/T求偏导:

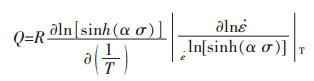
(11)
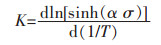
(12)

由式(11)可知, 在应变速率不变的条件下, ln[sinh(ασ)]与1/T为线性关系; 在变形温度恒定的条件下，ln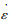与ln[sinh(α σ)]是线性的关系. K为直线1/T~ln[sinh(α σ)]的斜率; n2为直线ln[sinh(α σ)]~ln的斜率.

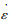
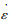
选取σ、相对应的T和，绘制1/T~ln[sinh(α σ)]图和~ln[sinh(α σ)]~ln图，如图 6所示.对其进行最小二乘法线性回归，得图 6(a)中直线斜率的平均值K，其值K=3.370 1;得图 6(b)中直线斜率的平均值n2，其值n2=13.023 1.从而得到Q=RKn2=8.314×3.3701×1000×13.0231=364.894 kJ/mol.

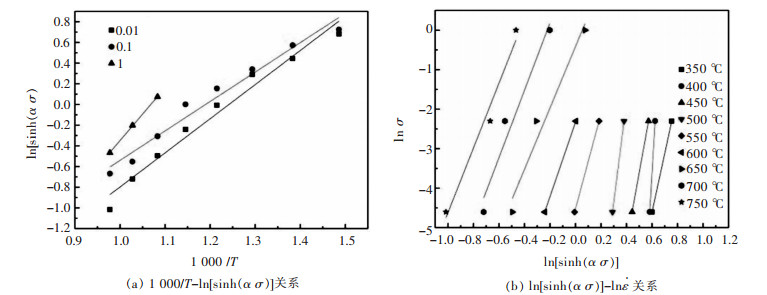图 6 ln[sinh(α σ)]与1000/T、ln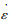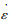的关系 Fig. 6 Relationship between ln[sinh(α σ)] and、1000/T、ln

由公式取对数得:

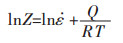
(13)
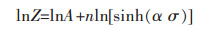
(14)

式(14)中, lnA为直线ln[sinh(α σ)]~lnZ的截距。当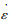、Q与T已知时, 可以求得lnZ值。如图 7所示绘制ln[sinh(α σ)]~lnZ图, 并对此数据进行最小二乘法线性回归, 线性拟合得:lnZ=50.531+16.021ln[sinh(α σ)], 故lnA=50.531, 则A=8.817×1021.

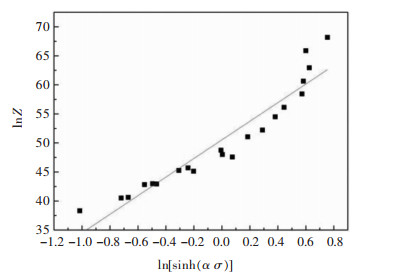图 7 ln[sinh(α σ)]与lnZ的关系图 Fig. 7 Relationship between ln[sinh(α σ)] and lnZ

将上述得到的参数带入公式(9)中, 得到微碳钢的流变应力方程为:

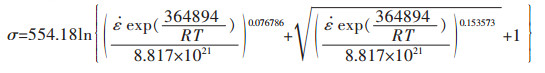
(15)

通过流变应力方程计算的峰值应力与实际峰值应力之间的误差较小, 说明此流变应力方程有较高的准确性.

本文通过模拟的方法得到了微碳钢温轧时的变形抗力模型, 为温轧力的计算提供了依据, 为微碳钢的温轧生产提供理论指导.

3 结论

1) 通过试验获得低合金微碳钢的真应力-真应变曲线。随着应变速率的增大, 流变应力逐渐增加。随着变形温度的升高, 流变应力逐渐降低。在同等条件下, 低应变速率(0.01s-1)和高变形温度(750℃)使得微碳钢易发生动态再结晶.

2) 通过构建了微碳钢的流变应力方程, 计算出其激活能Q为364.894KJ/mol。其流变应力方程为:
参考文献
[1]
SEONGH H, SHIHC, JAEK C, et al. Effect of hot-rolling processing on texture and r-value of annealed dual-phase steels[J]. Materials Science and Engineering A, 2010, 527(7/8): 1686–1694.
[2]
HIROMI Y, KANEHARU O, HIDETAKA K, et al. Effect of niobium addition on the texture formation of high strength cold-rolled low carbon steel sheets[J]. Materials Science Forum, 2007, 558/559: 425–430. DOI: 10.4028/www.scientific.net/MSF.558-559.
[3]
LIU DS, HUMPHREYS A O, TOROGHINEZHAD MR, et al. The Deformation Microstructure and Recrystallization Behaviorof Warm Rolled Steels[J]. ISIJ International, 2002, 42(7): 751–759. DOI: 10.2355/isijinternational.42.751.
[4]
YAZAWAY, MURAKIM, KATOY, et al. Effect of Chromium Content on Relationship Between r-valueand{111} Recrystallization Texture in Ferritic Steel[J]. ISIJ International, 2003, 43(10): 1647–1651. DOI: 10.2355/isijinternational.43.1647.
[5]
ZHANG P, GUO YH, WANG ZD, et al. Texture evolution in ferritic rolled Ti-IF steel during cold rolling[J]. Journal of Iron and Steel Research, International, 2010, 17(1): 44–48. DOI: 10.1016/S1006-706X(10)60043-X.
[6]
GUO YH, WANG ZD, ZOU WW, et al. Textures and properties of hot rolled high strength Ti-IF steels[J]. Journal of Iron and Steel Research, International, 2008, 15(5): 70–76. DOI: 10.1016/S1006-706X(08)60252-6.
[7]
康娅雪, 蔡大勇, 张春玲, 等. 微碳钢的热变形方程及热加工图[J]. 材料热处理学报, 2012, 33(6): 74–79.
[8]
陈瑾, 陆鑫, 杨艳军, 等. 微碳钢铁素体区轧制的变形抗力模型[J]. 河北理工大学学报(自然科学版), 2011, 33(2): 52–56. DOI: 10.3969/j.issn.1674-0262.2011.02.012.
[9]
周家林, 余茹, 余锰, 等. Ti-Mo-V微合金化钢的热变形行为[J]. 金属热处理, 2015, 40(4): 26–30.
[10]
曹淑芬, 张立强, 郭鹏程, 等. 22MnB5热变形行为研究及本构方程建立[J]. 中国机械工程, 2014, 25(9): 1256–1261. DOI: 10.3969/j.issn.1004-132X.2014.09.022.
[11]
余冲, 赵刚, 鲍思前, 等. 50CrV4奥氏体变形流动应力的研究[J]. 热加工工艺, 2013, 42(2): 20–23.
[12]
吴晋彬, 刘国权, 王浩, 等. SCM435钢热变形动态再结晶动力学模型参数的确定[J]. 北京科技大学学报, 2010, 32(10): 1282–1286.
[13]
沈耀红, 张志清, 覃丽禄, 等. 7085铝合金热压缩变形的流变应力本构方程[J]. 材料导报, 2011, 25(2): 127–130.
[14]
程晨, 雷旻, 万明攀, 等. BT25钛合金高温变形行为[J]. 有色金属科学与工程, 2017, 8(6): 51–56.
[15]
SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. ActaMetall, 1966, 14(9): 1136–1138.
[16]
AIROD A, VANDEKINDEREN H, BARROS J, et al. Constitutive equations for the room temperature deformation of commercial purity aluminum[J]. J Mater Proc Techn, 2003, 134(3): 398–404. DOI: 10.1016/S0924-0136(02)01129-9.
[17]
WRIGHT R N, PAULSON M S. Constitutive equation development for high strain deformation processing of aluminum alloys[J]. J Mater Proc Techn, 1998, 80/81: 556–559. DOI: 10.1016/S0924-0136(98)00158-7.
[18]
ZENER C, HOLLOMON J H. Effect of stain-rate upon the plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22–27. DOI: 10.1063/1.1707363.