| COREX熔融气化炉炉缸流场研究 |
COREX工艺是由德国科夫(KORF)公司与奥钢联(VAI)公司联合开发的可以摆脱高炉对烧结矿和高质量焦炭要求的熔融还原工艺[1, 2].COREX工艺与高炉相比具有无需烧结、炼焦工艺排放低的特点,在环保方面具有很大的优势[3-5].我国新疆全区铁矿石预测资源总量约为87.9亿t,占全国预测资源总量的14.5%.新疆八钢自己拥有的矿山铁矿石探明储量达9.22亿t,拥有艾维尔沟煤矿、石灰石、白云石等矿产资源,储量丰富,自给率可达到100%.考虑到新疆地区的资源优势,近年来宝钢将C-3000迁建新疆八钢,在缓解八钢每年270万t铁水缺口的同时,更好的促进了COREX工艺的发展[6].
COREX工艺是一种兼具竖炉和煤气化利用特点的较成熟的工艺.该工艺系统主要由熔融气化炉,预还原炉,加料设备与尾气处理等附属设备组成.其中熔融气化炉替代了高炉的炉腹和炉缸,经竖炉预还原得到的海绵铁,在熔融气化炉内进一步还原、融化,造渣,并使得到的铁水达到最终的温度和成分的要求[7-12].因此,可以说熔融气化炉是COREX工艺的关键,也是该工艺发展的限制性环节.
相比于高炉,熔融气化炉对固体燃料的强度以及粒度要求较低,炉内料柱的透气性更易恶化[13].熔融气化炉炉缸耐火材料的破损被广泛认为是制约COREX熔融气化炉使用寿命的主要限制因素,其损坏形式主要包括化学侵蚀、热侵蚀和机械侵蚀等[14].此外,COREX熔融气化炉采用纯氧鼓风,使得炉缸温度比高炉高很多.在炉缸铁水流动方面,熔融气化炉与高炉相比也有不同之处,并且COREX在出铁过程中,存在二次铁流现象,二次铁流对出铁口的侵蚀极为严重,在实际生产中应有效的抑制二次铁流的发生.综上所述,对熔融气化炉炉缸中铁液的流动状态及热流转换进行研究是很有必要的.然而,炉缸内的实际情况是非常复杂的,不可能进行直接测量,只能通过仪表进行间接测量.近年来,随着计算机及数值模拟技术的发展,对炉缸进行数学建模,并利用模拟软件对炉缸内铁水流动和温度分布状态进行仿真成为常用的研究手段[15].
以八钢COREX C-3000熔融气化炉炉缸作为研究对象,使用FLUENT模拟软件,建立三维炉缸铁水流动数学模型,主要针对不同条件下(包括死料柱沉坐与浮起、出铁口直径大小、出铁口角度等不同条件下)炉缸铁水流动进行数值计算与分析,并利用物理模型(即水模型)对结论进行验证.通过对计算结果进行比较分析,得出适宜的出铁操作条件,为现场生产提供参考,以达到延长炉缸使用寿命的目的.
1 模型设计 1.1 假设条件由于熔融气化炉炉缸内铁水流动情况十分复杂,为了方便计算,降低非主要因素的影响,在建立炉缸铁水流动数学模型时,做了如下假设:
1) 假设炉缸内型和死料柱的形状都是圆柱形;
2) 假设铁水为不可压缩的连续性流体,且仅考虑铁水的流动,流动近似为三维定常流动,不计算炉缸内铁水液面的波动;
3) 忽略COREX熔融气化炉炉缸耐火材料与铁水间的物理、化学反应以及炉渣对耐材的影响;
4) 以COREX熔炼率(t/h)作为入口质量流量边界条件,垂直入口平面向下.
1.2 数学模型模型的控制方程包括质量守恒方程、动量守恒方程、湍动能方程和湍动能耗散方程,通过对以上方程的联立求解得到炉缸内铁水流动的速度分布状况.
1) 连续性方程
| $ \frac{{\partial \rho {u_i}}}{{\partial {x_i}}} = 0 $ | (1) |
式(1)中:ρ为流体密度,kg/m3; ui为张量表示的时均速度,m/s
2) 动量传输方程(Navier—Stokes方程)
| $ \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} =- \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[{{\mu _{eff}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] $ | (2) |
式(2)中:ui,uj为i,j方向的速度,m/s;xi,xj—i,j方向的坐标值,m;ρ为流体密度,kg/m3;P为压力,Pa;μeff为有效年黏度系数,Pa⋅s,可用湍流模型确定.
湍流模型采用Lauder和Spalding的k-ε双方程模型.
3) 湍动能(k)方程
| $ \frac{\partial }{{\partial {x_i}}}\left[ {\rho {u_i}k - \frac{{{\mu _{eff}}}}{{{\sigma _k}}} \cdot \frac{{\partial k}}{{\partial {x_i}}}} \right] = {G_k} - \rho \varepsilon $ | (3) |
式(3)中:k为湍流动能,m2/s2;ε为湍流动能耗散率,m2/s3;
4) 湍动能耗散率(ε)方程
| $ \frac{\partial }{{\partial {x_i}}}\left[{\rho {u_i}\varepsilon-\frac{{{\mu _{eff}}}}{{{\sigma _k}}} \cdot \frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right]{\rm{ = }}\left( {{C_i}\varepsilon {G_k} -{C_2}\rho {\varepsilon ^2}} \right)/k $ | (4) |
其中:
式(4)中:有效黏度系数μeff=μ1+μt,μt为湍流黏度系数,Pa⋅s;μ1为层流黏度系数,Pa⋅s;
C1,C2,Cμ,为经验常数,采用Launder和Spalding的推荐值,如下:
C1=1.44, C2=1.92, Cμ=0.09, σk=1.0,
模型采用的边界条件为:
1) 入口边界:质量流量入口,通过出铁口的日出铁流量换算得到;
2) 出口边界:采用压力出口(pressure-outlet)边界条件;
3) 炉缸壁面:炉缸壁面采用无滑移边界条件,对壁面附近黏性底层中的流体采用FLUENT中的标准壁面函数进行处理[16-20];
4) 多孔介质:根据死料柱孔隙度和焦炭粒径等数据,通过厄根方程计算出惯性阻力系数和黏性阻力系数,作为动量方程的源相.
1.4 物理模型模拟的模型以八钢COREX C-3000炉缸为研究对象,铁水液面高度4m,死铁层深度2.4m,炉缸直径9.4m,出铁口直径0.050m,出铁口倾角7°,铁水平均质量流量为150t/h,铁水密度7000kg/m3,铁水黏度0.0067Pa⋅s.死料柱孔隙度分布是不均匀的,中心部位更新较慢,孔隙度最小,且根据原料和生产状况的不同,死料柱孔隙度也有所不同,平均约为0.3~0.4.八钢COREX的炉缸物理模型如图 1所示,其中内部线框表示死料柱,是一个直径小于炉缸直径的圆柱,在炉缸壁处,由于“容壁效应”,孔隙度很大,可认为容壁处存在狭小缝隙.
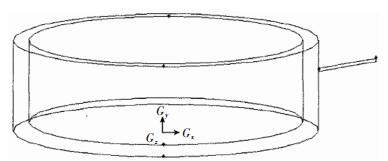 |
| 图 1 炉缸物理模型 Fig. 1 physical model of hearth |
在计算过程中需要兼顾计算精度和计算效率问题,网格过粗不能反映出真正的流动状态,还可能造成迭代过程发散;而网格过密又会大大增加计算机运算次数,导致舍入误差增加.因此,必须选择合适的网格数进行模拟.本模拟网格数目大约为20万个六面体/四面体网格,网格划分如图 2所示.
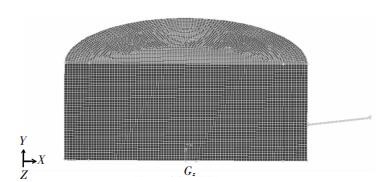 |
| 图 2 模型网格划分 Fig. 2 Model meshing |
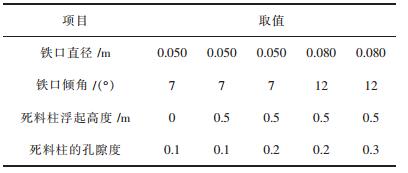
模拟计算的参数如表 1所示,取值参考了八钢COREX C-3000熔融气化炉炉缸的实际生产数据.为了方便模拟对比,采用控制变量法,通过计算分析得出适宜的出铁操作条件,为现场生产提供参考,以达到延长炉缸寿命的目的.
| 表 1 模拟计算的参数及取值 Table 1 Calculation parameters and values |
 |
| 点击放大 |
2 计算结果及分析 2.1 死料柱“浮起”与“沉坐”对铁水流场的影响
在不同操作条件及死铁层深度下,死料柱在炉缸内可能“沉坐”,也可能“浮起”,其示意图如图 3所示.不同的存在状态将对炉缸内的铁水流动路径产生影响.图 4和图 5分别从水平和垂直切面两个角度给出了死料柱在铁水中“沉坐”与“浮起”(浮起高度0.5m)时的铁水流场示意图.
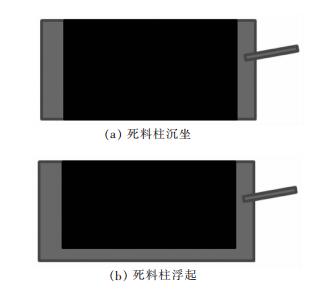 |
| 图 3 死料柱情况示意图 Fig. 3 Schematic diagram of existing state of deadman |
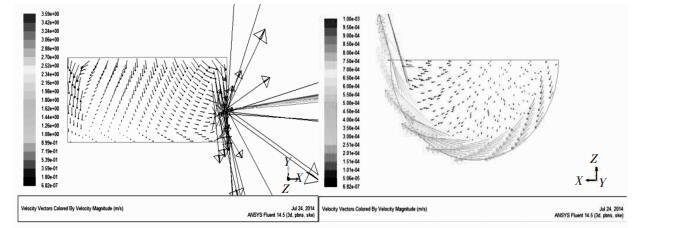 |
| 图 4 死料柱“沉坐”时的铁水流场图 Fig. 4 Flow distribution of hot metalwhen deadman sitting on the bottom |
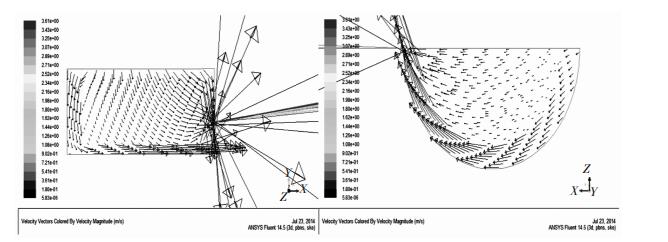 |
| 图 5 死料柱“浮起”0.5m时的铁水流场图 Fig. 5 Flow distribution of hot metal when deadman is floating at a height of 0.5 m |
比较图 4和图 5的铁水流场图可以看到:当死料柱浮起时其与炉底之间会出现自由空间,从而使铁水的流动路线发生改变,铁水向下通过没有焦炭的自由空间,形成垂直方向的铁水环流,最终从出铁口流出.通过炉底狭小空间的铁水流量明显较死料柱沉坐时的流量大,且流速加快,对炉底会造成一定的冲刷,但铁水在无焦空间的流动,减小了水平方向的铁水环流,其流速降低1-2个数量级,因此对炉缸侧壁尤其是“象脚”部位的冲刷会大大减弱,而从炉缸破损调查统计来看,炉缸损坏主要集中在炉缸侧壁和“象脚”部位,而极少见炉底的冲刷侵蚀破坏,因此死料柱的浮起对于减少水平方向环流的作用更应该受到重视.
为进一步对铁水流场的计算结果进行对比分析,在距离炉底底面0.1m处取一条直线(图 1中,距底面高0.1m处中心的一条直线y=0.1,z=0,-5 < x < 5),对该直线上的铁水流速进行比较,如图 6所示.可以看到当死料柱“浮起”时,炉底的铁水流速明显大于死料柱“沉坐”时的铁水流速,且越接近出铁口,流速差距越大,其值为几十到几百倍之间.
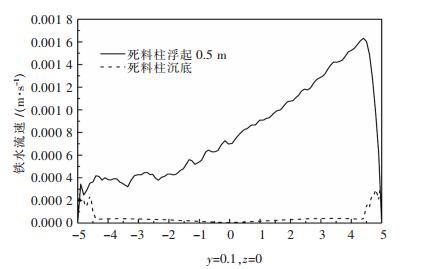 |
| 图 6 死料柱沉坐和浮起0.5m时的铁水流速 Fig. 6 Comparison of velocity of hot metal between deadman sitting and floating (0.5 m height) |
2.2 死料柱孔隙度对铁水流场的影响
不同的原料条件和操作制度会影响死料柱物理结构以及其更新周期,最终导致死料柱孔隙度的变化,影响其透气透液性,进而影响铁水的流动状态.采用控制变量法,模拟了相同铁口直径、铁口倾角、死料柱浮起高度条件下,死料柱孔隙度Φ分别为0.1、0.2、0.3(垂直切面)时的铁水流场,结果如图 7所示.
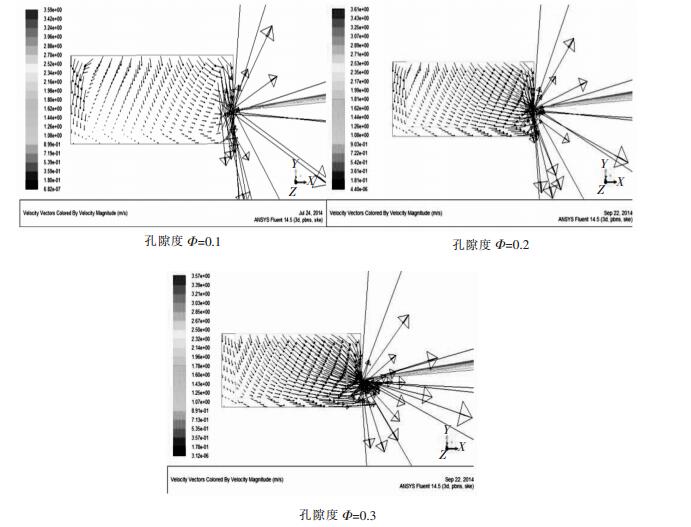 |
| 图 7 不同孔隙度下的铁水流场图(垂直切面) Fig. 7 Flow distribution of hot metalat different porosities (vertical section) |
随着死料柱孔隙度的增大,通过死料柱的铁水流量逐渐增加,铁水流速也随之提高,表现为死料柱内部的速度矢量长度增大.这是因为死料柱孔隙度越大,铁水在其内部流动遇到的阻力越小,流动加快,从而会使其铁水流量增加.同时,在炉缸侧壁的铁水流速降低,减小了对炉缸侧壁的冲刷.
在实际生产条件下,如果燃料形成的半焦强度差、粒度小、长时间休风或存在不良的炉缸结构等,都会导致死料柱“不活”(即孔隙度较小).如果死料柱中心堵塞,将会导致铁水大量靠近侧壁流动,从而会使炉底和炉缸侧壁受到一定的冲刷侵蚀.因此,适当增加死料柱的孔隙度,炉缸内的铁水环流作用会减弱,有助于降低铁水对炉底和炉缸侧壁的冲刷侵蚀[21].
2.3 铁口直径对铁水流场的影响不同的出铁口直径对应的出铁流量不同,会对炉缸内铁水流场产生一定的影响.炉缸铁口直径越大,铁水质量流量越大,流速也会发生变化.模拟了铁口直径为0.050m和0.080 m时的铁水流动状况,如图 8所示.
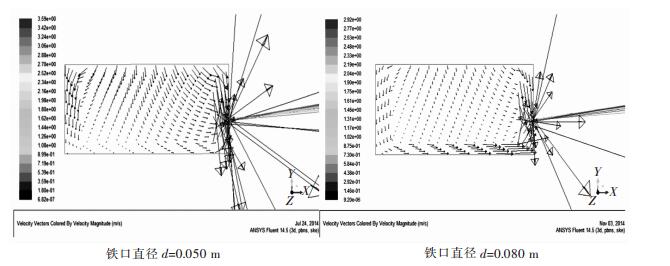 |
| 图 8 不同铁口直径下的铁水流场图(垂直切面) Fig. 8 Flow distribution of hot metal at different tap hole diameters (vertical section) |
对比图 8中两种铁口直径下铁水流场示意图,从整体上来看,随着铁口直径增大,炉内铁水流速增加,环流加剧.尤其在靠近铁口附近,流速增加更加明显.通过对炉底铁水流速分布进行比较,如图 9所示,可以看出:当出铁口直径由0.050m增大到0.080 m时,铁水排放速度随之增加,出铁量增大,铁水环流对炉底和炉缸侧壁的冲刷侵蚀加剧.随着铁水向铁口方向流动,速度差距逐渐增大,在近铁口方向半径为4.5米左右处,速度差距达到最大,增大约0.7倍.
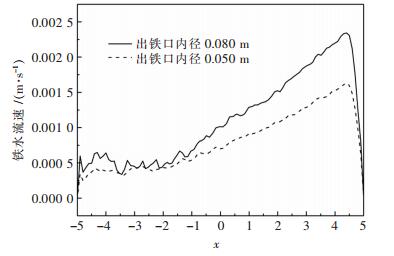 |
| 图 9 不同铁口直径下的铁水流速 Fig. 9 Velocity of hot metal at different tap hole diameters |
2.4 铁口角度对铁水流场的影响
图 10给出了不同铁口倾角下铁水在距离炉底0.1m高度沿直径方向的流速分布.可以看出,不同的出铁口倾角(7°和12°),对该部位铁水的流速影响不大.且流速沿直径方向的变化趋势也相同,在相同位置同时达到峰值.因此,出铁口角度由7°变化到12°时对炉底铁水流速的影响可以忽略.
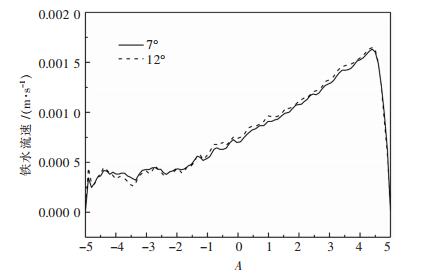 |
| 图 10 不同铁口角度下铁水流速沿直径的变化 Fig. 10 Varies of hot metal velocity with diameter at different tap hole angles |
3 物理模型验证
应用FLUENT软件模拟了不同条件下(死料柱沉坐与浮起、空隙率大小、出铁口直径、出铁口角度等)COREX C-3000熔融气化炉炉缸内铁水流动状况,分析得出了一些结论.为了验证模拟结果的正确性,进行了水模实验验证.
炉缸的水模型模拟装置示意图如图 11所示.为保证铁水由软熔带滴落至炉缸的过程中在炉缸平面上的流速分布均匀,在水模拟实验装置中设置了水流分配器,进水口被分为16个支流,以更加真实的模拟铁水滴落的过程.
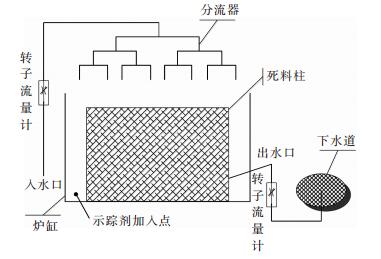 |
| 图 11 炉缸的水模型装置示意 Fig. 11 Schematic diagram of the water model |
实验装置如图 12所示,死料柱的材质为透明玻璃球,其孔隙度约为0.3,以圆柱形塑料装置代替炉缸,实验过程中通过转子流量计控制入水口的流量,入水流量控制在15~20 L/min范围内,使液面维持在一个稳定的高度.以红色墨水作为示踪剂,实验中通过观察红色墨水的流动状况来模拟不同参数对铁水流动状态的影响.
 |
| 图 12 炉缸的水模型实际装置图 Fig. 12 Schematic diagram of the water of the hearthmodel of the hearth |
为了验证数值模拟的正确性,针对不同出铁口直径进行实验比较.两组出口的管径分别为1.2cm与1.0cm.出口打开前,加入红色墨水作为示踪剂,打开排水口,直观比较两种出口直径下的铁水环流状况,如图 13、14所示.与模拟结果对比可以看出,管径为1.2cm、1.0cm的实验现象与数值模拟中出铁口直径为0.080m、0.050m的铁水流动趋势基本一致,从而验证了数学模型所得结论的正确性.
 |
| 图 13 不同出口直径下出水示踪图(正视图) Fig. 13 Flow state of water at different outlet diameters (front view) |
 |
| 图 14 不同出口直径下出水示踪图(俯视图) Fig. 14 Flow state of water at different outlet diameters(top view) |
4 结论
采用数值模拟方法计算了不同条件下COREX炉缸铁水的流场,并应用水模型对模拟结果进行了验证.得出如下结论:
1) 铁水环流是造成炉缸侵蚀的主要原因之一,死料柱过大或死料柱孔隙度偏小是造成铁水环流的主要因素.当死料柱“浮起”时,其与炉底之间会形成无焦的自由空间,从而铁水的流动路线会发生改变,铁水通过没有焦炭的自由空间,从铁口流出,致使通过狭小空间的铁水流量明显增大,铁水流速加快,对炉底造成一定的冲刷;但炉底铁流的增加,减缓了炉缸水平方向的铁水环流,进而减小了炉缸侧壁尤其是象脚部位的冲刷侵蚀,这显得更有意义.同时,随着炉底无焦区的增大,炉底铁水流速也会降低.
2) 死料柱的孔隙度影响了死料柱的透气性和透液性,孔隙度越大,铁水在其内部流动遇到的阻力越小,流动越快,边缘环流作用减弱,对炉缸侧壁的冲刷侵蚀减弱.因此改善中心死料柱的孔隙度,有利于保护炉缸、炉底,延长使用寿命,提高生产效率.
3) 减小出铁口直径,可以降低出铁速度,延长出铁时间,炉缸内部铁水环流作用降低,对炉缸侧壁和炉底的侵蚀冲刷作用减小.实际的COREX炉缸应根据压力大小、炮泥质量、出铁速度来选择适宜的出铁口直径.此外,出铁口倾角的变化对铁水流场的影响很小.
4) 通过水模型实验验证了数值模拟的正确性.
| [1] |
周渝生, 钱晖. COREX熔融还原炼铁新工艺[J].
世界钢铁, 2005, 5(1): 22–26.
|
| [2] |
方觉.
非高炉炼铁工艺与理论[M]. 北京: 冶金工业出版社, 2010.
|
| [3] |
张冶. 建设绿色环保、节能、循环利用资源的新型钢铁厂[J].
钢铁, 2007, 42(1): 76–80.
|
| [4] |
高渝纲. 关于发展熔融还原炼铁技术的思考[J].
中国钢铁业, 2007, 1(5): 33–35.
|
| [5] |
吴俐俊, 苏允隆. COREX炼铁法的现状及发展前景[J].
钢铁, 1996, 31(9): 69–74.
|
| [6] |
林成城, 项钟庸. 宝钢高炉炉型特点及其对操作的影响[J].
宝钢技术, 2009, 2(11): 49.
|
| [7] |
杜开平, 赵世强, 吴胜利. 熔融气化炉风口回旋区冶炼特征的数值模拟研究[J].
有色金属科学与工程, 2017, 8(2): 8–13.
|
| [8] |
PICHESTAPONG P. Non-coke smelting reduction of iron ores: Process modelling[J].
Dissertation Abstracts International, 1997, 58(6): 32–65. |
| [9] |
AGRAWAL R, CHEN S K, SMITH A R, et al. High temperature oxygen production for ironmaking processes: US, US 5643354 A[P]. 1997-01-07.
|
| [10] |
程树森, 杨天钧, 薛庆国, 等. 长寿高炉设计指标及设计方案评价系统初探[J].
钢铁, 2000, 35(5): 10–15.
|
| [11] |
CHATTERJEE A. A critical appraisal of the present status of smelting reduction -Part 1fromblast furnace to Corex[J].
Steel Times International, 2005, 29(4): 23–26. |
| [12] |
CHATTERJEE A. A critical appraisal of the present status of smelting reduction-Part 2 Potential commercial smelting reduction processes[J].
Steel Times International, 2005, 29(4): 36–42. |
| [13] |
湛文龙, 吴铿, 徐万仁, 等. COREX熔融气化炉内料柱的透液性指数及影响因素[J].
北京科技大学学报, 2014, 36(9): 1241–1246.
|
| [14] |
李晓清, 王臣, 储文. COREX气化炉炉缸侵蚀模型的预测与实践[J].
宝钢技术, 2014, 32(4): 6–10.
|
| [15] |
周晓雷, 罗志国, 韩立浩, 等. COREX熔融气化炉软熔区域的试验研究[J].
中国冶金, 2011, 18(6): 9–14.
|
| [16] |
张先棹.
冶金传输原理[M]. 北京: 冶金工业出版社, 1988.
|
| [17] |
沈颐身, 李保卫, 吴懋林.
冶金传输原理基础[M]. 北京: 冶金工业出版社, 2000.
|
| [18] |
周波. COREX熔融还原工艺熔化气化炉炉缸区域模拟仿真研究[D]. 沈阳: 东北大学, 1999.
|
| [19] |
LUO Z G, ZHOU H, ZHANG T, 等. DEM simulation of solid flow including asymmetric phenomena in COREX shaft Furnace[J].
钢铁研究学报:英文版, 2015, 22(12): 1098–1106.
|
| [20] |
周波, 邹宗树. COREX熔化气化炉炉缸区域数值模拟仿真(Ⅰ)[C]//全国冶金反应工程学术会议. 沈阳: 东北大学, 1998.
|
| [21] |
国宏伟, 刘一力, 陈伟伟, 等. 高炉死料柱孔隙度变化对炉缸炉底流场的影响[C]//全国炼铁生产技术会议暨炼铁学术年会. 北京: 中国金属学会, 2009.
|
 2018, Vol. 9
2018, Vol. 9


