基于原子-分子理论的二元合金熔体热力学计算

引用本文

段生朝, 郭汉杰, 郭靖, 鲁浩, 石骁, 杨文晟, 刘帅, 于梦曦. 基于原子-分子理论的二元合金熔体热力学计算[J]. 有色金属科学与工程, 2017, 8(3): 7-15. DOI:10.13264/j.cnki.ysjskx.2017.03.002. 复制到剪切板

DUAN Shengchao, GUO Hanjie, GUO Jing, LU Hao, SHI Xiao, YANG Wensheng, LIU Shuai, YU Mengxi. Thermodynamic calculating of binary alloy melts based on atom-molecule theory[J]. Nonferrous Metals Science and Engineering, 2017, 8(3): 7-15.DOI: 10.13264/j.cnki.ysjskx.2017.03.002. 复制到剪切板

基于原子-分子理论的二元合金熔体热力学计算

[PDF全文]

段生朝, 郭汉杰, 郭靖, 鲁浩, 石骁, 杨文晟, 刘帅, 于梦曦

北京科技大学冶金与生态工程学院，高端金属材料特种熔炼与制备北京市重点实验室，北京 100083

基金项目：国家自然科学基金重点资助项目（U1560203）；国家自然科学基金资助项目（51274031）

作者简介：

收稿日期：2016-11-18

摘要：分别使用Miedema、MIVM、NRTL、Wilson二元合金系热力学模型及FactSage热力学软件计算Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn 4个二元合金系的活度值，并与实验值进行比较.结果表明：Miedema、MIVM、NRTL、Wilson模型计算不同体系活度的效果不同，每种模型都有其适用的体系.而FactSage热力学软件计算的活度均与实验值吻合较好，文中使用FactSage分别计算Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn 4个二元系不同温度下的活度值.同时利用原子-分子理论计算Bi-Pb二元系质量作用浓度，给出生成金属间化合物BiPb反应的标准吉布斯自由能的表达式.

关键词：二元合金 FactSage 原子-分子理论热力学活度

Thermodynamic calculating of binary alloy melts based on atom-molecule theory

DUAN Shengchao, GUO Hanjie, GUO Jing, LU Hao, SHI Xiao, YANG Wensheng, LIU Shuai, YU Mengxi

School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing Key Laboratory of Special Melting and Preparation of High-End Metal Materials, Beijing 100083, China

Abstract: The activities in Bi-Pb, Bi-Sn, Cd-Pb, Pb-Sn binary alloy system were calculated by Miedema model, molecular interaction volume model (MIVM), non-random two-liquid (NRTL) equation and thermodynamic modeling software FactSage respectively, and compared with measured value. The experimental results show that the Miedema model, MIVM model, NRTL model, Wilson model are not applicable to the above-mentioned four binary alloy system. But the measured activities has good corresponding with the calculated activities by thermodynamic modeling software FactSage, and the activities are calculated by using FactSage at different temperature. Meanwhile, a thermodynamic model for calculating the mass action concentration of structural units in Bi-Pb binary alloy system based on the atom-molecule coexistence theory has been developed, and the expression of standard Gibbs free energy change of reaction for forming intermetallic molecules as BiPb was put forward.

Key words: binary alloy FactSage atom-molecule theory thermodynamics activity

溶液热力学参数是冶金、化工、医药等领域进行新工艺研发、过程优化及理论研究使用的基础数据^[1].金属合金热力学性质对体系各组元活度依赖性是冶金热力学研究的重要方面^[2].测量金属合金溶液活度的方法通常有蒸气压法^[3]、凝固点降低法^[4]、化学平衡法^[5-6]、分配平衡法^[7]、电动势法^[8]等.而由于高温实验操作具有复杂性，实验测量具有困难性等特点，这使得到的热力学数据存在较大偏差.因此，利用理论或半经验数学模型对溶液热力学性质进行预测就显得十分重要.

近年来，诸多国内外科学家在溶液热力学研究方面做了大量工作. Raoult定律和Henry定律最早表述了二元溶液等温热力学行为^[9]；Darken将溶液分为不同区域，即存在线性关系的极端区和难以利用简单关系表达的中间区^[10]；1964年，Wilson^[11]得到局部分子分数与Boltzmann因子的关联式推导出Wilson方程；1968年，Renon^[12]和Prausnitz基于局部浓度的概念的半经验方程提出NRTL方程；1973年，Miedema等^[13]将Wigner-Seitz的元胞模型运用到二元合金中，提出经验理论模型Miedema模型.张鉴^[14]等进一步完善前苏联学者丘依理论的础上提出原子-分子理论模型(AMCT-Ni)，通过计算二元系熔体中结构单元的质量作用浓度，建立表征其反应能力；Bale^[15]和Eriksson提出集成热力学数据库的概念，基于这一概念，FactSage成为当今世界上最重要的热力学数据库和计算软件，且使用SGTE等国际上知名数据库，为模拟和计算众多复杂热力学体系提供了可能.

文中分别利用上述模型计算Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn 4个二元系在全浓度范围内的活度，并与实验测量值进行比较.其中Bi-Pb二元合金系生成金属间化合物BiPb，利用原子-分子理论通过计算二元系熔体中结构单元的质量作用浓度，并给出化合物BiPb的标准吉布斯自由能，为许多领域进行新工艺开发、过程优化及理论研究提供可靠的基础数据.

1 热力学模型计算

近年来，元素周期表中IIIA-VA族元素已广泛用作电子材料，因此对这些元素组成的合金材料的物理、化学性质有必要作深入研究.由于Bi-Pb、Bi-Sn、Cd-Pb及Pb-Sn二元合金系活度的测量值公认是可靠的^[16]，所以文中分别利用Miedema、MIVM、NRTL、Wilson模型计算值^[1]及FactSage热力学软件计算上述4个二元合金系的活度并与其实测值进行比较，通过分析得到不同模型对二元合金系活度预测值的准确性.二元合金系中每一个组元活度实测值与计算值的关系见图 1~图 4.

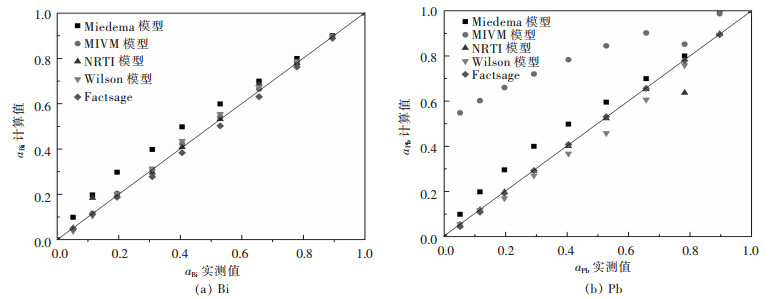图 1 Bi-Pb二元合金系活度a_Bi、a_Pb的实测值与其计算值的关系 Fig. 1 Relationship between measured activity a_Bi, a_Pb and calculated activity in full composition range of Bi-Pb binary melts by Miedema model, MIVM equation, NRTL equation, Wilson equation, FactSage, respectively

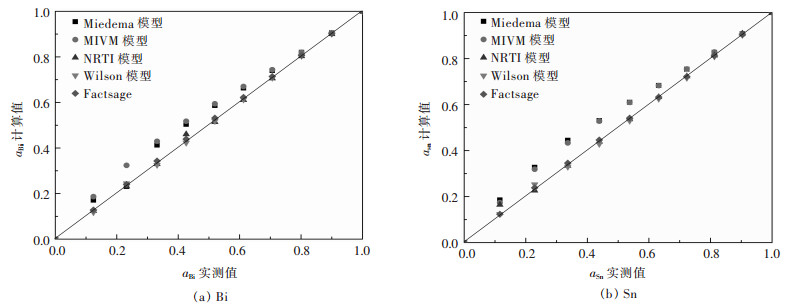图 2 Bi-Sn二元合金系活度a_Bi、a_Sn的实测值与其计算值的关系 Fig. 2 Relationship between measured activity a_Bi, a_Sn and calculated activity in full composition range of Bi-Sn binary melts by Miedema model, MIVM equation, NRTL equation, Wilson equation, FactSage, respectively

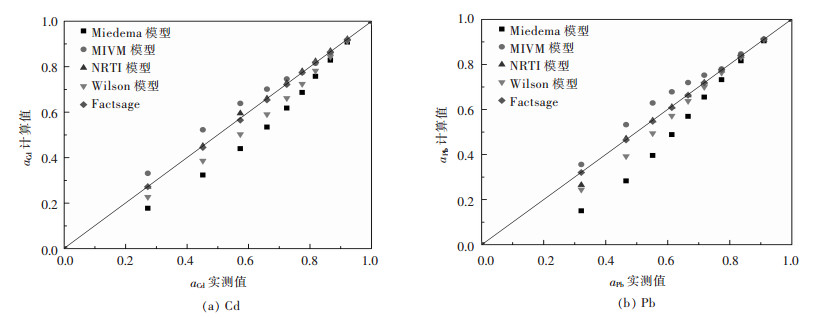图 3 Cd-Pb二元合金系活度a_Cd、a_Pb的实测值与其计算值的关系 Fig. 3 Relationship between measured activity a_Cd, a_Pb and calculated activity in full composition range of Cd-Pb binary melts by Miedema model, MIVM equation, NRTL equation, Wilson equation, FactSage, respectively

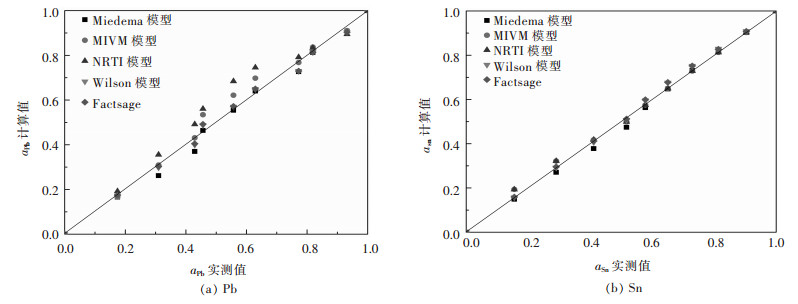图 4 Pb-Sn二元合金系活度a_Pb、a_Sn的实测值与其计算值的关系 Fig. 4 Relationship between measured activity a_Pb, a_Sn and calculated activity in full composition range of Pb-Sn binary melts by Miedema model, MIVM equation, NRTL equation, Wilson equation, FactSage, respectively

从图 1（a）可见，Bi-Pb二元合金系中Miedema模型计算的活度值a_Bi与实测值误差较大，而MIVM模型、NRTL模型、Wilson模型及FactSage热力学软件计算结果均吻合较好；图 1（b）中则可见Miedema模型、MIVM模型、Wilson模型活度计算值aPb与实测值比较出现较大误差.综合比较分析对于Bi-Pb二元合金系而言，NRTL模型和FactSage计算的结果较吻合. 图 2中可见，在Bi-Sn二元合金系全浓度范围内，NRTL模型、Wilson模型和FactSage计算的活度值与实测值吻合较好，而Miedema模型与MIVM模型在活度a_Bi>0.8时其计算值与实测值吻合较好.从图 3中可见，对Cd-Pb二元合金系NRTL模型与FactSage在全浓度范围内预测值与实测值吻合较好，其余模型只在活度值a_Bi>0.9时其预测值与实测值吻合较好.从图 4（a）中可见，Pb-Sn二元合金系中Wilson模型和FactSage活度预测值与实测值吻合较好，其他模型在活度值在0.2 < a_Bi < 0.8范围内误差较大，而组元Sn的活度aSn在全浓度范围内均吻合较好.

综上所述，对于上述4个二元合金系中任意体系和同一体系中的不同组元而言，Miedema模型、MIVM模型、NRTL模型和Wilson模型活度的预测值都不完全能够很好地与实测值相吻合，这可能是由于Miedema、MIVM、NRTL和Wilson模型计算不同体系活度的效果不同，每种模型都有其适用的体系.而由FactSage热力学软件得到的活度值均能与实测值很好地吻合.所以文中利用该软件计算上述4个二元合金系在不同温度下的活度. 表 1~表 4为FactSage计算得到的不同温度条件下各体系全浓度范围内活度值.

表1 Bi-Pb二元合金系的化学组成与活度计算值 Table 1 Chemical composition of Bi-Pb binary melts in full composition range at an interval of mole fraction x_Bi as 0.1, calculated activity a_Bi, aPb in 100 g Bi-Pb binary melts by FactSage in a temperature range from 700 to 1 000 K

编号	x_Bi	Bi-Pb二元系活度值
		700 K		800 K		900 K		1 000 K
		a_Bi	a_Pb	a_Bi	a_Pb	a_Bi	a_Pb	a_Bi	a_Sn
1	0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0
2	0.1	0.049 7	0.894 5	0.053 3	0.894 7	0.056 4	0.894 9	0.058 9	0.895 1
3	0.2	0.111 4	0.779 0	0.118 5	0.780 6	0.124 4	0.781 8	0.129 2	0.782 8
4	0.3	0.187 1	0.656 4	0.196 5	0.660 5	0.204 2	0.663 7	0.210 6	0.666 3
5	0.4	0.277 8	0.530 9	0.288 0	0.538 1	0.296 1	0.543 7	0.302 8	0.548 3
6	0.5	0.383 5	0.407 8	0.392 6	0.417 5	0.399 9	0.425 2	0.405 8	0.431 5
7	0.6	0.502 5	0.293 0	0.509 3	0.303 7	0.514 6	0.312 2	0.518 9	0.319 3
8	0.7	0.630 8	0.191 7	0.634 8	0.201 3	0.637 8	0.209 2	0.640 3	0.215 7
9	0.8	0.762 4	0.108 0	0.763 9	0.114 9	0.765 1	0.120 5	0.766 1	0.125 2
10	0.9	0.888 8	0.044 1	0.889 1	0.047 3	0.889 2	0.050 0	0.889 4	0.052 3
11	1.0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0

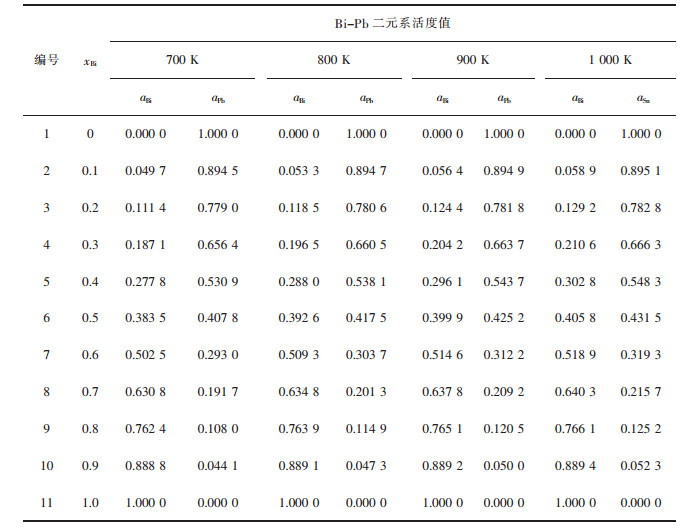点击放大

表2 Bi-Sn二元合金系的化学组成与活度计算值 Table 2 Chemical composition of Bi-Sn binary melts in full composition range at an interval of mole fraction x_Bi as 0.1, calculated activity a_Bi, a_Sn in 100 g Bi-Sn binary melts by FactSage in a temperature range from 600 to 900 K

编号	x_Bi	Bi-Sn二元系活度值
		600 K		700 K		800 K		9 000 K
		a_Bi	a_Sn	a_Bi	a_Sn	a_Bi	a_Sn	a_Bi	a_Sn
1	0.0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0
2	0.1	0.127 8	0.903 4	0.126 1	0.903 2	0.124 9	0.903 0	0.123 9	0.902 9
3	0.2	0.240 5	0.811 6	0.238 2	0.810 9	0.236 5	0.810 4	0.235 2	0.810 1
4	0.3	0.343 0	0.722 1	0.340 7	0.720 9	0.339 0	0.719 9	0.337 7	0.719 2
5	0.4	0.439 1	0.632 7	0.437 1	0.630 8	0.435 6	0.629 4	0.434 4	0.628 4
6	0.5	0.531 5	0.541 2	0.530 0	0.538 9	0.528 8	0.537 2	0.528 0	0.535 8
7	0.6	0.622 5	0.446 0	0.621 4	0.443 4	0.620 7	0.441 5	0.620 1	0.440 0
8	0.7	0.713 7	0.345 5	0.713 1	0.342 9	0.712 7	0.341 1	0.712 3	0.339 6
9	0.8	0.806 5	0.238 2	0.806 2	0.236 2	0.806 0	0.234 6	0.805 8	0.233 4
10	0.9	0.901 7	0.123 3	0.901 6	0.122 1	0.901 6	0.121 1	0.901 5	0.120 4
11	1.0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0

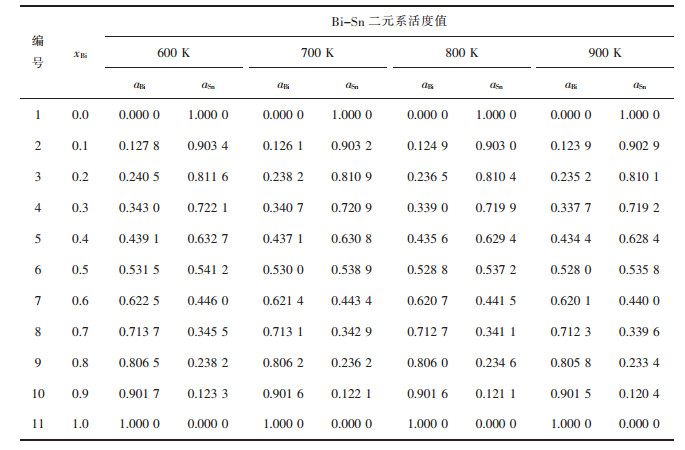点击放大

表3 Cd-Pb二元合金系的化学组成与活度计算值 Table 3 Chemical composition of Cd-Pb binary melts in full composition range at an interval of mole fraction x_Cd as 0.1, calculated activity a_Cd, a_Pb in 100 g Cd-Pb binary melts by FactSage in a temperature range from 773 to 1 073 K

编号	x_Cd	Cd-Pb二元系活度值
		773 K		873 K		973 K		1 073 K
		a_Cd	a_Pb	a_Cd	a_Pb	a_Cd	a_Pb	a_Cd	a_Pb
1	0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0
2	0.1	0.272 4	0.912 0	0.236 3	0.911 4	0.211 0	0.910 9	0.192 4	0.910 5
3	0.2	0.444 8	0.840 0	0.393 7	0.836 3	0.357 3	0.833 4	0.330 2	0.831 1
4	0.3	0.565 1	0.776 7	0.512 4	0.767 1	0.474 1	0.759 6	0.445 0	0.753 5
5	0.4	0.653 9	0.718 6	0.606 7	0.701 0	0.571 6	0.687 3	0.544 5	0.676 4
6	0.5	0.721 4	0.663 5	0.682 3	0.637 1	0.652 7	0.616 9	0.629 7	0.600 9
7	0.6	0.774 5	0.608 4	0.743 8	0.573 4	0.720 4	0.546 9	0.701 9	0.526 3
8	0.7	0.819 6	0.547 4	0.797 4	0.503 6	0.780 1	0.471 4	0.766 3	0.446 7
9	0.8	0.864 6	0.464 8	0.851 0	0.412 7	0.840 3	0.375 5	0.831 7	0.347 8
10	0.9	0.919 7	0.320 3	0.914 7	0.267 5	0.910 8	0.231 8	0.907 7	0.206 3
11	1.0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0

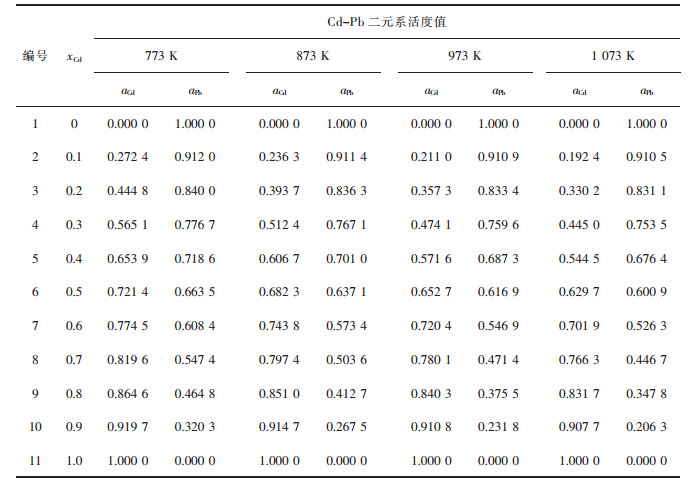点击放大

表4 Pb-Sn二元合金系的化学组成与其活度计算值 Table 4 Chemical composition of Pb-Sn binary melts in full composition range at an interval of mole fraction x_Pb as 0.1, calculated activity a_Pb, a_Sn in 100 g Pb-Sn binary melts by FactSage in a temperature range from 1 050 to 1 350 K

编号	x_Pb	Pb-Sn二元系活度值
		1 050 K		1 150 K		1 250 K		1 350 K
		a_Pb	a_Sn	a_Pb	a_Sn	a_Pb	a_Sn	a_Pb	a_Sn
1	0.0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0
2	0.1	0.174 1	0.907 9	0.166 2	0.907 5	0.159 9	0.907 2	0.154 7	0.906 9
3	0.2	0.302 7	0.827 1	0.291 2	0.825 6	0.282 0	0.824 4	0.274 3	0.823 3
4	0.3	0.404 6	0.751 9	0.392 2	0.748 7	0.382 1	0.746 0	0.373 7	0.743 7
5	0.4	0.491 7	0.677 4	0.480 1	0.671 9	0.470 5	0.667 3	0.462 5	0.663 5
6	0.5	0.571 8	0.598 8	0.561 9	0.590 8	0.553 7	0.584 1	0.546 9	0.578 5
7	0.6	0.649 9	0.511 7	0.642 4	0.501 3	0.636 1	0.492 8	0.630 9	0.485 6
8	0.7	0.729 8	0.412 0	0.724 8	0.400 0	0.720 6	0.390 2	0.717 1	0.382 1
9	0.8	0.813 7	0.295 6	0.811 2	0.283 9	0.809 0	0.274 3	0.807 2	0.266 5
10	0.9	0.903 5	0.159 1	0.902 8	0.150 8	0.902 1	0.144 1	0.901 6	0.138 7
11	1.0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0

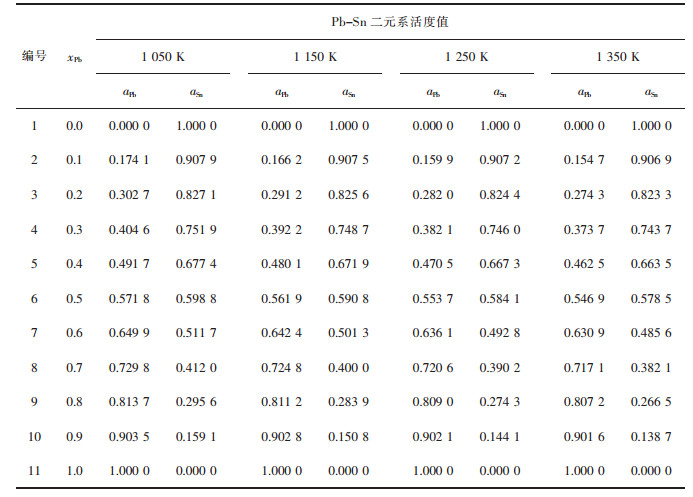点击放大

2 Bi-Pb二元系熔体中结构单元质量作用浓度的热力学模型

从Bi-Pb^[17]、Bi-Sn^[18]、Cd-Pb^[19]、Pb-Sn^[20]二元合金系相图可以看出，只有Bi-Pb二元合金系在一定温度下生成金属间化合物BiPb₃.当温度高于460 K时，化合物BiPb₃发生分解，在液相中化合物以何种分子存在仍需进一步分析.文中利用原子-分子理论，建立计算Bi-Pb二元合金系熔体中结构单元的质量作用浓度的AMCT-Ni模型，并得到生成化合物分子反应的标准生成吉布斯自由能.

2.1 模型假设条件

1）在冶金温度下，Bi-Pb二元系金属熔体中存在的结构单元包括：原子Bi和Pb；简单分子BiPb；

2）在Bi-Pb二元系熔体中，原子和分子各占一个结构单元；

3）在Bi-Pb二元系熔体中，原子Bi与Pb均参与形成简单分子BiPb的反应；

4）形成简单分子BiPb的反应存在动态平衡；

$ {\rm{Bi}} + {\rm{Pb}} = {\rm{BiPb}} $

(1)

5）在Bi-Pb二元系熔体中的结构单元在全浓度范围内具有连续性；

6）形成简单分子BiPb的化学反应满足质量作用定律.例如，K_ci^⊖＝N_BiPb/N_BiN_Pb.

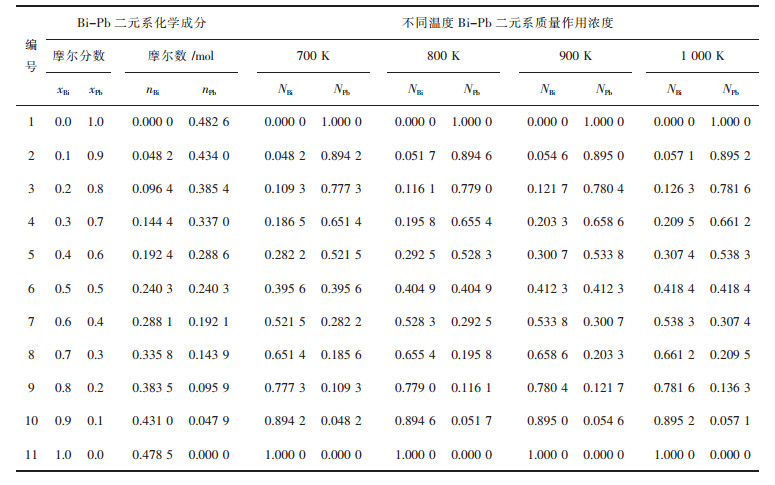
2.2 Bi-Pb二元系熔体中结构单元的质量作用浓度

以100 g Bi-Pb熔体作为研究对象，首先计算700 K、800 K、900 K、1 000 K下反应（1）全浓度范围内平衡常数的平均值分别为K₁=1.334 4、K₂=1.159 6、K₃=1.031 4、K₄=0.932 8，再由表 5计算得到的不同温度条件下全浓度范围内活度，可以得到Bi-Pb二元合金系中各结构单元的质量作用浓度，计算结果如表 5所列.

表5 100 g Bi-Pb二元系熔体的化学组成及其质量作用浓度 Table 5 Chemical composition of Bi-Pb binary melts in full composition range at an interval of mole fraction x_Bi as 0.1, calculated mass action concentration N_Bi, N_Pb in 100 g Bi-Pb binary melts based on the AMCT in a temperature range from 700 to 1 000 K

编号	Bi-Pb二元系化学成分				不同温度Bi-Pb二元系质量作用浓度
	摩尔分数		摩尔数/mol		700 K		800 K		900 K		1 000 K
	x_Bi	x_Pb	n_Bi	n_Pb	N_Bi	N_Pb	N_Bi	N_Pb	N_Bi	N_Pb	N_Bi	N_Pb
1	0.0	1.0	0.000 0	0.482 6	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0
2	0.1	0.9	0.048 2	0.434 0	0.048 2	0.894 2	0.051 7	0.894 6	0.054 6	0.895 0	0.057 1	0.895 2
3	0.2	0.8	0.096 4	0.385 4	0.109 3	0.777 3	0.116 1	0.779 0	0.121 7	0.780 4	0.126 3	0.781 6
4	0.3	0.7	0.144 4	0.337 0	0.186 5	0.651 4	0.195 8	0.655 4	0.203 3	0.658 6	0.209 5	0.661 2
5	0.4	0.6	0.192 4	0.288 6	0.282 2	0.521 5	0.292 5	0.528 3	0.300 7	0.533 8	0.307 4	0.538 3
6	0.5	0.5	0.240 3	0.240 3	0.395 6	0.395 6	0.404 9	0.404 9	0.412 3	0.412 3	0.418 4	0.418 4
7	0.6	0.4	0.288 1	0.192 1	0.521 5	0.282 2	0.528 3	0.292 5	0.533 8	0.300 7	0.538 3	0.307 4
8	0.7	0.3	0.335 8	0.143 9	0.651 4	0.185 6	0.655 4	0.195 8	0.658 6	0.203 3	0.661 2	0.209 5
9	0.8	0.2	0.383 5	0.095 9	0.777 3	0.109 3	0.779 0	0.116 1	0.780 4	0.121 7	0.781 6	0.136 3
10	0.9	0.1	0.431 0	0.047 9	0.894 2	0.048 2	0.894 6	0.051 7	0.895 0	0.054 6	0.895 2	0.057 1
11	1.0	0.0	0.478 5	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0	1.000 0	0.000 0

点击放大

图 5所示为Bi-Pb二元系熔体中结构单元Bi、Pb的质量作用浓度与其活度之间的关系，可以看出二者高度吻合.所以，可以使用基于原子-分子理论的Bi-Pb二元系熔体中结构单元Bi、Pb的质量作用浓度N_Bi、N_Pb来替代a_Bi、a_Pb.

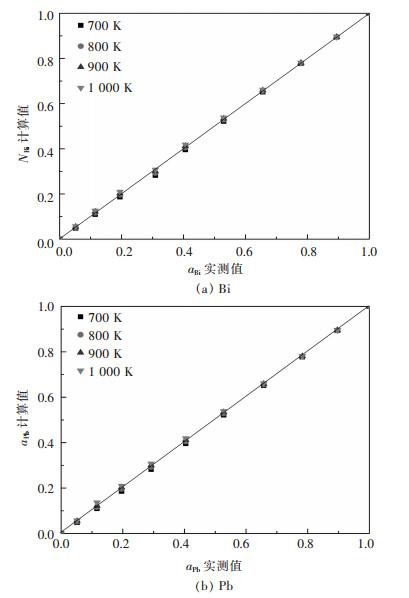图 5 Bi-Pb二元合金系全浓度范围内活度a_Bi、a_Pb的实测值与其质量作用浓度的关系 Fig. 5 Relationship between measured activity a_Pb, a_Sn and calculated mass action concentration N_Bi、N_Pb in full composition range of Bi-Pb binary melts at temperatures of 700 K, 800 K, 900 K, 1 000 K, respectively

2.3 计算结果分析

图 6所示为不同温度条件下，组元Bi的摩尔分数x_Bi与Bi-Pb二元合金系中结构单元Bi、Pb、BiPb的质量作用浓度N_Bi、N_Pb、N_BiPb及总平衡摩尔数∑η_i的关系.可以看出，结构单元Bi、Pb的质量作用浓度N_Bi、N_Pb相对Raoult定律呈负偏差；BiPb的质量作用浓度N_BiPb随着组元Bi的摩尔分数的增加先增加后减小，在x_Bi=0.5时达到最大，并且随着温度的增加其最大值逐渐减小.这可能是因为组元Bi的含量越小或越大均不利于化合物BiPb的生成，且温度升高促进了化合物BiPb的分解反应.

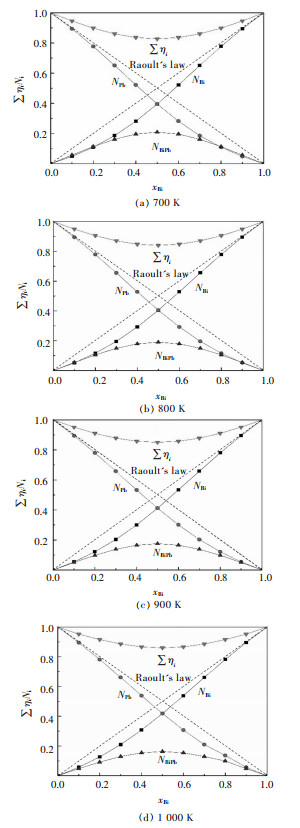图 6 Bi-Pb二元系熔体中Bi的摩尔分数x_Bi与各结构单元质量作用浓度之间的关系 Fig. 6 Relationship between mole fraction x_Bi of Bi and calculated mass action concentration of structural units as BiPb in full composition range of Bi-Pb binary melts in a temperature range from 700 to 1 000 K

图 7所示为Bi-Pb二元系熔体中形成化合物分子BiPb化学反应的标准摩尔吉布斯自由能ΔG_BiPb^⊖的表达式，同时可见拟合表达式的确定系数接近于1，说明该表达式具有很好的准确性，同时也证明上述所假设的该二元系合金系结构单元是正确的.

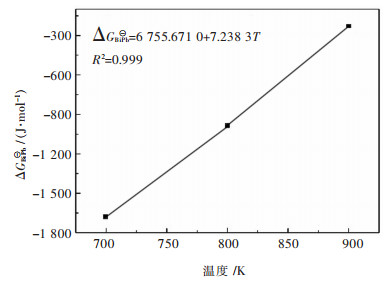图 7 Bi-Pb二元系熔体中形成分子BiPb化学反应的标准摩尔吉布斯自由能变化拟合关系 Fig. 7 Standard molar Gibbs free energy change of reaction for forming associated molecules as BiPb in Bi-Pb binary melts at temperatures of 700, 800, and 900 K, by simple linear fitting method

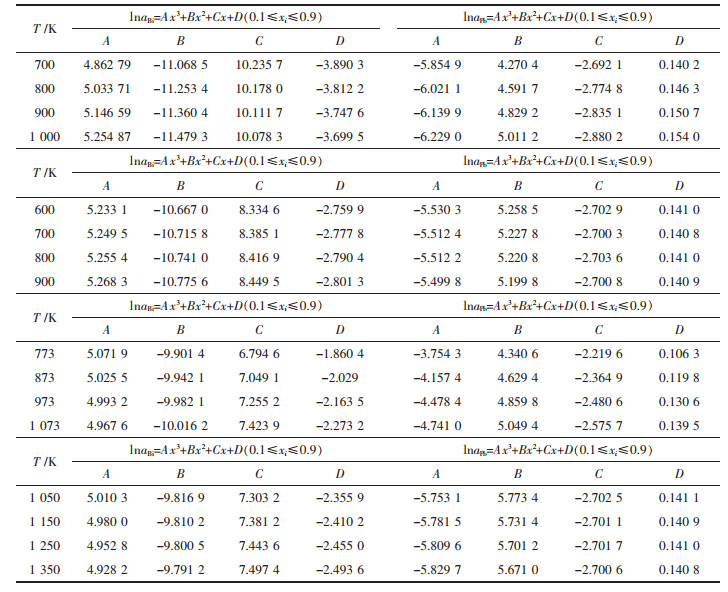
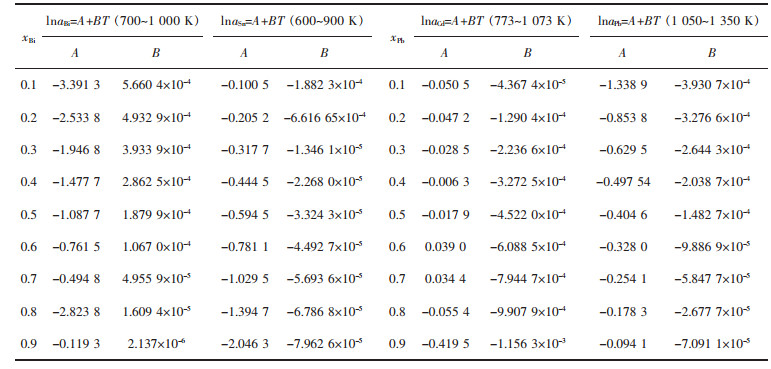
表 6和表 7分别列出了上述各体系活度的对数ln_{a_i}组成与温度的关系：ln_{a_i}=Ax³+Bx²+Cx+D（0.1≤x_i≤0.9），ln_{a_i}=A+BT.

表6 Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn二元合金系活度a_i的对数形式lna_i与组成x_i的关系 Table 6 Relationship between mole fraction x_i in full composition range at an interval as 0.1 and activity in logarithmic form lna_i in Bi-Pb binary system, Bi-Sn binary system, Cd-Pb binary system, Pb-Sn binary system, respectively

T/K	Ina_Bi=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Pb=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Bi=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Pb=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Bi=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Pb=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Bi=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)				Ina_Pb=Ax³+Bx²+Cx+D(0.1≤x_i≤0.9)
T/K	A	B	C	D	A	B	C	D	A	B	C	D	A	B	C	D	A	B	C	D	A	B	C	D	A	B	C	D	A	B	C	D
700	4.862 79	-11.068 5	10.235 7	-3.890 3	-5.854 9	4.270 4	-2.692 1	0.140 2	5.233 1	-10.667 0	8.334 6	-2.759 9	-5.530 3	5.258 5	-2.702 9	0.141 0	5.071 9	-9.901 4	6.794 6	-1.860 4	-3.754 3	4.340 6	-2.219 6	0.106 3	5.010 3	-9.816 9	7.303 2	-2.355 9	-5.753 1	5.773 4	-2.702 5	0.141 1
800	5.033 71	-11.253 4	10.178 0	-3.812 2	-6.021 1	4.591 7	-2.774 8	0.146 3	5.249 5	-10.715 8	8.385 1	-2.777 8	-5.512 4	5.227 8	-2.700 3	0.140 8	5.025 5	-9.942 1	7.049 1	-2.029	-4.157 4	4.629 4	-2.364 9	0.119 8	4.980 0	-9.810 2	7.381 2	-2.410 2	-5.781 5	5.731 4	-2.701 1	0.140 9
900	5.146 59	-11.360 4	10.111 7	-3.747 6	-6.139 9	4.829 2	-2.835 1	0.150 7	5.255 4	-10.741 0	8.416 9	-2.790 4	-5.512 2	5.220 8	-2.703 6	0.141 0	4.993 2	-9.982 1	7.255 2	-2.163 5	-4.478 4	4.859 8	-2.480 6	0.130 6	4.952 8	-9.800 5	7.443 6	-2.455 0	-5.809 6	5.701 2	-2.701 7	0.141 0
1 000	5.254 87	-11.479 3	10.078 3	-3.699 5	-6.229 0	5.011 2	-2.880 2	0.154 0	5.268 3	-10.775 6	8.449 5	-2.801 3	-5.499 8	5.199 8	-2.700 8	0.140 9	4.967 6	-10.016 2	7.423 9	-2.273 2	-4.741 0	5.049 4	-2.575 7	0.139 5	4.928 2	-9.791 2	7.497 4	-2.493 6	-5.829 7	5.671 0	-2.700 6	0.140 8

点击放大

表7 Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn二元合金系活度a_i的对数形式lna_i与组成x_i的关系 Table 7 Relationship between temperature T and activity in logarithmic form lna_i in Bi-Pb binary system, Bi-Sn binary system, Cd-Pb binary system, Pb-Sn binary system, respectively

x_Bi	Ina_Bi=A+BT(700~1 000 K)		Ina_Sn=A+BT(600~900 K)		x_Pb	Ina_Cd=A+BT(773~1 073 K)		Ina_Pb=A+BT(1 050~1 350 K)
x_Bi	A	B	A	B	x_Pb	A	B	A	B
0.1	-3.391 3	5.660 4×10^-4	-0.100 5	-1.882 3×10^-4	0.1	-0.050 5	-4.367 4×10^-5	-1.338 9	-3.930 7×10^-4
0.2	-2.533 8	4.932 9×10^-4	-0.205 2	-6.616 65×10^-4	0.2	-0.047 2	-1.290 4×10^-4	-0.853 8	-3.276 6×10^-4
0.3	-1.946 8	3.933 9×10^-4	-0.317 7	-1.346 l×10^-5	0.3	-0.028 5	-2.236 6×10^-4	-0.629 5	-2.644 3×10^-4
0.4	-1.477 7	2.862 5×10^-4	-0.444 5	-2.268 0×10^-5	0.4	-0.006 3	-3.272 5×10^-4	-0.497 54	-2.038 7×10^-4
0.5	-1.087 7	1.879 9×10^-4	-0.594 5	-3.324 3×10^-5	0.5	-0.017 9	-4.522 0×10^-4	-0.404 6	-1.482 7×10^-4
0.6	-0.761 5	1.067 0×10^-4	-0.781 1	-4.492 7×10^-5	0.6	0.039 0	-6.088 5×10^-4	-0.328 0	-9.886 9×10^-5
0.7	-0.494 8	4.955 9×10^-5	-1.029 5	-5.693 6×10^-5	0.7	0.034 4	-7.944 7×10^-4	-0.254 1	-5.847 7×10^-5
0.8	-2.823 8	1.609 4×10^-5	-1.394 7	-6.786 8×10^-5	0.8	-0.055 4	-9.907 9×10^-4	-0.178 3	-2.677 7×10^-5
0.9	-0.119 3	2.137×10^-6	-2.046 3	-7.962 6×10^-5	0.9	-0.419 5	-1.156 3×10^-3	-0.094 1	-7.091 1×10^-5

点击放大

3 结论

1）FactSage适用于Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn二元合金系，计算得到的活度值与实验值吻合较好，并使用FactSage计算上述4个合金二元系在不同温度下的活度.

2）从Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn二元合金系相图看出，只有Bi-Pb二元合金系生成金属间化合物BiPb₃，当温度高于460 K时该化合物分解生成BiPb.组元Bi的摩尔分数x_Bi=0.5时，Bi-Pb二元合金系中结构单元BiPb的质量作用浓度NBiPb达到最大，但随温度的升高逐渐降低.

3）根据原子-分子理论分别得到在700 K、800 K、900 K下，生成BiPb分子的化学反应平衡常数为K₁=1.334 4、K₂=1.159 6、K₃=1.031 4，通过拟合得到其标准吉布斯自由能的表达式ΔG_BiPb^⊖=-6 755.67+7.24 T（J/mol），同时给出了Bi-Pb、Bi-Sn、Cd-Pb、Pb-Sn二元合金系中各组元活度与组成、温度的关系式.

参考文献

[1]	许帅, 宋冰宜, 蒋文龙, 等. 几种热力学模型应用于二元合金中各组元活度计算的研究[J]. 真空科学与技术学报, 2015, 35(8): 919–925.
[2]	乐启炽, 张新建, 崔建忠, 等. 金属合金溶液热力学模型研究进展[J]. 金属学报, 2003, 39(1): 35–42.
[3]	SHIBAEV S S, KRASOVSKII P V, GRIGOROVITCH K V. Solubility of oxygen in iron-silicon melts in equilibrium with silica at 1873 K[J]. ISIJ international, 2005, 45(9): 1243–1247. DOI: 10.2355/isijinternational.45.1243.
[4]	车冠全, 裘利言, 郑国康. 凝固点降低法测二元稀溶液的活度系数[J]. 兰州大学学报, 1984(增刊2): 182–188.
[5]	陶俊, 陶然, 闫柏军. 钒在铁液中活度系数的实验研究[J]. 有色金属科学与工程, 2016, 7(1): 11–14.
[6]	陶俊, 陶然, 闫柏军. 钒在铜液中活度系数的实验研究[J]. 有色金属科学与工程, 2015, 6(2): 27–31.
[7]	CHIPMAN J, BASCHWIT R. Activity of silicon in liquid Fe-Calloys[J]. Transactions of the Metallurgical Society of America, 1963, 227(2): 473.
[8]	FRUEHAN R J. Activities in liquid Fe-Al-O and Fe-Ti-O alloys[J]. Metallurgical Transactions, 1970, 1(12): 3403–3410.
[9]	郭汉杰. 冶金物理化学[M]. .
[10]	DARKEN L S. Thermodynamics of binary metallic solutions[J]. Aime Met Soc Trans, 1967, 239(1): 80–89.
[11]	WILSON G M. Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing[J]. Journal of the American Chemical Society, 1964, 86(2): 127–130. DOI: 10.1021/ja01056a002.
[12]	RENON H, PRAUSNITZ J M. Local compositions in thermodynamic excess functions for liquid mixtures[J]. AIChE Journal, 1968, 14(1): 135–144. DOI: 10.1002/(ISSN)1547-5905.
[13]	MIEDEMA A R, DE CHATEL P F, DE BOER F R. Cohesion in alloys-fundamentals of a semi-empirical model[J]. Physica B+C, 1980, 100(1): 1–28.
[14]	张鉴. 冶金熔体和溶液的计算热力学[M]. 北京: 冶金工业出版社, 2007.
[15]	BALE C W, ERIKSSON G. Metallurgical thermochemical databases-a review[J]. Canadian Metallurgical Quarterly, 1990, 29(2): 105–132. DOI: 10.1179/cmq.1990.29.2.105.
[16]	TAO D P. A new model of thermodynamics of liquid mixtures and its application to liquid alloys[J]. Thermochimica Acta, 2000, 363(1): 105–113.
[17]	YOON S W, LEE H M. A thermodynamic study of phase equilibria in the Sn-Bi-Pb solder system[J]. Calphad, 1998, 22(2): 167–178. DOI: 10.1016/S0364-5916(98)00022-4.
[18]	OHTANI H, ISHIDA K. A thermodynamic study of the phase equilibria in the Bi-Sn-Sb system[J]. Journal of Electronic Materials, 1994, 23(8): 747–755. DOI: 10.1007/BF02651369.
[19]	DUTKIEWICZ J, MOSER Z, ZAKULSKI W. The Cd-Pb (Cadmium-Lead) system[J]. Bulletin of Alloy Phase Diagrams, 1988, 9(6): 694–701. DOI: 10.1007/BF02883171.
[20]	PRESCOTT P J, INCROPERA F P. Numerical simulation of a solidifying Pb-Sn alloy: The effects of cooling rate on thermosolutal convection and macrosegregation[J]. Metallurgical Transactions B, 1991, 22(4): 529–540. DOI: 10.1007/BF02654292.