| 南方离子型稀土一维水平入渗规律试验研究 |
b. 江西理工大学, 资源与环境工程学院,江西 赣州 341000
b. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
南方离子吸附型稀土矿是我国最早发现的一类独特且富含中重稀土的矿产资源,以离子态赋存,目前多采用原地浸开采工艺[1-2].原地浸不需要剥离表土和开挖矿体,直接在山体表面布置注液井网,注入浸矿液到拟开采区域的稀土层,铵根离子与稀土离子发生交换反应,浸矿母液通过渗透作用流出山体汇集到母液池.浸矿液在稀土中入渗情况直接影响稀土资源的利用率与回收率[3].
入渗是外来水分进入土壤的过程,灌溉、降雨、污染物迁移和溶浸采矿等都涉及到土壤的入渗[4-7].王全九等[8]研究土壤初始含水量对微碱水入渗特征的影响;牛文全等[9]采用微润灌溉方式研究不同矿化度下土壤的入渗特征;王观石等[10]建立了非达西渗流条件下的单孔注液强度计算模型;罗嗣海等[11-12]探讨了浸矿对离子型稀土矿颗粒粒径和强度的影响规律;吴爱祥等[13]探讨了矿物颗粒表面结合水的形成机理及其对溶浸液渗流规律的影响.离子型稀土矿具有黏土矿物性质,离子交换反应属于2类离子的双向运动[14-15],有别于盐水灌溉时离子的单向迁移;原地浸的注液井有一定的注水高度,即存在一定的水头压力,也有别于农业灌溉时的点源入渗,更有别于大气降雨的土壤入渗.
以离子型稀土原地浸开采为工程背景,基于自制试验装置[16],在前期一维垂直入渗试验的基础上[17-18],进行一维水平入渗室内试验,探究离子型稀土溶浸液入渗规律及最大粒径的影响,试验研究结果为进一步研究溶浸液三维入渗规律奠定了基础,有助于完善原地浸矿工艺理论体系,为原地浸矿工程实践提供参考数据.
1 试验装置和材料 1.1 试验装置一维水平入渗装置由主管、注水管、测压管、马氏瓶、溢水管、渗水管等组成,如图 1所示.主管为外径为50 mm、长度为2 000 mm的有机玻璃管,主管表面贴有精度为1 mm的刻度尺,用于读取湿润锋长度;压力管的高度为400 mm,压力水头为350 mm,压力管的水平部分和主管连接处用滤布隔开,防止土颗粒进入压力管造成堵塞;测压管外径为20 mm、高度为350 mm,垂直安装在主管上,间距为300 mm,端头测压管距主管两端为400 mm,测压管面贴有精度为1 mm的刻度尺,用于读取压力水头高度;溢水管用于保持350 mm水头高度,渗水管用于测量析出的渗水量;入渗溶液选用原地浸矿工艺中使用的3 %硫酸铵溶液.
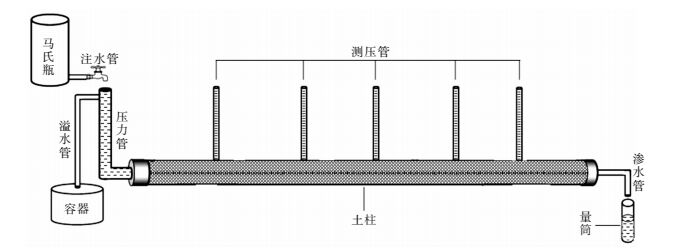 |
| 图 1 -维水平入渗装置示意 Fig. 1 One-dimensional horizontal infiltration test device |
1.2 试验土样
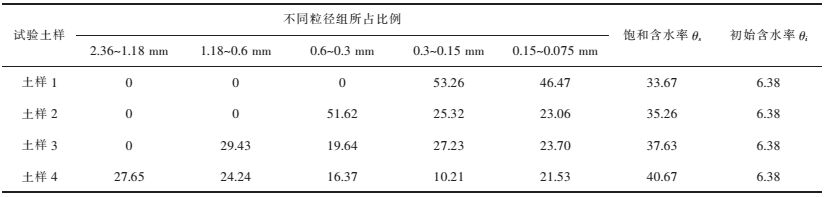
稀土试样取自赣南寻乌县某稀土矿山,在室内放置若干天,风化完全.试验前,将块度较大矿土进行简单地碾压,为了研究粒径对入渗的影响,根据原矿颗粒级配,依次从小到大选取试验粒径范围,然后进行筛分,按最大粒径0.3 mm、0.6 mm、1.18 mm、2.36 mm把土样分为4组.土样物理参数见表 1.
| 表1 土样物理参数/% Table 1 Physical indexes of soil samples /% |
 |
| 点击放大 |
2 结果和分析 2.1 累积入渗长度变化规律
一维水平入渗过程中,浸矿液在基质吸力和水头压力的作用下进入土体并在土内进行水平运动.图 2所示为3 %硫酸铵溶液下的湿润锋随时间的变化规律,可以看出,随着入渗时间增加,湿润的稀土体积越来越大,湿润锋累计入渗长度随之增长,不同粒径级配的稀土湿润锋运移规律基本相同.对于最大粒径不同的稀土湿润锋推进的速度略有不同.
 |
| 图 2 累计入渗深度随时间的变化关系 Fig. 2 Relationship between cumulative infiltration depth and time |
2.2 湿润锋运移速率变化规律
4组稀土土样湿润锋运移速度随时间的变化规律趋势相同,图 3所示为土样1的湿润锋运移速率随时间变化关系.在入渗前期,湿润锋运移速率快速下降,随着入渗时间增加,湿润锋运移速率逐渐趋于一个稳定值.土样1至土样4对应的稳定湿润锋运移速率分别为:0.005 2 cm/min、0.006 0 cm/min、0.006 2 cm/min、0.007 4 cm/min,可以看出:在一维水平入渗中,土样的最大粒径对入渗的湿润锋运移速率有一定影响,随着最大粒径的增大,稳定湿润锋运移速率也会相应增大.
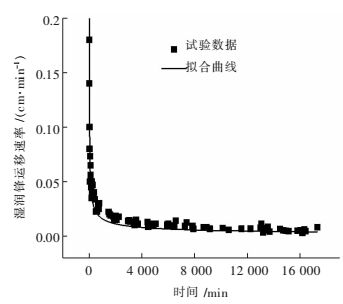 |
| 图 3 湿润锋运移速率随时间的变化关系 Fig. 3 Relationship between wetting front migration rate and time |
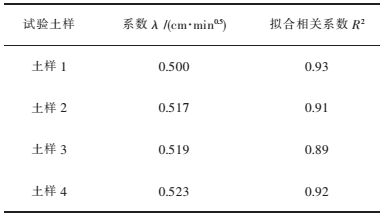
湿润锋运移速率与时间的变化规律符合幂函数关系v=λ·t-0.5,λ为拟合参数.利用该函数拟合湿润锋运移速率随时间变化的试验数据,拟合结果如表 2所示,λ在0.5~0.523之间,且随着最大粒径的增大而增大,说明λ可表示粒径的大小对入渗的影响情况.
| 表2 湿润锋运移速率与时间关系的拟合参数 Table 2 Fitting parameters of wetting front migration velocity and time |
 |
| 点击放大 |
2.3 入渗率变化规律
入渗率是单位时间内通过单位横截面积的水的通量,反映了土壤的入渗能力.土壤对水的渗透能力一般用入渗率或者累积入渗率来衡量.根据Green-Ampt入渗模型[19],假定土壤入渗时存在明显的湿润锋面,湿润锋面将土壤分为饱和区和未湿润区.湿润锋后面为饱和区,土壤含水率为饱和含水率θs,导水率为饱和导水率,湿润锋前面为未湿润区,土壤含水率为初始含水率θi.分析水平入渗过程中,假设湿润锋推进的方向为x轴方向,湿润锋位置为xf.水平土柱在试验过程中,不考虑重力势影响,只存在基质吸力sf和压力水头的压力势.由达西定律可知,入渗率为:
| $i = {k_s}\frac{{{h_0} + {s_f}}}{{{x_f}}}$ | (1) |
依据水量平衡原理,入渗过程中马氏瓶减小的水量与入渗过程中渗入土体内的水量是相等的,通过累计入渗量和湿润锋关系可以得出:
| $I = \left( {{\theta _s} - {\theta _i}} \right) \cdot {x_f}$ | (2) |
对入渗量求导,可得:
| $i = \frac{{{\rm{d}}I}}{{{\rm{d}}t}} = \left( {{\theta _s} - {\theta _i}} \right)\frac{{{\rm{d}}{x_f}}}{{{\rm{d}}t}}$ | (3) |
根据公式 (3) 可以求出入渗率,土样1入渗率随时间变化如图 4所示.可以看出,入渗率的大小随着入渗时间发生变化,不同最大粒径下的水平入渗率随时间的变化趋势大致相同.初期入渗率大,随着入渗时间的增加,在入渗60 min之后,入渗率迅速下降;入渗1 500 min之后,入渗率逐渐趋于稳定,4种土样的稳定入渗率分别为0.001 2 cm/min、0.001 7 cm/min、0.002 0 cm/min、0.002 3 cm/min,入渗率随着最大粒径的增大而增大.
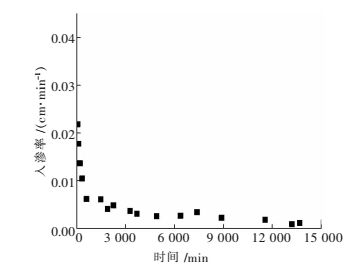 |
| 图 4 入渗率随时间的变化关系 Fig. 4 Relationship of infiltration rate with time |
2.4 饱和渗透系数
随着入渗的进行,测压管中逐渐有水头出现,图 5所示为土样1的测压管水头高度随时间变化曲线;随着入渗时间不断增长,水平试验装置末端开始析出水,图 6所示为累积析出水量和时间的变化关系.
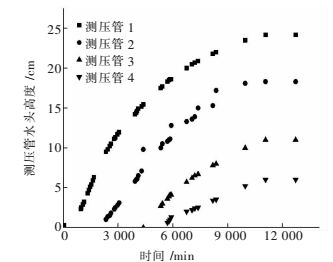 |
| 图 5 测压管水头高度随时间的变化关系 Fig. 5 Relationship between water head height of pressure measuring tube and time |
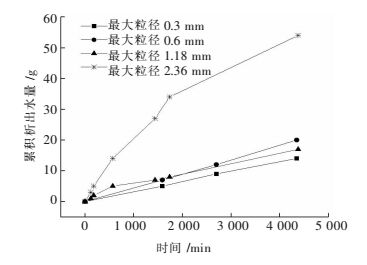 |
| 图 6 累积析出水量随时间的变化关系 Fig. 6 Relationship between accumulated outflow water and time |
由图 5可知,各测压管中水头高度上升规律趋势相同,水头出现初期,其上升速度快,随着入渗时间的增长,速度逐渐减小,最终测压管中水头高度趋于一个稳定值.同一土柱中各测压管水头高度随入渗长度的递增而递减.这是因为:水中任意一点的总势能包括压力势、基质势、重力势、溶质势和温度势,溶质势和温度势一般可忽略不计[20-21],水中任意两点间如存在水头差时就会发生渗流,水从能量高处流向能量低处.当水在压力势、基质势和重力势作用下流动时,由于总水头控制不变,即压力势恒定,但由于基质势作用和水与试验装置的器壁间的黏滞力作用所消耗的能量,故水头存在着能量损耗,导致该现象.由图 6可知,累积析出水量和时间呈直线关系,因为入渗过程中包含多个阶段,分别为非饱和入渗阶段、饱和非稳定阶段和饱和稳定阶段,由于渗水管单位时间内析出的水量大致相等,可判断装置末端有水析出时为第3阶段饱和稳定阶段,已经形成了稳定流.
根据饱和达西定律,有:
| $Q = k\frac{h}{L}At$ | (4) |
其中:Q为渗流量,k为饱和渗透系数,A为土柱的横截面积,h为水头差,L为渗径长度,t为入渗时间.
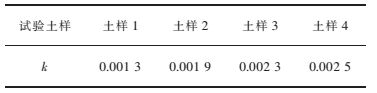
由式(4)可计算出饱和渗透系数k,如表 3所列.可以看出,随着最大粒径的增大,水平入渗的饱和渗透系数k逐渐增大.
| 表3 不同土样的饱和渗透系数值/(cm·min-1) Table 3 Value of saturated permeability coefficient |
 |
| 点击放大 |
3 结论
1) 4种不同粒径稀土样一维水平入渗的湿润锋累积入渗长度随时间的变化趋势一致.随着入渗时间的增加,湿润锋累积入渗深长呈现先快速增加,后缓慢发展趋势.
2) 湿润锋运移速率先达到最大值,后快速减小再趋于稳定;不同粒径的土样,对湿润锋运移速率影响不同.湿润锋运移速率与时间之间的关系符合幂函数关系,在一定粒径范围内,湿润锋运移速率随着最大粒径的增大而递增,其参数λ相应递增.
3) 通过试验计算得出水平饱和渗透系数,3 %硫酸铵溶液入渗到最大粒径0.3 mm、0.6 mm、1.18 mm、2.36 mm的土样中,饱和渗透系数分别为0.001 3 cm/min、0.001 9 cm/min、0.002 3 cm/min、0.002 5 cm/min.在一定粒径范围内,土样的最大粒径对饱和渗透系数有影响,随着最大粒径的增大水平饱和渗透系数也会增大.这也说明:粒径对入渗的影响,有必要在稀土矿山原地浸开采工程实践中予以考虑.
| [1] | 池汝安, 田君, 罗仙平, 等. 风化壳淋积型稀土矿的基础研究[J]. 有色金属科学与工程, 2012, 3(4): 1–13. |
| [2] | 田君, 唐学昆, 尹敬群, 等. 风化壳淋积型稀土矿浸取过程中基础理论研究现状[J]. 有色金属科学与工程, 2012, 3(4): 48–52. |
| [3] | 罗仙平, 翁存建, 徐晶, 等. 离子型稀土矿开发技术研究进展及发展方向[J]. 金属矿山, 2014, 43(6): 83–90. |
| [4] | 孙海燕, 李明思, 王振华, 等. 滴灌点源人渗湿润锋影响因子的研究[J]. 灌溉排水学报, 2004, 23(3): 14–16. |
| [5] | 荣冠, 张伟, 周创兵. 降雨入渗条件下边坡岩体饱和非饱和渗流计算[J]. 岩土力学, 2005, 26(10): 1545–1550. DOI: 10.3969/j.issn.1000-7598.2005.10.005. |
| [6] | 李华伟, 白冰, 王梦恕, 等. 渗透作用下多孔介质中循环浓度污染物的迁移过程研究[J]. 岩土力学, 2015, 36(5): 1306–1312. |
| [7] | 叶勇军, 丁德馨, 李广悦, 等. 堆浸铀矿堆液体饱和渗流规律的研究[J]. 岩土力学, 2013, 34(8): 2243–2248. |
| [8] | 王全九, 叶海燕, 史晓南, 等. 土壤初始含水量对微咸水入渗特征影响[J]. 水土保持学报, 2004, 2(1): 51–53. |
| [9] | 牛文全, 薛万来. 矿化度对微润灌土壤入渗特性的影响[J]. 农业机械学报, 2014, 4(4): 163–172. DOI: 10.6041/j.issn.1000-1298.2014.04.026. |
| [10] | 王观石, 邓旭, 胡世丽, 等. 非达西渗流条件下的单孔注液强度计算模型[J]. 矿冶工程, 2015, 35(6): 4–8. |
| [11] | 罗嗣海, 袁磊, 王观石, 等. 浸矿对离子型稀土矿强度影响的试验研究[J]. 有色金属科学与工程, 2013, 4(3): 58–61. |
| [12] | 王洪丁, 王观石, 邱高磊, 等. 离子型稀土矿体强度特性试验研究[J]. 中国矿业, 2016, 25(9): 136–140. |
| [13] | 吴爱祥, 尹升华, 李建锋. 离子型稀土矿原地溶浸溶浸液渗流规律的影响因素[J]. 中南大学学报 (自然科学版), 2005, 36(3): 506–510. |
| [14] | 李永绣, 周新木, 刘艳珠, 等. 离子吸附型稀土高效提取和分离技术进展[J]. 中国稀土学报, 2012, 30(3): 258–264. |
| [15] | 池汝安, 田君. 风化壳淋积型稀土矿评述[J]. 中国稀土学报, 2007, 25(6): 641–650. |
| [16] | 金解放, 常军然, 袁伟. 裸脚式稀土矿原地浸开采渗流模拟实验方法及装置: 中国, 201610073985. X[P], 2016-07-27. |
| [17] | 金解放, 邱灿, 陶伟, 等. 毛细上升渗透系数的确定及在离子型稀土毛细上升中的应用[J]. 有色金属科学与工程, 2015, 6(4): 104–110. |
| [18] | 金解放, 陶伟, 邱灿, 等. 离子型稀土一维垂直入渗规律及最大粒径的影响试验研究[J]. 有色金属科学与工程, 2015, 6(6): 125–131. |
| [19] | 韦昌富, 侯龙, 简文星. 非饱和土力学[M]. 北京: 高等教育出版社, 2012. |
| [20] | 李广信. 高等土力学[M]. 北京: 高等教育出版社, 2004. |
| [21] | 景卫华, 贾忠华, 罗纨. 总水势概念的定义、计算及应用条件[J]. 农业工程学报, 2008, 24(2): 27–32. |
 2017, Vol. 8
2017, Vol. 8


