| 基于模糊数学的矿区土壤重金属污染评价——以信丰稀土矿区为例 |
土壤重金属污染是一个复杂、模糊多变的体系,污染评价中存在着模糊性和渐变性的特点. 目前国内外常用于土壤重金属评价的方法有很多种,包括单因子污染指数法[1-2]、内梅罗指数法[3-4]、地累积指数法[5-6]、潜在生态危害指数法[7-8]等,这些传统的污染指数法在土壤重金属污染评价中得到广泛的应用,但难以描述土壤污染评价的模糊性和渐变性. 模糊评价法是一种研究和处理模糊现象的新型数学方法[9-11],广泛应用于空气污染、水污染和土壤污染等环境评价中[12-13]. 不同评价方法各有优缺点,评价方法主要是评价研究区土壤的污染程度,但很少有学者对多种评价方法进行对比分析. 鉴于土壤重金属污染评价中的模糊性和渐变性,文中以信丰4个稀土矿区为例,构建模糊数学污染评价模型,评价8种重金属元素Cu、Pb、Zn、Cd、As、Cr、Hg、Ni的污染情况,并与传统的污染指数对比分析,探讨模糊数学法在土壤重金属污染评价应用中的合理性.
1 模糊数学模型模糊评价法是以模糊数学为基础的一种综合评价方法[14-17],应用非常广泛,该方法应用于土壤重金属污染评价的一般步骤如下:
1) 构建评价因子集和评价集.评价因子集是参与评价的因子组成的模糊子集,即X={x1,x2,…,xn},xi为影响评价的第i个因子,评价集是评价对象的评估结果组成的集合,即V={v1,v2,…,vn},vi为评价的第i个评价等级.
2) 建立隶属度函数R. 确定每一个因子xi对评价集v的隶属程度,以rij表示,将所有单因子评价集组成的矩阵R称为模糊关系矩阵,公式如下:
| $R = \left[ {\matrix{ {{r_{11}}} & {{r_{12}}} & \cdots & {{r_{1m}}} \cr {{r_{21}}} & {{r_{22}}} & \cdots & {{r_{2m}}} \cr \vdots & \vdots & \vdots & \vdots \cr {{r_{n1}}} & {{r_{n2}}} & \cdots & {{r_{nm}}} \cr } } \right]$ |
当j=1时,隶属度函数为:
| ${{r}_{i1}}=\left\{ \begin{align} & 1,{{u}_{i}}\le {{S}_{i1}} \\ & \frac{{{S}_{i2}}-{{u}_{i}}}{{{S}_{i2}}-{{S}_{i1}}},{{S}_{i1}}<{{u}_{i}}<{{S}_{i2}} \\ & 0,{{u}_{i}}\ge {{S}_{i2}} \\ \end{align} \right.$ |
当1<j<m时,隶属度函数为:
| ${{r}_{i1}}=\left\{ \begin{align} & 0,{{u}_{i}}\le {{S}_{i,j+1}}或{{u}_{i}}\ge {{S}_{i,j+1}} \\ & \frac{{{u}_{i}}-{{S}_{i,j-1}}}{{{S}_{i,j+1}}-{{S}_{ij}}},{{S}_{i,j-1}}<{{u}_{i}}<{{S}_{ij}} \\ & \frac{{{S}_{i,j+1}}-{{u}_{i}}}{{{S}_{i,j+1}}-{{S}_{ij}}},{{S}_{i,j}}<{{u}_{i}}<{{S}_{i,j+1}} \\ & 1,{{u}_{i}}={{S}_{ij}} \\ \end{align} \right.1<j<m$ |
当j=m时,隶属度函数为:
| ${{r}_{im}}=\left\{ \begin{align} & 0,{{u}_{i}}\le {{S}_{i,m-1}} \\ & \frac{{{u}_{i}}-{{S}_{i,m-1}}}{{{S}_{i,m}}-{{S}_{i,m-1}}},{{S}_{i,m-1}}<{{u}_{i}}<{{S}_{i,m}} \\ & ,{{u}_{i}}\ge {{S}_{i,m}} \\ \end{align} \right.$ | (1) |
式(1) 中:ui代表某重金属含量的实测值,Sij代表因子ui第j个评级等级的标准值,m是第m级评价标准.
3) 权重确定.常用的赋权重方法有聚类权法和超标法,文中采用聚类权法,即污染因子的实测浓度与其相应分级标准的比值来确定,由于各个因子毒性系数不同,各个因子对环境的贡献存在差异,有必要将毒性系数纳入权重考虑,以反映浓度和毒性的综合作用;设权重模糊子集A,记A={W1j,W2j,…,Wnj},Wij是第i个评价指标在第j个级别的权重,将权重归一化,公式如下:
| ${{W}_{ij}}=\frac{\frac{{{u}_{i}}\times T_{r}^{i}}{{{S}_{i}}}}{\sum\limits_{i=1}^{n}{\frac{{{u}_{i}}\times T_{r}^{i}}{{{S}_{i}}}}}$ | (2) |
式(2)中:ui为该指标的实测值,Si为该指标对应的级别的标准值,Tri为第i种指标的毒性系数.
4) 综合评价.首先采用矩阵A的元素分别与矩阵R各列中对应的元素相乘得到采样点处单个重金属的评价值,然后采用加权平均模型进行综合评价,加权平均模型将采样点处单个重金属的评价值求和,得出多因子综合评价的结果BJ,公式如下:
| ${{B}_{J}}=\sum\limits_{i=1}^{n}{{{W}_{i}}{{r}_{ij}}}$ | (3) |
式(3)中:BJ为综合评判结果,Wi为对应的权重,rij为模糊关系矩R中对应的元素,n为参评因子数目.
5) 评价分值. 由于采样点可能具有2个相同或相近的最大隶属度值,因此仅使用最大隶属度评价环境质量等级结果可能会存在误差,为了使结果更准确,更有参考价值,对每个采样点进行评价分值,评价分值是利用综合评价结果BJ的等级形成权重,对各等级的分值进行加权平均,得到每个采样点的评价分值,公式如下:
| $\begin{align} & c=\sum\limits_{j=1}^{n}{{{\delta }_{j}}{{C}_{j}}} \\ & {{\delta }_{j}}=\frac{b_{j}^{2}}{\sum\limits_{j=1}^{3}{b_{j}^{2}}} \\ \end{align}$ | (4) |
式(4)中:δj实际上构成一组权重,Cj 对第j 级环境质量水平所给的分值,bj是评价向量B中对应于第j 级环境质量水平的值,C是最终得分.
2 应用实例 2.1 研究区概况江西省信丰县,位于江西省赣州中部,居贡水支流桃江中游,地处东经114°34'~115°19',北纬24°59'~25°33',信丰矿藏资源丰富,为江西南部资源大县之一,煤炭储量和稀土品位居赣南之首,已发现的矿藏有35种,矿藏地137处. 137处矿藏地中,有大型矿床2处(1处共生矿床),中型矿床1处,小型矿床9处(1处共生矿床),矿点115处和矿化点10处[18]. 离子型稀土矿山开发经过40 多年的发展,经历了池浸、堆浸和原地浸矿3种采矿工艺的变迁[19],但由于采矿工艺落后,浸矿后任意堆积的残渣和尾矿中含有大量与稀土矿物伴生的重金属元素,通过沉降、雨淋、水洗等方式进入土壤[20-21],造成矿区土壤受重金属污染日益增加,因此矿区生态环境治理刻不容缓.
2.2 样品的采集和处理选取窑下、赤岗、烂泥坑和虎山4个矿区,共设28个土壤质量监测点,为使土壤样本具有代表性,在每个矿区的矿区外上游、拟开采的浸矿采场、历史浸矿采场、历史浸矿采场下游、历史堆池浸采场、历史堆池浸采场下游和矿区外双石头附近农田等7处进行选点(图 1).
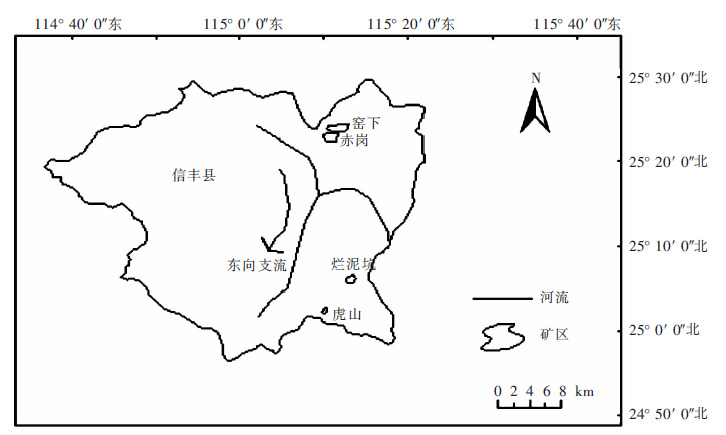 |
| 图 1 研究区概况 Fig. 1 Location of study area |
2.3 样品处理
土壤样品由江西理工大学化学分析实验室采用各类仪器分析重金属元素的含量,玻璃电极法测定pH值;样品中的Cd、Cr、Cu、Ni和Pb等5种重金属元素用HCl+HNO3+HClO4消解后[22],采用石墨炉原子吸收分光光度法测定;Zn、As等2种金属元素用HNO3+HClO4+HF3酸消化后[23],采用等离子体原子发射光谱法测定;Hg用HNO3+KMNO4消解后,采用冷原子吸收法测定[22].
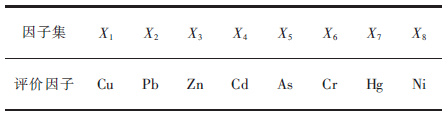
2.4 模糊数学应用分析1) 构建评价因子集和评价集.文中主要研究重金属Cu、Pb、Zn、Cd、As、Cr、Hg、Ni的污染程度,设这8种元素作为评价因子集X,记为X={Cu、Pb、Zn、Cd、As、Cr、Hg、Ni}(表 1),以《土壤环境质量标准》(GB15618—1995) 为参考依据,将评价等级分为3级,记V={V1,V2,V3},另外根据HaKanson的计算原则,结合陈静生的计算方法,给出了8种重金属的毒性系数(表 2).
| 表1 评价目标的因子集X Table 1 Factors set X of evaluation objectives |
 |
| 点击放大 |
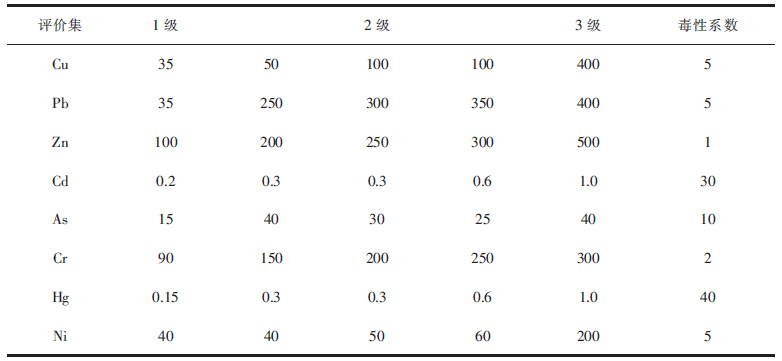
| 表2 评价目标的评价集V Table 2 Evaluation set V of evaluation objectives |
 |
| 点击放大 |
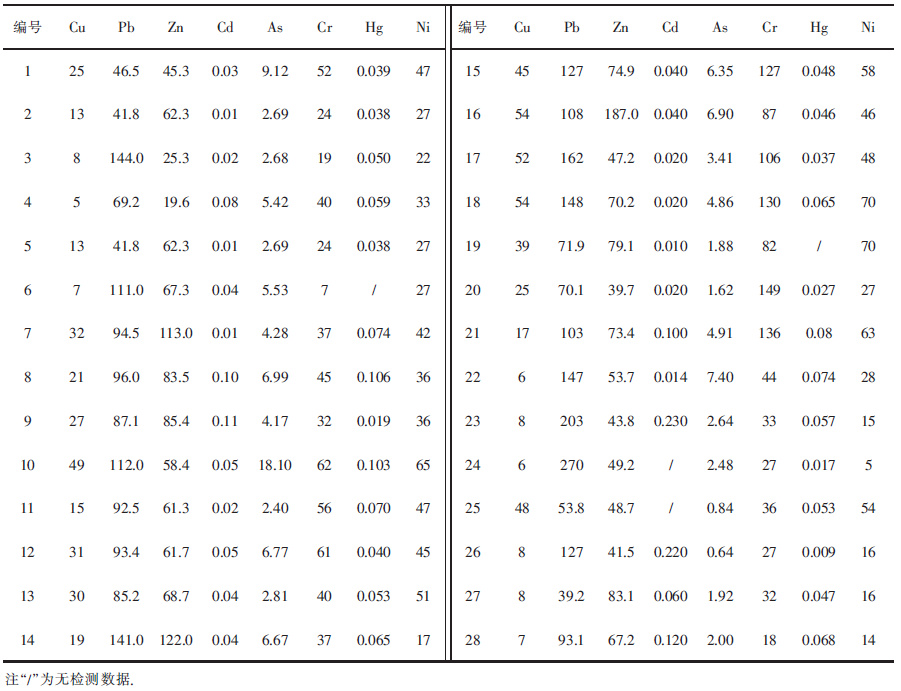
2) 建立模糊关系矩阵. 各种重金属对1级、2级、3级土壤重金属环境质量的隶属度函数用式(1) 表示,依据重金属的含量值(表 3)和各个等级的标准值建立模糊关系矩阵R,如1号采样点的模糊关系矩阵(表 4),同样方法计算其他采样点的模糊关系矩阵.
| 表3 重金属的含量值/(mg·kg-1) Table 3 Value content of heavy metals /(mg·kg-1) |
 |
| 点击放大 |
| 表4 1号采样点的模糊关系矩阵 Table 4 Fuzzy relation matrix on sampling point of 1 |
 |
| 点击放大 |
3) 确定各评价因子的权重. 依照式(2) 计算各个采样点处重金属的权重值,如1号采样点的权重矩阵W(表 5),同样方法计算其他采样点的权重集.
| 表5 1号采样点的权重集 Table 5 Right on sample weight set point of 1 |
 |
| 点击放大 |
4) 建立综合评价模型. 依照式(3) 和式(4) 建立最终模糊判断集合,对评价结果进行归一化处理,得到各采样点的评价向量,最大值所对应的级别为最终评价结果.评价分值根据土壤环境质量标准,1级土壤水平的分值为100,2级土壤水平的分值为80,3级土壤水平的分值为60;从评价分值可以直观地看出各采样点土壤重金属环境质量的优劣(表 6).
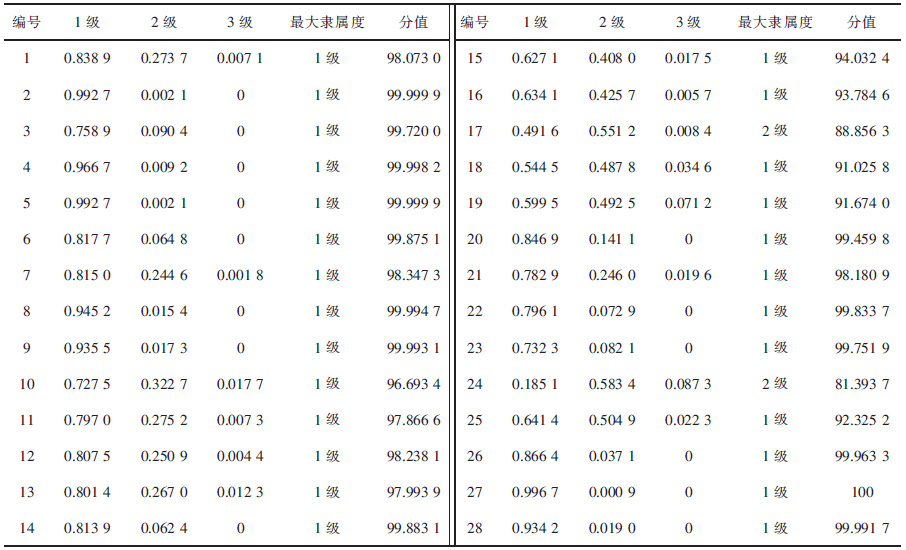
| 表6 采样点土壤重金属环境质量评价结果 Table 6 Heavy metals in soil sampling point environmental quality evaluation results |
 |
| 点击放大 |
按照最大隶属度原则,评价各个采样点的土壤重金属环境质量等级,由模型结果可以看出,除在采样点17、24两处的环境质量等级为2级外,其余采样点处的等级都为1级,采样点18、19、25三处的1级和2级综合评价值相差不大,1级值略微高于2级的值,等级相同的不同采样点之间分值相差不大,评价等级为1级的分值较高于评价等级2级、3级的分值,综合得出矿区土壤质量等级为1级,评价分值为97.034.
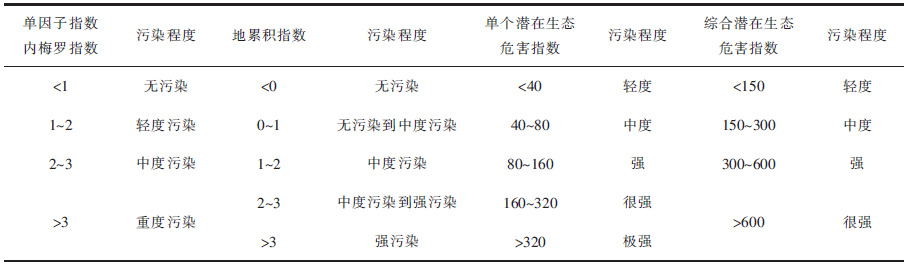
3 各评价方法对比分析 3.1 传统污染指数法1) 单因子污染指数[1-2]评价即对土壤中的某一污染物的污染程度进行评价,单因子污染指数等级划分标准见表 7,单项污染指数表达公式如下:
| ${{P}_{i}}={{C}_{i}}/{{S}_{i}}$ | (5) |
式(5) 中Ci为土壤重金属的实测浓度值;Si为污染物的评价标准值.
| 表7 土壤重金属污染等级划分标准 Table 7 Heavy metals contaminated soil classification standard |
 |
| 点击放大 |
2) 内梅罗综合指数法能够综合地反映土壤的污染程度[3-4],内梅罗综合指数等级划分标准见表 7,表达公式如下:
| $\begin{align} & {{P}_{综}}={{\left[ \left( P_{ave}^{2}+P_{\max }^{2} \right)/2 \right]}^{\frac{1}{2}}} \\ & {{P}_{ave}}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{W}_{i}}{{P}_{i}}} \\ & {{P}_{\max }}=Max\left( {{W}_{i}}P \right) \\ & {{W}_{i}}={{T}_{i}}/\sum\limits_{i=1}^{n}{{{T}_{i}}} \\ & \sum\limits_{i=1}^{n}{{{W}_{i}}}=1 \\ \end{align}$ | (6) |
式(6) 中:将单个重金属的毒性系数除以Ti的总和得到Wi,Wi表示第i种污染因子的权重.
3) 地累积指数[5-6]不仅能反映重金属分布的自然变化特征,而且可以判别人为活动对环境的影响,是区分人为活动影响的重要参数,地累积指数等级划分标准见表 7,表达公式如下:
| ${{I}_{geo}}={{\log }_{2}}\left( {{C}_{n}}/A{{B}_{n}} \right)$ | (7) |
式(7) 中:Cn为样品中元素n的浓度,Bn为中国土壤重金属元素背景值,A为修正指数,一般取1.5,通常用来表征沉积特征、岩石地质及其它影响.
4) 生态风险指数法通过土壤中重金属的含量值与土壤中重金属的背景值比值得到单项污染指数,然后引入重金属的毒性系数,得到潜在生态危害指数[7-8]. Eri为沉积物中第i种重金属的生态危害指数,RI为多种金属的生态危害指数,生态风险指数等级划分标准见表 7,表达公式如下:
| $RI=\sum\limits_{i=1}^{n}{E_{r}^{i}}=\sum\limits_{i=1}^{n}{T_{r}^{i}\centerdot C_{f}^{i}}=\sum\limits_{i=1}^{n}{T_{r}^{i}\centerdot \frac{C_{s}^{i}}{C_{n}^{i}}}$ | (8) |
式(8) 中:Tri为第i种重金属的毒性系数,反映第i种重金属的毒性水平和生物对其污染的敏感程度;Mfi为第i种重金属的富集系数,Csi为第i种重金属浓度实测值,Cni为中国土壤重金属元素背景值.
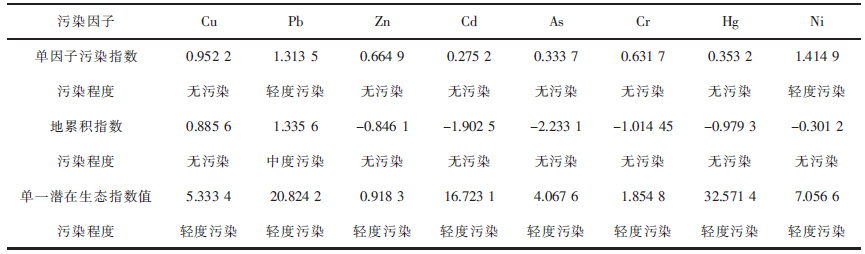
3.2 污染评价模型的对比分析将重金属含量值代入式(5) ~式(8) 中,评价结果见表 8,Pb、Ni的平均单因子污染指数大于1,表示受到轻度污染,Cu的平均单因子污染指数接近1,表示处于警戒线处,Pb的平均地积累指数值大于1,污染等级为2级,污染程度属于中度污染,8种重金属的单一潜在生态危害平均指数值都小于40,污染程度都为轻度,其中Hg的单一潜在生态危害平均指数值最高,内梅罗指数值为0.139 4,小于1,污染程度为未污染,综合潜在生态危害指数值为89.349 4,小于150,污染程度为轻微生态危害. 研究区评价方法的结果略有差异,原因可能是评价标准不同,模糊数学方法得到的结果(表 6)和其他传统的污染指数法得到的结果较为接近,综上所述信丰矿区土壤基本无污染,矿区土壤质量良好.
| 表8 矿区土壤重金属的污染特征 Table 8 Mining pollution characteristics of heavy metals |
 |
| 点击放大 |
3.3 污染评价模型的应用分析
单因子污染指数法和地累积指数法没有考虑土壤重金属的毒害性,评价方法只针对某一个元素而言,内梅罗污染指数引入了重金属的毒性系数,反映土壤综合环境质量,潜在生态危害指数法虽然引入重金属的毒性系数,反映单一重金属的污染状况和土壤综合环境质量,但忽略了多种重金属复合污染时各金属之间的加权或拮抗作用,该研究区域存在重金属元素复合污染. 模糊评价法采用聚类权法确定重金属的权重值,有效地克服了传统污染评价方法的不足,可以更有效地评估土壤的复合污染特征,同时也可以描述土壤污染评价的模糊性和渐变性.但模糊评价法计算量大,还需要进一步研究和改进.
4 结论1) 模糊评价法结果显示信丰县矿区土壤重金属无污染,矿区土壤质量良好. 近年来,矿区经历了池浸、堆浸和原地浸矿3种采矿工艺的变迁,残渣和尾矿大量堆积的现象逐步减少,通过沉降、雨淋、水洗等方式进入土壤中的重金属也减少了,矿区生态环境治理工作已经取得了很大的成效.
2) 模糊评价法可以综合评价矿区土壤污染状况,且引入重金属的权重系数,可以很好地反映重金属的实际污染程度. 通过最大隶属度原则评价出的污染等级可以反映同一采样点相邻级别隶属度大小的差异和土壤污染的渐变及发展趋势,体现了土壤质量评价中所存在的模糊性和渐变性特点. 各个等级的评价分值定量比较了各点的受污染程度,区分出相邻等级之间的差异,直观地表现了土壤环境质量的优劣. 因此模糊评价法可以作为一种有效的矿区土壤重金属元素污染程度的评价方法.
| [1] | 林世滔, 李琳, 卢志红, 等.基于GIS的江西省耕地土壤重金属污染评价研究[J]. 江西农业大学学报,2014,36 (5):1167–1172. |
| [2] | 王陆军, 范拴喜.宝鸡市城郊农田土壤重金属污染风险评估[J]. 中国农学通报,2015,31 (3):179–185. |
| [3] | 杨昱祺, 王小策, 孙淑蕊, 等.不同农业用地类型对土壤性质和土壤环境的影响——以北京市延庆县为例[J]. 水土保持通报,2014,34 (5):313–316. |
| [4] | 张鹏岩. 基于引黄灌区土地变化的可持续性评价研究[D]. 开封: 河南大学, 2013. http://cdmd.cnki.com.cn/article/cdmd-10475-1013351035.htm |
| [5] | 李真熠, 赵超凡, 杨志敏, 等.重庆市土壤重金属污染的功能分异评价[J]. 农业环境与发展,2013,30 (4):35–40. |
| [6] |
MULLER G. Index of geoaccumulation in sediments of the Rhine River[J].
Geojournal, 1969,2 (3):108–118. |
| [7] |
HAKANSON L. An ecological risk index for aquatic pollution control:A sedimentological approach[J].
Water Research, 1980,14 (8):975–1001. DOI: 10.1016/0043-1354(80)90143-8. |
| [8] | 高文文, 白中科, 余勤飞.煤矿工业场地土壤重金属污染评价[J]. 中国矿业,2015,24 (8):59–64. |
| [9] | 翟航, 卢文喜, 杨威, 等.模糊数学和污染指数法在土壤重金属污染中的应用[J]. 土壤,2008,40 (2):212–215. |
| [10] |
LIU L, ZHOU J Z, AN X L, et a1. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China[J].
Expert Systems with Applications, 2010,37 :2517–2521. DOI: 10.1016/j.eswa.2009.08.004. |
| [11] | 付善明, 肖方, 宿文姬, 等.基于模糊数学的广东大宝山矿横石河下游土壤重金属元素污染评价[J]. 地质通报,2014,33 (8):1140–1146. |
| [12] | 戴萍, 刘晓燕, 贾永英, 等.模糊数学在室内空气品质评价中的应用[J]. 大庆石油学院学报,2003,27 (4):90–92. |
| [13] | 杨海燕, 夏正楷.模糊数学在地下水资源污染评价中的应用[J]. 水土保持研究,2005,12 (4):107–109. |
| [14] | 李录娟, 邹胜章.不同权重确定方法对地下水质量评价的影响研究[J]. 人民长江,2014,45 (23):98–102. |
| [15] | 石晓翠, 钱翌, 熊建新.模糊数学模型在土壤重金属污染评价中的应用[J]. 土壤通报,2006,37 (2):334–336. |
| [16] | 徐鸿志, 常江.安徽省主要土壤重金属污染评价及其评价方法研究[J]. 土壤通报,2008,39 (2):411–415. |
| [17] | 朱青, 周生路, 孙兆金, 等.两种模糊数学模型在土壤重金属综合污染评价中的应用与比较[J]. 环境保护科学,2004,30 (3):53–57. |
| [18] | 王小玲, 王歆, 刘腾云, 等.江西主要类型重金属污染现状及修复实践[J]. 江西科学,2014,32 (5):594–599. |
| [19] | 罗才贵, 罗仙平, 周娜娜, 等.南方废弃稀土矿区生态失衡状况及其成因[J]. 中国矿业,2014,23 (10):65–70. |
| [20] | 许亚夫, 李银保, 陈海花.定南县废弃稀土矿区土壤中重金属元素Pb、Cr和Cu的测定[J]. 广东微量元素科学,2012,19 (10):10–14. |
| [21] | 王学刚, 王光辉, 刘金生.矿区重金属污染土壤的修复技术研究现状[J]. 工业安全与环保,2010,36 (4):29–31. |
| [22] | 王晓辉, 杨晨.基于GIS和地统计学的淮南矿区土壤重金属含量与空间分布研究[J]. 长江流域资源与环境,2014 (增刊1):60–65. |
| [23] | 符娟林, 章明奎, 厉仁安.基于GIS的杭州市居民区土壤重金属污染现状及空间分异研究[J]. 土壤通报,2005,36 (4):575–578. |
 2016, Vol. 7
2016, Vol. 7


