| 缓倾斜矿体采场结构参数优化数值模拟 |
2. 江西国泰五洲爆破工程有限公司,南昌 330038
2. Jiangxi Cathay Pacific Wuzhou Blasting Engineering Co. Ltd., Nanchang 330038, China
金属矿石回采中,矿柱留设关系到采场的稳定性,对矿山的正常运转起着至关重要的作用. 随着矿体的开采,原岩应力在受到扰动的情况下会重新分配,大部分会作用于矿柱[1],故矿柱尺寸的设计极为重要. 矿柱尺寸需同时满足安全生产和资源回收2个方面的要求,留设过大将导致回采率低,造成资源的浪费;留设过小则会导致冒顶事故,威胁工作人员的生命安全[2].
针对采场结构参数优化这一问题,国内外学者提出了多种方法,其中朱维申等[3]利用工程类比法确定了最佳的采场结构参数;杨朝[4]介绍了利用BP神经网络优化采场结构参数的方法;周科平等[5]介绍了利用遗传算法对采场结构参数进行优化的方法;J Munari和John G等[6-7]利用数值模拟的方法确定了最优采场结构参数方案;而Xing,J等[8]提出应用正交试验比较采场结构参数优劣的方法;文中以宁都硫铁矿的130 m中段为研究对象,利用ANSYS对矿体进行建模,导入FLAC3D后对各个开采方案进行模拟,综合比较模拟结果选择最优的采场结构参数.
1 矿山概况宁都硫铁矿矿体为缓倾斜矿体,位于宁都县境内. 该矿所处区域地质结构为向斜结构,向斜最高标高491.09 m,最低标高220 m,其中矿区所处区域标高100~350 m,地势相对平缓. 宁都硫铁矿矿床系矽卡岩型含铜磁黄铁矿床,倾角0°至30°之间,厚度系数变化大,其中最薄部位仅有1.0 m,最厚部位为21.37 m. 矿体上盘为灰岩和钙质砂岩,下盘为砂质板岩,整体稳定性较好. 宁都硫铁矿采用房柱法开采矿床,地质条件的复杂导致采场结构参数难以合理选择.为保证矿井生产的安全与高效,文中利用ANSYS建立模型并导入FLAC3D中对多组开采方案进行模拟运算,综合比较计算结果得出最优采场结构参数用以指导实际生产.
2 采场结构参数理论计算 2.1 矿柱载荷宁都硫铁矿采用房柱法进行开采,采矿方法如图 1所示.
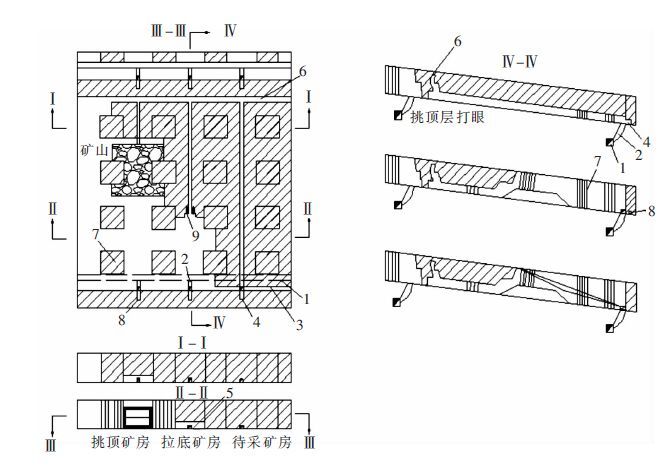 |
| 1. 运输巷道; 2. 放矿溜井; 3. 切割平巷; 4. 电耙硐室; 5. 上山; 6. 联络平巷; 7. 矿柱; 8. 电耙绞车; 9. 炮孔. 图 1 采矿方法示意 Fig. 1 Mining method diagram |
大量研究表明采用房柱采矿法时,矿柱的破坏一般由上覆岩层重力的垂直应力产生. 为计算方便将矿柱简化为正方形,利用面积承载理论可知矿柱载荷σu的计算公式如下[9].
| ${{\sigma }_{u}}=\gamma H\left( \frac{B}{L}+1 \right)\left( \frac{b}{n}+1 \right)$ |
其中:γ为上覆岩层重度,单位为N/m;H为开采深度,B为矿房跨度,L为矿柱宽度,b为矿柱间距,n为矿柱长度,单位为m.
2.2 矿柱强度矿柱的强度随着矿柱的岩体地质结构、矿柱尺寸、几何形状等的变化而变化,对此国内外进行了大量的试验和研究,并提出了多种理论计算方法[10-12],文中运用Bieniawski提出的强度公式,计算矿柱的理论强度σp:
| ${{\sigma }_{p}}={{\sigma }_{0}}{{\left( 0.64+0.36\frac{L}{n} \right)}^{a}}$ |
其中:σ0为试样的单轴抗压强度,单位为MPa;L为矿柱宽,h为矿柱高,单位均为m;a为常数,与h/L有关:当h/L<5时,a=1;当h/L>5时,a=1.4.
2.3 矿房极限跨度矿房极限跨度指在保证空区安全的条件下的最大矿房跨度[13]. 文中结合矿山监测数据,得到矿房走向极限跨度计算公式如下:
| ${{B}_{极限}}=\frac{4.5\left( \lambda \rho H+{{\sigma }_{允许}} \right)}{\rho H\left( 1-0.8\lambda \right)-0.8{{\sigma }_{允许}}}$ | (1) |
式(1)中:B极限为矿房极限跨度,单位为 m;ρ为上覆岩层容重,取ρ=3 476 kg/m3;H为矿体埋深,取H=150 m;λ为测压系数,取λ=0.39.
根据矿山实际情况,顶板的安全系数取值n=1.2,结合式(1),可得矿房的走向极限跨度为14.22 m.
3 FLAC3D模型的建立 3.1 模型力学参数的选择模型物理力学参数的选择影响着模拟计算的准确性[14]. 由地质报告得知矿体的上盘主要为灰岩,下盘主要为砂岩,通过室内试验得到岩石试件的原始力学参数,再结合现场实际进行必要的强度折减后,最终取得数值模拟使用的岩体力学参数,如表 1所列.
| 表1 岩体力学参数 Table 1 Mechanical parameters of rock |
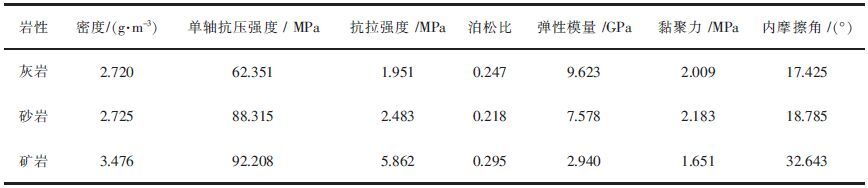 |
| 点击放大 |
3.2 试验方案的确定
采场结构参数的优化旨在保持采场安全的条件下获得最大的矿石回采率[15]. 选取矿柱间距、矿柱尺寸、矿房跨度和顶板厚度作为控制变量,并结合理论计算与实践经验设计9组正交实验方案,详细内容如表 2所列.
| 表2 正交试验方案参数 /m Table 2 Orthogonal test scheme /m |
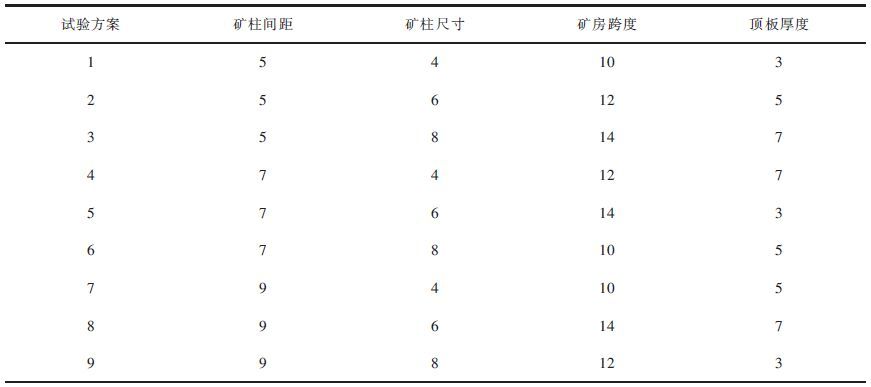 |
| 点击放大 |
3.3 矿体模型的建立
为备选方案中确定最优方案,文中选用部分采场作为研究对象,利用ANSYS进行数值建模,并导入FLAC3D软件中进行数值计算,分别从应力、位移、塑性区3个方面分析计算结果,得出最终方案.考虑到开采扰动区域的大小,模型长度取值500 m,宽度取值300 m,高度取值300 m;矿体模型走向长度即模型长度,倾向长度即模型宽度,厚度取值4 m,倾角取值15°,最大埋深140 m.选择135 m中段及上一中段中部沿走向150 m范围内的矿体进行模拟开挖. 模型中采场沿矿体走向布置,跨度参见表 2,采高为4 m,矿块开采方式选用“由中间到两边”、“隔一采一”的原则,具体采场布置详见图 2、图 3.
 |
| 图 2 矿房布置俯视图 Fig. 2 Top view of room layout diagram 有色金属科学与工程 |
 |
| 图 3 矿房布置侧视图 Fig. 3 Side view of room layout diagram |
3.4 边界条件与初始应力场的设置
因建立模型时已考虑到了开采的扰动范围,故只需增加模型表面的约束即可.该模型选用位移约束,分别约束左右、前后四面的水平位移以及底面的垂直位移,顶面则设置为自由面.
由矿山实际地质报告得知宁都硫铁矿的构造应力较小,故根据前苏联学者金尼克的假说,只考虑岩体自重应力而忽略构造应力,利用理论计算得到垂直应力σh和水平应力σv[16-17],计算公式如下:
| ${{\sigma }_{h}}=\rho H$ | (2) |
| ${{\sigma }_{v}}=\lambda {{\sigma }_{h}}$ | (3) |
式(2)、式(3)中:ρ为上覆岩层容重,H为岩体的埋深,λ为测压系数,根据实际情况取0.39.
结合矿山地质资料与式(2)和式(3),在模型的顶面设置4.01 MPa的垂直应力,侧面设置1.68 MPa的水平应力.
4 结果分析大量研究证明顶板的下沉量与塑性区的分布状态对采场的稳定性有重要影响[18-20],文中分别从顶板下沉量和模型塑性区的分布2个方面对各个方案进行比较,由于篇幅限制仅给出部分计算结果和数值云图.
4.1 顶板下沉量由于顶板下沉量对工作面的正常生产以及人员安全有重要影响,故利用FLAC3D计算各方案顶板下沉量,结果如图 4、图 5所示.
 |
| 图 4 方案1开挖后顶板位移 Fig. 4 Roof displacement of program 1 |
 |
| 图 5 方案8开挖后顶板位移 Fig. 5 Roof displacement of program 8 |
分析图 4、图 5可知:矿体开挖后,采场出现“顶板下沉” 与“底板上鼓”的现象,且拱径越小,位移量越大.各方案垂直位移分别为:方案1为32.23 mm;方案2为6.76 mm;方案3为40.00 mm;方案4为10.00 mm;方案5为31.66 mm;方案6为5.84 mm;方案7为118.00 mm;方案8为9.80 mm;方案9为13.14 mm. 其中方案7位移量最大,方案6最小.
运用极差理论分析,将其中各因素分为3个水平,矿柱间距分为5 m、7 m、9 m 3个水平;矿柱尺寸分为4 m、6 m、8 m 3个水平;矿房跨度分为10 m、12 m、14 m 3个水平;顶板厚度分为3 m、5 m、7 m 3个水平,分别求出每个因素各水平的极差,并以此判断各因素对顶板位移的影响程度,分析结果见表 3.
| 表3 顶板位移因素极差分析结果 /mm Table 3 Analysis results of displacement range of top plate /mm |
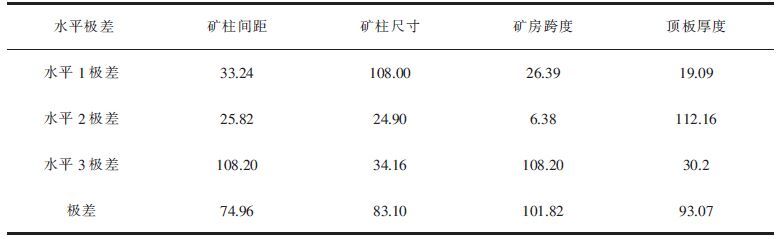 |
| 点击放大 |
通过对表 3的分析可知,矿房跨度影响最大,顶板厚度其次,矿柱尺寸再次,矿柱间距最小.故在需要严格限制顶板下沉的区域,矿房跨度的留设应相应减小.
4.2 塑性区分布由于塑性区体积可体现矿岩的破坏程度,尤其是顶板的塑性区直接关系到采场的稳定性,故文中将顶板塑性区分布结果进行显示,如图 6、图 7所示.
 |
| 图 6 方案1开挖后顶板塑性区 Fig. 6 Roof plastic zone after excavation of program 1 |
 |
| 图 7 方案8开挖后顶板塑性区 Fig. 7 Roof plastic zone after excavation of program 8 |
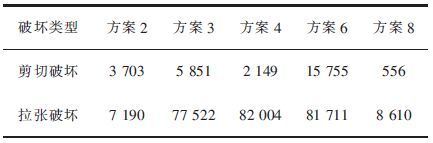
根据顶板塑性区分布情况得知,方案1、方案5、方案7、方案9中顶板塑性区范围较大会导致顶板的破坏,生产安全无法保障,故在方案选择中应排除这4个方案. 调用FLAC3D内置函数,得出其他方案的塑性区体积,结果如表 4所列.
| 表4 各方案塑性区体积 /m3 Table 4 Plastic zone volume of each program /m3 |
 |
| 点击放大 |
5 各方案综合比较
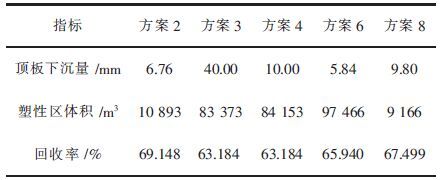
采场结构参数优化旨在保证采场安全的情况下争取最大的回采率,故各方案的综合比较的内容分别包括经济指标和安全指标,其中,经济指标主要指回收率,安全指标主要指塑性区体积与顶板沉降量. 由于方案1、方案5、方案7、方案9顶板塑性区相互贯通,顶板已发生严重破坏,采场安全无法保证,故不进行比较. 其余各方案顶板下沉量、塑性区体积、回收率如表 5所列.
| 表5 各方案综合指标 Table 5 Comprehensive index of each program |
 |
| 点击放大 |
分析表 5可知各方案优越性相互交叉,无法直接通过计算结果对方案进行优选,故运用层次分析法对各方案进行综合评价,计算得到各指标的权重,如表 6所列.
| 表6 各指标权重 Table 6 Weight table of each index |
 |
| 点击放大 |
根据表 6计算综合比较的权重向量如下:
| $W = \left[ {\matrix{ {0.136} & {0.449} & {0.415} \cr } } \right]$ |
规格化方案综合指标表,可构建隶属度矩阵R:
| $R = \left[ {\matrix{ {0.846} & {0.146} & {0.584} & 1 & {0.596} \cr {0.841} & {0.110} & {0.109} & {0.094} & 1 \cr 1 & {0.914} & {0.914} & {0.954} & {0.976} \cr } } \right]$ |
结合以上所得结果,可得本次综合比较的评判向量B:
| $B = W \times R = \left[ {\matrix{ {0.910} & {0.448} & {0.508} & {0.574} & {0.935} \cr } } \right]$ |
根据结果得知各方案的得分,并进行优越性的排序,结果为:方案8→方案2→方案6→方案4→方案3,其中方案8得分最高,故为最优方案,在实际生产中应优先选择.
6 结论结合宁都硫铁矿的实际生产情况,对矿山的生产过程进行了数值模拟. 分析计算结果得知矿房的跨度对顶板位移量的影响最大. 运用层次分析法得出影响采场安全和矿山经济因素的权重,并以此对9组方案进行综合比较,最终确定方案8为最优方案,其具体参数为:点柱间距取9 m,点柱尺寸取6 m,矿房跨度取14 m,顶板厚度取7 m. 优化所得方案对实际采场布置提供了理论依据.
| [1] | 宋卫东, 曹帅, 付建新, 等.矿柱稳定性影响因素敏感性分析及其应用研究[J]. 岩土力学,2014 (增刊1):271–277. |
| [2] | 王宏岩.矿柱稳定性对矿柱回收的影响[J]. 中国矿山工程,2012,41 (4):21–23. |
| [3] | 朱维申, 李术才, 程峰, 等.能量耗散模型在大型地下洞群施工顺序优化分析中的应用[J]. 岩土工程学报,2001,23 (3):333–336. |
| [4] | 杨朝晖, 刘浩吾.地下工程围岩稳定性分类的人工神经网络模型[J]. 四川大学学报(工程科学版),1999,3 (4):66. |
| [5] | 周科平.采场结构参数的遗传优化[J]. 矿业研究与开发,2000,20 (3):7–10. |
| [6] | MUNARI J. Stope design within a final pillar retreat sequence at xstrata copper's mount Isa copper mines[C] //The AusIMM New Leaders' Con ference 2007 Proceedings, 2007: 45-52. |
| [7] |
JOHN G, HENNING, HANI S MITRI. Assessment and control of ore dilution in long hole mining: case studies[J].
Geotechnical and Geological Engineering, 2008,26 (4):349–366. DOI: 10.1007/s10706-008-9172-9. |
| [8] |
GUILLERMO S T, JUAN E T, PEDRO P L, et al. Dendroid: A text mining approach to analyzing and classifying code structures in Android malware families[J].
Expert Systems with Application, 2014,41 (1):1104–1117. |
| [9] | 彭斌, 陈才贤, 杨军伟.石膏矿矿柱稳定性分析及试验研究[J]. 采矿技术,2011 (2):18–21. |
| [10] |
ESTERHUIZEN G S, DOLINAR D R, ELLENBERGER J L, et al. Pillar strength in underground stone mine in the United States[J].
International Journal of Rock Mechanics and Mining Sciences, 2011,48 (1):42–50. DOI: 10.1016/j.ijrmms.2010.06.003. |
| [11] | JIANG Y D, WANG H W, ZHAO Y X, et al. The influence of roadway backfill on bursting liability and strength of coal pillar by numerical investigation[C]//The First International Symposium on Mine Safety Science and Engineering, 2011: 1260-1278. |
| [12] | 郭汉燊.矿柱强度的若干影响因素[J]. 岩石力学与工程学报,1993 (1):38–45. |
| [13] | 杨秀明.用砼柱置换原生矿柱的研究[J]. 采矿技术,2011 (4):25–27. |
| [14] | 周伟永, 饶运章, 汪弘, 等.基于FLAC3D的采场稳固性数值模拟研究[J]. 矿业研究与开发,2014 (2):13–17. |
| [15] | 武永猛. 凡口铅锌矿顶底柱矿体安全高效回采工艺研究[D]. 长沙中南大学, 2013. http://cdmd.cnki.com.cn/article/cdmd-10533-1014141487.htm |
| [16] | 金小川, 周宗红, 陈学辉, 等.浅谈原岩应力及测量方法[J]. 矿产与地质,2012,26 (5):363–365. |
| [17] | 迟兵, 吕力行, 高义军, 等.原岩应力的理论分析及数值模拟[J]. 黄金,2013,34 (3):35–38. |
| [18] | 叶海旺, 常剑, 周磊.基于FLAC3D的采场结构参数优化[J]. 金属矿山,2010 (12):6–8. |
| [19] | 曹宗权, 邵海, 高卫宏, 等.基于FLAC3D的下向进路胶结充填采场参数研究[J]. 有色金属科学与工程,2011,2 (6):74–78. |
| [20] | 崔栋梁, 李夕兵, 赵国彦.新城金矿难采矿体采场结构参数数值模拟分析[J]. 江西有色金属,2006 (3):13–17. |
 2016, Vol. 7
2016, Vol. 7


