| 几种信号去噪方法在爆破振动信号中的应用分析 |
2. 中南大学西部矿业博士后科研工作站,西宁810006
2. Postdoctoral Scientific Research Workstation, Western Mining Co. Ltd., Central South University, Xining 810006, China
在爆破振动信号监测时,由于受到外部环境的干扰,监测结果不可避免地与实际信号存在误差,直接影响爆破振动信号分析的精度,为了使获取的爆破振动信号更准确地反映爆破效果,必须对原始信号进行去噪. 爆破地震波作为一种非平稳信号,去噪方法有很多,基于小波分析的去噪方法主要有小波分解与重构去噪[1]、小波阈值法去噪[2]、平移不变量小波去噪[3]、小波变换模极大值法去噪[4]等,以及经以上4种方法改进的小波分析去噪法[5-7];其中文献[8]表明,小波分解与重构法仅仅适用于确定性噪声情况下,对于含有白噪声去噪效果非常差;小波阈值法去噪过程会出现伪吉布斯现象,但噪声能基本上被消除,且计算时间短;小波变换模大极值法与平移不变量小波去噪性能较前2种方法更为理想,缺点在于计算量大,时间过长. 基于经验模态分解去噪分析的主要有 EMD (Empirical Mode Decomposition)[9-10]与 EEMD(Ensemble Empirical Mode Decomposition)去噪法[11],EMD即Huang提出的经验模态分解[12],信号的非线性以及非平稳特性在EMD分析过程可以较为完整的保全下来,因此,该方法在信号去噪与滤波中得到广泛应用;EEMD去噪原理与EMD相同,不仅拥有EMD分解时的自适应性,优点在于能消除模态混叠现象[13].
以上研究表明目前信号的去噪方法主要有小波分析与EMD 2大类,但其在爆破振动信号去噪领域内的优缺点报道甚少. 文中基于小波阈值去噪、EMD去噪以及EEMD去噪方法,研究3种去噪方法在爆破振动信号中的应用,并结合信噪比、均方根误差等参量对几种方法的综合去噪效果进行对比分析,给实际工程应用提供参考.
1 3种去噪方法的基本原理 1.1 小波阈值去噪方法对一个有限长信号与高斯白噪声进行叠加,则混叠后的信号可以表示为:
| ${x_t} = {y_t} + \sigma {z_t}$ | (1) |
式(1)中:xt为混叠噪声后的待处理信号;yt为有效信号;σ为噪声级;zt为标准高斯白噪声信号.
小波阈值法将xt中zt剔除的步骤如下:
第1步:爆破振动信号的分解,即选取合适的小波基将含噪信号xt进行N层小波分解,其中小波基与层次N的选取可以通过计算或者经验中得来.
第2步:对不同层数系数选择不同阈值进行阈值量化处理,将由zt衍生的系数过滤掉.
第3步:对量化后的小波系数重构,得到有效信号yt.
可以看出在以上3个步骤中,第1步与第2步是其核心,特别是分解时小波基与系数处理时阈值的选择,文献[14]表明在爆破振动信号去噪中Heursure函数效果最好.
1.2 EMD去噪方法EMD去噪方法基本原理是对原始信号进行分解与重构,所以EMD去噪法首要工作便是对信号进行经验模态分解[9],其主要步骤如下:
第1步:找出原始信号x(t)所有极值点,基于3次样条插值,构造出x(t)的极大值(上)包络线xmax(t)与极小值(下)包络线xmin(t).
第2步:将极大值包络线与极小值包络线的均值依次连接,得到一条均值线m1(t):
| ${m_1}\left( t \right) = \left( {{x_{\max }}\left( t \right) + {x_{\min }}\left( t \right)} \right)/2$ | (2) |
并求x(t)与m1(t)的差:
| ${h_1}\left( t \right) = x\left( t \right) - {m_1}\left( t \right)$ | (3) |
第3步:以h1(t)为原始信号,重复以上步骤k次,得到h1k(t),计算它与h1(k-1)(t)的标准差SD:
| $SD = \sum\limits_{t = 0}^T {\left| {\frac{{{h_{1k}}\left( t \right) - {h_{1\left( {k - 1} \right)}}{{\left( t \right)}^2}}}{{h_{1\left( {k - 1} \right)}^2\left( t \right)}}} \right|} $ | (4) |
若h1k(t)满足选取的SD值,记h1k(t)为c1(t),则认为c1(t)为第一阶分量,若不满足,重复以上步骤,直到满足为止.
第4步:计算残差r1(t).
| ${r_1}\left( t \right) = {x_1}\left( t \right) - {c_1}\left( t \right)$ | (5) |
视r1(t
| $x\left( t \right) = \sum\limits_{i = 1}^n {{c_i}\left( t \right) + {r_n}\left( t \right)} $ | (6) |
式(6)中:ci(t)为第i个IMF分量;rn(
信号经过EMD分解后将由从低到高多个频段的ci(t)组成,因此,通过剔除不同频段IMF分后再进行重构即可完成去噪.
1.3 EEMD去噪方法在进行EMD分解,由于间断信号、噪音等原因会产生模态混叠现象,为了消除这一现象,E Huang等[15]对原先的EMD方法进行改进,并衍生出基于EEMD分解的信号去噪方法,步骤如下:
第1步:在原始信号x(t)循环加入等长度的正太分布白噪声zi(t),并进行归一化处理,得到新的信号xi(t).
第2步:对于zi(t)进行EMD分解,得到IMF分量cij(t),其中i表示第i次加入后得到的IMF分量.
第3步:为了获得真实的IMF分量,需要消除前面所加入的白噪声,假设加入了N次,则真实分解结果可以表示为:
| ${c_j}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{c_{ij}}\left( t \right)} $ | (7) |
所加入的白噪声遵循如下规律:
| $e = \frac{\alpha }{{\sqrt N }}$ | (8) |
式(8)中:e为标准差,即输入信号与相应IMF分量重构结果的偏离;α为白噪声的幅值.可以看出N值取值与幅值α有关,但白噪声幅值对于分解结果影响不大,因此总体来说EEMD分析与人的主观介入不存在必然联系,仍然具有自适应性.
第4步:信号重构,与EMD方法相同. 通过以上分析可以得知EEMD消噪与EMD消噪区别在于2种方法所分解的IMF分量,EEMD分解通过在原始信号添加白噪声,消除了模态混叠效应.
2 爆破振动信号去噪分析 2.1 爆破振动信号去噪爆破振动测试采用加拿大Instantel公司生产的Blastmate III型测振仪.试验地点在江西省铅山县永平露天铜矿,测点布置在东部边坡,共监测到5组不同露天爆破条件下径向爆破振动信号,见图 1.
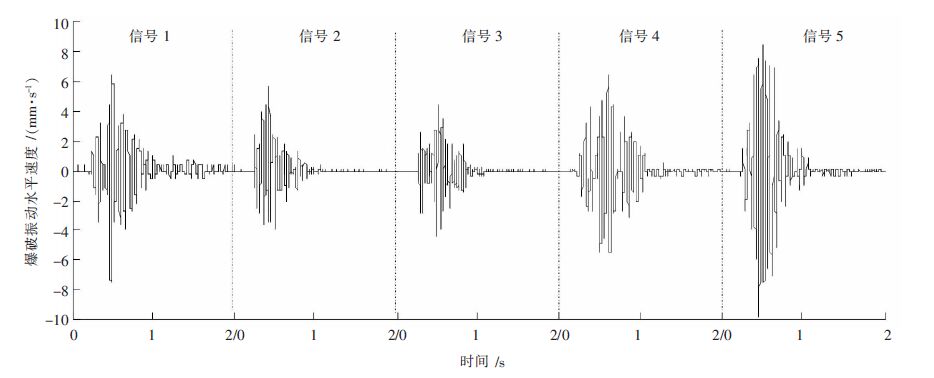 |
| 图 1 实测5 组爆破振动 Fig. 1 Five groups of blasting vibration signals |
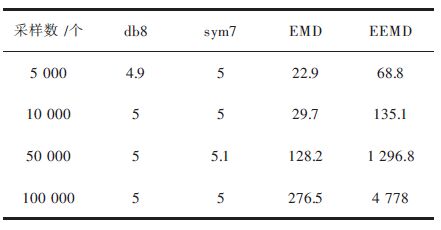
由图 1中可知所有信号源波形光滑度较差,均含有一定的噪音成分. 现采用小波阈值去噪法、EMD去噪、EEMD去噪分别对以上5组爆破振动信号进行去噪处理;①小波阈值去噪:小波家族中,db8[16]与sym7[17]在爆破振动信号分析中应用最为广泛,因此分别选用db8与sym7对源信号进行去噪,分解层次为4层,重构信号见图 2; ②EMD及EEMD去噪:基于Matlab14自编的 EMD与EEMD分解程序,首先采用上述程序分别对5组爆破振动信号进行经验模态分解与集成经验模态分解,滤去高频分量(即低通时空滤波),然后对保留的IMF分量进行重构,获得新的爆破振动信号,结果见图 3、图 4所示.以上去噪分析均基于Matlab14计算工具,计算机CPU为P6 000@1.87 Hz,内存4 GB.其中小波分析计算速度最快且与采样数无关,EMD次之,EEMD计算时间最长,详细计算时间见表 1.
| 表1 3 种去噪方法计算时间对比/s Table 1 Computer time contrast of three kinds of denoising method /s |
 |
| 点击放大 |
2.2 3种去噪方法结果分析
由图 2可以看出,使用小波阈值法处理爆破振动信号时,对于信号1、信号3与信号4去噪,sym7所取得效果较好;对于信号2与信号5去噪时,db8效果较好,即选取不同小波基函数将产生不同的去噪效果,并且无确定的规律性. 对比图 2、图 3、图 4与图 1源信号可以发现3种方法去噪所取得的波形都比较光滑,噪声基本被剔除. 其中,小波变换阈值去噪法对于信号1、信号4、信号5的去噪效果要明显好于处理信号2、信号3,信号2、信号3在局部仍然存在一定的幅度振荡. EEMD与EMD对所有信号去噪效果一致,不受信号源的影响,表现出它们在信号分析时的自适应性.
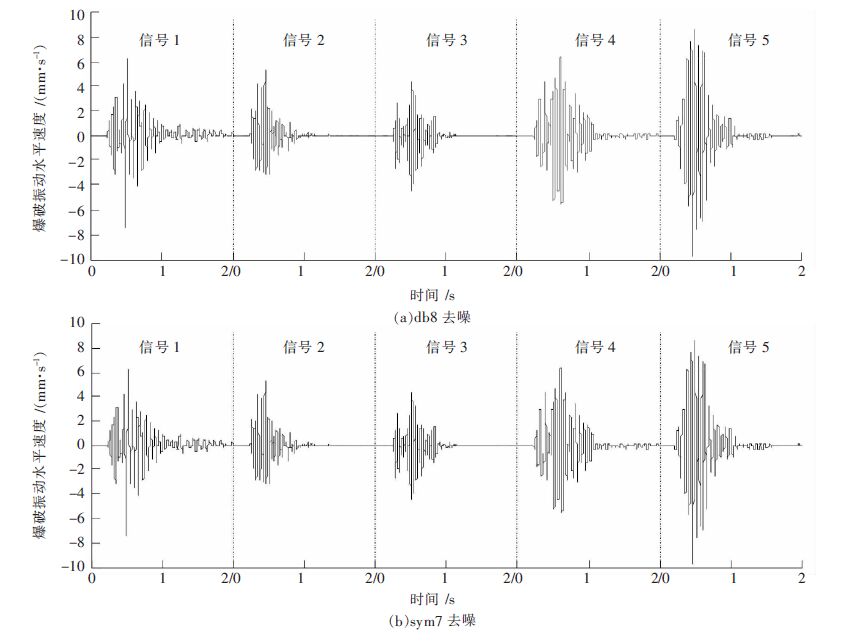 |
| 图 2 小波阈值法去噪信号 Fig. 2 Wavelet threshold denoising method signal |
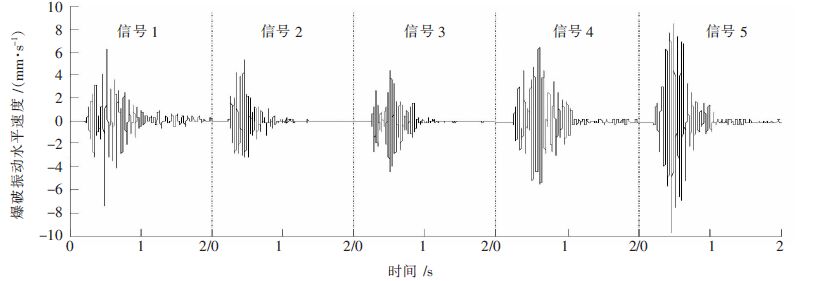 |
| 图 3 EMD 低通去噪信号 Fig. 3 EMD 低通去噪信号 |
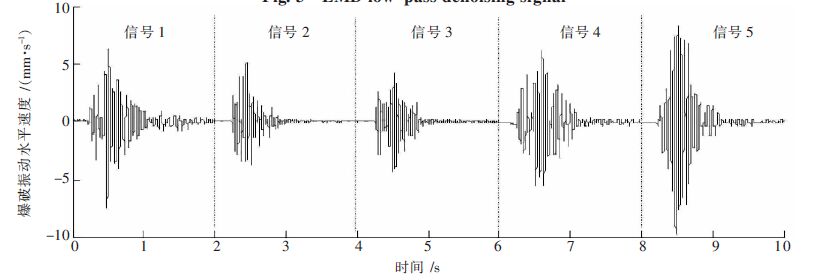 |
| 图 4 EEMD 低通去噪信号 Fig. 4 EEMD low-pass denoising signal |
基于能量叠加法[18]计算出3种信号去噪后信噪比SNR与均方根误差RMSE,见表 2,并作出各种方法信噪比变化趋势图,见图 5. 由图 5可以得知小波阈值法去噪信噪比曲线上下波动较大,当采用小波阈值(db8)法对信号1、信号4、信号5去噪时所获得的信噪比分别为22.8、24.79、26.85,其信噪比值与采用EEMD法相当;但当采用小波阈值(db8)法对信号2、信号3去噪时所获得的信噪比分别为14.71、15.08,信噪比值大幅度降低,低于EMD法去噪后信噪比;由图 5知当采用sym7小波基时信噪比值有略微变化,但整体趋势没有改变,以上表明小波阈值法在处理不同信号时,信噪比值波动幅度较大,去噪效果不稳定. 由图 5可以得出EMD与EEMD去噪后信噪比曲线变化趋势稳定,表明这2种方法对信号去噪时效果更稳定;由表 2可以得知,EEMD去噪后均方根误差平均值为0.076,为3种方法中最小,说明EEMD法去噪后信号最接近原始信号,去噪效果最好.
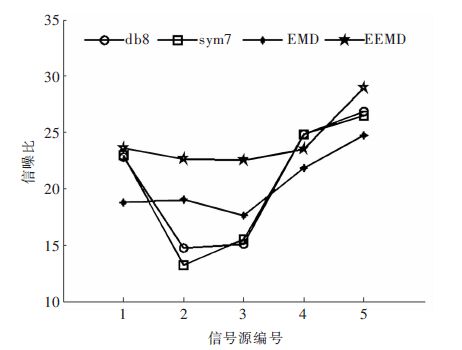 |
| 图 5 不同种方法去噪信噪比 Fig. 5 SNR of different methods denoising |
| 表2 3 种方法去噪SNR 与RMSE 的比较 Table 2 Comparison of SNR and RMSE based on three methods denoising |
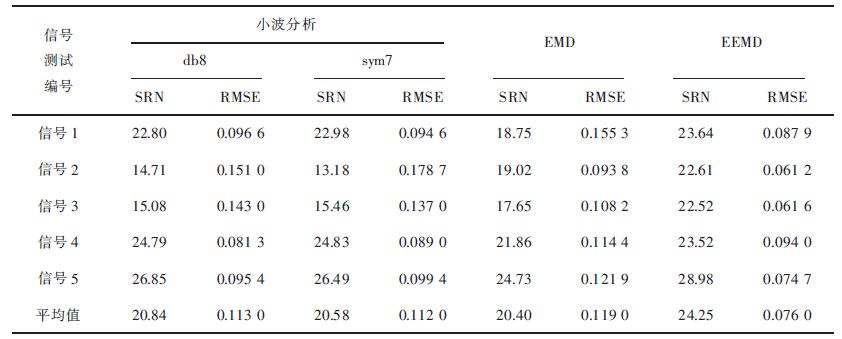 |
| 点击放大 |
3 讨 论
小波阈值法去噪基本过程为小波基的选取、基于该小波基函数分解、选取阈值过滤掉噪音引起的高频系数,最后基于该小波基函数重构. 其中小波家族中的小波基函数具有多样性,小波函数的正则性、波形与数据结构的相似度(即对称性)对最后去噪效果影响较大,要取得较好的去噪效果就必须选取具有较好正则性与对称性的小波基函数. 小波阈值的选取作为小波去噪法中的关键步骤,若阈值选取过大,则会消除原始信号的有用成分,若阈值选取过小,则原始信号的中的噪音成分会消除不干净. 以上分析表明若采用相同的小波基函数与阈值对不同信号处理时,其去噪效果必然参差不齐.
EMD与EEMD去噪分解过程使真实存在的不同尺度波动或趋势逐级分解开,产生一系列具有不同特征尺度的IMF分量,上述分解过程克服了小波分析中小波基选取的局限,因此它在处理信号时具有自适应性,对信号去噪时不受信号特征的变化,去噪效果稳定;由于EEMD能消除EMD在分解时会产生模态混叠现象,其去噪效果要明显好于EMD去噪.
4 结 论1)在使用小波变换阈值法、EMD法与EEMD 法对爆破振动信号去噪时,综合对比发现EEMD去噪效果最好,EMD与小波阈值法去噪效果相同,但稳定性存在差异.
2)采用小波变化阈值法对不同爆破参数下地震波信号处理时,受小波基函数与阈值选取规则的影响,去噪效果相差甚大,并且尚无发现确定性的规律,基于以上原因,小波阈值法对爆破振动信号去噪在实际工程中会受到一定限制.
3)EMD与EEMD由于对信号的分析有其自适应性,所以在对信号源去噪时取得效果的稳定性好,EEMD因为在分解IMF分量时消除了EMD存在的模式混叠现象,其去噪效果要好于EMD,但在使用EEMD去噪时计算量非常庞大,耗时较长
致谢: 本研究由国家自然科学基金资助项目(51404111)、中国博士后科学基金资助项目(2014M562529XB)、江西理工大学重点学科资助项目(3304000004)资助,在此表示感谢!本文的现场试验工作得到江铜集团永平铜矿领导和生产技术部、露天采场等部门的大力支持和帮助,在此向他们致以衷心的感谢!| [1] | 高勇军, 陈小波, 王伟, 等.小波分析在爆破地震信号降噪中的应用[J]. 爆破,1999 (3):9–12. |
| [2] | 倪瑛, 林植平.小波分析及其去噪应用[J]. 南京工业职业技术学院学报,2008 (2):21–22. |
| [3] | 熊正明, 中国生, 徐国元.基于平移不变小波爆破振动信号去噪的应用研究[J]. 金属矿山,2006 (2):12–14. |
| [4] | 刘丽梅, 刘齐跃, 张静.基于小波变换模极大值的去噪方法研究[J]. 河北工业科技,2010 (6):367–372. |
| [5] | 陈晓曦, 王延杰, 刘恋.小波阈值去噪法的深入研究[J]. 激光与红外,2012 (1):105–110. |
| [6] | 徐学勇, 程康.爆破震动信号模极大值小波消方法的改进[J]. 爆炸与冲击,2009 (2):194–198. |
| [7] | 王拴中, 朱玉田.改进小波阈值去噪法的对比性仿真实验与分析[J]. 噪声与振动控制,2012 (1):128–132. |
| [8] | 文莉, 刘正士, 葛运建.小波去噪的几种方法[J]. 合肥工业大学学报(自然科学版),2002 (2):167–172. |
| [9] | 李夕兵, 张义平, 左宇军, 等.岩石爆破振动信号的EMD滤波与消噪[J]. 中南大学学报(自然科学版),2006 (1):150–154. |
| [10] | 王维强, 杨国权.基于EMD与ICA的地震信号噪技术研究[J]. 石油物探,2012 (1):19–29. |
| [11] | 赵明生, 梁开水, 罗元方, 等.EEMD在爆破振动信号去噪中的应用[J]. 爆破,2011 (2):17–20. |
| [12] | 徐晓刚, 徐冠雷, 王孝通, 等.经验模式分解(EMD)及其应用[J]. 电子学报,2009 (3):581–585. |
| [13] | 赵玲, 刘小峰, 秦树人, 等.消除经验模态分解中混叠现象的改进掩膜信号法[J]. 振动与冲击,2010 (9):13–17. |
| [14] | 李永刚, 赵春风, 徐国元.信号去噪阈值与阈值函数的取舍研究[J]. 低温建筑技术,2010 (7):46–48. |
| [15] | WU Z H, HUANG E. Ensemble empirical modedecom position anoise assisted data analysis method[R]. Calverton: Center for Ocean-Land-Atmosphere Studies, 2005. |
| [16] |
IYAMA J, KUWAMURA H. Applicaton of wavelets to analysis and simulation of earthquakemtion motion[J].
Earthquake Engineering and Structural Dynamic, 1999,28 (2):255–272. |
| [17] | 赵建平, 徐国元, 李永刚.基于小波变换的爆破振动信号分解与重构[J]. 江西有色金属,2007 (2):11–14. |
| [18] | 张军华, 藏胜涛, 周振晓, 等.地震资料信噪比定量计算及方法比较[J]. 石油地球物理勘探,2009 (4):481–486. |
 2016, Vol. 7
2016, Vol. 7


