| 充填体下水平矿柱影响因素和安全厚度模拟分析 |
水平矿柱失稳的发生大致可以归结于地质与工程开挖条件. 矿柱岩体的性质,特别是矿柱岩体的抗压拉强度对矿柱稳定性起主要作用. 当矿岩节理裂隙发育,则应当是节理或破损矿岩的抗拉强度[1]. 当岩石呈厚块状、纯质、高强度时,倾角平缓,对矿柱稳定性有利,特别是地下水对矿岩的弱化作用,对矿柱稳定性也有较大影响. 地质构造对矿柱稳定性的影响主要表现在以下方面:破坏岩体完整性及连续性,形成各种岩体构造,弱化岩体强度. 地质构造对矿柱的稳定性都是不利的影响,查明矿区的地质构造特点对矿柱稳定性相当重要[2]. 原岩应力、由构造运动形成的构造应力对矿柱稳定性的影响,由于构造应力的大小和方向在不同的区域不相同,有的地区地质构造不发育,构造应力在开采中释放,对矿柱稳定性影响较小[3]. 矿体开采深度也是通过应力对矿柱稳定产生影响,随着开采深度的增加,在较深的井下产生高应力,在矿体开挖的过程中,破坏了应力平衡,致使矿柱较易破坏[4-5]. 上部充填体的重力、下滑、软化、稳定性是充填体下开采的重要特性. 充填体的自撑能力是由充填体自重、与围岩帮壁的摩擦阻力、岩移、充填及支护条件和爆破损伤等综合作用力形成的结果. 而充填体不接顶,导致下部充填体对留设的隔离结构没有起到支撑作用,由此上部的隔离结构容易破坏,形成贯通的充填体荷载,对下部留设的矿柱稳定性影响极大[6]. 因此,提高充填体接顶程度,是研究充填体对控制矿柱稳固的关键技术. 爆破震动效益是一个很复杂的问题. 循环加载的动荷载,对矿柱及充填体的破坏存在叠加效益.其存在对充填体的距离效应;对不同龄期充填体的影响;装药结构对矿柱及充填体的影响. 而采场的结构参数对矿柱的稳定性影响也很大,尤其是采场的暴露面积,暴露面积越大,采场越不稳定.
1 基于AHP的充填体下水平矿柱稳定性影响因素综合分析 1.1 构造层次结构分析模型充填体下水平矿柱稳定性受回采参数、地质条件和工程条件的综合影响,各因素间存在各种联系,各因素所占权重也各不相同,有些因素不能作定量化,造成这些因素的变化与充填体下水平矿柱稳定性之间也不存在明确的数学函数关系,不能建立明确的数学模型进行评价[7-8],故此,文中建立层次结构模型进行分析. 构建其影响因素综合评价层次体系,见表 1.
| 表1 充填体下水平矿柱稳定性影响因素综合评价体系 Table 1 Comprehensive evaluation system of stability of level under pillar filling body |
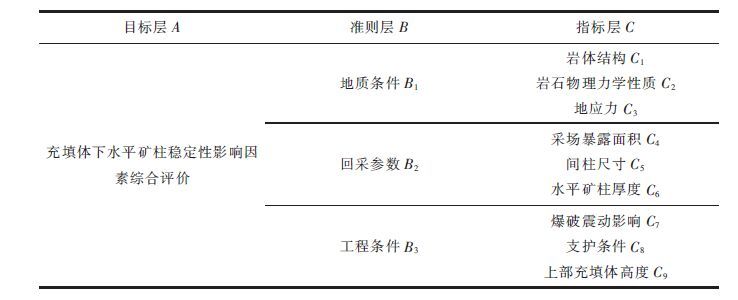 |
| 点击放大 |
1.2 构造判断矩阵
根据心理学研究和大量社会统计数据,引入Saaty等学者研究确定的9阶标度法,表 2评判各因素的相对重要性,建立各层因素两两判断矩阵. 构造判断矩阵是层次分析法的基础,判断结果由相关行业专家给出的综合评价决定.
| 表2 AHP评价尺度 Table 2 AHP evaluation |
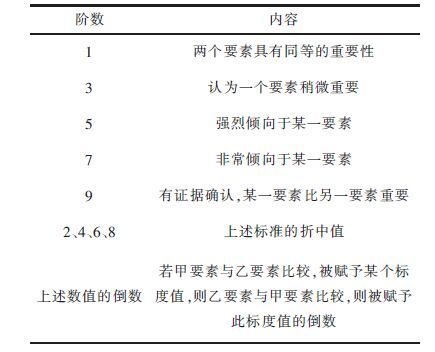 |
| 点击放大 |
分析各层要素重要性,构建判断矩阵A-B、B1-C、B2-C、B3-C如表 3~表 6所示.
| 表3 判断矩阵A-B Table 3 Judgment matrix A - B |
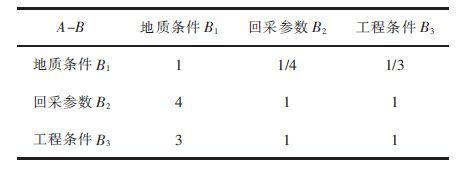 |
| 点击放大 |
| 表4 判断矩阵B1-C Table 4 Judgment matrix B1-C |
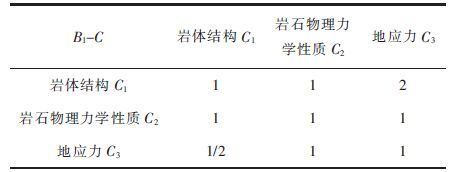 |
| 点击放大 |
| 表5 判断矩阵B2-C Table 5 Judgment matrix B2-C |
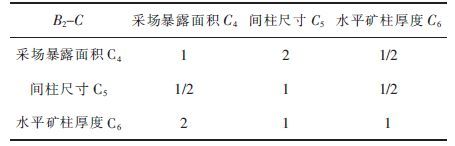 |
| 点击放大 |
| 表6 判断矩阵B3-C Table 6 Judgment matrix B3-C |
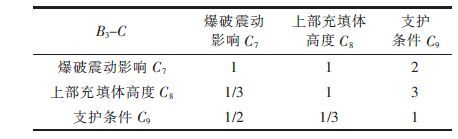 |
| 点击放大 |
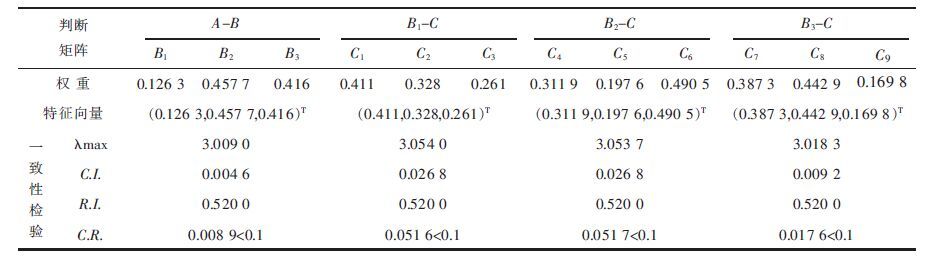
求解上述判断矩阵,可得判断矩阵的特征向量、要素在目标层所占权重及一致性检验指标计算结果,如表 7所示.
| 表7 判断矩阵计算结果 Table 7 Calculation results of judgment matrix |
 |
| 点击放大 |
1.3 判断矩阵的一致性检验
为了了解判断矩阵是否具有满意一致性,还需引入判断矩阵的一致性指标C.I.和随机一致性指标R.I.其具体数值见表 8.
| 表8 随机一致性指标 Table 8 Random consistency index |
 |
| 点击放大 |
| $C.I.=\frac{{{\lambda }_{\max }}-n}{n-1}$ |
| $C.R.=\frac{C.I.}{R.I.}$ |
根据公式计算判断矩阵的一致性比例C.R.,在C.R.=0时,称A是完全一致性矩阵;在C.R.<0.1时,则可以称判断矩阵A的一致性较好;在C.R.>0.1时,则A不具有一致性,需要重新调整判断矩阵[9].文中判断矩阵的一致性检验结果见相应矩阵的下方.
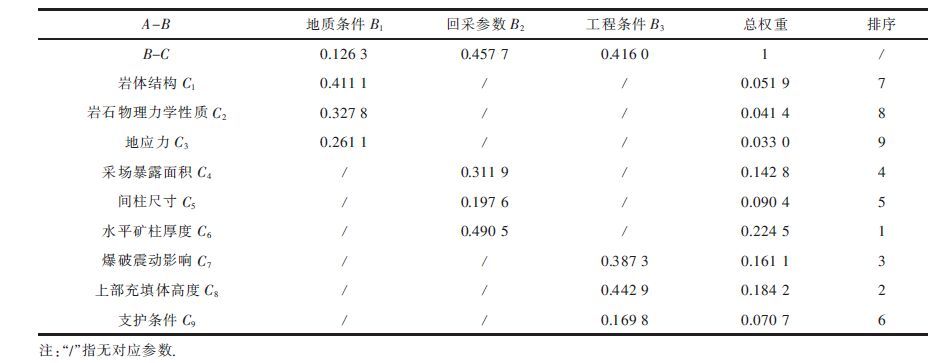
汇总得到充填体下影响水平矿柱稳定性的因素层次分析总权重排序(表 9).
| 表9 层次分析总权重排序 Table 9 Analytic hierarchy total weight sorting |
 |
| 点击放大 |
2 基于薄板理论的水平矿柱稳定性分析 2.1 预留安全厚度理论
通过对水平矿柱的受力分析及其赋存条件,将单个水平矿柱下部回采单元回采后简化为四边固支薄板[10],设矿柱宽为a,长为b,厚度为h.薄板上荷载为q,受力示意图见图 1.
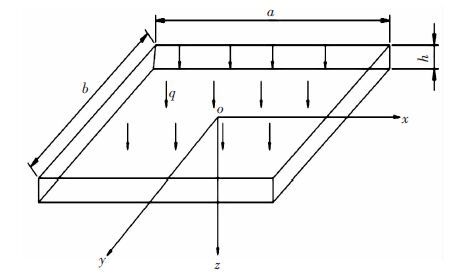 |
| 图 1 薄板尺寸及荷载分布 Fig. 1 Sheet size and load distribution |
薄板的挠度曲线方程为:
| $\omega =\frac{q{{a}^{4}}{{b}^{4}}}{D{{\pi }^{4}}\left( 3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}} \right)}{{\sin }^{2}}\frac{\pi y}{a}{{\sin }^{2}}\frac{\pi y}{a}$ | (1) |
式(1) 中:q为薄板面上均布荷载,板抗弯刚度
根据弹塑性理论,可得到薄板内应力与挠度的关系为:
| $\left. \begin{align} & {{\sigma }_{x}}=\frac{Ez}{1-{{\upsilon }^{2}}}\left( \frac{{{\partial }^{2}}\omega }{\partial {{x}^{2}}}+\upsilon \frac{{{\partial }^{2}}\omega }{\partial {{y}^{2}}} \right) \\ & {{\sigma }_{y}}=\frac{Ez}{1-{{\upsilon }^{2}}}\left( \frac{{{\partial }^{2}}\omega }{\partial {{y}^{2}}}+\upsilon \frac{{{\partial }^{2}}\omega }{\partial {{x}^{2}}} \right) \\ & {{\tau }_{xy}}=\frac{Ez}{1-{{\upsilon }^{2}}}\frac{{{\partial }^{2}}\omega }{\partial x\partial y} \\ \end{align} \right\}$ | (2) |
水平矿柱失稳破坏模式,由于矿岩的抗拉强度明显小于其他破坏强度,所以矿柱最可能出现的破坏模式为拉伸破坏[11].矿柱失稳破坏判据为当矿柱岩体的抗拉强度小于其受到的拉应力时,则矿柱出现拉伸破坏.
| $\max \left\{ {{\sigma }_{x}},{{\sigma }_{y}} \right\}>{{\sigma }_{t}}$ |
由薄板应力分布特点可知,在
| $\left. \begin{align} & \frac{{{\partial }^{2}}\omega }{\partial {{x}^{2}}}=\frac{2{{q}_{0}}{{a}^{4}}{{b}^{4}}}{{{a}^{2}}{{\pi }^{2}}\left( 3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}} \right)}{{\sin }^{2}}\frac{\pi y}{b}\cos \frac{2\pi x}{a} \\ & \frac{{{\partial }^{2}}\omega }{\partial {{y}^{2}}}=\frac{2{{q}_{0}}{{a}^{4}}{{b}^{4}}}{{{b}^{2}}{{\pi }^{2}}\left( 3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}} \right)}{{\sin }^{2}}\frac{\pi y}{a}\cos \frac{2\pi x}{b} \\ \end{align} \right\}$ | (3) |
将求得的二阶偏导数式(3) 代入应力分量表达式(2) ,得:
| $\left. \begin{align} & {{\sigma }_{x}}=\frac{-Ez}{1-{{\upsilon }^{2}}}\times \frac{2{{q}_{0}}{{a}^{4}}{{b}^{4}}}{{{a}^{2}}{{\pi }^{2}}\left( 3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}} \right)}{{\sin }^{2}}\frac{\pi y}{b}\cos \frac{2\pi x}{a} \\ & {{\sigma }_{y}}=\frac{-Ez}{1-{{\upsilon }^{2}}}\times \frac{2{{q}_{0}}{{a}^{4}}{{b}^{4}}}{{{b}^{2}}{{\pi }^{2}}\left( 3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}} \right)}{{\sin }^{2}}\frac{\pi y}{a}\cos \frac{2\pi x}{b} \\ \end{align} \right\}$ | (4) |
取
| ${{\sigma }_{\max }}=\frac{E{{q}_{0}}h}{1-{{\upsilon }^{2}}}\times \frac{2{{q}_{0}}{{a}^{4}}{{b}^{4}}}{D{{\pi }^{2}}\left( 3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}} \right)}\left( \frac{\upsilon }{{{a}^{2}}}+\frac{1}{{{b}^{2}}} \right)$ | (5) |
根据极限平衡理论,充填体荷载下水平矿柱最小厚度h为:
| $h=\sqrt{\frac{12{{q}_{0}}}{{{\pi }^{2}}\left[ {{\sigma }_{t}} \right]}\times \frac{{{a}^{4}}{{b}^{4}}}{3{{a}^{4}}+3{{b}^{4}}+2{{a}^{2}}{{b}^{2}}}\left( \frac{\upsilon }{{{a}^{2}}}+\frac{1}{{{b}^{2}}} \right)}$ | (6) |
江西东乡某铜矿-235 m中段至-280 m中段,水平矿柱上部有高度为H=45 m的胶结充填体,其密度为1 740 kg/m3,矿块宽25 m,矿房与矿柱各宽12.5 m,间柱为4 m,矿体平均厚度为15 m,矿体倾角为45°,回采单元长度为25 m.
岩体的极限抗拉强度为实验室得出经过折减的抗拉强度值,将参数a=15 m,b=25 m,泊松比v=0.25,抗拉强度σt=4.7 MPa,q0=γH=0.77 MPa代入式(6) 得水平矿柱的最小安全厚度为:3.45 m.考虑到矿区岩体较破碎,在上述暴露面积下回采矿体,而且可能会出现回采单元临近单元也同时开采的情况,回采单元相互影响,出于安全的考虑取1.5倍,水平矿柱所需留设的厚度最小为5 m.
3 水平矿柱稳定性数值模拟 3.1 建立数值模型针对采矿工程问题模拟分析,采场回采对周围3~5倍的围岩会产生影响,围岩所选取的尺寸为采场高度、宽度和长度的3~5倍[12-13].在ANSYS中建立模型,以垂直矿体走向为X轴,沿矿体走向为Y轴.模型分别建立上下盘围岩和矿体,模型尺寸为250 m×250 m×200 m(X×Y×Z),模型上部到地表的距离为225 m.矿体网格采用8节点单元,先对构成模型的各条线划分,然后sweep网格划分,划分网格后,利用接口程序将之导入FLAC3D中生成最终计算的数值模型[14],模型单元数为323 544个,节点数为342 063个,模型如图 2所示.
 |
| 图 2 ANSYS转入FLAC3D的整体模型 Fig. 2 ANSYS to FLAC3D model |
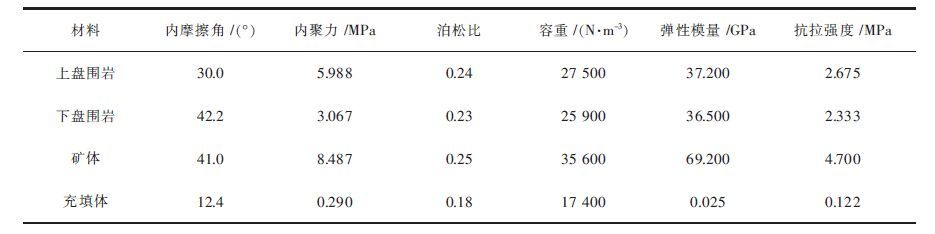
根据经验类比,上盘岩体与下盘岩体较破碎,上盘岩体、下盘岩体、矿体的折减系数分别为1/8,1/9,1/7,充填体不折减.并利用弹性模量和泊松比求出体积模量和切变模量[15],具体参数见表 10.
| 表10 计算模型材料力学参数 Table 10 Calculation model for material mechanics parameters |
 |
| 点击放大 |
3.2 设计方案
在回采矿房时,最危险的情况就是在上阶段为充填体,回采下部回采单元的时候,临近回采单元同时也在开采.水平矿柱分别取5 m,6 m,7 m,8 m,9 m,设置3个采矿单元,回采步骤为同时回采上阶段回采矿房1至矿房3,回采矿柱1至矿柱3,充填回采单元1至回采单元3;此时下阶段回采单元上部即为充填体,留设水平矿柱保证上部充填体的稳定,回采下阶段回采矿房4至矿房6,回采矿柱4至矿柱6,充填回采单元4至回采单元6.故此次数值模拟试验的回采单元设计见图 3.
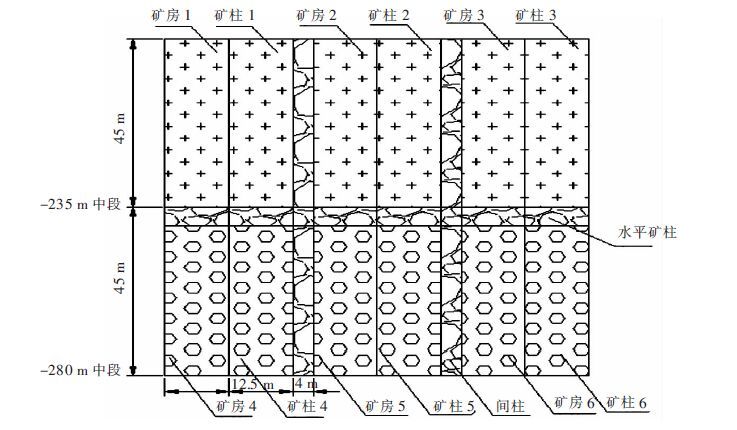 |
| 图 3 回采单元分布示意 Fig. 3 Extraction unit distribution |
3.3 模拟结果分析 3.3.1 应力分析
在图 4(a)~(j)中,下阶段回采单元开采结束后,水平矿柱受到沿z轴负方向的最大主应力,最大主应力由水平矿柱中心向两侧呈放射形逐渐增大,并在间柱内部出现应力集中,留5~9 m矿柱最大主应力峰值依次为37.67 MPa、37.56 MPa、37.15 MPa、36.49 MPa、35.66 MPa,都大于岩体的抗拉强度(33MPa),间柱内部破坏. 随着矿柱厚度的增加,间柱的破坏面积越来越小,由于最大主应力的分布受水平矿柱角度倾向影响,沿倾角方向逐渐增大.
同时,水平矿柱中心区域受沿z轴正方向的剪应力,留5~9 m矿柱剪应力最大值峰值依次为3.03 MPa、3.15 MPa、3.27 MPa、3.02 MPa、2.83 MPa.剪应力沿阶段矿柱的中心区域向两侧呈类椭圆状放射形减小,在间柱与水平矿柱相交面的中心出现剪应力集中,方向为沿z轴负方向,留5~9 m矿柱两侧面剪应力最大值依次为-9.89 MPa、-10.04 MPa、-9.95 MPa、-9.72 MPa、-9.32 MPa.
无论是最大主应力,还是剪应力,都随着阶段矿柱的厚度增加,而应力集中越小.所以要保证阶段矿柱的稳定性,留设足够厚的矿柱是必要的.
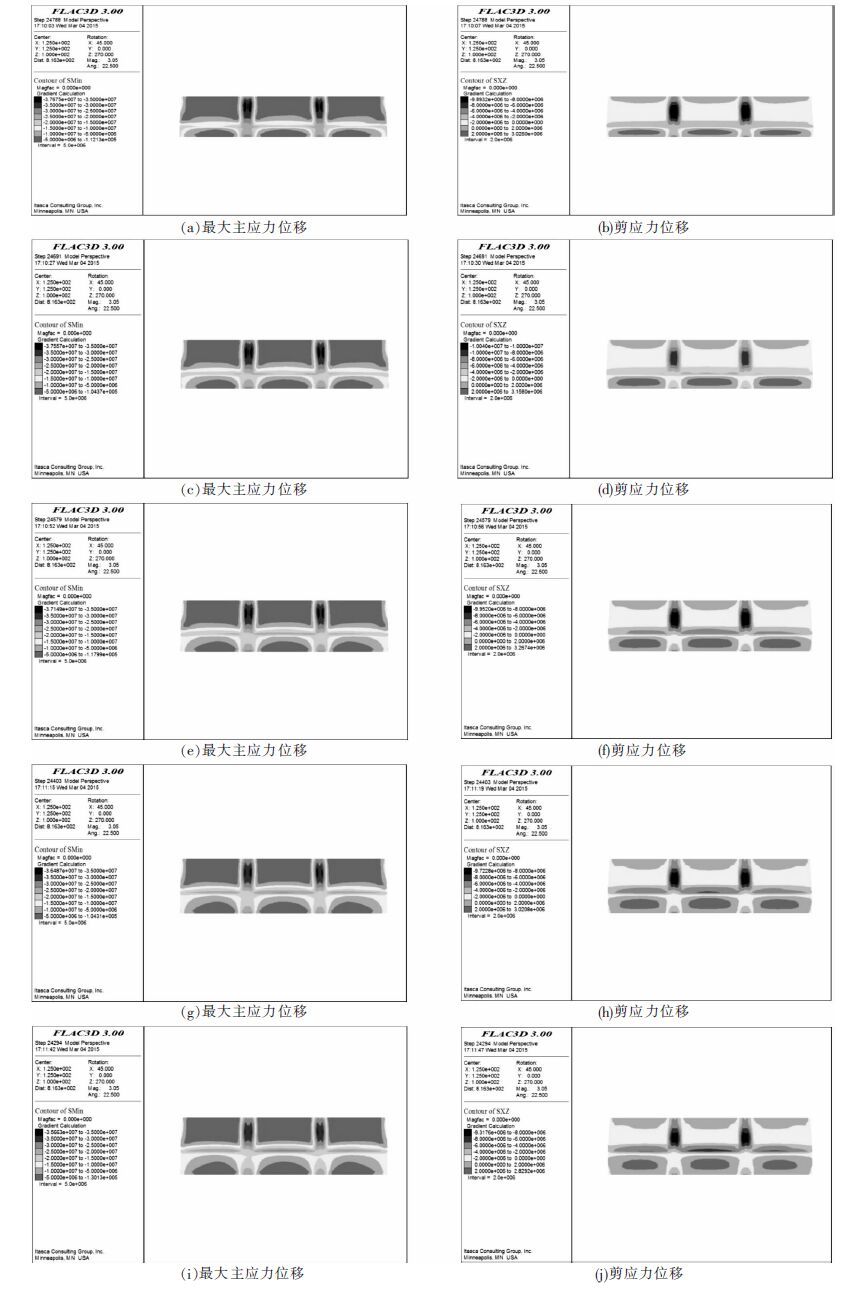 |
| 图 4 5~9 m水平矿柱最大主应力与剪应力位移云图 Fig. 4 Maximum principal stress and shear stress displacement of 5~9 m horizontal pillar |
3.3.2 位移分析
如图 5所示,水平矿柱中心区域的垂直位移峰值明显大于两侧,位移方向为沿z轴负方向.随着水平矿柱厚度的增加,水平矿柱稳定性增加,中心区域z方向峰值逐渐减小,但水平矿柱两侧垂直位移峰值变化不大. 5~9 m水平矿柱的垂直位移峰值依次为 -46.33 mm、-44.99 mm、-43.63 mm、-42.29 mm、 -41.10 mm.由于变形较大,在连续回采单元时要做好位移监测工作.
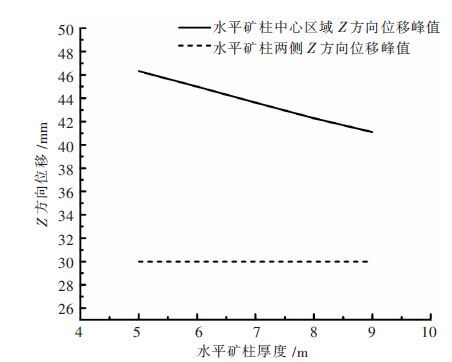 |
| 图 5 水平矿柱垂直位移与水平矿柱厚度变化关系 Fig. 5 Variation diagram of horizontal pillar vertical displacement and horizontal pillar thickness |
3.3.3 塑性区分析
矿体开采产生的塑性区主要分布在矿柱表面,当水平矿柱为5 m、6 m时,水平矿柱内部均有大面积塑性区贯通,并且有很多塑性区破坏正在发展,水平矿柱完全破坏.当水平矿柱为8、9 m时,虽然表面有大量塑性区,但内部只在1~3 m的区域出现塑性区,水平矿柱中心5 m以上范围内均无塑性区,水平矿柱非常稳固.作为塑性区出现的分水岭,7 m水平矿柱表面出现大面积塑性区,内部塑性区分布较少,且在中心区域有3 m范围内未出现塑性区,塑性区未发生贯通,水平矿柱的稳定性较好,如图 6所示. 不同方案的塑性区体积如图 7,不同厚度的水平矿柱的塑性区体积虽有波动,但其体积比却一直是在减小的. 7 m矿柱的塑性区体积开始减少,8 m的塑性区体积和7 m相差无几;9 m的拉伸塑性区增加了一点,但所占总体积的百分数还是减小的.
 |
| 图 6 7 m水平矿柱塑性区分布 Fig. 6 7 m level pillar plastic layout |
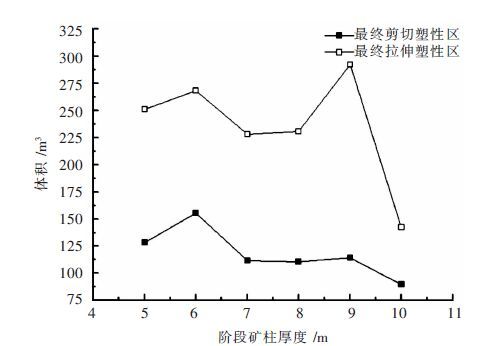 |
| 图 7 塑性区体积 Fig. 7 Plastic zone size |
4 结 论
1)通过因素总排序,回采参数和工程条件对充填体下水平矿柱稳定性影响较大,故而在采场设计时需加以重视.从指标层中,可以进一步看出水平矿柱厚度在准则层的回采参数中权重较高;岩体结构在准则层的地质条件中权重较高;爆破震动、上部充填体高度在准则层的工程条件中权重较高.岩体结构是自然条件决定的,而采场暴露面积、水平矿柱厚度、爆破震动是可控的,在开采矿体时,需予以重视.特别要注意的是上部大面积的充填体对水平矿柱稳性的影响.
2)应用小变形薄板理论公式计算出在充填体下留设水平矿柱的最小安全厚度为5 m. 并以此作为建立数值模型的基础,利用FLAC3D软件模拟先回采上部单元,嗣后充填,以及在充填体下回采下部矿体的过程. 模拟中留设不同厚度水平矿柱,分析水平矿柱厚度为5 m至9 m时应力、垂直位移及塑性区分布,从而判断其稳定性. 结果表明:5 m、6 m厚的矿柱稳定性不够,8 m、9 m的矿柱又会造成很大的损失率,最终确定在采场宽度为15 m,回采单元长为25 m,暴露面积为375 m2时,水平矿柱厚度为7 m符合要求.
| [1] | 李其昌. 金阳公路保安矿柱开采技术研究[D].长沙:中南大学,2004. http://cdmd.cnki.com.cn/article/cdmd-10533-2004093624.htm |
| [2] | 罗小新, 马玄恒, 黄晓毅.隔离矿柱合理参数的研究[J]. 重型机械,2010 (增2):109–113. |
| [3] | 宋华. 建筑物下保安矿柱回采地压分布规律与控制研究[D].武汉:武汉理工大学,2013. http://cdmd.cnki.com.cn/article/cdmd-10497-1013296131.htm |
| [4] |
ZHOU J, LI X B, SHI X Z. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods[J].
Transactions of Nonferrous Metals Society of China, 2011 (12):2734–2743. |
| [5] |
LIU Z X, DANG W G, HE X Q. Cancelling ore pillars in large-scale coastal gold deposit: A case study in Sanshandao gold mine, China[J].
Transactions of Nonferrous Metals Society of China, 2013 (10):3046–3054. |
| [6] | 董凯程, 吴春平, 冯盼学.充填体下水平矿柱开采技术研究[J]. 中国矿业,2012 (9):103–105. |
| [7] |
HU Y X, LI X B. Bayes discriminant analysis method to identify risky of complicated goaf in mines and its application[J].
Transactions of Nonferrous Metals Society of China, 2012 (2):425–431. |
| [8] | 张炳江. 层次分析法及其应用案例[M]. 北京: 电子工业出版社 , 2014 . |
| [9] | 李伯德. AHP判断矩阵一致性改进方法研究[D].兰州:兰州大学,2007. http://cdmd.cnki.com.cn/article/cdmd-10730-2008019065.htm |
| [10] | 唐晓玲, 叶明亮.薄煤层坚硬顶板的薄板理论分析及来压预报[J]. 矿山压力与顶板管理,2003,20 (2):89–92. |
| [11] | 刘波. 复杂条件下水平矿柱稳定性分析及其开采方案研究[D].赣州:江西理工大学,2013. http://cdmd.cnki.com.cn/article/cdmd-10407-1014102035.htm |
| [12] | 黄敏. 铜绿山矿充填体下残矿回采关键参数数值模拟优化研究[D].长沙:中南大学,2012. http://cdmd.cnki.com.cn/article/cdmd-10533-1012477520.htm |
| [13] | 谢晓斌. 龙门山矿区L-23矿体上行式开采技术研究[D].赣州:江西理工大学,2012. http://cdmd.cnki.com.cn/article/cdmd-10407-1012507226.htm |
| [14] | 陈育民. FLAC及FLAC3D基础与工程实例[M]. 北京: 水利水电出版社 , 2013 . |
| [15] | 蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社 , 2009 . |
 2016, Vol. 7
2016, Vol. 7


