| 电磁搅拌下稀土在铝合金熔体中的分布规律 |
b. 江西理工大学, 材料科学与工程学院,江西 赣州 341000
b. School of Material Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
金属在熔融状态时其流动状态及其内部成分的分布对凝固过程会产生非常大的影响,熔体内部的对流将直接影响凝固过程中的传热及传质过程,因此金属熔融状态下的流动状态决定了其凝固组织和成分分布[1]. 在金属熔体流动时,为了促进其内部温度及物质的均匀分布,对其施加力场是十分必要的,即通过各种外力的作用增加金属熔体内的对流扩散效果能够极大地提高其温度及物质的混合效率. 并在实践生产过程中发现,电磁搅拌(Electromagnetic stirring:EMS)不仅能对金属熔体具有搅拌作用,一定的电磁频率下还能对金属的性能产生影响[2-3]. 电磁场应用于冶金生产的发展过程可大致分为孕育期、开始应用期及发展期这3个阶段[4]. 从19世纪初的法国学者Faraday对地磁场与海水运动关系的研究到1932年布劳贝克发现在旋转电磁场的作用下可以使得流体流动,以及后来经过法国学者Alfven的长期研究工作,奠定了磁流体力学(Magneto Hydrodynamics,简称MHD)的基础. 从20世纪40年代起,磁流体动力学就开始应用于冶金工业生产中,进入了MHD在冶金生产中的应用期,并由于电磁场的非直接接触、便于实现自动控制、降低成本等因素,逐步进入到发展阶段[4]. 由于电磁搅拌具有非接触和无污染等优点,对于铝合金熔体的凝固过程来说,对其施加一个电磁场,利用铝合金熔体所受到的电磁力对铝熔体进行搅拌,调制铝合金的凝固过程,实现改善铝合金的凝固组织与性能.
铝在国民经济和国防建设中应用十分广泛,而在铝熔体中加入适量的稀土形成的稀土铝合金的性能大大提高[5-9],更利于铝的广泛应用.应用电磁搅拌能够有效减少稀土铝合金产品中的杂质,提升产品的质量,可为铝合金的半固态制备工艺提供可靠的技术保证.由于电磁场作用下铝合金熔体呈现紊流甚至混沌状态[10],通过应用Fluent软件进行流体模拟仿真[11-18],可以较好地探明和反映其中的规律与特征.因此,本研究将针对铝-稀土多相熔体在电磁搅拌过程中的流动状态,并以A356-La合金为对象,结合铝合金半固态制备工艺,应用Fluent软件的计算功能,研究电磁搅拌下A356-La熔体中稀土扩散与分布的规律.
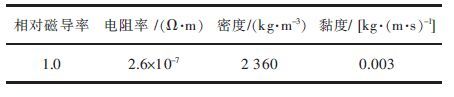
1 模型建立 1.1 实 验实验所用A356铝合金经Magix (PW2424) X荧光光谱仪分析,其实际成分(质量分数)为:0.33 Mg,7.1 Si,其余为Al,表 1为其主要参数[4].
| 表1 A356主要参数 Table 1 Major parameters of A356 |
 |
| 点击放大 |
将A356铝合金炉料投入预热到300 ℃的石墨坩埚,在SG2-3-10坩埚式电阻炉中进行熔炼,熔化过程中,加入覆盖剂(50 %的NaCl)进行覆盖,形成熔池后表面除渣,将炉温缓慢升温至720 ℃,分2~3次除气精炼. 精炼结束静止1~2 min,再将炉温升至780 ℃,加入预先配置好的Al-50 %La中间合金,保温10 min后,将铝合金-稀土熔体逐步降温至640 ℃(接近液相线温度附近),采用低过热度浇注和电磁搅拌制备半固态A356-La合金浆料. 将合金熔体浇注到底面直径d=60 mm,高度h=100 mm,壁厚s=2.0 mm的不锈钢搅拌坩埚中,启动电磁搅拌器以不同的电磁频率(f=5 Hz、15 Hz和30 Hz)对铝合金熔体搅拌若干秒钟.然后,迅速将坩埚浸入水中进行水淬,最终获得A356-1.2 %La合金铸锭.
本研究所用电磁搅拌器如图 1所示.
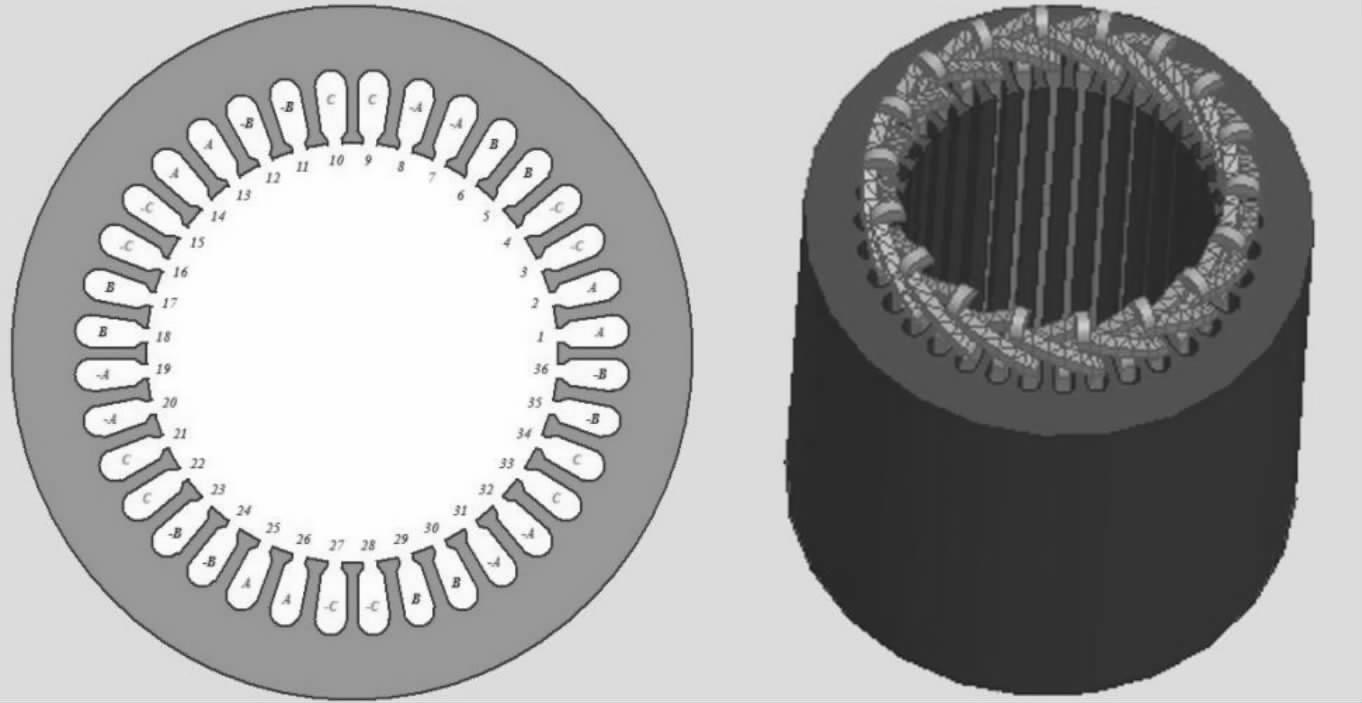 |
| 图 1 电磁搅拌器相位及实体示意 Fig. 1 Phase diagram and solid diagram of electromagnetic stirrer |
1.2 物理模型
为了便于模拟,在本研究中假定铝-稀土(A356-La)多相熔体是不可压缩的导电流体,且其在温度变化的过程中密度、黏度、导电率等相应的物理化学性质及参数均恒为定值;设铝-稀土多相熔体的磁导率为真空磁导率(μ0=4π×10-7 H/m),且在低频电磁搅拌过程中,铝合金熔体始终处于液态,无凝固组织析出;此外,铝-稀土多相熔体的流速较小,其对磁场的影响较小而忽略不计;将坩埚视作为一个圆柱体进行分析.
为了提高模拟效率,本研究对坩埚进行了简化,其网格图如图 2所示.
 |
| 图 2 铝-稀土多相熔体网格 Fig. 2 Grid of aluminum and rare earth multiphase melt |
1.3 电磁场模型
本研究所用电磁场为旋转电磁场,在未考虑电位移的情况下(电位移D=0) ,坩埚内铝-稀土多相熔体中电磁场分布情况可由Maxwell方程组[式(1) ,式(2) ,式(3) ]求解所得.
| $J=\nabla \times H$ | (1) |
| $\frac{\partial B}{\partial t}=\nabla \times E$ | (2) |
| $\nabla \times B=0$ | (3) |
其中:J为自由电流面密度;H为磁场强度;B为磁感应强度;E为电场强度;t为时间.铝-稀土多相熔体在电磁场中所受洛伦兹力可由式(4) 求解得:
| $F=J\times B$ | (4) |
将熔体视为不可压缩的理想状态流体,即认定其搅拌过程中始终为连续状态,其连续方程为:
| $\nabla \times u=0$ | (5) |
搅拌过程中,流体流动情况复杂,适宜非定常流模型分析,故选用标准k-ε方程模型. 研究对象为不可压缩流体且不考虑其它源项情况时,标准k-ε模型方程如下:
| $\rho \frac{Dk}{Dt}=\frac{\partial }{\partial {{x}_{i}}}\left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{i}}} \right]+{{G}_{k}}-\rho \varepsilon $ | (6) |
| $\rho \frac{D\varepsilon }{Dt}=\frac{\partial }{\partial {{x}_{i}}}\left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{i}}} \right]+{{C}_{1z}}\frac{\varepsilon }{k}{{G}_{k}}-{{C}_{2z}}\rho \frac{{{\varepsilon }^{2}}}{k}$ | (7) |
其中:k为湍动能;ε为耗散率;μ为黏性系数;μt为湍流黏性系数;根据Launder等学者推荐可选取常数C1z=1.44,C2z=1.92;Gk表示由于平均速度梯度引起的湍动能产生.
由于本研究中涉及到铝合金熔体及稀土合金,包含了两相流体,所以选取多应用于上浮、颗粒悬浮以及流化床等情形的Eulerian模型.
2 模拟结果 2.1 电磁场的模拟结果利用Ansoft Maxwell软件对搅拌器进行2D建模,并对不同频率条件下电磁搅拌器中铝-稀土多相熔体所处电磁场中的电磁感觉强度进行仿真分析.忽略电磁搅拌器两端以及气隙对电磁场的影响,电磁搅拌器中径向电磁感应强度沿着其轴向变化不大,故可选取其横截面进行磁感应强度分析.搅拌器工作时额定电压U=380 V、额定转速n=960 r/min、额定功率P=1.5 kW,内含3对电极、36组定子绕组,选取时间t=0.3 s时,电磁搅拌器在各频率下的横截面电磁感应强度云图如图 3所示.
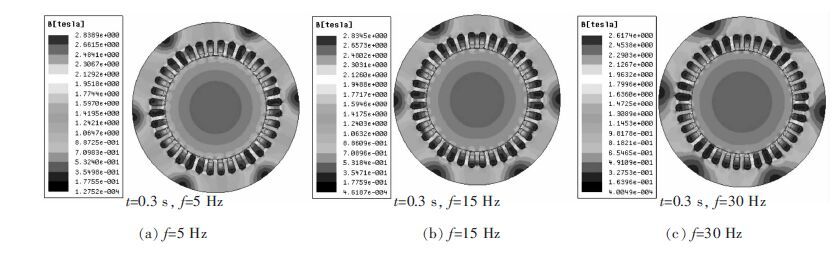 |
| 图 3 各频率下电磁搅拌器的感应强度云图 Fig. 3 Induction intensity images of electromagnetic stirrer under different frequencies |
由图 3可知电磁搅拌器中的电磁场强度分布具有规律性,以各个电极为电磁强度核心,整个电磁场可划分为6个电磁强度分布状态相同的扇形.电磁强度从定子绕组半径方向向圆心阶梯式递减,由于存在气隙的影响,电磁强度在半径方向经过一个快速减弱区域后保持相对稳定.
2.2 流场的模拟结果在不同频率的电磁场中,利用Fluent软件对所建立的流场模型进行仿真分析,对在各个频率下稀土La经过电磁搅拌后在流场中的分布情况进行3D建模分析.取模型竖直方向截面,假设铝合金熔体在电磁场搅拌之前处于静止状态,且由于稀土密度较铝合金的更大,因此在电磁搅拌之前铝合金熔体中稀土的分布情况云图如图 4所示,并取此刻为电磁搅拌时间t=0时.
当搅拌频率f =5 Hz时,不同搅拌时间下稀土在铝合金熔体中的分布情况如图 5所示.
 |
| 图 4 稀土La分布云图(未搅拌) Fig. 4 Distribution image of La (without stirring) |
 |
| 图 5 稀土La分布云图(f=5 Hz) Fig. 5 Distribution images of La (f = 5 Hz) |
此时,由于电磁频率低,在铝合金熔体中产生的Lorentz力较小,对铝合金熔体引起的扰动也较小,坩埚内稀土最高浓度随着搅拌时间增长而慢慢降低,5 s时为53.6 %、15 s时为12.1 %、至20 s降至9.08 %;同时其最低浓度呈增长状态,由5 s时接近0慢慢增加至20 s的0.272 %,并且整个坩埚中稀土分布通过底面以及壁面逐渐向坩埚中上部扩散,在20 s时稀土分布呈现水瓶状. 整个搅拌过程中,随着时间的推移,坩埚内稀土分布更加均匀.
当搅拌频率f=15 Hz时,不同搅拌时间下稀土在铝合金熔体中的分布情况如图 6所示. 此时,由于电磁频率的上升,搅拌力的增大,导致溶质扩散逐渐加快. 随着搅拌时间的增长,坩埚内部稀土最高浓度快速地从5 s时的51.4 %降低至15 s时的5.45 %,至20 s时降为4.05 %;同时最低浓度也由5 s时近似为0快速增长至20 s时的0.6 %;稀土扩散轨迹仍沿着底面及壁面逐渐向坩埚中上部开始扩散,且随着时间的推移,坩埚内稀土分布更为均匀.
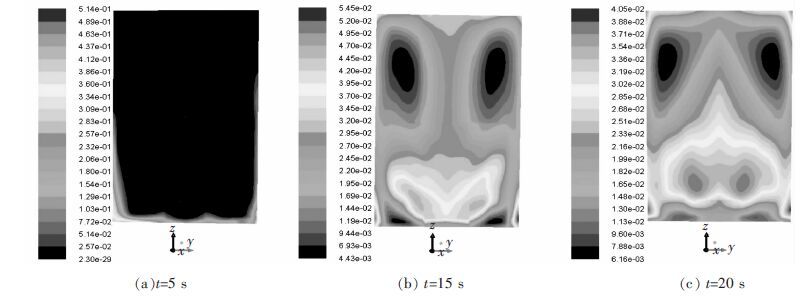 |
| 图 6 稀土La的分布云图(f=15 Hz) Fig. 6 Distribution images of La (f=15 Hz) |
当搅拌频率f=30 Hz时,不同搅拌时间下稀土在铝合金熔体中的分布情况如图 7所示. 此时,由于电磁频率进一步升高,铝合金熔体中产生的Lorentz力增大,溶质扩散的驱动力亦增大. 当搅拌时间延长时,坩埚内稀土最高浓度由5 s时50.5 %降至15 s时7.55 %,至20 s时为6.28 %;同时最低浓度也由5 s时近似为0增长为20 s时0.514 %;稀土扩散轨迹由底面及壁面逐渐向坩埚中上部扩散,且随着时间的推移,渐渐向坩埚中心位置集中. 整个搅拌过程中,稀土分布随着时间的推移更为均匀.
对比图 5、图 6及图 7可知,相同搅拌时间内坩埚内稀土最高浓度及最低浓度差在一定范围内随着频率的增加而减少,当f=15 Hz时其浓度差最小;搅拌频率与搅拌时间达到一定数值时,容易引起稀土的局部偏析现象,但整个坩埚内的稀土分布随着搅拌频率与搅拌时间的增长而更趋向于均匀;搅拌频率的增加对稀土的扩散轨迹影响不大,只对其扩散速率造成影响.
 |
| 图 7 稀土La分布云图(f=30 Hz) Fig. 7 Distribution images of La (f = 30 Hz) |
3 结果与分析
在本实验中,搅拌时间为15 s时各搅拌频率下所得的金相组织如图 8所示.
由图 8可以看出,实施电磁搅拌,即使是在较低的电磁搅拌频率下(如5 Hz),A356-La铝合金的凝固组织发生了变化,粗大的枝晶由于受到电磁搅拌的作用被破碎,且逐渐形成了完整的蔷薇状枝晶,见图 8(a)所示. 随着电磁搅拌频率的增加,A356-La铝合金凝固组织中的粗大枝晶已经消失,枝晶数量明显减少,见图 8(b)所示. 当电磁搅拌频率增加至30 Hz,A356-La铝合金凝固组织中有大量颗粒的初生α相,而蔷薇状组织及枝状初生α相几乎不存在,晶粒更加圆整及均匀,见图 8(c)所示.
 |
| 图 8 不同搅拌频率下A356-La合金的凝固组织 Fig. 8 Microstructure of A356-La alloy at the different stirring frequencies |
通过实验研究可知,在施加电磁搅拌下,在A356-1.2 %La合金中能获得较细小圆整的初生相组织. 电磁搅拌影响凝固形貌的机制可以理解为熔体在凝固过程中,稀土元素La富集在固液界面前沿上,微观上影响了流动的熔体中固液界面原子的迁移,并阻碍了初生相的长大,使得结晶时潜热较难传出从而促使枝晶内部温度提高而熔断.由于La能拓宽合金的固液相区的宽度,且稀土元素的加入能起到变质作用,能使原本粗大的枝晶变成蔷薇状或球状.为了确定合金元素和稀土元素在合金组织中的分布情况,对加入稀土La和Yb的2个最优样品的亮白色物质组成分析,做SEM测试和EDS测试,结果如图 9所示.
1) 对比f=5 Hz、f=15 Hz、f=30 Hz时电磁搅拌对铝-稀土多相熔体的搅拌效果的影响最终得出:其他条件不变,在一定范围内,随着搅拌时间的增加,铝-稀土多相熔体的电磁搅拌效果越好.随着电磁搅拌频率增大,铝-稀土多相熔体的搅拌效果越均匀.在本模型中,稀土在电磁场作用下其扩散运动主要是从四周开始,随着时间的推移逐步向中心转移,因此容易在四周及中心位置形成高浓度区域.
2) 单一频率电磁搅拌在搅拌过程中的效果不是很好,且搅拌频率越低,搅拌坩埚内更易形成相对稳定的平衡区,随着搅拌时间的增加,搅拌效果将越来越差,因此对于提高电磁搅拌效果可考虑变频搅拌的方式.
3) 通过运用Ansoft和Fluent软件,采用磁场模型、Eular模型和k-ε模型对铝-稀土多相熔体在电磁搅拌下进行运动仿真,能够较好地得到电磁搅拌下铝-稀土多相熔体的混合效果,证实了该研究方案的可行性.
4) 半固态A356-1.2 %La铝合金经过较低频率电磁搅拌之后,对凝固组织具有细化作用,能获得较细小圆整的初生α相组织.
| [1] | 黄长虹, 徐益民, 张伟强.稳恒磁场中Al-4.5 %Cu合金热电磁流体动力学效应的数值模拟[J]. 热加工工艺,2008,37 (9):41–44. |
| [2] | 毛卫民, 甄子胜, 陈洪涛.电磁搅拌参数对半固态AZ91D镁合金组织的影响[J]. 特种铸造及有色合金,2005,25 (9):538–540. |
| [3] | 刘政, 谌庆春, 许鹤君, 等.稀土Y在电磁搅拌条件下对半固态ZL101铝合金初生α相的影响[J]. 有色金属科学与工程,2013,4 (6):92–98. |
| [4] | 黄军. 电磁搅拌作用下铝熔炼炉内多物理场耦合分析及工艺参数优化[D]. 长沙:中南大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10533-2010187648.htm |
| [5] |
OKAMOTO H. Al-Y (Aluminum-Yttrium)[J].
Journal of Phase Equilibria and Diffusion, 2008 (1):114. |
| [6] |
TSAI Y C, CHOU C Y, LEE S L, et al. Effect of trace La addition on the microstructures and mechanical properties of A356(Al-7Si-0.35Mg) aluminum alloys[J].
Journal of Alloys and Compounds, 2009 (1):157–162. |
| [7] |
VON?INA M, KORES S, MRVAR P, MEDVED J. Effect of Ce on solidification and mechanical properties of A360 alloy[J].
Journal of Alloys and Compounds, 2011,27 :7349–7355. |
| [8] | 刘政, 谌庆春, 郭颂.铝钇共晶反应及其产物对亚共晶铝硅合金初生相的细化研究[J]. 稀有金属,2013,37 (5):708–714. |
| [9] | 刘政, 谌庆春, 郭颂, 等.A356-RE合金中稀土铝化合物/初生α相界面二维错配度的计算及验证[J]. 稀有金属材料与工程,2015,44 (4):859–865. |
| [10] | 刘政, 张嘉艺, 邓可月.基于Fluent的电磁场中铝熔液及其质点运动轨迹的数值模拟[J]. 有色金属科学与工程,2015,6 (4):46–51. |
| [11] |
ZALE J M, SZALAI E S. Using CFD to understand chaotic mixing in laminar stirred tanks[J].
Aiche Journal, 2002,48 (10):2124–2134. DOI: 10.1002/(ISSN)1547-5905. |
| [12] |
PRASANTA K S, MULLICK A N. Computational investigation of performance characteristics in a C-shape diffusing duct[J].
International Journal of Advances in Engineering & Technology, 2013,3 (1):129–136. |
| [13] |
YANG W, WANG Y, CHEN J. Computation fluid dynamic simulation of fluid flow in a rotating packed bed[J].
Chemical Engineering Journal, 2010,156 :582–587. DOI: 10.1016/j.cej.2009.04.013. |
| [14] | 邱立杰, 张国福.基于FLUENT的弯管内部流场的数值模拟[J]. 辽宁石油化工大学学报,2013,33 (1):48–52. |
| [15] |
LAMBERTO D J, ALVAREZ M M. Computation analysis of regular and chaotic mixing in a stirred tank reactor[J].
Chemical Engineering Science, 2001,56 (16):4887–4899. DOI: 10.1016/S0009-2509(00)00407-3. |
| [16] | 王福军. 计算流体动力学[M]. 北京: 清华大学出版社 , 2004 . |
| [17] | 李荣, 冯永保.基于Fluent的电磁阀内部流场的三维仿真与分析[J]. 液压与气动,2013,10 (25):96–98. |
| [18] |
RANADA V V, RAMPURE M. Hydrodynamic of bubble column reactors at high gas velocity: experiments and computational fluid dynamics (CFD) simulations[J].
Industrial & Engineering Chemistry Research, 2007,46 (25):8431–8447. |
| [19] | 刘政, 黄美艳, 柯婷婷.稀土La对半固态A356初生α相细化机制的研究[J]. 有色金属科学与工程,2011,2 (5):24–28. |
| [20] |
LIU X M, LIU Z. Effect of eutectic reaction induced by La on microstructure in semisolid A356 alloy[J].
Advanced Materials Research, 2012,424/425 :77–80. DOI: 10.4028/www.scientific.net/AMR.424-425. |
 2016, Vol. 7
2016, Vol. 7


