| 海外矿山项目并购宏观经济风险评价 |
b. 江西理工大学矿业贸易与投资研究中心,江西 赣州 341000
b. Research Center of Mining Trade & Investment, Jiangxi University of Science and Technology, Ganzhou 341000, China
矿产资源是我国国民经济发展的基础,随着我国经济的快速发展以及工业化和城镇化进程的不断推进,对矿产资源的依赖程度不断加大.国内矿产资源早已难以满足国内市场的巨大需求.在2008年世界金融危机的影响下,全球矿产品市场价格大幅下跌,我国外汇储备不断增加、人民币不断升值,外国政府对投资政策制度的放宽,使得中国矿业企业的海外并购取得了较大的进展.据商务部有关统计数据显示,2008~2013年间,我国资源型企业并购海外矿业项目共成交91笔,成交总金额达319亿美元[1].仅2009年一年,我国的矿产及能源业海外并购交易总额就高达156.6亿美元,海外并购已成为我国资源型企业发展的重要途径.然而,据麦肯锡研究数据显示,在过去20多年里,在全球矿业企业并购案中能达到预期效果的不到50﹪,而中国则有70﹪的企业在海外并购过程中走向失败[2-3].伴随着“走出去”战略的不断深入,海外矿山项目并购面临的各类风险不断呈现,科学评价海外矿山项目并购的宏观经济风险,对于缓解我国矿产资源瓶颈和顺利实现我国资源型企业的国际化经营意义重大.
在并购风险评价方面,常用的评价方法有层次分析法、模糊综合法、灰色理论、BP神经网络、粗糙集理论等.在灰色理论和TOPSIS运用方面,付沙[4]将模糊集理论与灰色系统理论相结合,在对信息系统风险进行识别的基础上,构建了基于灰色模糊理论的信息系统安全风险评价模型,综合分析了多类风险因素对信息系统的影响.马运来[5]将TOPSIS与主成分分析法相结合,有效解决了投资环境的复杂性和多层次性问题,并以2004年我国各省市的相关数据为样本进行案例分析并提出对策,为改善投资环境风险提供了决策依据.张振辉[6]运用灰色关联分析来对多个海外并购方案的风险大小进行排序,并将评价结果与模糊综合评价法的评价结果进行对比,以确定并购的最佳方案.研究结果表明,将灰色关联分析法运用于企业并购风险识别方面效果显著.总体看来,将灰色关联理论与TOPSIS相结合来评价海外并购的宏观经济风险的研究相对较少,具有一定的研究价值.
TOPSIS法是以接近正理想解或远离负理想解的距离作为度量依据,它只能通过函数曲线来反映与数据曲线间的位置关系,无法体现出数据序列与各理想方案之间的态势变化[7].然而,海外矿山项目并购是一个多目标决策过程,指标数据较少且数据波动性较大,没有清晰的分布规律,因素之间的数量关系并不明确,这符合灰色系统的典型特征.运用灰色关联度理论,可以较好地分析风险态势的变化,有效衡量曲线形状的相似程度.曲线形状拟合程度越高,相应样本之间的关联度就越大[8-10].鉴于TOPSIS法中欧式距离和灰色关联度理论可以分别从位置和形状相似程度两个角度来反映备选方案与理想方案之间的拟合程度,故将二者结合起来,提出了一种基于理想解法和灰色关联度的海外矿山项目并购宏观经济风险评价方法,为多目标风险决策问题提供了一条新思路.
1 宏观经济风险评价指标体系的建立 1.1 宏观经济风险的定义宏观经济风险是指由于物价水平的波动和宏观经济活动而导致的企业利润损失的可能性[11],宏观经济风险是海外矿山项目并购顺利进行的重要影响因素之一.宏观经济周期性的波动、宏观经济变量的变动都会导致矿产品市场价格水平的变动,对矿产品价格和供求关系等经济变量产生较大的影响.所以,东道国的宏观经济状况是海外并购决策者投资决策的重要影响因素,宏观经济环境的优劣直接影响海外投资者的直接投资及股权投资.
1.2 指标体系的构建原则依据指标体系构建的基本原则,结合宏观经济评价的自身特点,在宏观经济评价指标设计时应遵循如下原则:
1) 科学性原则.宏观经济风险评价指标的设计必须符合相关统计学和经济学理论,各指标定义清晰.指标设计应简明扼要,不能过于简单造成信息的遗漏;也不能划分过于细化,造成指标相互重叠.
2) 系统性原则.宏观经济风险是把东道国或地区作为一个经济整体,考查其经济运行的总体状况.因此,要求指标选取应尽量全面、系统,最大限度地描述和反映出海外并购宏观经济风险的整体情况,以便对风险做出准确客观的评价[12].
3) 准确性原则.所谓准确性,主要包含两个方面,一是指标必须准确反映出东道国宏观经济的总体状态;二是指标数据必须是模型中所准确需要的,即满足模型对变量口径的要求.
4) 可比性原则.选取的指标必须符合统一的国际核算标准,对于不同的样本具有可比性,即能够在不同国家之间进行对比.例如,在选取反映国民经济总量的评价指标时,必须与国际通用的国民经济核算体系(SNA)中的相关指标的含义和统计口径相一致[13].
5) 可行性原则.要求所选指标便于分析、统计和易于获取,指标的选取应考虑指标数据获取的可行性和数据的可靠性,为海外并购够宏观经济风险评价的顺利进行奠定基础.
1.3 宏观经济主要风险因素的识别宏观经济政策的目标是保持经济增长、物价稳定、充分就业和国际收支平衡与汇率的稳定.基于此,在参考相关文献的基础上,从上述4个方面对宏观经济的主要风险影响因素进行识别.
1) 经济发展水平.经济发展水平是指一个国家或地区的经济发展规模、速度和达到的水准.东道国的经济发展水平和海外投资并购之间存在密切的联系,经济发展水平更高的国家可以吸收更多资本的流入,而外来资本又会促进东道国经济的发展.
2) 经济稳定性.经济稳定性是指保持经济持续、稳定、协调地发展,通常由平均经济增长率所体现.经济平均增长率越大,表示其经济越活跃,市场容量越大,经济稳定性越好,对矿产资源的投资开发就越有利.
3) 经济开放度.经济开放度是指允许别国资本渗透本国经济的程度和方式,东道国的经济开放程度越大,投资商的资本就越容易进入东道国市场,越有利于并购活动的顺利实施.
4) 物价水平.物价水平是度量东道国消费潜力的重要指标,也是一个国家财政状况和货币状况的风向标,通常由通货膨胀率所体现.持续较高的通货膨胀率会导致社会矛盾激化、社会不稳定因素增加、物价上涨甚至经济崩溃,对矿业企业海外并购的经济效益会造成严重影响.
5) 汇率风险.汇率风险是指由于汇率的波动而导致的风险,汇率波动会对海外投资盈亏、国际资本的流动产生较大的影响,增强或削弱投资方资本要素的比较优势.大幅度无预期的汇率波动会给投资方造成巨大的经济损失,海外并购活动一般以美元或东道国货币进行结算,汇率波动导致的货币价值变化对海外矿山项目并购的成败起到了关键性的作用[14].
6) 信用风险.信用风险又称违约风险,是指由于受信人不履行还本付息的义务,使授信人的实际收益与预期收益发生偏离的可能性[15].对于任何海外并购项目来说都会伴随着大量的债权债务关系,所以信用风险是必须考虑的又一重要风险因素,该类风险的评价是海外投资并购的重要保障.
7) 就业.就业是指在法定年龄内,有劳动能力和劳动愿望的人为获取收入或报酬而进行的有偿活动.就海外矿业投资并购项目而言,其偏向于劳动密集型产业,就业的波动和罢工活动可能会导致劳工风险,对海外矿山项目并购造成巨大的经济损失.
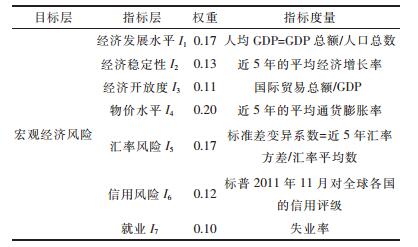
1.4 评价指标体系的建立基于对宏观经济风险因素的识别,建立了包括3个层次的评价指标体系,见表 1所示.
| 表1 海外矿山项目并购宏观经济风险评价指标体系 Table 1 Assessment index system of macroeconomic risk of oversea mine projects M & A |
 |
| 点击放大 |
1) 目标层.即海外矿山项目并购宏观经济风险.
2) 准则层.包含经济发展水平、经济稳定性、经济开放度、物价水平、汇率风险、信用风险和就业7个指标.
3) 因素层.即各个评价指标的量化方法.
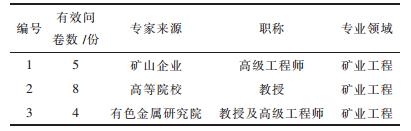
1.5 指标权重的确定采用德尔菲法,向矿山企业、高等院校、有色金属研究院的21名专家发出意见征询表,共计收回17份问卷,专家情况见表 2所示.经整理计算回收问卷,得到各风险指标权重见表 1.
| 表2 征询专家情况 Table 2 Consult professor situation |
 |
| 点击放大 |
2 海外矿山项目并购宏观经济风险评价模型的建立
通过将TOPSIS与灰色关联理论相结合,建立起海外矿山项目并购的宏观经济风险评价模型,既考虑了评价样本与理想解之间的相似程度,又考虑了样本内部因素的变化趋势与理想方案的区别,为海外矿山项目并购的有关风险评价提供新的途径[16-17].
2.1 构建加权标准化矩阵在对样本进行评价前,需要求得加权标准化矩阵Y.假设在海外矿山项目并购宏观经济风险评价中有m个待评价样本,n个风险评价指标,可以得到待评价的评价指标矩阵
1) 正、负理想解的确定依据正负理想解的定义,分别确定各个指标属性集的最大值和最小值,取负向型指标j-的最小值和正向型指标j+的最大值构成正理想解,取负向型指标j-的最大值和正向型指标j+的最小值构成负理想解[18].其数学表达式如下:
| $ Y_0^ + = \left( {\mathop {\mathop {\max }\limits_{1 \le i \le m} {y_{ij}}\left| {j \in {j^ + }} \right|,\mathop {\min }\limits_{1 \le i \le m} {y_{ij}}\left| {j \in {j^ - }} \right|}\limits_{} } \right) = \left( {y_1^ + ,y_2^ + y_3^ + \cdots y_m^ + } \right) $ | (1) |
| $ Y_0^ - = \left( {\mathop {\mathop {\min }\limits_{1 \le i \le m} {y_{ij}}\left| {j \in {j^ + }} \right|,\mathop {\max }\limits_{1 \le i \le m} {y_{ij}}\left| {j \in {j^ - }} \right|}\limits_{} } \right) = \left( {y_1^ - ,y_2^ - y_3^ - \cdots y_m^ - } \right) $ | (2) |
2) 样本到理想解的欧氏距离.设第i个样本至正负理想解的欧氏分别为Di+、Di-,则计算公式如下:
| $ D_i^ + = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_{ij}} - y_j^ + } \right)}^2}} } ,\left( {i = 1,2,3 \cdots m} \right) $ | (3) |
| $ D_i^ - = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_{ij}} - y_j^ - } \right)}^2}} } ,\left( {i = 1,2,3 \cdots m} \right) $ | (4) |
3) 样本到正理想解灰色关联度的计算依据计算出的加权标准化矩阵,计算第i个样本与第j个指标正理想解的灰色关联系数.
| $ s_{ij}^ + = \frac{{{{\min }_i}{{\min }_j}\left| {y_j^ + - y_{ij}^{}} \right| + \rho {{\max }_i}{{\max }_j}\left| {y_j^ + - {y_{ij}}} \right|}}{{\left| {y_j^ + - {y_{ij}}} \right| + \rho {{\max }_i}{{\max }_j}\left| {y_j^ + - {y_{ij}}} \right|}} $ | (5) |
式(5)中: ρ为分辨系数,一般取0.5.则该样本与正理想解的灰色关联系数矩阵可表示为:
| $ {W^ + } = \left[ {\begin{array}{*{20}{c}} {s_{11}^ + }& \cdots &{s_{1n}^ + }\\ \vdots &{\; \cdots }&{}\\ {s_{m11}^ + }& \cdots &{s_{mn}^ + } \end{array}} \right] $ |
样本i与正理想解的灰色关联度为:
| $ w_i^ + = \frac{1}{n}\sum\limits_{j = 1}^n {s_{ij}^ + } ,\left( {i = 1,2,3, \cdots m} \right) $ | (6) |
4) 样本到负理想解灰色关联度的确定同样以加权标准化矩阵为计算依据,计算样本i与正理想解第j个指标的灰色关联系数.
| $ s_{ij}^ - = \frac{{{{\min }_i}{{\min }_j}\left| {y_j^ - - y_{ij}^{}} \right| + \rho {{\max }_i}{{\max }_j}\left| {y_j^ - - {y_{ij}}} \right|}}{{\left| {y_j^ - - {y_{ij}}} \right| + \rho {{\max }_i}{{\max }_j}\left| {y_j^ - - {y_{ij}}} \right|}} $ | (7) |
样本与负理想解之间的灰色关联系数矩阵为:
| $ {W^ - } = \left[ {\begin{array}{*{20}{c}} {s_{11}^ - }& \cdots &{s_{1n}^ - }\\ \vdots & \cdots &{}\\ {s_{m1}^ - }&{\; \cdots }&{s_{mn}^ - } \end{array}} \right] $ |
样本i与正理想解的灰色关联度为:
| $ w_i^ - = \frac{1}{n}\sum\limits_{j = 1}^n {s_{ij}^ - } ,\left( {i = 1,2,3, \cdots m} \right) $ | (8) |
1) 欧氏距离和灰色关联度的无量纲化处理
| $ { \varphi_i} = \frac{{{ \phi_i}}}{{\mathop {\max \left( {{\phi _i}} \right)}\limits_{1 \le i \le m} }} $ | (9) |
式(9)中:
2) 综合无量纲化后的欧氏距离和灰色关联度di-和wi+的计算值越大,样本就与理想解越接近;di+和wi-的计算值越大,样本就与理想解越偏离.
| $ T_i^ + = \alpha d_i^ - + \beta w_i^ + $ | (10) |
| $ T_i^ - = \alpha d_i^ + + \beta w_i^ - $ | (11) |
式(10)、式(11)中: α和β反映的是决策者对形状拟合和位置距离的偏好程度,取值的大小取决于决策者的决策偏好,α和β满足
3)相对贴近度的计算相对贴近度
| $ {\delta _i} = \frac{{T_i^ + }}{{T_i^ + + T_i^\_}},\left( {i = 1,2,3 \cdots m} \right) $ | (12) |
4)样本相对贴近度排序依据
以我国某稀土公司拟进行海外稀土矿项目并购为例,进行案例分析
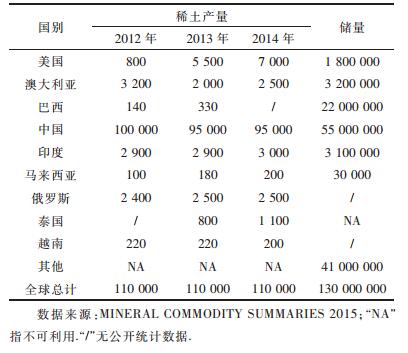
1) 确定评价对象依据全球稀土产量和储量的大小,选取前9位国家作为研究对象,评价其宏观经济风险的大小. 9个国家2012-2014年稀土产量以及储量情况如表 3所列.
| 表3 世界主要稀土国家产量和储量分布/t Table 3 Mine production and reserves of main rare earths countries /t |
 |
| 点击放大 |
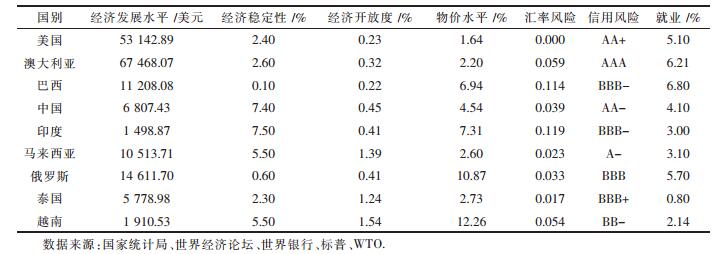
2) 原始数据的确定依据所建立的海外矿山项目并购宏观经济风险评价指标体系,确定各个国家各指标的实际值,结果见下表 4.
| 表4 9个国家的宏观经济情况 Table 4 Macroeconomic risk situation of nine countries |
 |
| 点击放大 |
3) 评价指标分级及分级值的确定
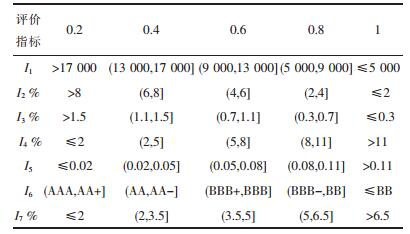
为了消除各指标值量纲的影响,便于对各个指标进行统一分析和最终风险值的计算,根据各指标实际值对各评价指标进行指标分级,分级规则见表 5.
| 表5 宏观经济风险评价指标分级规则 Table 5 Rate and scores of macroeconomic risk assessment index |
 |
| 点击放大 |
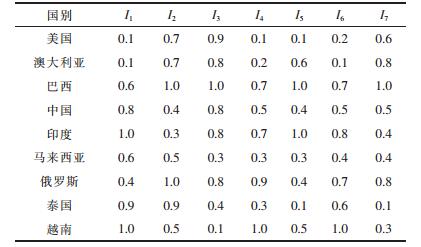
由各国各个风险指标的实际值,依据指标的分级规则(表 5),可确定各个国家各指标的分级值,见表 6.
| 表6 风险指标分级值 Table 6 Scores of risk assessment index |
 |
| 点击放大 |
4) 加权标准化矩阵将指标权重向量与指标分级值矩阵相乘,便得到加权标准化矩阵Y.
| $ Y = \left[ {\begin{array}{*{20}{c}} {0.017}&{0.091}&{0.099}&{0.020}&{0.017}&{0.024}&{0.060}\\ {0.017}&{0.091}&{0.088}&{0.040}&{0.102}&{0.012}&{0.080}\\ {0.102}&{0.130}&{0.110}&{0.140}&{0.170}&{0.084}&{0.100}\\ {0.136}&{0.052}&{0.088}&{0.100}&{0.068}&{0.060}&{0.050}\\ {0.170}&{0.039}&{0.088}&{0.140}&{0.170}&{0.096}&{0.040}\\ {0.102}&{0.065}&{0.033}&{0.060}&{0.051}&{0.048}&{0.040}\\ {0.068}&{0.130}&{0.088}&{0.180}&{0.068}&{0.084}&{0.080}\\ {0.153}&{0.117}&{0.044}&{0.060}&{0.017}&{0.072}&{0.010}\\ {0.170}&{0.065}&{0.011}&{0.200}&{0.085}&{0.120}&{0.030} \end{array}} \right] $ |
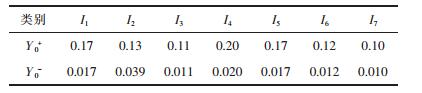
依据式(1)~式(2)确定每个指标的正负理想解,见表 7.
| 表7 各指标正负理想解 Table 7 Positive and negative ideal solution of each index |
 |
| 点击放大 |
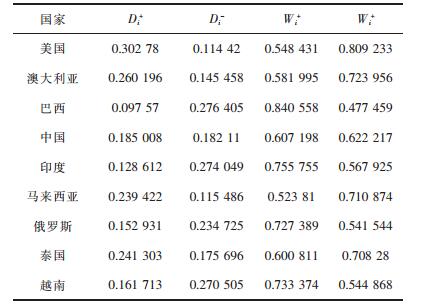
依据表 6确定的正负理想解,结合公式(3)~式(4)计算出样本至正、负理想解的欧式距离,再运用式(5)~式(8)计算出样本与正、负理想解的灰色关联度,计算结果见表 8.
| 表8 九个国家的欧氏距离和灰色关联度 Table 8 Euclidean distance and gray relation of nine countries |
 |
| 点击放大 |
3.3 计算相对贴近度
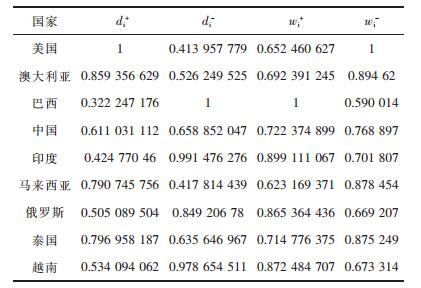
1) 欧式距离和灰色关联度的无量纲化处理依据式(9)对欧式距离和灰色关联度进行无量纲化处理,结果如表 9所示.
| 表9 无量纲化后的欧氏距离和灰色关联度 Table 9 Euclidean distance and gray relation after normalization |
 |
| 点击放大 |
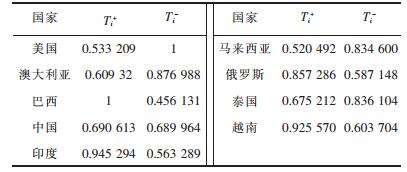
2) 综合无量纲化后的欧式距离和灰色关联度.根据式(10)~式(11)对欧式距离和灰色关联度进行综合,取α=β=0.5.计算结果见表 10.
| 表10 综合无量纲化后的欧式距离和灰色关联度 Table 10 Comprehensive result of euclidean distance and gray relation after normalization |
 |
| 点击放大 |
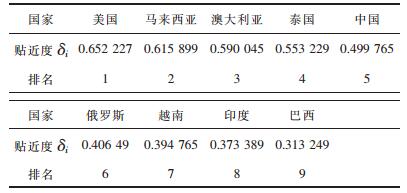
3) 相对贴近度的计算在一般评价中,越接近正理想解,样本就越好,但本文是对风险进行评价,故越接近负理想解的样本其风险值就越小,面临的风险就越低.故将式(12)转换为式(13)计算其相对贴近度,计算结果见表 11.
| $ {\delta _i} = \frac{{T_i^ - }}{{T_i^ + + T_i^\_}},\left( {i = 1,2,3 \cdots m} \right) $ | (13) |
| 表11 贴近度评价结果 Table 11 Assessment result of relative approach |
 |
| 点击放大 |
贴近度的计算结果见表 11.
贴近度计算结果表明:美国、马来西亚、澳大利亚三个国家的宏观经济风险处于“低”水平,这些国家物价稳定、投资吸引力高、经济发展水平较高,是海外矿山项目并购的首选国家;越南、印度、巴西这三个国家的宏观经济风险处于“高”水平.其中,越南的经济发展水平、物价水平、信用风险三项指标均较差,是宏观经济风险的极端指标;印度虽然经济增长相对较快,但其经济发展水平较差,汇率风险较高,且经济开放度不够高,使得其宏观经济风险大幅提高;巴西经济发展水平、汇率风险位于9个国家前列,但其就业、经济稳定性、经济开放度三个方面均为9个评价国家的最末,很大程度上提高了其宏观经济风险,在并购过程中应该注意这三项极端指标.因此,我国企业在进行海外矿业并购前,对东道国宏观经济风险的极端指标的防范至关重要.
4 结论1) 依据宏观经济政策的目标,结合矿产资源投资开发的自身特点,从经济增长、充分就业、物价稳定和国际收支平衡与汇率稳定四个方面进行了因素识别,建立了包含经济发展水平、经济稳定性、经济开放度、物价水平、汇率风险、信用风险以及就业七个指标的宏观经济风险评价指标体系.
2) 将TOPSIS和灰色关联度相结合,分别从位置距离和形状拟合性上反映备选方案与理想方案间的接近程度,构建了灰色理想点逼近的风险评价模型,并将模型运用于实证分析,以海外稀土矿资源并购为例,选取了全球稀土资源最为丰富的9个国家为研究对象,评价了这9国的宏观经济风险.
3) 9个稀土大国的宏观经济风险评价结果显示,美国、马来西亚、澳大利亚三个国家的宏观经济风险处于“低”水平,是我国企业海外稀土矿山项目并购的首选国家; 越南、印度、巴西三个国家的宏观经济风险较大,应尽量规避在这些国家投资.对于其余风险一般的三个国家,应当注意防范其极端风险指标的影响.
| [1] | 刘红霞.基于国家风险的我国企业跨国并购交易财务政策选择研究[J]. 中央财经大学学报,2014 (3):61–65. |
| [2] | 陈泽.中国企业海外并购风险形成因素的层次结构--基于ISM模型[J]. 中国地质大学学报,2013,13 (2):126–130. |
| [3] | 石予友.中国企业海外矿产资源并购风险评估及控制[J]. 中国流通经济,2012 (9):62–66. |
| [4] | 付沙.基于灰色模糊理论的信息系统安全风险评估研究[J]. 现代情报,2013,33 (7):34–39. |
| [5] | 马运来.基于TOPSIS法的区域风险投资环境综合评价[J]. 科技管理研究,2007 (7):160–164. |
| [6] | 张振辉.灰色系统理论在企业并购风险识别中的应用[J]. 科研管理,2003,24 (6):1–5. |
| [7] | 李晓莉.基于粗糙集的灰色TOPSIS法的第三方逆向物流供应商评价研究[J]. 科技管理研究,2013 (14):66–70. |
| [8] |
BEHZADIAN M, OTAGHSARA S K, YAZDANI M, et al. A state-of the-art survey of TOPSIS applications[J].
Expert Systems with Applications, 2012,39 (17):13051–13069. DOI: 10.1016/j.eswa.2012.05.056. |
| [9] | 张志峰.基于综合赋权C-TOPSIS法的航天器研制风险控制[J]. 东北大学学报,2015,36 (5):626–629. |
| [10] |
TORLAK G, SEVKLI M, SANAL M, et al. Analyzing business competition by using fuzzy TOPSIS method: An example of Turkish domestic airline industry[J].
Expert Systems with Applications, 2011,38 (4):3396–3406. DOI: 10.1016/j.eswa.2010.08.125. |
| [11] | 曹小琳.基于灰色关联分析与加权TOPSIS法的房地产私募基金风险评价研究[J]. 建筑经济,2014,35 (11):101–106. |
| [12] | 郑明贵, 陈艳红.世界稀土资源供需现状与中国产业政策研究[J]. 有色金属科学与工程,2013,3 (4):70–74. |
| [13] | 徐映梅.宏观经济运行质量评价指标的选择方法[J]. 中南财经政法大学学报,2007 (4):3–8. |
| [14] | 田长顺, 黄洪祥, 王志勇.金属非金属地下矿山通风系统评价指标体系[J]. 有色金属科学与工程,,4 (1):67–71. |
| [15] | 何问陶.我国宏观经济先行指标体系及对经济预测实证研究[J]. 南方金融,2007 (4):14–19. |
| [16] | 汪送.航空装备研制风险的综合赋权--双基点法评估[J]. 中国安全科学学报,2010,20 (11):124–129. |
| [17] | 李锋, 魏莹.一种改进的基于效用理论的TOPSIS决策方法[J]. 系统管理学报,2008,17 (1):82–87. |
| [18] |
LIN C, TSAI M. Location Choice for Direct Foreign Investment in New Hospitals in China by Using ANP and TOPSIS[J].
Qual Quant, 2010,44 (2):375–390. DOI: 10.1007/s11135-008-9199-2. |
| [19] | 陈孝新.灰色多属性群决策的TOPSIS法[J]. 江西财经大学学报,2008 (1):21–27. |
 2016, Vol. 7
2016, Vol. 7


