| 基于响应面优化法的某矿山充填配比优化 |
2. 江西理工大学资源与环境工程学院,江西 赣州 341000
2. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
随着国家对环境保护越来越重视,加上充填采矿法具有较低的贫化率和较高的回采率,能够充分的利用现有资源,并且能够控制地表的沉陷及控制地压等特点[1].充填采矿法得到越来越广泛的应用,充填体的强度受到灰砂比、养护天数、浓度等的影响[2-6].文献[6]对影响充填体强度影响因素进行了敏感性分析,但是没有考虑各个因素之间的交叉对充填体强度影响,比如灰砂比和养护天数、灰砂比和浓度、养护天数和浓度交叉对充填体强度的影响.响应面设计法能够得到各因素间的交叉作用影响,并且回归精度较高[7].在食品科学、机械工程、化学工程与技术、力学等领域应用较为广泛[8-11].矿山充填配比优化研究方法主要有实验法,即通过正交实验或者均匀设计实验来获得,也有建立神经网络预测模型预测矿山所需充填配比方案[12-15].目前利用响应面优化法进行充填体配比的研究还比较少,文献[16]应用响应面法研究影响粉煤灰胶结体抗压强度的主要因素及其影响程度,粉煤灰的含量是影响充填体单轴抗压强度的重要因素,文献[17]利用CCD响应面设计法对高寒矿山充填配比进行优化,其主要考虑的是温度、灰砂质量比、固相质量分数及其各因素的交叉的影响.本文基于BBD响应面设计法分析全尾砂胶结充填体强度的影响因素,及其最佳充填配比方案,主要考虑的影响因素为灰砂比、养护天数、浓度.
1 响应面设计法响应面设计(response surface method,RSM)通过中心组合实验,采用多元线性回归的方法,将实验中的各个因素及其交叉因素进行多项式拟合,再根据函数的响应面等值线和回归方程确定实验的最佳参数组合.最早的响应面函数没有考虑交叉项的一次表达式:
| $ y = g({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}}, \ldots {x_n}) = {a_{\rm{0}}} + \sum\limits_{i = 1}^n {{a_i}} {x_i} $ |
之后考虑了交叉项的表达式为:
| $ y = g({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}}, \ldots {x_n}) = {a_{\rm{0}}} + \sum\limits_{i = 1}^n {{a_i}} {x_i} + \sum\limits_{i = 1}^n {{a_i}} {x_i}{x_i} + \sum\limits_{i = 1}^n {{a_i}} {x_i}{x_j} $ |
其中xi为随机变量,a0、ai、aii、aij为待定系数,由样本点迭代确定.y为优化目标函数,其与真实值之间的误差为:
| $ \varepsilon = Y{\rm{-}}\alpha X $ |
其中Y为:
| $ Y = {\left[{{y^{\rm{1}}}\begin{array}{*{20}{c}} {}&{{y^{\rm{2}}}\begin{array}{*{20}{c}} \cdot & \cdot & \cdot &{{y^{n{\rm{-1}}}}}&{{y^n}} \end{array}} \end{array}} \right]^{\rm{T}}} $ |
为真实函数值向量,n为实验次数.
| $ \begin{matrix} X= \\ \left\lfloor \begin{align} & 1\ \ \ \ \ {{x}_{1}}\ \ \ \ \ {{x}_{2}}\ \ \ \cdots \ \ {{x}_{k}}\ \ \ \ x_{1}^{2}\ \ \ \ x_{2}^{2}\ \ \cdots x_{k}^{2}\ \ \ {{x}_{1}}\ \ \ {{x}_{2}}\ \ \ {{x}_{1}}\ \ {{x}_{3}}\ \ \cdots \ \ \ {{x}_{1}}\ \ \ {{x}_{3}}\ \ \cdots {{x}_{1}}\ \ {{x}_{k}}\ \ {{x}_{2}}\ \ {{x}_{3}}\ \ \cdots \ \ {{x}_{k-1}}\ \ {{x}_{k}} \\ & 1\ \ \ \ \ {{x}_{1}}\ \ \ \ \ {{x}_{2}}\ \ \ \cdots \ \ {{x}_{k}}\ \ \ \ x_{1}^{2}\ \ \ \ x_{2}^{2}\ \ \cdots x_{k}^{2}\ \ \ {{x}_{1}}\ \ \ {{x}_{2}}\ \ \ {{x}_{1}}\ \ {{x}_{3}}\ \ \cdots \ \ \ {{x}_{1}}\ \ \ {{x}_{3}}\ \ \cdots {{x}_{1}}\ \ {{x}_{k}}\ \ {{x}_{2}}\ \ {{x}_{3}}\ \ \cdots \ \ {{x}_{k-1}}\ \ {{x}_{k}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \\ & 1\ \ \ \ \ {{x}_{1}}\ \ \ \ \ {{x}_{2}}\ \ \ \cdots \ \ {{x}_{k}}\ \ \ \ x_{1}^{2}\ \ \ \ x_{2}^{2}\ \ \cdots x_{k}^{2}\ \ \ {{x}_{1}}\ \ \ {{x}_{2}}\ \ \ {{x}_{1}}\ \ {{x}_{3}}\ \ \cdots \ \ \ {{x}_{1}}\ \ \ {{x}_{3}}\ \ \cdots {{x}_{1}}\ \ {{x}_{k}}\ \ {{x}_{2}}\ \ {{x}_{3}}\ \ \cdots \ \ {{x}_{k-1}}\ \ {{x}_{k}} \\ & 1\ \ \ \ \ {{x}_{1}}\ \ \ \ \ {{x}_{2}}\ \ \ \cdots \ \ {{x}_{k}}\ \ \ \ x_{1}^{2}\ \ \ \ x_{2}^{2}\ \ \cdots x_{k}^{2}\ \ \ {{x}_{1}}\ \ \ {{x}_{2}}\ \ \ {{x}_{1}}\ \ {{x}_{3}}\ \ \cdots \ \ \ {{x}_{1}}\ \ \ {{x}_{3}}\ \ \cdots {{x}_{1}}\ \ {{x}_{k}}\ \ {{x}_{2}}\ \ {{x}_{3}}\ \ \cdots \ \ {{x}_{k-1}}\ \ {{x}_{k}} \\ \end{align} \right\rfloor \\ \end{matrix} $ |
| $ a=\left[ {{a}_{0}}{{a}_{1}}{{a}_{2}}\cdots {{a}_{k}}{{a}_{11}}{{a}_{22}}\cdots {{a}_{kk}}{{a}_{12}}{{a}_{13}}\cdots {{a}_{1k}}{{a}_{23}}\cdots {{a}_{k-1\cdot k}} \right] $ |
RSM主要包括Box-Behnken(BBD)、均匀外壳设计(Uniform Shell Design,USD)、中心组合设计(Central Composite Design,CCD)3种,本文采用BBD设计.
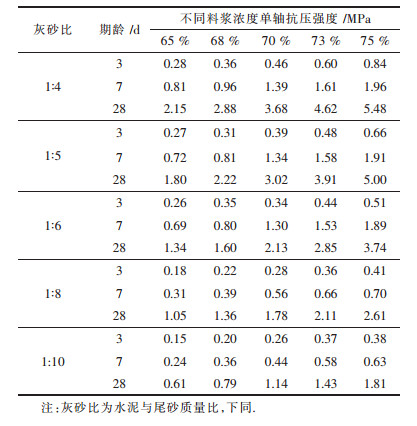
2 实验步骤首先确定单因素的取值范围,按照3因素3水平的BBD设计方法,确定各个因素的影响大小及最佳配比方案.本次数据来至某矿山的充填配比实验,如表 1所列.
| 表1 全尾砂胶结充填体单轴抗压强度 Table 1 The backfilling uniaxial compressive strength of cemented filling body |
 |
| 点击放大 |
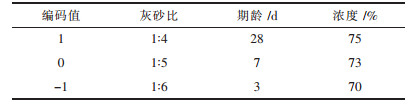
文献[6]指出,充填体的强度与灰砂比、养护时间、浓度的增加而增加.可以设定灰砂比为1:4、1:5、1:6,养护时间为3 d、7 d、28 d,浓度为70 %、73 %、75 %,其响应面分析因素水平表如表 2所列.
| 表2 响应面分析因素水平表 Table 2 Response surface analysis factors level table |
 |
| 点击放大 |
3 响应面优化试验
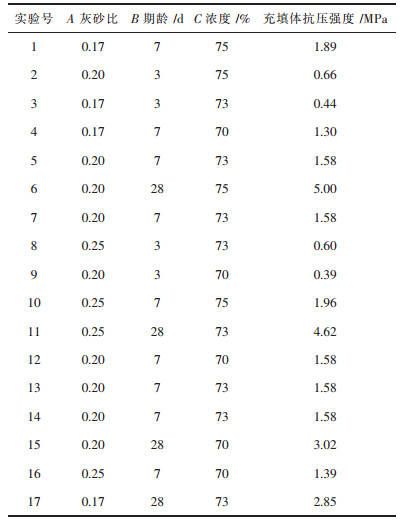
在单因素试验基础上,以灰砂比、期龄、浓度值为自变量,充填体单轴抗压强度为响应值,设计3因素3水平的响应面分析试验,试验的因素和水平、试验方案及结果见表 3.
| 表3 充填配比优化的响应面分析设计及结果 Table 3 Filling ratio optimization design of response surface analysis and the results |
 |
| 点击放大 |
3.1 回归方程的建立
对表 3的数据进行多元回归拟合,得到充填体强度(Y)对灰砂比(A)、期龄(B)、浓度(C)的二次多项回归模型为:
Y=3.17+0.4A+1.69B+0.56C+0.42AB+0.01AC+0.4BC-0.14A2-1.02B2+0.23C2
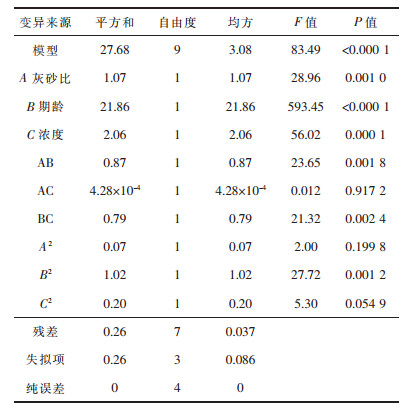
按照此模型对原数据进行预测,得到的预测值和实际值如图 1所示,该方程的相关系数为0.9908,校正决定系数0.9789,说明模型的相关性较好;变异系数为10.19%,表明实验的精确度较高;信噪比为7.64 > 4,说明方程能够很好的反应真实实验.方差分析表 4所示,该模型的P值小于0.0001,说明模型是显著的,不同的影响因子对充填体的强度影响显著,该方法能够准确可靠的模拟真实的3因素3水平.从表 4中可以看出充填体强度的影响因子中,期龄的影响大于浓度的影响,浓度的影响大于灰砂比的影响,这与原文献[6]的结论是一样的.交叉影响中,灰砂比与期龄的影响大于期龄和浓度对充填体强度的影响,灰砂比和浓度的交叉影响对充填体的强度不显著.A2、C2对充填体强度影响不显著,B2对充填体的强度较显著,说明表明试验因素对响应值的影响不是简单的线性关系,二次项对响应值也有很大的影响.根据多元回归拟合分析处理3个因素对充填体强度的响应面分析结果见图 2.
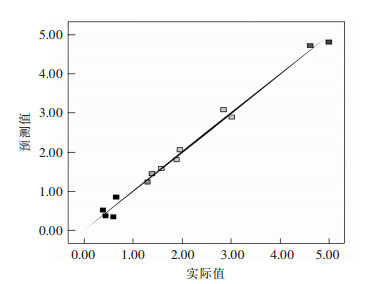 |
| 图 1 充填体预测值和实际值 Fig. 1 Predicted value and actual value of filling |
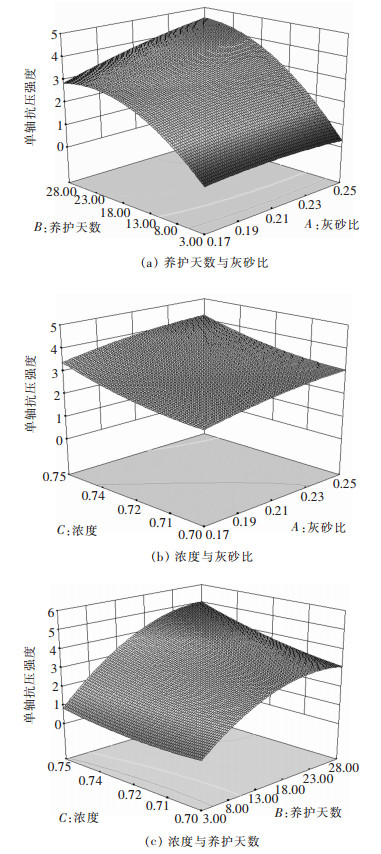 |
| 图 2 各两因素交互作用对充填体影响的响应面图 Fig. 2 The response surface figure about each two factors interaction on filling |
| 表4 响应面试验结果的方差分析结果 Table 4 Response surface test results of variance analysis |
 |
| 点击放大 |
3.2 模型的优化和验证
通过以上的分析,可以得到基于单轴抗压强度的最佳配比实验方案,灰砂比为1:4,养护天数为28 d,浓度为75 %,预测的最大单轴抗压强度为5.71 MPa, 按照此最佳参数进行实验得到的单轴抗压强度5.48 MPa,与理论值5.71 MPa的误差为4.2 %,真实值比理论值偏低,可能是试验过程中仍存在干扰因素,建议在后续深入研究过程中考虑的因素能更彻底、更全面.
4 结论通过响应面设计法对充填配比进行优化实验,可以发现响应面设计法不仅能够对单因素的敏感性进行分析,而且能够对考察各个因素的交叉对目标值的影响,并且分析其对目标值影响的大小排列.与传统实验相比,响应面优化实验能够在较少的实验次数下获得最优结果.充填体强度的影响因子中,期龄的影响大于浓度的影响,浓度的影响大于灰砂比的影响;交叉影响中,灰砂比与期龄的影响大于期龄和浓度对充填体强度的影响,灰砂比和浓度的交叉影响对充填体的强度不显著.A2、C2对充填体强度影响不显著,B2对充填体的强度较显著,说明试验因素对响应值的影响不是简单的线性关系,二次项对响应值也有很大的影响.真实值比理论值偏低,可能是试验过程中仍存在干扰因素,建议在后续深入研究过程中考虑的因素能更彻底、更全面.
| [1] | 张海波, 宋卫东, 许英霞.充填采矿技术应用发展及存在问题研究[J]. 黄金,2010 (1):23–25. |
| [2] | 余斌.影响尾砂胶结充填体强度的若干因素分析[J]. 河北冶金,2001 (3):3–6. |
| [3] | 罗建祥.影响胶结充填体强度的因素分析[J]. 甘肃冶金,2005,27 (2):24–25. |
| [4] | 邓代强, 高永涛, 姚中亮.胶结充填材料力学特性影响因素回归分析[J]. 有色金属工程,2008,60 (4):120–124. |
| [5] | 杨安国, 周宗红, 张秋华.胶结充填体抗压强度的影响因素分析[J]. 价值工程,2014 (23):80–81. |
| [6] | 付建新, 杜翠凤, 宋卫东.全尾砂胶结充填体的强度敏感性及破坏机制[J]. 北京科技大学学报,2014 (9):1149–1157. |
| [7] | 程敬丽, 郑敏, 楼建晴.常见的试验优化设计方法对比[J]. 实验室研究与探索,2012 (7):7–11. |
| [8] | 李梅青, 张瑜, 代蕾莉, 等.Plackett-Burman试验设计及响应面法优化超声辅助提取明绿豆SOD工艺[J]. 食品科学,2015 (2):69–74. |
| [9] | 石晶, 孙艳, 李卫民.某微型电动汽车前悬架系统性能分析与优化研究[J]. 机械设计与制造,2015 (3):65–68. |
| [10] | 王健, 刘晓玲, 宋永会, 等.微量金属元素投加量优化组合对污泥发酵产乙酸的影响[J]. 环境科学研究,2015,28 (1):149–156. |
| [11] | 张江, 彭程, 蔡琛芳, 等.基于响应面法的带喷流激波针参数优化研究[J]. 空气动力学学报,2015 (2):204–210. |
| [12] | 余海华, 宋卫东, 唐亚男, 等.阶段空场嗣后充填体法采场结构参数及充填配比优化[J]. 矿业研究与开发,2012,32 (6):10–14. |
| [13] | 张钦礼, 李谢平, 杨伟.基于BP神经网络的某矿山充填料浆配比优化[J]. 中南大学学报(自然科学版),2013,44 (7):2867–2874. |
| [14] | 崔学伟, 严荣富, 那米日.尾砂胶结充填配比优化研究[J]. 现代矿业,2014,539 (3):73–75. |
| [15] | 胡小勇, 刘浪, 李光辉, 等.基于均匀实验的矿山充填料浆配比优化研究[J]. 矿业研究与开发,2015,35 (3):7–12. |
| [16] | 王健, 吕宪俊, 胡术刚, 等.大掺量粉煤灰胶结充填料浆的胶结性能研究[J]. 中国矿业,2010,19 (3):95–98. |
| [17] | 赵国彦, 马举, 彭康, 等.基于响应面法的高寒矿山充填配比优化[J]. 北京科技大学学报,2013 (5):559–565. |
 2016, Vol. 7
2016, Vol. 7


