| 基于传热反问题的钢包热状态跟踪模拟 |
钢包是冶金工业的重要容器和钢铁制造流程的物流载体,在钢铁制造流程中担任着储存和转运钢水的关键作用[1-3].国内外学者对钢包传热做过大量研究[4-9], 但对于钢包边界条件的处理过于理想,认为钢包内壁温度为钢水温度或烘烤火焰的温度,即忽略了流体与包衬之间的接触热阻.同时在钢包传热的数值模拟中缺乏对计算温度场的误差判定与精度修正.而确定钢包温度场的传统方法是实测法,通过预埋热电偶在包衬内部或表面,或通过非接触式电子测温枪、红外成像仪等设备来检测包衬温度.但这些方法都受钢包内部温度较高、生产场地布局复杂、电子原件使用寿命较短、测量误差较大等限制而无法长时间现场使用.
通过传热反问题研究方法,对烘烤时的钢包温度场进行数学反演.反问题是一种比较成熟的广泛应用于冶金、材料、航空、石化等领域的反演方法[10-15],用比较容易求得的条件来计算不易得到的条件,具有实测法和软件模拟所不具备的优点.在文中先用Fluent软件模拟计算出火焰温度场以此得到较为精确的钢包内壁烘烤温度,然后建立钢包传热正问题数学模型,正向计算包衬温度场,与实测的包壳温度进行误差判定,然后采用正则化反演算法进行精度修正,再通过计算机语言实现整个计算过程的可视化,实现钢包烘烤温度场实时监控.
1 钢包传热正问题钢包传热正问题就是已知包壁的温度、热流密度或者换热系数三类边界条件来计算钢包的温度场,三类边界条件受生产条件、钢包材质、测量器材和测量方法等影响较大,得到的温度场分布需要加以修正,本文正问题主要计算钢包冷包烘烤过程的包衬温度场.
1.1 正问题计算模型进行正问题计算时,通常需要对钢包做如下简化:
1) 钢包看作一个圆桶状结构,钢包的高径比大,忽略圆周方向导热,仅考虑径向传热,将钢包传热看作一维的,简化后如图 1所示;
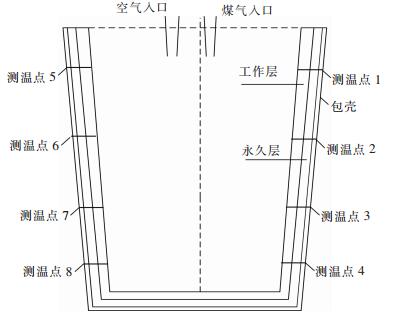 |
| 图 1 钢包模型 Fig. 1 Ladle model |
2) 烘烤时的火焰温度场较为固定,火焰在包壁处温度为烘烤温度,忽略包衬各层之间的接触热阻,外表面温度较高时存在对流与辐射2种换热形式;
3) 钢包沿口与空气的接触面积相对比较小,将其忽略作绝热处理;
4) 通过测温点1、2、3、4、5、6、7、8共8个点的实测温度推算钢包温度场,测温点1~4共4个点的位置离包口距离分别为1.4 m、2.4 m、3.1 m、4.2 m.
根据以上假设,包衬只存在径向传热,包壁的热传导控制方程为:
| $ \left\{ \begin{array}{l} \frac{{\partial T}}{{\partial \tau }} = \frac{1}{{\rho C}}\left[{\frac{1}{x}\frac{\partial }{{\partial x}}\left( {\lambda \cdot x\frac{{\partial T}}{{\partial x}}} \right)} \right]\\ - \lambda \frac{{\partial T}}{{\partial x}}{|_{x = 0}}=\left\{ \begin{array}{l} {Q_M} = {\rm{Const, }}T \in \left( {{\tau _{m - 1}}, {\tau _m}} \right)\\ {Q_t}, \tau > {\tau _m} \end{array} \right.\\ - \frac{{\partial T}}{{\partial x}}{|_{x = r}} = {Q_t}, \tau > {\tau _m}\\ T\left( {x, {\tau _{m - 1}}} \right) = {{\rm{T}}_{m - 1}}\left( x \right) \end{array} \right. $ |
其中ρ为密度-kg/m3;C为比热容,J/(kg·℃);λ为导热系数,W/(m·℃);T为温度, ℃;x为测点位置, m;τ为时间, s.
1.2 初始条件、钢包传热的边界条件 1.2.1 边界的对流换热通过Fluent计算软件对钢包烘烤时的火焰温度场分布进行模拟,得到钢包内气体的温度场如图 2所示,工作层内壁和包壳对流换热系数计算如下式:
| $ \begin{align} & N{{u}_{m}}=C\left( {{G}_{r}}\cdot {{P}_{r}} \right)_{m}^{n} \\ & {{G}_{r}}=g{{h}^{3}}{{\beta }_{m}}\Delta {T}/{V}\;_{m}^{2} \\ & \ \ \ \ \ \ {{\beta }_{m}}{{{1}/{T}\;}_{空气}} \\ & \ \ \ \ \ \ N{{u}_{m}}=\frac{\alpha h}{{{\lambda }_{m}}} \\ \end{align} $ |
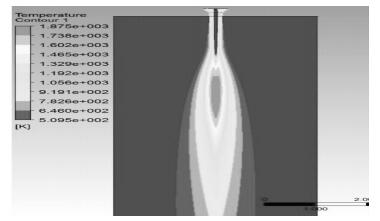 |
| 图 2 火焰温度场 Fig. 2 Temperature field of flame |
其中Num为包含了平均换热系数的平均谢努尔特准则,下角标m表示定性温度,对包衬内壁取边界层流体的温度,对包壳取为包壳温度;λ、Vm、Pr分别为空气的导热系数、运动粘度和普朗特数,α为对流换热系数,βm为空气的容积膨胀系数,h为轴向高度△x;根据换热面的形状和位置、换热边界条件以及流体处于层流或紊流的不同流态由传热手册查得,此处气流处于紊流取C=0.1,n=1/3.
1.2.2 边界的辐射换热包壳温度较低辐射换热可以忽略,包衬内壁辐射则需要充分考虑各个自由面之间的辐射热交换,同时内壁温度在轴向分布不同,还需将内壁分成n段,各段温度不一样,各段辐射强度不同,钢包辐射模型如图 3所示.
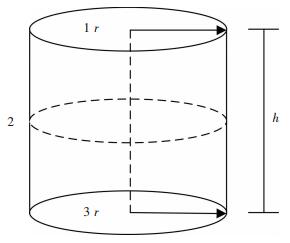 |
| 图 3 钢包辐射模型 Fig. 3 Ladle radiation model |
辐射强度公式:q=ε·σ·T气4,内壁总的辐射强度:
| $ {q_{内总}} = \sum\limits_{i = 1}^n {{q_i}} = \sum\limits_{i = 1}^n {\varepsilon \sigma \cdot T_i^4} $ |
内壁侧面自身之间的辐射角系数:
| $ {\varphi _{22}} = 1 + \frac{1}{2}\left[{\frac{h}{r}-\sqrt {{{\left( {\frac{h}{{2r}}} \right)}^2} + 1} } \right] $ |
包底对侧壁的辐射角系数:
| $ {\varphi _{32}} = \frac{1}{2}\left[{\frac{h}{r}-\sqrt {{{\left( {\frac{h}{{2r}}} \right)}^2} + 1} } \right] $ |
包盖对侧壁的辐射角系数:
| $ {\varphi _{12}} = \frac{1}{2}\left[{\frac{h}{r}-\sqrt {{{\left( {\frac{h}{{2r}}} \right)}^2} + 1} } \right] $ |
因此包衬内壁的综合辐射换热系数应该是侧壁、包底和包盖三部分的叠加,内壁划分后的某i段的综合辐射换热系数为:
| $ {q_{综合}} = \left( {{q_i} - {\varphi _{22}}\sum {{q_i}{S_i} - {q_{包底}}{S_{包底}}{\varphi _{32}} - {q_{包盖}}{S_{包盖}}{\varphi _{12}}} } \right)/{S_i} $ |
式中si为某点的小范围辐射面积,其高度为n/h.
1.3 正问题温度场数学计算一维传热采用有限差分法沿x方向将包衬按步长△x分割,得到节点i=0,1, 2,…,i,则工作层节点数学编号为P1~Pc,P1代表工作层内表面处;Pc代表工作层与永久层的交界面处;永久层节点数学编号为Pc~Pn,Pn代表永久层与包壳的交界面处;包壳节点数学编号为Pn~Ps,Ps代表包壳表面处;将时间从τ=0开始按步长△τ(时间迭代步长,即过一个△τ的时间计算一次包衬温度场)分割,得到k=0,1,2,…,坐标空间如图 4所示,内衬节点划分及测温点图 5所示.
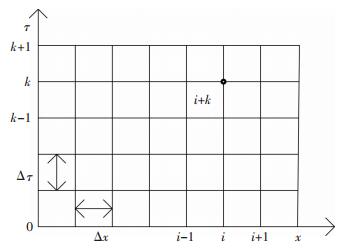 |
| 图 4 包衬导热网格图 Fig. 4 Thermal conducting grid of Ladle lining |
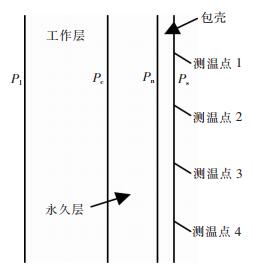 |
| 图 5 包衬节点划分及测温点 Fig. 5 Nodes dividing and temperature measuring points |
则空间任意点温度可表示为:
| $ T\left( {k\Delta \tau, i\Delta x} \right) = T\left( {\tau, x} \right) $ |
温度对时间的一阶导数用向前差商表示:
| $ \left( {\frac{{\partial T}}{{\partial \tau }}} \right)_i^k \approx \frac{{T_i^{k + 1} - T_i^k}}{{\Delta \tau }} $ |
温度对空间的二阶导数用中心差商表示:
| $ \left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}}} \right)_i^k \approx \frac{{T_{i + 1}^k - 2T_i^k + T_{i - 1}^k}}{{\Delta {x^2}}} $ |
内部节点温度差分方程为:
| $ T_i^{k + 1} = F\left( {T_{i + 1}^k + T_i^k} \right) + \left( {1 - 2F} \right)T_i^k $ |
对流边界节点差分方程为:
| $ T_m^{k + 1} = 2F\left( {T_{m + 1}^k + Bi \cdot T_f^k} \right) + \left( {1 - 2F - 2FBi} \right)T_m^k $ |
其中
通过上述公式按照时间和空间推进得到包衬随时间变化的温度场如图 6所示.
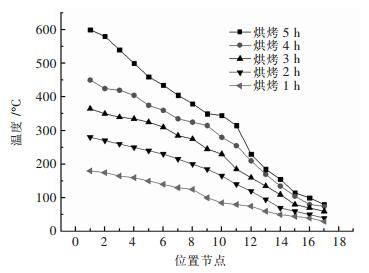 |
| 图 6 测温点3处包衬随时间的温度场 Fig. 6 Ladle lining temperature field of temperature measuring points 3 |
图 6是第3测温点处的包衬在分别烘烤1h、2h、3h、4h、5h后包衬在水平方向的温度分布,横坐标为包衬位置,0点处为工作层受热面,17点为包壳表面,从位置最低曲线到位置最高曲线大致反映了整个包衬的升温过程,也可以看出单独各个点的升温过程.
2 反问题温度修正正问题中通过已知或近似的边界条件对钢包温度场进行了计算,然而非稳态热传导是扩散型的,具有阻尼性和延迟性,阻尼性表现为边界热流的变化对边界附近的温度产生大的影响,而随着离边界距离的增加,热流变化的影响将减小,延迟性则表现为内部温度对边界热流的反应在时间上具有延迟性,某时刻的温度将影响接下来数个时刻的温度,但影响程度大小不同.因此,反演包衬温度场最有效的方法是按时间顺序估计而不是在全时间域一次估计,即顺序估计法是用接下来的TM,TM+1,TM+2…TM+R-1共R个时刻的包壳实测温度来估计τM-1时刻的温度TM-1.从τ=0时刻开始,已知包衬初始温度场T0,以T0为已知条件计算τ1、τ2…τM+R-1时刻的温度场T1、T2、T3…TM+R-1,得到包壳以及包衬内部测温点各时刻的计算温度T(τ1, Ps),T(τ2, Ps)…T(τM+R-1, Ps),然后与实测的包壳温度T实(τ1, Ps),T实(τ2, Ps) … T实(τM+R-1, Ps)和内部测温点的实测温度进行对比(钢包在径向共计N个测温点),并进行精度判定,若计算温度与实测温度之间相差较大,则需要进行温度修正.在钢包周转过程中的较短时间内可假设[16].
1) 钢包周转的短时间内包衬各层内部的热流密度呈线性分布;
2) 钢包周转的短时间内某点的热流密度呈线性变化.
根据以上两条假设可以得出包衬某点短时间内热流密度变化幅度是一样,当时间间隔相同时可令
| $ \phi = \sum\limits_{i = 1, j = 1}^{i = R, j = N} {{{\left( {{T_{实}}\left( {{\tau _i}, {x_j}} \right) - {T_{计算}}\left( {{\tau _i}, {x_j}} \right)} \right)}^2}} $ |
工作层内壁节点P1在τM-1时刻热流密度为:
| $ {Q_{{P_1}}} = Q\left( {M - 1, {P_1}} \right) = {\lambda _1}\frac{{{T_{计算}}\left( {M - 1, {P_1}} \right) - {T_{计算}}\left( {M - 1, {P_1} + 1} \right)}}{{\Delta x}} $ |
工作层和永久层交点处节点Pc在τM-1时刻热流密度为:
| $ {Q_{{P_c}}} = Q\left( {M - 1, {P_{\rm{c}}}} \right) = {\lambda _1}\frac{{{T_{实测}}\left( {M - 1, {P_{\rm{c}}}} \right) - {T_{实测}}\left( {M - 1, {P_{\rm{c}}} + 1} \right)}}{{\Delta x}} $ |
永久层和包壳交界处节点Pn在τM-1时刻热流密度为:
| $ {Q_{{P_{\rm{n}}}}} = Q\left( {M - 1, {P_{\rm{n}}}} \right) = {\lambda _1}\frac{{{T_{实测}}\left( {M - 1, {P_{\rm{n}}}} \right) - {T_{计算}}\left( {M - 1, {P_{\rm{n}}} + 1} \right)}}{{\Delta x}} $ |
包壳节点PS在τM-1时刻热流密度为:
| $ {Q_{{{\rm{P}}_{\rm{s}}}}} = Q\left( {M - 1, {P_{\rm{s}}}} \right) = {\lambda _3}\frac{{{T_{实测}}\left( {M - 1, {P_{\rm{s}}}} \right) - {T_{计算}}\left( {M - 1, {P_{\rm{s}}} + 1} \right)}}{{\Delta x}} $ |
工作层节点P1~Pc之间热流密度线性变化率、永久层节点Pc~Pn之间热流密度线性变化率、包壳节点Pn~Ps之间热流密度线性变化率依次为:
| $ \begin{array}{l} \Delta {Q_{\rm{n}}} = \frac{{{Q_{{{\rm{P}}_1}}} - {Q_{{{\rm{P}}_{\rm{c}}}}}}}{{{x_{{\rm{Pc}}}} - {x_{{\rm{P}}1}}}}\left( {{P_1} \le n \le {P_{\rm{c}}}} \right)\\ \Delta {Q_{\rm{n}}} = \frac{{{Q_{{\rm{Pc}}}} - {Q_{{\rm{Pn}}}}}}{{{x_{{\rm{Pn}}}} - {x_{{\rm{Pc}}}}}}\left( {{P_{\rm{c}}} \le n \le {P_{\rm{n}}}} \right)\\ \Delta {Q_{\rm{n}}} = \frac{{{Q_{{\rm{Pn}}}} - {Q_{{\rm{Pn}}}}}}{{{x_{{\rm{Pn}}}} - {x_{{\rm{Ps}}}}}}\left( {{P_{\rm{c}}} \le n \le {P_{\rm{s}}}} \right) \end{array} $ |
对于任意一个如图 7所示的长宽高分别为△x、y、z的单元网格,单位时间内流入的热流密度为Q进,流出的热流密度为Q出.
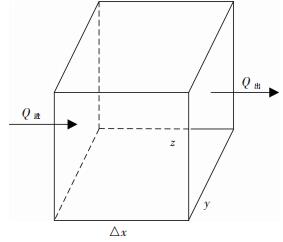 |
| 图 7 单元网格热流图 Fig. 7 Heat flow chart of unit grid |
单位时间单元网格温度变化量△T为:
| $ \Delta T = \frac{{\left( {{Q_{{\rm{进}}}} - {Q_{{\rm{出}}}}} \right)yz}}{{\rho cyz\Delta x}} = \frac{{\Delta {Q_{\rm{n}}}}}{{\rho c\Delta x}} $ |
包衬从工作层、永久层、包壳的比热容依次为c1、c2、c3,密度为ρ1、ρ2、ρ3,TM-1的修正可以用枚举法进行搜索,所有节点的T计算(M-1)每次修正量为△T,△T为某网格节点单位时间的温差,由于一个△τ内温度变化不明显,故m次迭代计算后进行一次反问题温度修正,所以有:
工作层节点P1~Pc修正后的温度、永久层节点Pc~Pn修正后的温度、包壳节点Pn~Ps修正后的温度依次为:
| $ \begin{array}{l} T = {T_{{\rm{计算}}}}\left( {M - 1, n} \right) - \frac{{\Delta {Q_{\rm{n}}}}}{{{\rho _1}{c_1}\Delta x}}\\ T = {T_{{\rm{计算}}}}\left( {M - 1, n} \right) - \frac{{\Delta {Q_{\rm{n}}}}}{{{\rho _2}{c_2}\Delta x}}\\ T = {T_{{\rm{计算}}}}\left( {M - 1, n} \right) - \frac{{\Delta {Q_{\rm{n}}}}}{{{\rho _3}{c_3}\Delta x}} \end{array} $ |
或者:工作层内部节点P1~Pc修正后的温度、永久层内部节点Pc~Pn修正后的温度、包壳内部节点Pn~Ps修正后的温度依次为:
| $ \begin{array}{l} T = {T_{{\rm{计算}}}}\left( {M - 1, n} \right) - \frac{{\Delta {Q_{\rm{n}}}}}{{{\rho _1}{c_1}\Delta x}}\\ T = {T_{{\rm{计算}}}}\left( {M - 1, n} \right) - \frac{{\Delta {Q_{\rm{n}}}}}{{{\rho _2}{c_2}\Delta x}}\\ T = {T_{{\rm{计算}}}}\left( {M - 1, n} \right) - \frac{{\Delta {Q_{\rm{n}}}}}{{{\rho _3}{c_3}\Delta x}} \end{array} $ |
温度修正范围:T计算-m·△T·△τ≤T≤T计算+m·△T·△τ,m是使T计算(M-1,n)与T计算(M+m,n)之间有较大温差的迭代次数,即
m·△T·△τ≥T计算(M-1+m,n)-T计算(M-1,n)=σ
σ指T计算(M-1,n)在m次迭代后的变化量,单位为℃.当得到修正后的温度场TM-1,计算新的τM时刻的温度场TM,再求φ,在修正范围内φ取得最小值的情况作为TM-1的准确值.不难看出此处默认接下来各时刻的温度受前一时刻的温度影响程度是一样的,但实际却是时间越接近τM影响程度越大,所以计算中R不宜过大.特殊的当R=1,N=1时情况最简单,以包壳实测温度为对照进行修正.当采用计算机c#语言进行计算后,包壳上的1、2、3、4、5、6、7、8点可设置红外测温电子枪,所得温度数据直接输入计算机,具体计算流程如图 8所示.
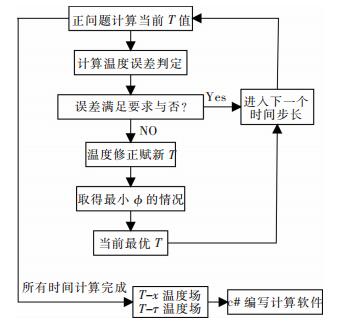 |
| 图 8 计算流程图 Fig. 8 Calculating process |
3 模拟实验及结果 3.1 现场数据采集
采用某钢厂210 t钢包为计算实例,钢包高5.2 m,内腔深度4.06 m,包口外径4.63 m,包口内径3.96 m,1、2、3、4测温点距离包口距离分别为1.4 m、2.4 m、3.1 m、4.2 m,所需数据如表 1,计算所需物性数据来源于北京科技大学与Q钢厂合作的“钢包信息管理系统”,通过现场取样委托测试公司试验测得.
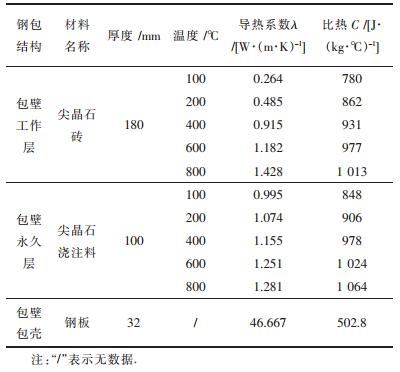
| 表1 包衬的物性参数 Table 1 Physical parameters of ladle lining |
 |
| 点击放大 |
根据“钢包信息管理系统”中吴鹏飞做的工作[17]可以知道工作层温度基本上是处于800℃以下,永久层基本上是处于600℃以下,包壳基本上处于300℃以下,包壳的导热系数和比热基本不变,根据导热系数与温度、热容与温度的对应关系拟合出导热系数-温度关系式、热容-温度关系式.但是为了减少计算量,加快计算速度,导热系数和热容在温度变化量为50℃时变化较小,因而工作层温度在0℃~50℃时λ取中间值0.185,c取中间值750,工作层温度在775℃~8250℃时λ取中间值0.185,c取中间值750,其余温度区间选取相应的拟合函数值.以此类推,热容也采用同样的方法选取.用有限差分法将1、2、3、4测温点处的包衬在水平方向划分为17个节点,内壁为1点,包壳为17点,时间间隔根据显示差分的波动性要求取△τ=9.2 s,以前一时刻的温度为基础,计算接下来各△τ时刻的包衬温度场并判定精度,判定精度值m取为0.03,TM-1以上下波动幅度6 ℃为界作为修订范围.计算以R=2,N=1为例,一个△τ内包衬温度变化很小,烘烤时间较长,为了得到可以加以修正的可观的累积计算误差,进行精度判定时每15个△τ即2.3 min进行一次温度修正,根据现场烘烤制度和喷嘴形状以及流体速度等因素确定火焰温度场,进而求得所需要的边界条件.
3.2 编写计算程序采用C#编程语言,以.net为开发平台,将烘烤过程实现计算机程序化,得到如图 9所示包衬温度场曲线图.
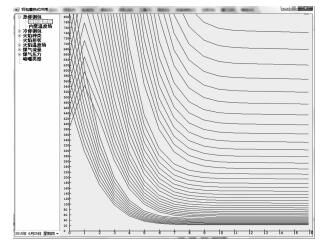 |
| 图 9 包衬温度场曲线图 Fig. 9 Ladle lining temperature field curve |
3.3 计算结果
具体计算中时间长,节点多,下面是部分抽取的计算结果:
图 10是1、2、3、4测温点从16:40开始的20 h内的实测温度,可以看出包壳温度各处随时间的升温速率是不一样的,当烘烤18 h后各自的温度上升变慢,趋近于一个固定值.
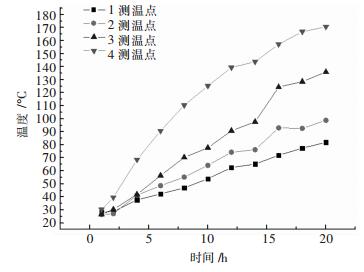 |
| 图 10 包壳实测温度 Fig. 10 Measured temperature of ladle lining outside surface |
图 11是测温点2从23:30开始1 h内的实测温度、计算温度、修正温度的对照图,可以看出修正后的温度误差明显减小,当计算温度误差较小时系统不修正.
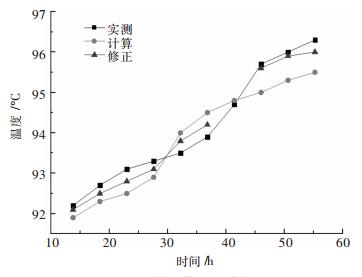 |
| 图 11 修正温度场 Fig. 11 Modified temperature field |
图 12是烘烤5 h后各测温点处包衬在水平方向的温度场,可以看出内部包衬蓄热明显,传递到包壳的热量较少,包壳温度较低.
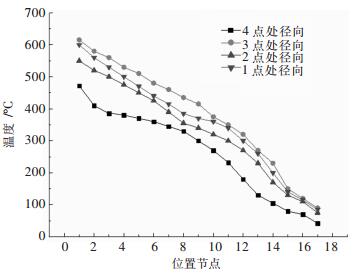 |
| 图 12 烘烤5h后的温度场 Fig. 12 Temperature field after preheating 5 h |
4 结论
本文为钢包烘烤时的包衬温度场在线追踪与预测提供了一种新方法,整个工作分为正文题求解、反问题的求解和温度场精度修正.先建立钢包的传热数学模型,根据钢包数据和烘烤制度,采用有限差分求解正文题,顺序函数法求解反问题并进行精度修正,包壳外面一定距离布置测温电子枪,然后计算得到的温度与实测进行精度对比,以某钢厂210 t钢包为例编程可以得到修正的包衬温度场随时间的变化图,为炼钢厂的钢包调度和编制合理的烘烤制度提供了一个切实可行的新方法.
| [1] | 刘占增, 郭鸿志.钢包传热研究的发展与现状[J]. 钢铁研究,2007,35 (1):59–62. |
| [2] | 季乐乐, 贺东风, 徐安军, 等.蓄热式钢包烘烤的数值模拟[J]. 钢铁,2013,48 (4):76–81. |
| [3] | 吴鹏飞, 徐安军, 贺东风, 等.绝热层对钢包热行为的影响[J]. 北京科技大学学报,2012,5 :0–14. |
| [4] | 潘学峰, 周海斌, 朱苗勇.连铸中间包内钢液温度变化规律的研究[J]. 中国冶金,2007,17 (10):45–49. |
| [5] |
FREDMAN T P, TORRKULLA, SAXEN H. Two-dimensional dynamic simulation of the thermal state of ladles[J].
Metallurgical and Materials Transactions B, 1999,30 (2):323–330. DOI: 10.1007/s11663-999-0061-2. |
| [6] |
GLASER B, GÖRNERUP M, SICHEN D. Thermal modelling of the ladle preheating process[J].
steel research international, 2011,82 (12):1425–1434. DOI: 10.1002/srin.v82.12. |
| [7] | 褚福强, 吴晓敏, 朱毅, 等.氧化铝纤维传热方式及反问题研究[J]. 工程热物理学报,2015,8 :029. |
| [8] | 王旭东, 臧欣阳, 杜凤鸣, 等.基于实测温度的结晶器瞬态传热反问题计算方法[J]. 铸造技术,2014,7 :34–39. |
| [9] | 梅宁, 焦思.基于工程反问题的圆管湍流流体热物性参数反演[J]. 中国海洋大学学报:自然科学版,2014,44 (10). |
| [10] | 高强权, 王堃, 陈林海.利用共轭梯度法反演钢包内钢液温度分布[J]. 世界科技研究与发展,2013,35 (005):578–581. |
| [11] | 唐光星.基于传热反问题方法的连铸凝固传热数学建模研究[D].大连理工大学, 2010:45-60. http://cdmd.cnki.com.cn/article/cdmd-10141-2010111120.htm |
| [12] |
BOZZOLI F, CATTANI L, RAINIERI S, et al. Estimation of local heat transfer coefficient in coiled tubes under inverse heat conduction problem approach[J].
Experimental Thermal and Fluid Science, 2014,59 :246–251. DOI: 10.1016/j.expthermflusci.2013.11.024. |
| [13] |
JIN T, HONG J, ZHENG H, et al. Measurement of boiling heat transfer coefficient in liquid nitrogen bath by inverse heat conduction method[J].
Journal of Zhejiang University SCIENCE A, 2009,10 (5):691–696. DOI: 10.1631/jzus.A0820540. |
| [14] |
LÖHLE S, FUCHS U, DIGEL P, et al. Analysing inverse heat conduction problems by the analysis of the system impulse response[J].
Inverse Problems in Science and Engineering, 2014,22 (2):297–308. DOI: 10.1080/17415977.2013.780170. |
| [15] |
MOVAHEDIAN B, BOROOMAND B. The solution of direct and inverse transient heat conduction problems with layered materials using exponential basis functions[J].
International Journal of Thermal Sciences, 2014,77 :186–198. DOI: 10.1016/j.ijthermalsci.2013.10.021. |
| [16] | BECK J V, Blackwell B, Clair Jrcrs. Inverse heat conduction Ill-posed problems[M]. James Beck, 1985:88-94. |
| [17] | 吴鹏飞.大型预制块钢包热行为过程数值模拟与优化研究[D].北京科技大学, 2012:46-54. |
 2016, Vol. 72
2016, Vol. 72


