| 钨骨架/Zr基非晶合金材料的静态力学行为 |
块状非晶合金原子排列具有短程有序、长程无序的特征,发生塑性变形时结构上没有类似金属材料的晶界、位错等缺陷。这些特点决定了块状非晶合金具有比晶态合金更加优异的力学性能,如高强度、高硬度、高韧性等[1]。然而在室温环境单轴压缩或拉伸条件下,块状非晶合金极易形成高度集中局部剪切带并迅速扩展,导致材料出现宏观脆性断裂而无明显塑性变形,该行为限制了其工程上的应用。块状非晶合金表面、界面具有很强的抑制结晶形核能力,同时其熔点相对较低,非常适合与其他材料复合制备出性能更加优异的复合材料[2]。金属钨具有极高的熔点和良好的导热性,使得金属钨成为非晶复合材料增强相的首选材料。关于增强相的存在形式主要有集束钨丝、钨骨架2种[3]。集束钨丝/Zr基非晶合金复合材料压缩强度高达2500 MPa,同时具有很高的塑性,其断裂模式由基体非晶合金单一的局部剪切带断裂演变为剪切断裂与钨丝劈裂、屈曲等混合模式,致使其成为优越的穿甲材料之一[4]。关于钨丝体积分数、钨丝直径、钨丝排列方式对复合材料力学性能与断裂模式的影响,国内外已展开了相关系统研究。钨骨架/Zr基非晶合金复合材料[5-6]也叫网络交叉复合材料,是由非晶合金基体材料与钨骨架增强相相互交叉形成的3维连通网络结构,基体与增强相之间相互渗透的结构使其最大程度发挥每种成分对复合材料的强化作用。目前关于钨骨架/Zr基非晶合金复合材料的研究并不多[7-8],主要是因为钨颗粒的体积分数、颗粒尺寸大小、随机分布方式等因素影响复合材料的力学性能与断裂模式,系统研究起来工作量大,也相当困难。
采用渗流铸造法制备出钨骨架/ZrTiCuNiBe复合材料,在室温环境下对其静态力学性能进行研究,结合电镜扫描(SEM)结果,探讨其变形断裂机理,为该复合材料的进一步应用研究提供相关依据。
1 实验选用ZrTiCuNiBe五元合金为基体材料,母合金以纯度大于99.5%或更高纯金属配制。为使母合金成分均匀,采用钨极电弧熔炼,合金反复熔炼4次以上;为避免其表面杂质干扰,采用超声波在酒精中清洗。采用电弧炉将基体材料与预制的钨骨架在真空的石英管中加热至略高于熔点温度处(等温15分钟,保证完全熔化)熔化母合金,使基体的金属液充分渗透到预制的钨骨架材料中;再在饱和的NaCl盐水中快速冷却,制备的复合材料中钨颗粒体积分数为40%。为了获得准确的静态压缩实验结果,避免实验结果受到摩擦、惯性、2维效应的影响,采用线切割将复合材料制备成Ф8 mm×5 mm压缩试样。室温下准静态压缩采用CSS-44300型电子万能试验机进行,应变率分别为10-3s-1、10-2s-1;为保证实验数据的可靠性,每个应变率下进行3次实验。将回收后的压缩试样表面加水细磨、抛光后,加入腐蚀液侵泡,在适当的温度下干燥后,用SU9000型扫描电子显微镜(SEM)对复合材料的原始组织和断口形貌、裂纹扩展等情况进行观察研究。
2 实验结果与分析 2.1 原始复合材料微观组织结构图 1为原始复合材料的微观组织结构图,图 1a为纯的钨骨架颗粒微观形貌图,黑色代表钨颗粒,白色为粘结剂[9]。图 1b中可以观测到钨骨架均匀地嵌套在黑色非晶基体相中,钨骨架与非晶相之间接触完好,未发现明显的孔洞与杂质,说明材料的制备工艺是可行的。
 |
| 图 1 原始复合材料的微观组织结构图 Fig. 1 the original microstructure of composite materials |
2.2 室温下复合材料准静态压缩
在静态压缩实验中,数据采集系统得到的是该压缩试样实时载荷与位移关系,试样的工程应力-应变关系如下[10]:
| $ {\sigma _e} = \frac{{4F}}{{{\rm{\pi }}d_0^2}}\;\;\;\;{\varepsilon _e} = \frac{{{l_0} - l}}{{{l_0}}}\;\;\;\;\;{{\dot \varepsilon }_e} = \frac{{{\rm{d}}{\varepsilon _e}}}{{{\rm{d}}t}} $ | (1) |
式(1)中,F为压缩载荷, d0、l0分别为压缩试样原始直径和长度,${\sigma _e}$、${\varepsilon _e}$、${{\dot \varepsilon }_e}$、分别为工程应力、工程应变、工程应变率,l为试样压缩过程中瞬时长度。
试样在压缩过程中,认为体积保持不变,得到
| $ Al = {A_0}{l_0} $ | (2) |
式(2)中,A0为试样初始面积, A为试样压缩过程中瞬时面积。
结合(1)、(2)式,试样的真实应力、应变为
| $ \left\{ \begin{array}{l} {\sigma _t} = \frac{F}{A} = \frac{F}{{{A_0}}}\left( {1 - {\varepsilon _e}} \right)\\ {\varepsilon _t} = \ln \frac{l}{{{l_0}}} = \ln \frac{l}{{1 - {\varepsilon _e}}} \end{array} \right. $ | (3) |
图 2为复合材料在室温下应变率分别为10-3 s-1、10-2 s-1的应力-应变曲线。曲线起始阶段出现一小段直线和微小的拐点,原因是实验中实验机与试样垫块有一段小间隙和实验机圆球压头找正,不影响实验结果判读。图 2中可以看出复合材料的应力-应变曲线经历非线性弹性阶段和应变强化阶段,表现出良好的弹塑性,屈服强度和压缩强度很大。对比基体材料的应力-应变曲线(如图 3),屈服后出现应变软化现象,之后断裂,塑性很小。当应变率由10-3 s-1提高到10-2 s-1时,复合材料屈服强度由1317 MPa上升到1451 MPa,增大了约10.2%;相应地,弹性模量由8.8 GPa上升到9.8 GPa,增大了约11.4%;塑性应变超过了0.2,抗压强度高达2000 MPa以上。而基体材料屈服强度由1210 MPa上升到1214 MPa,基本保持不变,塑性应变为0.08-0.12,之后试样很快断裂。图 4中12代表93钨[9]的静态拉伸应力-应变曲线,材料屈服强度约1400MPa,塑性应变约0.08。根据复合材料的复合准则[11]可以预测随着钨颗粒体积分数的增加,复合材料的强度将会增加。图 2-3可以看出,复合材料强度略大于基体材料,塑性显著增加,这正是其中加入钨骨架的结果。
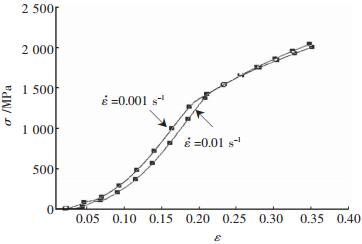 |
| 图 2 复合材料室温下准静态应力-应变曲线 Fig. 2 the stress-strain curve of composites at room temperature under quasi-static |
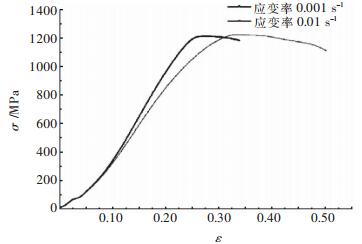 |
| 图 3 基体材料室温下准静态应力-应变曲线 Fig. 3 the stress-strain curve of matrix material at room temperature under quasi-static |
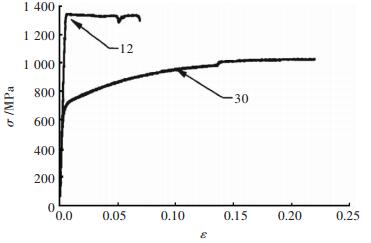 |
| 图 4 93钨室温下的静态应力-应变曲线 Fig. 4 the stress-strain curve of 93W at room temperature under quasi-static |
2.3 复合材料准静态断裂特性
图 5为复合材料应变率分别是10-3 s-1、10-2 s-1时静态压缩后回收试样的宏观形貌图。图 5中可以看出裂纹最初产生于试样边缘,然后逐步向中心扩展的;同时可以发现应变率由10-3 s-1提高到10-2 s-1时,裂纹数量、开裂程度变大,宏观上没有观察到明显的剥落坑。
 |
| 图 5 复合材料静态压缩宏观形貌图 Fig. 5 the macro morphology of quasi-static compression composite |
图 6、图 7为复合材料应变率分别为10-3s-1、10-2s-1时静态压缩后回收的试样断裂SEM图。从图 7(b)、图 7(c)中可以看到,复合材料中钨骨架的断裂主要是沿着钨颗粒与非晶基体结合界面的沿晶断裂和钨颗粒的穿晶断裂。同时发现沿晶断裂部分,钨颗粒基本保持原有形态,颗粒表面光滑无缺损;然而穿晶断裂中有明显的解理台阶,说明钨颗粒的断裂为脆性穿晶解理断裂。镶嵌在钨骨架之间的非晶基体则基本保持了原有形态的完整性,倾向于出现沿晶断裂,在断面上留下凹坑。该行为说明复合材料的断裂不再是非晶合金的纯剪切断裂,这和武晓峰等[12]研究结果一致。图 6(c)、图 7(b)、图 7(c)中有明显微裂纹出现,裂纹的传播扩展并非是直线式的,主要沿着钨颗粒与非晶基体结合界面或者在钨颗粒中传播。传播过程中绕过非晶基体出现许多弯曲转向、分叉等现象,最终裂纹终止在非晶基体上。造成复合材料中裂纹特殊扩展方式的原因是,材料制备后在冷却过程中,由于基体与钨骨架的热膨胀上面的差异,制备的复合材料中必定存在热应力;在热应力作用下,钨骨架处于压应力状态,而基体处于拉应力状态;复合材料在变形时,基体中的残余拉应力使裂纹向钨骨架颗粒扩展,钨骨架能够有效的抑制裂纹的扩展或使裂纹前端转向。裂纹的传播特点说明复合材料中非晶基体对于裂纹的传播起一定的约束阻碍作用。裂纹起源于钨骨架,非晶基体对裂纹传播有若干程度的桥联效果,吸收部分裂纹扩展所需的能量,降低裂纹前端应力强度因子,从而提高复合材料的强度。同时在图 6(b)、图 7(b)中局部区域发现少许的脉状花样和非晶的热软化熔融现象,这是局部温升过高造成的。图 8(a)、图 8(b)为93W应变率为2×10-3 s-1静态拉伸微观形貌图,可以发现钨颗粒的断裂为解理断裂,钨颗粒间存在微裂纹。
 |
| 图 6 复合材料应变率为10-3 s-1静态压缩微观形貌图 Fig. 6 the composite quasi-static compression micro topography at strain rate of 10-3s-1 |
 |
| 图 7 复合材料应变率为10-2 s-1静态压缩微观形貌图 Fig. 7 the composite quasi-static compression micro topography at strain rate of 10-2s-1 |
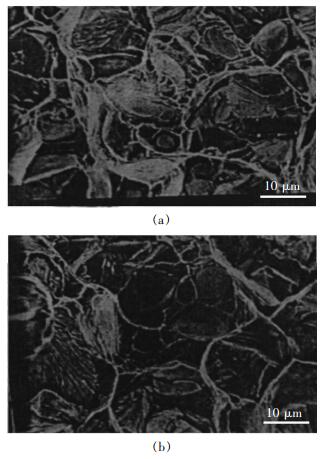 |
| 图 8 93W应变率为2×10-3 s-1静态拉伸微观形貌图 Fig. 8 the 93W quasi-static tensile micro topography at strain rate of 2×10-3 s-1 |
3 讨论 3.1 裂纹起源的形成
非晶基体材料中,其变形在高度集中局域化的剪切带内进行[12]。剪切带的形成目前认为是在剪切应力作用下,非晶合金粘滞性滑动产生塑性变形造成的。然而在复合材料中未发现大量剪切带,说明复合材料中钨颗粒的尺寸大小随机性、形状不规则性等特点造成其断裂模式完全不同于基体材料。从图 6、图 7中发现复合材料的裂纹起源于钨骨架中。我们认为复合材料为非均质材料,在部分较大钨骨架颗粒的压缩变形初期中,由于基体与钨颗粒在结构上是嵌套的,使其不能以常规的剪切断裂方式失效。钨颗粒与基体的结合界面强度很高,不会导致结合界面成为裂纹起源的诱发点,SEM图中能同时观测到钨骨架的两种断裂方式证明了这一点。其次,钨颗粒本身具有一定的塑性,在颗粒周围的基体上很容易造成应力集中现象[13],当压缩载荷继续施加,应力集中加剧,达到一定程度时使钨颗粒萌生微裂纹,成为整个变形中的起始点。如图 1所示,在复合材料中钨颗粒所占密度比例较大的部分,在非晶基体中很难形成剪切带,压缩载荷主要集中在钨颗粒上,颗粒首先变形形成微裂纹,颗粒对剪切带的形成起阻碍作用。
3.2 复合材料与基体材料的应力-应变曲线对比图 2、图 3中最明显的区别在于:复合材料塑性、压缩强度均大于基体材料塑性和断裂强度,复合材料出现应变硬化效应,基体材料出现应变软化效应。复合材料整个变形过程及图 5所示的宏观形貌图可以看出,复合材料在垂直于受力方向上被横向压缩伸长,外围钨颗粒部分最先出现裂纹,中心部位仍处于非线性弹性变形阶段,随着外围裂纹向中心部位传播、扩展,复合材料因横向伸长产生的拉应力增大,该行为可以解释其应变硬化效应。不同应变率(10-3s-1、10-2s-1)下的静态应力-应变曲线、静态压缩微观形貌的差异应该归咎于基体材料内部特征-自由体积的变化。剪切带的诱发形成、传播扩展与变形局部区域自由体积的凝结程度密切相关,两种实验状态下微观形貌差异是由应变率效应带来的,而其根本原因是应变率对自由体积的影响。变形过程中自由体积的浓度大小是由不断加载的剪切应力造成自由体积的凝聚、结构弛豫造成自由体积湮灭相互竞争结果控制的。
3.3 脉状花样形成原因分析目前关于非晶合金的断裂机制目前还处于研究阶段,大部分研究人员认为是非晶合金中塑性流变造成的。关于非晶合金塑性流变主要有2种理论[14-17]:一是自由体积理论,它认为非晶的塑性流变起源于应力驱动单原子的跳跃导致自由体积的产生;二是剪切转变区理论,它则认为塑性流变是原子团簇做剪切运动造成原子集团的不可逆重排造成的。这两种理论的结果都会造成剪切带粘度的降低,粘度的降低使非晶合金发生软化直至断裂。剪切带粘度降低时最典型的微观特征通常表现为脉状花样的形式,越来越多的工作表明脉状花样的产生是剪切带内绝热温升和自由体积共同作用产生[18]。图 6(b)、7(b)中局部区域发现小面积的脉状花样和少许的非晶熔融现象,说明非晶基体在断裂过程中没有发生大面积的流变现象;也就是说钨骨架的交叉结构可以避免非晶合金断裂过程中发生大面积的流变,从而提高复合材料强度。
钨骨架和非晶基体的嵌套交叉结构使得复合材料在压缩变形时,其断裂模式发生变化。对于非晶基体材料而言,由于受到钨骨架颗粒的穿插,只能在其剪切变形区小面积范围内产生很小的剪切面,大面积的流变的形成条件无法满足。从另一方面来讲,复合材料的高塑性致使静态压缩时间较长,压缩过程中其变形区域内产生的热量很快消散掉。温度没有达到非晶基体玻璃转变温度或者非晶基体的熔点,因此无法形成大面积流变。小面积流变的发生可能是部分小区域范围内剧烈变形、局部温度过高造成的。
4 结论采用渗流铸造法制备出直径为8 mm、钨颗粒体积分数达40%的非晶基复合材料,通过对复合材料与基体材料进行静态压缩实验。同时结合93W的静态拉伸应力应变曲线,对比3种材料的应力-应变曲线,对回收试样做电镜扫描,得出如下结论:
1)复合材料的塑性和强度均高于基体材料,且复合材料出现应变硬化现象,基体材料出现应变软化现象。
2)复合材料断裂模式为一种混合断裂模式,有沿着钨颗粒与非晶基体结合界面的沿晶断裂、钨颗粒的脆性穿晶解理断裂,复合材料性能的提高完全由钨骨架颗粒起主导作用。
3)复合材料未发生大面积流变,小面积范围内发现脉状花样。主要原因是复合材料内嵌套交叉结构使得基体在其局部产生很小的剪切面,大面积流变的形成条件无法满足。
| [1] |
WANG W H. The nature and properties of amorphous matter[J].
Progress in Physics, 2013,33 (5):176–352. |
| [2] |
MORGANA M T, NARESH N T. Mechanical properties of bulk metallic glasses[J].
Progress in Materials Science, 2010,55 :759–839. DOI: 10.1016/j.pmatsci.2010.04.002. |
| [3] |
CONNER R D, DANDLIKER R B, JOHNSON W L. Mechanical properties of tungsten and steel fiber reinforced Zr41.2Ti13.8Ni10Cu12.5Be22. metallic glasses matrix composites[J].
Acta Mater, 1998,46 (17):6089–6102. DOI: 10.1016/S1359-6454(98)00275-4. |
| [4] | 陈小伟, 李继承, 张方举, 等.钨纤维增强金属玻璃复合材料弹穿甲钢靶的实验研究[J]. 爆炸与冲击,2012,32 (4):346–354. |
| [5] | 周伟, 胡文彬, 张荻.挤压铸造制备三维连续网络结构增强金属基复合材料[J]. 上海交通大学学报,1999,33 (7):779–782. |
| [6] |
WEGNER L D, GIBSON L J. The mechanical behavior of interpenetrating phase composites-I:Modelling[J].
International Journal of Mechanical Sciences, 2004,42 (5):925–942. |
| [7] |
XUE Y F, WANG L, CHENG H W, et al. Dynamic tensile property of Zr-based metallic glass/porous W phase composite[J].
J.Mater.Sci.Technol, 2010,26 (10):908–913. DOI: 10.1016/S1005-0302(10)60146-6. |
| [8] |
WEI X S, VEKSHIN B, KRAPOSHIN V, et al. Full density consolidation of pure aluminium powders by cold hydro-mechanical pressing[J].
Materials Science and Engineering A, 2011,528 :5784–5789. DOI: 10.1016/j.msea.2011.03.099. |
| [9] | 刘筱玲.钨合金材料性能测试及宏细观力学分析[D].成都:西南交通大学, 2001. http://cdmd.cnki.com.cn/article/cdmd-10613-2004106171.htm |
| [10] | 卓家寿, 黄丹. 工程材料的本构演绎[M]. 北京: 科学出版社 , 2009 . |
| [11] | 张国定, 赵昌正. 金属基复合材料[M]. 上海: 上海交通大学出版社 , 1996 . |
| [12] | 刘娜, 才鸿年, 王鲁, 等.Zr基非晶合金准静态压缩下的多重剪切带行为[J]. 北京理工大学学报,2006,26 (10):916–920. |
| [13] | 武晓峰, 张海峰, 丘克强, 等.原位合成ZrC颗粒增强错基非晶复合材料及力学性能[J]. 金属学报,2003,39 (5):555–560. |
| [14] |
FA LK, M L., LANGER, J S.. Dynamics of viscoplastic deformation in amorphous solids[J].
Physical review E, 1998,57 :7192–7205. DOI: 10.1103/PhysRevE.57.7192. |
| [15] |
WANG W H, DONG C, SHEK C H. Bulk metallic glasses[J].
Materials Science and Engineering R, 2004,44 (s2-3):45–89. |
| [16] |
WANG W H. The elastic properties, elastic models and elastic perspectives of metallic glasses[J].
Progress in Materials Science, 2012,57 :487–656. DOI: 10.1016/j.pmatsci.2011.07.001. |
| [17] |
JIANG M Q, WILDE G, DAI L.H. Origin of stress overshoot in amorphous solids[J].
Mechanics of Materials, 2015,81 :72–83. DOI: 10.1016/j.mechmat.2014.10.002. |
| [18] |
XIE S, GEORGE E P. Size-dependent plasticity and fracture of a metallic glass in compression[J].
Intermetallics, 2008,16 :485–489. DOI: 10.1016/j.intermet.2007.11.013. |
 2016, Vol. 7
2016, Vol. 7


