| 第一性原理计算在相图计算中的应用研究进展 |
2. 国家离子型稀土资源高效开发利用工程技术研究中心,江西 赣州 341000
2. National Engineering Research Center for Ionic Rare Earth, Ganzhou 341000, China
相图是体系处于热平衡条件下的几何描述,是研究凝固、相变、晶体生长、固态相变的基础,能够为材料设计提供重要的结构和性能方面的指导[1].根据相图所提供信息,可以对材料进行主动设计,从而脱离了过去被动应用材料的阶段,我国无机非金属材料专家郭景坤院士曾预言,材料设计将成为未来六大发展领域之一[2].
20 世纪70 年代以来,相图与热化学的计算机耦合即相图计算CALPHAD (Calculation of Phase Diagram)[3]技术迅速崛起,成为研究相图的一种新趋势[4-8].CALPHAD 技术避免了传统实验测定所带来的工作量大、耗时长、所得数据不准确等问题,利用热力学和相图的自洽一致性检验相图,由此一大批的二元、三元以至更多元相图的准确性得到了大幅度的提高.然而,CALPHAD 技术也存在以下弱点: 依赖于实验获得的数据进行计算; 无法计算平衡条件下亚稳相、金属间化合物的结构和合金的稳定性;且由于传统数据库中热力学数据匮乏,使得优化相图范围有限,对于很多新发现的体系或化合物,往往找不到相关热力学数据用于CALPHAD 计算.
随着第一性原理计算方法的出现,CALPHAD 研究进入了一个崭新的阶段,许多热力学性质如结合能、形成热和相变热等均可由第一性原理计算得到.其原理是仅通过m0,e,h,c,kB 5 个基本物理常数,采用密度泛函得到体系的总能量和电子结构,进而机算出结合能、生成能、相变热等热力学参量,为CALPHAD计算平衡相图提供支持.近年来,利用第一性原理计算相图已取得了许多不错的成绩.
本文综述了CALPHAD 技术及目前存在的问题,第一性原理研究相图的优势,以及第一性原理在 CALPHAD 当中的应用研究进展,并结合相关实例,对运用第一性原理计算相图的几个方面进行了阐述.
1 CALPHAD 技术利用实验构筑相图的主要方法有差热分析法、化学分析法、金相显微分析法及X 射线衍射分析法等.然而,由于样品纯度达不到实验所需要求,体系内部存在着低温下扩散速度慢,高温液相线难测的阻力,以及低熔点及易挥发金属高温不稳定等各项限制性因素的制约,导致实验测定难以得到真正的相平衡信息.加之,实验测定的人为干扰因素较大,同一个实验,不同的人做出的结果相差甚大,如Sc-Al 体系的 ScAl2化合物[9].并且,通过实验测定得到一个完整相图的工作量仍然是相当惊人的,即使只是一个普通的二元系相图,也需要耗费相当长时间的工作量,更何况三元乃至四元系的相图的研究.
20 世纪70 年代以来,从热力学理论出发计算相图成为了相图研究的新趋势,即CALPHAD 技术.CALPHAD 技术经历了Kaufman[10]和Hillert[11]等的继承和发展,已逐步形成介于相平衡、热化学和溶液理论三者之间的一个成熟分支.由CALPHAD 方法计算得到的相图,具有高度的自洽一致性,在很大程度上减少了实验所需工作量,已成为相图研究的热门领域和材料设计的重要工具.
由CALPHAD 方法计算相图,前提是通过文献调研的方法获取体系所需的相平衡及热力学数据,在此基础上,选择合适的热力学模型对体系各相吉布斯自由能进行合理描述,如对液相,可以采用正规溶液模型、亚正规溶液模型、似化学模型、缔合溶液模型、离子双亚晶格模型等来描述,之后权衡各实验数据,确定优化权重,直至得到的优化参数在误差范围内和实验结果吻合良好.随后可从优化得到的各项参数中提取相关的热力学信息,如各相区组成、相比例、活度及混合焓等.
由此可见,CALPHAD 技术的基础是合理筛选出体系所需实验数据,进而进行一系列热力学计算,最终得到各相平衡信息.随着传统材料体系的研究深入和新材料体系的不断被发现,相关的相图和热力学实验数据十分匮乏,CALPHAD 技术的应用及发展随之遇到了瓶颈.传统CALPHAD 技术也无法计算亚稳相、金属间化合物的结构和合金的稳定性,导致运用CALPHAD 进行计算时精确度不高,甚至出现错误,无法满足日益增长的材料设计要求.
2 第一性原理第一性原理,又称为“第一性原理计算”(Firstprinciples Calculations),即从量子力学出发,从电子层面上计算凝聚态和孤立个体中原子和电子的行为.原子之间的成键方式可由量子力学描述并给出合理的量化解释,而成键方式可直接决定材料的内部结构,从而影响材料的各方面性能.因此,从理论上来说,任何材料的性能都可以通过第一性原理进行合理预测,而无需任何经验参数的选取,仅通过求解薛定谔方程来得到.但这种描述只是一种理想化状态,实际上,多体物质中原子与电子之间存在着强烈的相互作用,会造成求解薛定谔方程时出现一定程度的偏差,对此,需引入近似或假设的方法来修正计算结果,使其在误差范围内精确可信[12].
由于原子核的质量与电子质量之比为3 个数量级,从动量守恒理论可以推断,原子核与电子的速度相差甚大,因此,出现了以“原子核静止”理论为基础的波恩-奥本海默近似(Bom-Oppenheimer approximation),也称为“绝热近似”[13],它的原理是把原子和电子的运动分开考虑,即考虑原子核的运动时视电子为静止,同理,考虑电子的运动时视原子核为静止,这样一来,只通过求解电子的薛定谔方程即可.然而,电子之间的相互作用并没有通过波恩-奥本海默近似的引入而真正消失,直到Hartree-Fock[14]近似的出现,它在波恩-奥本海默近似的基础上,提出了“电子等式场”假设,即只考虑一个电子的作用,把周围的其他电子近似处理成分布均匀的等势场,从而把多体问题转换成了单体问题,也称之为平均场近似.Hartree- Fock[14]近似求解的单体系薛定谔方程为非线性,需进行多次自迭代求解,且没有考虑相对效应及电子关联能,即电子间自旋反平衡时存在的排斥作用,因而在精确求解键能反应过渡态问题时仍然存在很大的漏洞,但为之后被广泛应用的密度泛函理论(density function theory,即DFT)[15-16]奠定了理论基础.密度泛函理论这一概念最初源于Thomas-Fermi[17]模型,它在 Hartree-Fock 近似的基础上取得了一定的进步,但是并没有能够很好的解决上述问题.密度泛函理论的发展,由最初的Thomas-Fermi 模型的建立,到Hohenberg- Kohn[18]定理的提出,直至最后Kohn-Sham[19]方程的成型,其理论部分逐步趋于完善,Kohn-Sham 方程从形式上把多电子系统基态特性问题转化为有效的单电子问题,其解释比Hartree-Fock 近似更加严谨,也更加简单易懂,且由此引入了交换失联能这一概念,而交换失联能又可细分为局域密度近似[20-22]和广义梯度近似[23-25],后者在前者的基础上有很大的改进,在计算过渡金属和分子晶体体系时也更加精确.
Xavier Gonze 等提出了密度泛函微扰理论[26],将局域密度近似用于密度泛函理论,有效预测针对小的原子位移或无穷均匀电场等不同扰动的周期系统响应.利用这种技术,获得了由于绝热扰动的总能量变化,在实验数据的百分之几之内.Gonze X 等进一步开发了线性和非线性响应函数计算程序,包含于 ABINIT 开源计算软件包中[27-28].用含时密度泛函微扰理论(TDDFT—对分子)或多体微扰理论(GW 近似)近似计算激发态.固体中许多与电声相互作用有关的性质如红外、拉曼和中子衍射谱等都可由晶格点阵动力学得到,基于密度泛函微扰理论的线性响应技术,使得对点阵动力学的从头计算成为了可能.经 ABINIT 得到的声子色散已能直接与中子衍射实验相比,后续经计算得到的声子谱,可以进一步得到体系的许多物理性质.
除ABINIT 软件外,第一性原理的计算软件还有 MS[29]、VASP 软件[30]、SIESTA[31]、WieN2k[32]、ATAT[33]等,其中应用较为广泛的是VASP 软件[30].VASP 采用平面波基组,利用投影缀加波(Projector-augmented wave,PAW)[34]或者超软赝势[35]描述核和电子的相互作用.PAW 方法或超软赝势的应用使得计算所需的平面波基组数大大减小,同时,由于采用了高效的矩阵对角化算法[36-37]和Pulay/Broyden 电荷密度混合方法[36, 38-40],计算效率和收敛情况一般好于其他采用平面波基组的软件包.ATAT 计算程序包则能够与VASP 等几种国际主流计算程序结合使用.ATAT 是合金理论研究工具的集合体,有MIT Ab -initio Phase Stability(MAPS)、Easy Monte Carlo Code (EMC2) 、Constituent Strain Extension(CSE)和gensqs 几个主要子代码.在无序合金中的应用较为广泛,准简谐模型、可转移力常数、晶格动力学第一性原理研究、热力学性质、电子激发态计算、部分化合物的预测、多元合金相中寻找新强化相、尤其在相图计算方面有着很大的应用优势.
3 第一性原理在CALPHAD 中的研究进展将第一性原理计算应用于相图可以避开一些实验数据不足所带来的困扰,从量子力学的观点出发,通过求解一系列非经验参数,最终得到体系所需的热力学信息,如化合物的形成焓、混合焓、相变热、结合能等,而且,第一性原理计算是唯一可以得到亚稳相信息的工具,这对于CALPHAD 及实验方法而言都是不可能实现的,另外,第一性原理计算还可以为 CALPHAD 提供建模所需如相的短程有序、晶体结构及缺陷等信息.因此,第一性原理的计算与CALPHAD的结合,为材料设计和性能的提升开辟一条新途径,已成为相图计算研究的热点之一.第一性原理计算应用于CALPHAD 技术进行相图计算的流程图如图 1 所示.
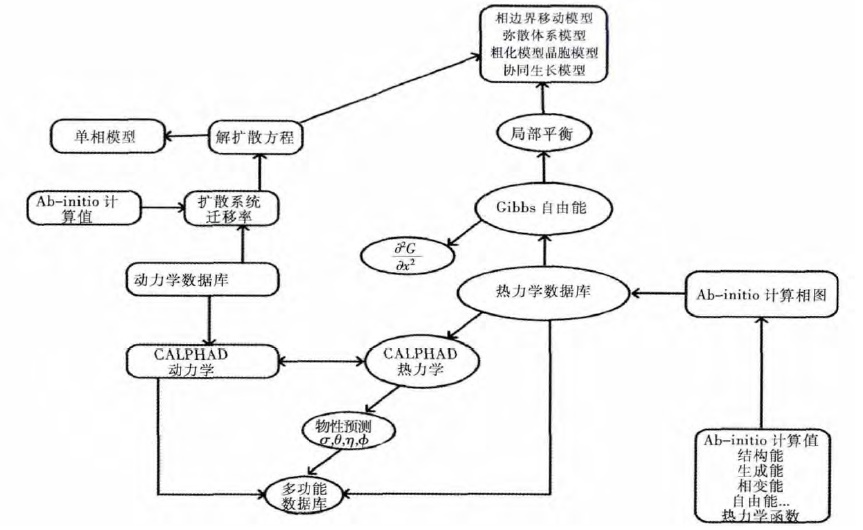 |
| 图 1 第一性原理计算在CALPHAD 技术中的应用流程 Fig. 1 Application of first principle calculation in CALPHAD |
2001 年,Kaufman F 等[41]利用第一性原理与CALPHAD相结合计算了Ta-W 相图,CALPHAD 计算时用到的如生成焓、相变反应热等相关热力学信息均由第一性原理计算得到.随后Colilet C[42]运用类似的研究方法,以表格的形式总结了多个二元合金体系和部分三元合金体系的相图.陈星秋等[43]基于第一性原理的密度泛函理论,计算了MMn2(M:Sr、Y、Lu、Ti、Zr、Hf、 Nb)多个体系较低温度下的相变热,同时计算了Ti- A1 系中3 个中间相化合物TiAl3,TiAl,Ti3Al 的生成热,与有关实验数据相比,计算结果在误差范围内吻合良好.
近年来,有关第一性原理计算在CALPHAD 技术中的应用研究方兴未艾.在合理预测化合物的能量性质、相图、动力学性质等方面,均取得了实质性的进展.以下将从上述3 个方面对第一性原理计算在 CALPHAD 中的应用研究进行阐述.
3.1 化合物的能量性质化合物的能量性质包括结构能、生成热、相变热、热力学性质等方面,对化合物能量性质的研究,有利于开发其潜在的应用价值.目前,运用第一性原理计算得到化合物的电子结构及晶格参数,可以很好的预测还未被发现化合物的结合能等一系列能量性质,将预测得到的结果与CALPHAD 相结合,来进行新型材料的研究,已成为近年来材料领域研究的热点.稀土(RE)、钨(W)、铜(Cu) 是我国的特色资源,相关体系的研究相对集中,以下针对近年来第一性原理在以上3 个方面的能量性质计算进行简要概述见表 1.
| 表1 各合金系化合物能量性质计算结果 Table 1 Calculation results of energy properties of alloy systems |
 |
| 点击放大 |
3.1.1 RE(稀土)系合金
赵燕燕[44]基于第一性原理下的CASTEP 模块,研究了M(Ag,Cu,Ni)-Ce 合金的晶格常数、生成焓、结合能及弹性常数,研究结果表明:Ag-Ce 体系中,AgCe、Ag2Ce、Ag4Ce 的形成焓及结合能均为负值,其中Ag4Ce 在热力学的理论上最易形成,且其稳定性也最好; 另外,对Cu-Ce 体系中间相CuCe、Cu2Ce、 Cu3Ce、Cu4Ce、Cu5Ce、Cu6Ce 及Ni -Ce 体系中间相 Ni2Ce、Ni3Ce、Ni7Ce2、Ni5Ce、Ni3Ce7也分别进行了类似的研究;赵沙斐[45]通过对AI4RE 和AI2REZn2(RE= La,Ce)合金的研究,发现AI2LaZn2的形成焓及热稳定性都低于AI4La,同理,AI4Ce 及AI2CeZn2的性质比较;曾梦雪[46]对Mg12RE(RE=Ce,Pr,Nd) 的弹性性能以及电子结构利用第一性原理进行了计算,计算所得的形成焓表明,Mg12RE 合金的稳定性随RE 的原子序数的增加而降低.另外,通过对电子结构及电态密度分布的研究,证实了tI26 型Mg12RE 合金中RERE和RE-Mg 间共价键的存在.镁稀土合金处具有镁元素带来的高强度、低密度等优点外,还兼备了通过掺杂少量稀土而达到的强化明显增强的效果.在第一性原理的帮助下,苏昕[47] 重点研究了Mg-RE(RE=Y,La,Sm)的电子结构及固溶体力学行为,并在此基础上,对Mg-6Sm-0.4Zn-0.3Zr 合金在225 ℃温度下的结晶过程进行了描绘;Chen G 等[48]采用VASP软件包对Mg-Zn-Re-Zr 合金中的2 种二元合金相 Mg2Y 和Mg2La 的电子结构、弹性及热力学性质进行了计算,其中Mg2La 的合金化和结构稳定性都最强.
王文静等[49]通过第一性原理平面波赝势方法对 Mg-Er 合金体系中MgEr、Mg2Er 和Mg24Er5 3 种中间相化合物的电子结构、形成焓、结合能进行了计算.3种化合物结合能的比较如图 2 所示,3 种中间相化合物的形成热和结合能均为负值,随着化合物中Er 成分的增加,化合物越不稳定.
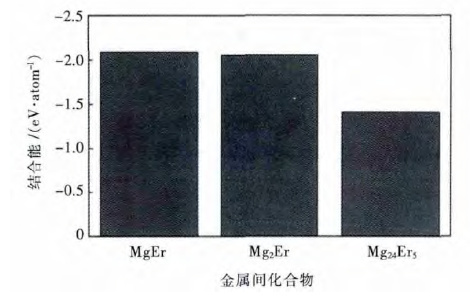 |
| 图 2 MgEr、Mg2Er 和Mg24Er5的结合能示意图 Fig. 2 Binding energy of MgEr、Mg2Er and Mg24Er5 |
此外,Yang Q 等[50]通过计算Al-La 体系相图,预测了Al4La(I4/mmm)、Al4La(Imm2)、AlLa3(Pm-3m)3 个亚稳相存在,并计算了体系中存在的所有振动常数,邹祥宇等[51]利用第一性原理CASTEP 软件包计算了Al3Sc 的晶体结构和电子结构.计算得到Al3Sc 晶格常数为a=0.411 nm,与XRD 分析结果吻合.Pang M 等[52]在第一性原理的理论支持下,重点研究了不同压强下AlSc2的内能、自由能、熵、热容随温度变化的关系(图 3).
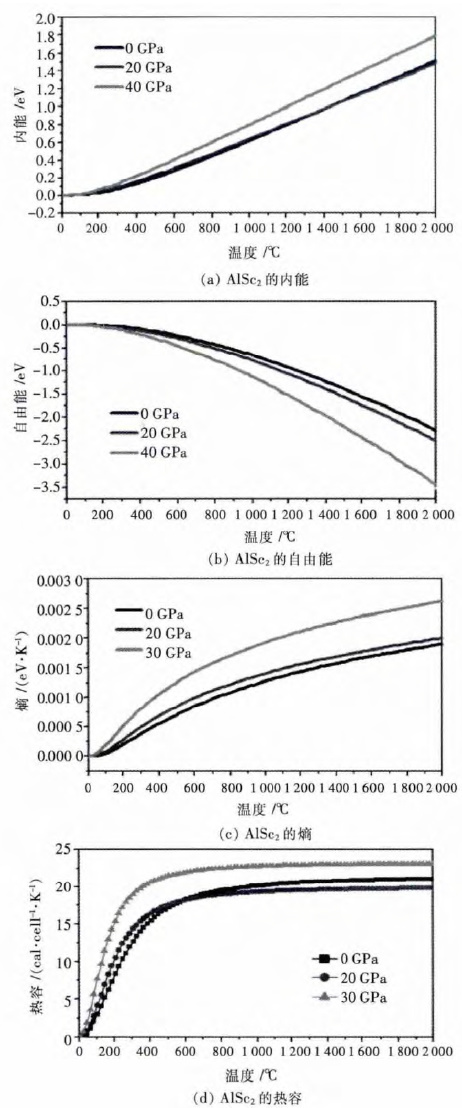 |
| 图 3 不同压强下AlSc2的热力学性质随温度的变化关系 Fig. 3 Dependence of thermodynamic properties of AlSc2 on temperature and pressure |
3.1.2 Cu 系合金
Zhang Y 等[53]对Cu-Au 二元系中化合物总能、有序无序转变温度进行了系统的预测分析,基于GGA和电子密度泛函理论,对中间相化合物Cu3Au 和 CuAu 的结构及电子结构进行了系统的计算;温玉锋等[54]在研究Fe-Cu 无序固溶体合金(Cu 原子摩尔分数分别为25 %、37.5 %和50 %) 的电子结构及基态性质时,采用了平面波投影缀加赝势和广义梯度近似相结合的方法,结果表明,FCC 型Fe-Cu 固溶体的弹性稳定性随固溶体中Cu 含量的增加而增强,后2 种成分的合金以亚稳态形式存在于合金相中.Cheng H等[55]利用于密度泛函理论,对Cu11In9的各项性质进行了计算,结果表明,Cu11In9具有低弹性各向异性,低硬度、高韧性和良好的电导率;Du J 等[56]采用第一性原理研究了Cu-Zr 体系中间相化合物的结构和性质,研究发现,计算所得8 种中间相化合物形成焓均为负值,机械稳定性高,其中CuZr2是半金属隙为0.227 eV 的半金属导体,其余均为导体;Zhang Y等[57]基于第一性原理,研究了Cu-Sb-Se 三元体系的相稳定性,发现中间相化合物Cu4SbSe5在300 K 以下稳定存在,Cu3SbSe3高温下不稳定,易转变成新的中间相Cu12Sb4Se13,并预测了Cu12Sb4Se13的市场应用前景.
3.1.3 W 系合金WC-Co 硬质合金及W 具有熔点高、硬度高、耐磨、耐腐蚀等优点,被广泛应用航空航天、机械加工、冶金、石油钻井、矿山工具、电子工业等领域.作为金属基复合材料的钨铜合金,兼具钨的高温稳定性和铜良好的导热导电性能,在其基础上发展起来的发汗材料等新型功能材料已显现出重要的应用价值.钨铜合金制备方法单一,一般只能由粉末冶金的方法获得,因此,从钨铜合金的结构及热力学性质出发,来研究其成相机理,已成为当下钨铜合金研究的重点内容之一.
庞梦德[58]为优化C-Co-W-Nb 四元系,采用第一性原理分别计算了该体系中各中间相在0 K 温度下的形成焓,计算结果能够很好的与实验值相吻合.梁超平[60]基于密度泛函理论的VASP 软件,采用第一性原理计算方法,对钨铜合金的热力学性能及相的稳定性进行了深入研究,结果表明,所有W100-xCux的形成焓均为正值,这也验证了相图学上钨铜完全不互溶这本质属性;翟东等[61]在对钨铜合金高温高压性质的研究中,基于第一性原理理论计算的方法,分别采用准谐德拜和准简谐近似模型计算了该体系中3 种合金Cu3W,CuW 和CuW3的热容随温度的变化关系,并综合讨论了压强与相对体积的关系;得出如下结论: 在高温区域内,2 种计算方法所得热容都与Dulong-Petit 极限nNAkB 基本相符,3 种合金的相对体积与压强成反比关系,且随着温度的升高,反比趋势更加显著.
另外,黄多辉等[59]在准谐近似理论的前提下,使用第一性原理的方法,研究了立方结构型W 的熵(S)、振动自由能(F)、等压热容(CP)和等容热容(CV)等热力学性质随温度变化的关系.研究结果表明,在0~2 000 K 时,S、F、CP 等与实验值几乎完全吻合;而 CV随温度的变化由于受到热电子效应的影响,在T<500 K 时,与温度成正比迅速增加,之后CV的变化逐渐趋于缓慢(图 4).
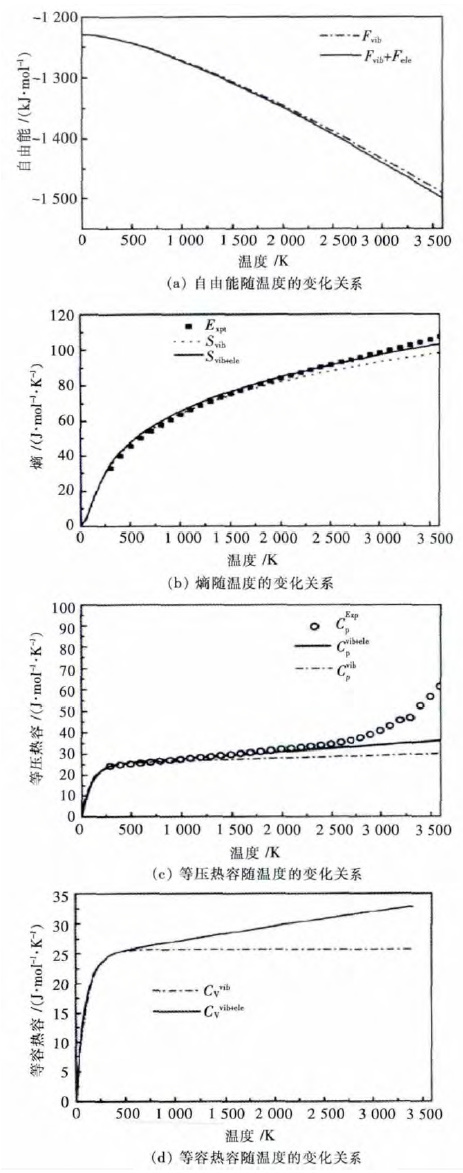 |
| 图 4 立方结构型W 在零压下的热力学性质随温度的变化 Fig. 4 Dependence of thermodynamic properties of cubic structure W on temperature under zero pressure |
采用第一性原理计算方法计算化合物的能量性质不仅仅在以上3 个方面,在Ti 合金,以及Li 合金等领域也已进行了广泛研究.例如,Tan X 等[62]在第一性原理的帮助下,对Ti-Si-N 体系的体积模量、热容和热膨胀系数等热力学性质进行了计算(如图 5),有益于Ti-Si-N 三元系的进一步研究工作的进行.
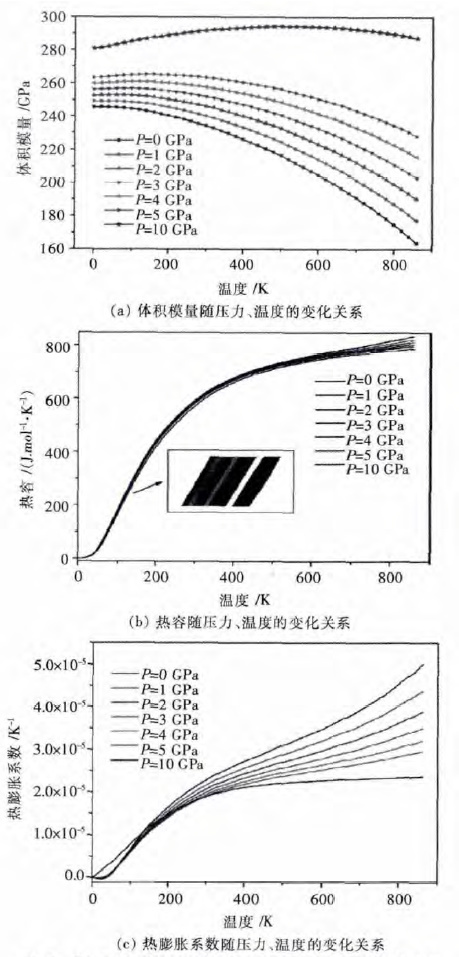 |
| 图 5 Ti-Si-N 在不同压力及温度下的热力学性质比较 Fig. 5 Dependence of thermodynamic properties of Ti-Si-N system on pressure and temperature |
3.2 相图
Am-U 体系作为Pu-U-Am 三元体系的一个重要的子二元系,对其热力学参数及性质的研究,至今无人报道,Perron A 等[63]基于第一性原理,计算了Am- U 系fcc 及bcc 相的电子结构,在此基础上,利用 CALPHAD 方法,得到Am-U 二元系相图(如图 6),为计算Pu-U-Am 三元系相图奠定了理论基础,同时为后续实验指明了方向.
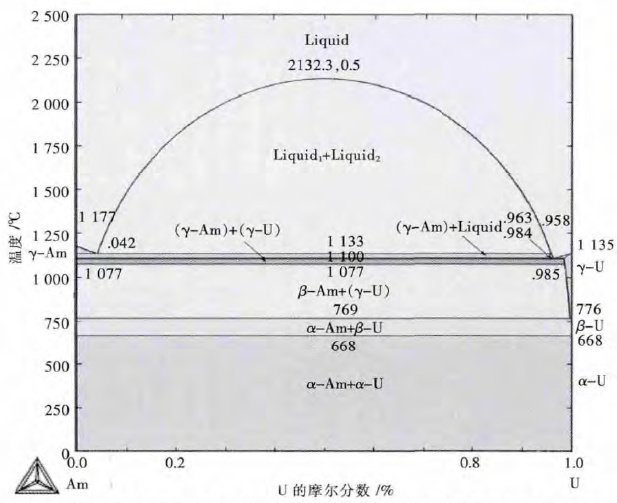 |
| 图 6 采用Ab initio 计算与CALPHAD 结合计算得到的Am-U 体系相图 Fig. 6 Phase diagram of Am-U system calculated by combination of firstprinciples calculations and CALPHAD |
Bittner R W 等[64]基于密度泛函理论对Ge-Ti 二元系中GeTi3,GeTi2,Ge3Ti5,Ge4Ti5,Ge5Ti6,GeTi 和Ge2Ti等中间相的总能进行了计算,结合X 射线衍射、包括EDX 分析在内的扫描电子显微镜及差热分析,发现了一个新的中间相Ge4Ti5的存在,并推断其形成的固态反应方程式为Ge3Ti5+Ge5Ti6=Ge4Ti5,并在上述研究的基础上对Ge-Ti 二元系相图进行了优化.Mohri T 等[65]采用第一性原理计算和集团变分法模拟计算相结合,系统的研究了以Fe 为基的Fe-Ni,Fe-Pd 和Fe-Pt 3 个二元体系的相平衡关系;
另外,在第一性原理的支持下,罗伟[66]计算得到了0 K 下该体系中9 个化合物的形成焓,结合全面评估得到的实验数据,利用CALPHAD 方法优化计算得到了该体系平衡条件下的相图.Xiong W 等[67]基于密度泛函理论,计算了Np-Zr 体系中所有稳定存在的化合物及Np、Zr 边际端的0 K 下的生成焓;利用同样的方法,Rajkumar V[68],S姚 trof J[69],Berche A等[70]分别计算了Fe-Mo、V-Zr、Gr-Ge-Mn 及Gr- Ge-Si 系相图,结果均与实验值在合理误差范围内吻合较好.
3.3 动力学性质Saunders N 和Miodownik A P 曾指出“尤其是当使用已在相平衡计算中被证明合理有效的数据时,热力学和动力学的结合是CALPHAD 方法合乎逻辑的外延”[71].其中用于动力学计算的DICTRA 软件是通过原子移动性和由热力学数据库获得的热力学因子来描述各种扩散系数随温度和成分的变化规律,原子移动性参数只能通过实测扩散系数进而优化得到,且测定扩散系数的各实验方法均存在较大的局限性,因此,运用第一性原理计算方法,计算包括自扩散系数、互扩散系数及杂质扩散系数在内的动力学性质迅速引起了国内外学者的广泛关注.
Mantina M 等[72]运用第一性原理计算了纯Al 的自扩散系数,计算结果与实测数据十分吻合;Sandberg N 等[73]基于相同的原理,对ɑ-Fe 进行了研究计算,计算结果与实验结果的比较如图 7;Van der Ven A 等[74]借助第一性原理的帮助,研究了600 K 温度下Al-Li的互扩散系数;基于相同的方法,Ganeshan S 等[75]做了关于稀镁合金内的杂质扩散系数的计算,计算结果与实验值在误差范围内吻合很好.
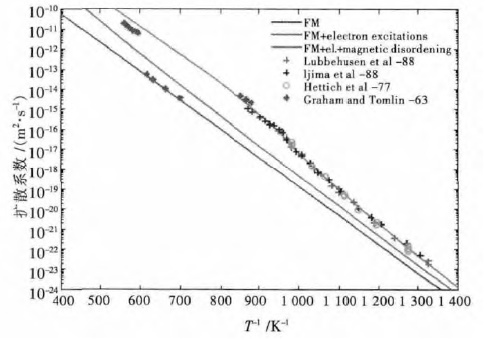 |
| 图 7 ɑ-Fe 自扩散系数的第一性原理计算与实验结果比较 Fig. 7 Comparison between first-principle calculation for self diffusion coefficients of ɑ-Fe and experimental result |
4 结论
第一性原理与CALPHAD 的结合是目前相图及热力学研究的热点领域.第一性原理从微观电子层面解释了晶格稳定性影响因素,阐述了结构、性质的作用机理,得到化合物的形成焓、固溶体的混合焓、结合能、相变热等体系所需能量性质,为CALPHAD 提供了理论数据支持,促进了CALPHAD 技术的发展.然而,合金或化合物中存在元素间的相互作用,第一性原理计算仅从纯元素理论分析外推得到,难免会存在一定程度的偏差,需考虑影响实际结构的影响因子;而且,第一性原理的计算进度通常较缓慢,为了快速的获得计算结果,经常会人为的加入部分经验参数,从而影响了结果的准确度.相信随着第一性原理计算理论的进一步完善和计算机科学的发展,第一性原理计算将会获得更加精确的热力学性质,将会为相图计算的研究发挥更大的作用.
| [1] | 乔芝郁, 郝士明. 相图计算研究的进展[J]. 材料与冶金学报, 2005, 4(2): 83–90. |
| [2] | 郭景坤. 陶瓷晶界应力设计[J]. 无机材料学报, 1995, 10(1): 27–31. |
| [3] | Saunders N, Miodownik A P. CALPHAD (calculation of phase diagrams): A comprehensive guide[M]. Elsevier: Elsevier , 1998. |
| [4] |
Ye X Y, Zhang J, Wang Y, et al. Optimization and calculation of the LaBr3-MBr (M= Na, K, Rb, Cs) phase diagrams[J].
Calphad, 2004, 28(2): 147–151. DOI: 10.1016/j.calphad.2004.07.006. |
| [5] |
Ye X Y, Zhang J, Sun Y M, et al. Thermodynamic optimization of TmCl3-ACl (A= Na, K, Rb, Cs) phase diagrams[J].
Rare Earths, 2005, 23(1): 88–92. |
| [6] |
Ye X Y, Sun Y M, Zhang J, et al. Thermodynamic optimization of DyCl3-NaCl system[J].
Journal of Shanghai University (English Edition), 2005, 9(3): 279–282. DOI: 10.1007/s11741-005-0093-z. |
| [7] |
Ye X Y, Zhuang W D, Deng C Y, et al. Thermodynamic investigation on the Al2O3-BaO binary system[J].
Calphad, 2006, 30(3): 349–353. DOI: 10.1016/j.calphad.2005.12.004. |
| [8] |
Ye X Y, Zhuang W D, Wang J F, et al. Thermodynamic description of SrO-Al2O3 system and comparison with similar systems[J].
Journal of Phase Equilibria and Diffusion, 2007, 28(4): 362–368. DOI: 10.1007/s11669-007-9086-x. |
| [9] |
Tao X, Ouyang Y, Liu H, et al. Abinitio calculation of the total energy and elastic properties of Laves phase C15 Al2RE (RE= Sc, Y, La, Ce-Lu)[J].
Computational Materials Science, 2008, 44(2): 392–399. DOI: 10.1016/j.commatsci.2008.03.036. |
| [10] | Kaufman L, Bernstain H. Computer calculation of phse diagram[M]. New York: Academic Press , 1970. |
| [11] | Hillert M. Phase equilibria, phase diagram and phase transformations[M]. Cambridge University: Cambridge , 1998. |
| [12] |
Segall M D, Lindan P J D, Probert M J, et al. First-principles simulation: Ideas, illustrations and the CASTEP code[J].
Journal of Physics: Condensed Matter, 2002, 14(11): 2717. DOI: 10.1088/0953-8984/14/11/301. |
| [13] | 谢希德, 陆栋. 固体能带理论[M]. 上海: 复旦大学出版社 , 1998. |
| [14] |
Fermi E. Eine statistische methode zur bestimmung einiger eigenschaften des atoms und ihre anwendung auf die theorie des periodischen systems der elemente[J].
Zeitschrift für Physik, 1928, 48(1/2): 73–79. |
| [15] |
Kohn W. Nobel lecture: Electronic structure of matter-wave functions and density functionals[J].
Reviews of Modern Physics, 1999, 71(5): 1253–1266. DOI: 10.1103/RevModPhys.71.1253. |
| [16] |
Kohn W, Sham L J. Quantum density oscillations in an inhomogeneous electron gas[J].
Physical Review, 1965, 137(6A): A1697–A1705. DOI: 10.1103/PhysRev.137.A1697. |
| [17] | Thomas L H. The calculation of atomic fields[C]// Cambridge: Cambridge University Press, 1927: 542-548. |
| [18] |
Hohenberg P, Kohn W. Inhomogeneous electron gas[J].
Physical Review, 1964, 136(3B): B864. DOI: 10.1103/PhysRev.136.B864. |
| [19] |
Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects[J].
Physical Review, 1965, 140(4A): A1133–A1138. DOI: 10.1103/PhysRev.140.A1133. |
| [20] |
Slater J C. A simplification of the Hartree-Fock method[J].
Physical Review, 1951, 81(3): 385–391. DOI: 10.1103/PhysRev.81.385. |
| [21] |
Ceperley D M, Alder B J. Ground state of the electron gas by a stochastic method[J].
Physical Review Letters, 1980, 45(7): 566–573. DOI: 10.1103/PhysRevLett.45.566. |
| [22] |
Perdew J P, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems[J].
Physical Review B, 1981, 23(10): 5048–5079. DOI: 10.1103/PhysRevB.23.5048. |
| [23] |
Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J].
Physical review letters, 1996, 77(18): 3865–3868. DOI: 10.1103/PhysRevLett.77.3865. |
| [24] |
Perdew J P, Kurth S, Zupan A, et al. Accurate density functional with correct formal properties: A step beyond the generalized gradient approximation[J].
Physical review letters, 1999, 82(12): 2544–2549. DOI: 10.1103/PhysRevLett.82.2544. |
| [25] |
Lee C, Yang W, Parr R G. Development of the colle-salvetti correlation-energy formula into a functional of the electron density[J].
Physical review B, 1988, 37(2): 785–796. DOI: 10.1103/PhysRevB.37.785. |
| [26] |
X G. First-principles responses of solids to atomic displacements and homogeneous electric fields: Implementation of a conjugate-gradient algorithm[J].
Physical Review B, 1997, 55(16): 10337–10354. DOI: 10.1103/PhysRevB.55.10337. |
| [27] |
X G. A brief introduction to the ABINIT software package[J].
Zeitschrift für Kristallographie, 2005, 220(5/6): 558–562. |
| [28] |
Gonze X, Amadon B, Anglade P M, et al. ABINIT: First-principles approach to material and nanosystem properties[J].
Computer Physics Communications, 2009, 180(12): 2582–2615. DOI: 10.1016/j.cpc.2009.07.007. |
| [29] | Martin R M. Electronic structure: basic theory and practical methods[M]. Cambridge : Cambridge University Press , 2004. |
| [30] |
Kresse G, Furthmüller J. Software VASP, vienna (1999)[J].
Physics Review B, 1996, 54(11): 169. |
| [31] |
Soler J M, Artacho E, Gale J D, et al. The SIESTA method for ab initio order -N materials simulation[J].
Journal of Physics: Condensed Matter, 2002, 14(11): 2745–2779. DOI: 10.1088/0953-8984/14/11/302. |
| [32] |
Schwarz K, Blaha P, Madsen G K H. Electronic structure calculations of solids using the WIEN2k package for material sciences[J].
Computer Physics Communications, 2002, 147(1): 71–76. |
| [33] |
Van de Walle A, Asta M, Ceder G. The alloy theoretic automated toolkit: A user guide[J].
Calphad, 2002, 26(4): 539–553. DOI: 10.1016/S0364-5916(02)80006-2. |
| [34] |
Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method[J].
Physical Review B, 1999, 59(3): 1758–1775. DOI: 10.1103/PhysRevB.59.1758. |
| [35] |
Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].
Physical Review B, 1990, 41(11): 7892–7895. DOI: 10.1103/PhysRevB.41.7892. |
| [36] |
Wood D M, Zunger A. A new method for diagonalising large matrices[J].
Journal of Physics A: Mathematical and General, 1985, 18(9): 1343–1359. DOI: 10.1088/0305-4470/18/9/018. |
| [37] |
Davidson E R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices[J].
Journal of Computational Physics, 1975, 17(1): 87–94. DOI: 10.1016/0021-9991(75)90065-0. |
| [38] |
Pulay P. Convergence acceleration of iterative sequences. The case of SCF iteration[J].
Chemical Physics Letters, 1980, 2: 73. |
| [39] |
Pulay P. Improved SCF convergence acceleration[J].
Journal of Computational Chemistry, 1982, 3(4): 556–560. DOI: 10.1002/(ISSN)1096-987X. |
| [40] |
D J D. Modified Broyden's method for accelerating convergence in self-consistent calculations[J].
Physical Review B, 1988, 38(18): 12807–12812. DOI: 10.1103/PhysRevB.38.12807. |
| [41] |
Kaufman L, Turchi P E A, Huang W, et al. Thermodynamics of the Cr-T-W system by combining the Ab initio and CALPHAD method[J].
Calphad, 2001, 25(3): 419–433. DOI: 10.1016/S0364-5916(01)00061-X. |
| [42] | Colinet C. Phase diagram calculations: contribution of ab initio and cluster variation methods[M].USA: 2002. |
| [43] | 陈星秋, 严新林, 丁学勇, 等. 化合物生成焓:一百年和密度泛函基量子机制的原子模型新时代[J]. 中国稀土学报, 2004, 22: 1–7. |
| [44] | 赵燕燕. Ag-Cu-Ni-Ce合金系二元稀土化合物的第一性原理计算研究[D]. 重庆: 重庆理工大学, 2014. |
| [45] | 赵沙斐, 潘荣凯, 周思晨, 等. Al4Ce和Al2CeZn2相弹性性能的第一性原理研究[J]. 郑州大学学报(工学版), 2014(2): 104–107. |
| [46] | 曾梦雪. Mg2Y(Ca)和tl26型Mg12RE合金的弹性性能与电子结构研究[D]. 南宁: 广西大学, 2012. |
| [47] | 苏昕. 稀土镁合金的第一性原理计算及组织性能研究[D]. 上海: 上海交通大学, 2013. |
| [48] |
Chen G, Zhang P. First-principles study of electronic structures, elastic properties and thermodynamics of the binary intermetallics in Mg-Zn-Re-Zr alloy[J].
Defence Technology, 2013, 9(3): 131–139. DOI: 10.1016/j.dt.2013.09.011. |
| [49] | 王文静, 刘子利, 刘希琴, 等. Mg-Er金属间化合物稳定性与电子结构的第一性原理研究[J]. 中国有色金属学报, 2014, 24(2): 7–9. |
| [50] |
Yang Q, Liu X, BU F, et al. First-principles phase stability and elastic properties of Al-La binary system intermetallic compounds[J].
Intermetallics, 2015, 60: 92–97. DOI: 10.1016/j.intermet.2015.02.007. |
| [51] | 邹祥宇, 廖先杰, 卫学玲, 等. Al3Sc的FFC法制备和第一性原理计算研究[J]. 材料与冶金学报, 2014, 13(4): 284–287. |
| [52] |
Pang M, Zhan Y, Wang H, et al. Ab initio investigation of structural, electronic, mechanical, and thermodynamic properties of AlSc2 intermetallic compound under pressure[J].
Journal of Applied Physics, 2011, 110(3): 33533–33534. DOI: 10.1063/1.3622340. |
| [53] |
Zhang Y, Kresse G, Wolverton C. Nonlocal first-principles calculations in Cu-Au and other intermetallic alloys[J].
Physical Review Letters, 2014, 112(7): 75502–75503. DOI: 10.1103/PhysRevLett.112.075502. |
| [54] | 温玉锋, 孙坚, 黄健. 基于特殊准随机结构模型的FCC Fe-Cu无序固溶体合金的弹性稳定性[J]. 中国有色金属学报, 2012, 22(9): 2522–2528. |
| [55] |
Cheng H C, Yu C F, Chen W H. Physical, mechanical, thermodynamic and electronic characterization of Cu11In9 crystal using first-principles density functional theory calculation[J].
Computational Materials Science, 2014, 81: 146–157. DOI: 10.1016/j.commatsci.2013.07.039. |
| [56] |
Du J, Wen B, Melnik R, et al. Phase stability, elastic and electronic properties of Cu-Zr binary system intermetallic compounds: A first-principles study[J].
Journal of Alloys and Compounds, 2014, 588: 96–102. DOI: 10.1016/j.jallcom.2013.11.018. |
| [57] |
Zhang Y, Ozolins V, Morelli D, et al. Prediction of new stable compounds and promising thermoelectrics in the Cu-Sb-Se system[J].
Chemistry of Materials, 2014, 26(11): 3427–3435. DOI: 10.1021/cm5006828. |
| [58] | 庞梦德. Be-Sr, Be-Mg二元系和C-Co-W-Nb四元系的热力学研究[D]. 长沙: 中南大学, 2014. |
| [59] | 黄多辉, 李强, 曹启龙, 等. W热力学性质和弹性性质的第一性原理研究[J]. 稀有金属材料与工程, 2013, 42(9): 1849–1853. |
| [60] | 梁超平. 若干过渡族金属及合金系统关键性能的第一性原理研究[D]. 长沙: 中南大学, 2013. |
| [61] | 翟东, 韦昭, 冯志芳, 等. 铜钨合金高温高压性质的第一性原理研究[J]. 物理学报, 2014, 63(20): 206501. |
| [62] |
Tan X, Wang Y, Jia Y, et al. Ab-initio study of the structure and thermodynamic properties of Ti-Si-N at external pressure[J].
Computational Materials Science, 2015, 96: 33–38. DOI: 10.1016/j.commatsci.2014.08.041. |
| [63] |
Perron A, Turchi P E A, Landa A, et al. The Pu-U-Am system: An ab initio informed CALPHAD thermodynamic study[J].
Journal of Nuclear Materials, 2015, 458: 425–441. DOI: 10.1016/j.jnucmat.2014.12.101. |
| [64] |
Bittner R W, Colinet C, Tedenac J C, et al. Revision of the Ge-Ti phase diagram and structural stability of the new phase Ge4Ti5[J].
Journal of Alloys and Compounds, 2013, 577: 211–216. DOI: 10.1016/j.jallcom.2013.04.114. |
| [65] |
Mohri T, Chen Y. First-principles investigation of L10-disorder phase equilibria of Fe-Ni,-Pd, and -Pt binary alloy systems[J].
Journal of Alloys and Compounds, 2004, 383(1): 23–31. |
| [66] | 罗伟. Ga-Zr和Co-Cr-Nb体系的相图测定和热力学计算[D]. 长沙: 中南大学, 2014. |
| [67] |
Xiong W, Xie W, Morgan D. Thermodynamic evaluation of the Np-Zr system using CALPHAD and ab initio methods[J].
Journal of Nuclear Materials, 2014, 452(1): 569–577. |
| [68] |
Rajkumar V B, Kumar K C H. Thermodynamic modeling of the Fe-Mo system coupled with experiments and ab initio calculations[J].
Journal of Alloys and Compounds, 2014, 611: 303–312. DOI: 10.1016/j.jallcom.2014.05.030. |
| [69] |
Štrof, J, Pavlů J, Wdowik U D, et al. Laves phases in the V-Zr system below room temperature: Stability analysis using ab initio results and phase diagram[J].
Calphad, 2014, 44: 62–69. |
| [70] |
Berche A, Tédenac J C, Jund P. Ab-initio calculations and CALPHAD description of Cr-Ge-Mn and Cr-Ge-Si[J].
Calphad, 2015, 49: 50–57. DOI: 10.1016/j.calphad.2015.02.004. |
| [71] | Saunders N, Miodownik A P. Calculation of phase diagrams (CALPHAD): a comprehensive guide[M]. Elsevier: Elsevier , 1998. |
| [72] |
Mantina M, Wang Y, Arroyave R, et al. First-principles calculation of self-diffusion coefficients[J].
Physical Review Letters, 2008, 100(21): 215901–215904. DOI: 10.1103/PhysRevLett.100.215901. |
| [73] |
Sandberg N, Chang Z, Olsson P, et al. Modeling of the magnetic free energy of self-diusion in bcc Fe[J].
Physical Review B, 2015, 75(2): 1–8. |
| [74] |
Van der Ven A, Ceder G. First principles calculation of the interdiffusion coefficient in binary alloys[J].
Physical Review Letters, 2005, 94(4): 45901. DOI: 10.1103/PhysRevLett.94.045901. |
| [75] |
Ganeshan S, Hector L G, Liu Z K. First-principles calculations of impurity diffusion coefficients in dilute Mg alloys using the 8-frequency model[J].
Acta Materialia, 2011, 59(8): 3214–3228. DOI: 10.1016/j.actamat.2011.01.062. |
 2015, Vol. 6
2015, Vol. 6


