| 某矿露天残采爆破振动对临近尾矿坝稳定性的影响分析 |
b. 江西理工大学 矿业工程重点实验室 ,江西 赣州 341000
b. Jiangxi University of Science and Technology Key Laboratory of Mining Engineering, Ganzhou 341000, China
我国是一个矿业大国,目前每年的尾矿排放量至少在6亿t以上,除小部分作为矿山充填或综合利用外,绝大部分要堆存于尾矿库.尾矿库的正常运行,不仅关系到一个矿山企业的经济效益,而且与库区下游居民的生命财产及周边环境息息相关,坝体一旦溃堤,对下游居民的生命财产造成严重威胁,也将给企业带来不可估量的损失[1].因此,对于尾矿坝的稳定性分析有着十分重要的现实意义.
露天残矿开采在尾矿坝附近的情况较少,其爆破作业对尾矿坝稳定性产生影响的可能性较大[2-3].在爆破作业的同时,尾矿库扩容加高的二期工程,也必须开展尾矿坝的稳定性分析.一旦坝体破坏滑裂,将会造成严重的损失,影响尾矿库二期扩容工程的顺利进行[4].因此,进行露天残采爆破振动对临近尾矿坝稳定性的影响研究,对尾矿库的安全运行和二期扩容工程有着重要的指导意义.
目前,尾矿坝稳定性分析计算中常用的方法是有限元极限平衡法[5].此方法能较好地结合有限元应力分析方法和极限平衡法的特点,由弹塑性有限元分析手段,结合整体的应力场的影响,随后以优化搜索方法确定最危险滑动面的位置及其安全系数.有限元极限平衡法理论体系严密,计算效率高,是尾矿坝坝体稳定性评价的重要手段 [6~8].
本文以某尾矿库为例,在现场爆破振动测试的基础上,对现阶段和二期扩容后尾矿坝进行了动力稳定性计算和分析,以验证其是否符合相关规程.
1 某矿尾矿库概况该尾矿库初期坝为透水堆石坝,是在水库大坝基础上改建而成,外坡及顶面则采用石英片岩铺面,坝高29.4 m,坝顶标高160 m,坝顶宽度4.0 m,上游坡比1:1.5,下游坡比1:1.65. 后期堆积坝采用尾矿上游式堆筑而成.现阶段堆积坝外坡平均坡比为1:4.63,每3 m设一级马道,坝面上铺设了约0.40 m厚的黏性土层,并种植了植被.库内尾砂滩顶标高为205 m,尾矿堆积坝高45 m.尾矿库由左右两条狭长的V字形山谷组成,走向由东向西,地势从南往北由高变低,沟口高程为152 m左右,左沟位于库区南部,沟长约900 m,周围均是原始林地;右沟位于库区北部,沟长约850 m,其北侧为该矿露天残采矿点.
根据该矿尾矿库二期扩容工程设计,二期工程的筑坝方式依然采用上游式尾矿堆坝,从堆积标高210 m开始,坝轴线往库内平移10 m,每3 m设置一条马道,马道宽2.5 m,平均外坡坡比约1:4.67,堆积坝外坡覆人工填土0.3~0.5 m厚.右沟最终堆积标高225 m,左沟最终堆积标高240 m.
2 爆破测振试验爆破振动测试采用BlastMate Ⅲ型测振仪,可以采集P、SV及SH 3种振动体波,爆破测振布置见图 1,其中剖面1、2分别代表尾矿库的右沟和左沟剖面.测振仪布置基本与爆源呈直线,且库区测点布置在2个计算剖面上,以便将相应剖面上的爆破振动信号用于后期尾矿坝稳定性数值计算.
本次爆破方式为中深孔爆破,孔深约10 m,每次爆破测试布置5个测点,共进行3次测试.测振仪与爆源及测振仪与测振仪之间间隔一定距离,各个测点的坐标由手持式GPS仪卫星定位获取,并以皮尺测距加以校核.其中4、5测点分别布置在剖面1、2上.
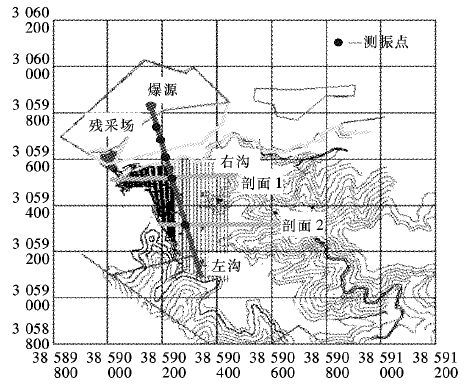 |
| 图 1 爆源及测振仪布置平面图 Fig. 1 Plan of Explosion Source and Vibrometer Layout |
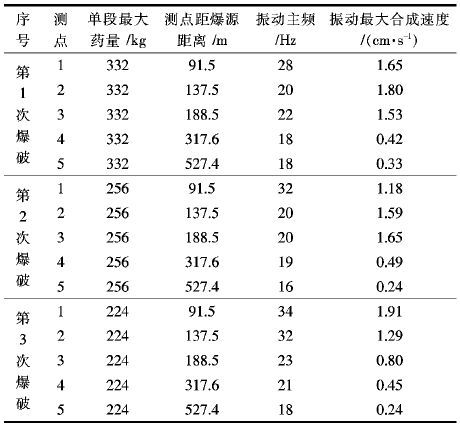
爆破振动测试试验完成后,导出测振数据,得到测点振动最大合成速度,结果见表 1.
| 表1 爆破测振结果 Table 1 Blasting vibration results |
 |
| 点击放大 |
根据《爆破安全规程》(GB6722-2011) ,爆破振动最大振速(萨道夫斯基公式)公式为:
| $V=K{{\left( \frac{{{Q}^{1/3}}}{R} \right)}^{\alpha }}$ | (1) |
式(1) 中:Q为炸药量(kg),R为爆源至测点间距离(m),K和a为与爆破点地形、地质条件有关的系数和衰减指数.
利用最小二乘法,采用表 1中的测振数据拟合式(1) 中的待定参数K和a,结果为K=107.32,a=1.376.所以露天残采爆源至尾矿库区间的爆破振动最大振速公式为:
| $V=105.32{{\left( \frac{{{Q}^{1/3}}}{R} \right)}^{1.376}}$ | (2) |
现场调查可知,露天残采采矿点距离现阶段及二期扩容后尾矿坝最近处约110 m,根据公式(2) ,计算得到单段药量最大332 kg时爆破,最近处质点振速为2.344 cm/s. 尾矿坝作为工业建筑物,查询《爆破安全规程》(GB6722-2011) ,振动主频在10~50 Hz时爆破振动安全允许标准为3.5~4.5 cm/s.因此计算得到的质点振速小于标准值范围,露天残采爆破满足安全规程要求.
3 爆破振动对尾矿坝稳定性的影响根据现场爆破测振试验,进一步结合数值模拟方法开展爆破振动对尾矿坝坝体稳定性的影响模拟与分析.
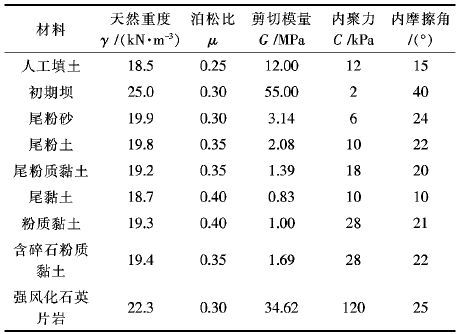
3.1 计算模型 3.1.1 物理力学参数根据该矿尾矿库勘察报告,选取的物理力学参数见表 2.
| 表2 物理力学参数 Table 2 Physical and mechanical parameters |
 |
| 点击放大 |
3.1.2 边界条件
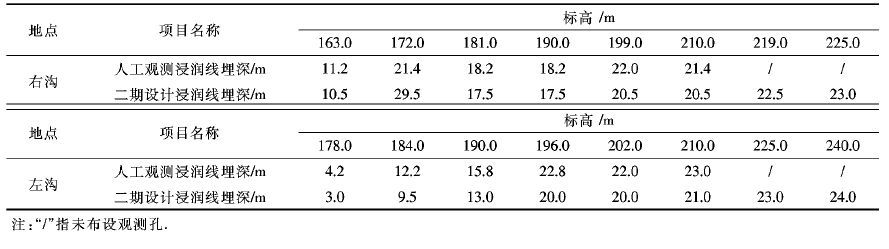
该尾矿库模型的边界条件包括位移边界条件和水位边界条件.其中位移边界条件为模型两侧的水平位移约束和底部的粘黏滞约束;水位边界条件为坝体浸润线[9~-11]位置.为了解坝体内浸润线的位置和变化情况,设置了浸润线人工观测孔进行定期观测,根据长期观测数据资料以及人工观测孔与剖面的相对位置,从而确定剖面的浸润线埋深,见表 3.
| 表3 不同标高处的浸润线埋深 Table 3 Depth of phreatic line |
 |
| 点击放大 |
3.1.3 模型建立
根据计算剖面、边界条件与材料物理力学参数,应用岩土软件Geo-Studio建立的现阶段尾矿坝稳定性计算模型见图 2、图 3.
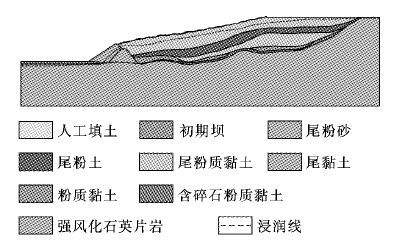 |
| 图 2 剖面1计算模型 Fig. 2 Computational model of section 1 |
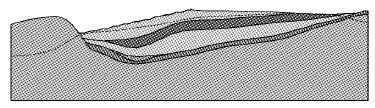 |
| 图 3 剖面2计算模型 Fig. 3 Computational model of section 2 |
根据该矿尾矿库二期扩容工程设计资料,建立的二期扩容后尾矿坝稳定性计算模型见图 4、图 5.
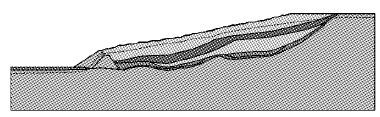 |
| 图 4 二期剖面1计算模型 Fig. 4 Computational model of section 1 in stage Ⅱ |
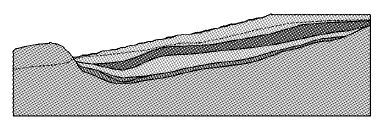 |
| 图 5 二期剖面2计算模型 Fig. 5 Computational model of section 2 in stageⅡ |
3.2 爆破振动信号
数值计算采用Geo-studio有限元软件的动力学Quake/W模块.计算时由于爆源在剖面线的正北方,第1次爆破的单段炸药量最大,因此,主要考虑第1次爆破测得的SH波(方向垂直于坝体)和SV波(方向平行于坝体)对坝体的影响[12~-15].
其中两剖面测振点处的爆破振动信号用于现阶段和二期扩容后尾矿坝稳定性计算.其露天爆破在2个剖面测振点处的振动波形见图 6、图 7.
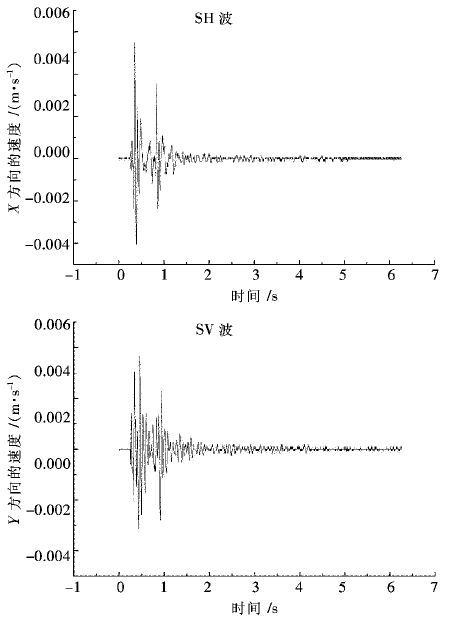 |
| 图 6 剖面1处SH、SV波振动波形 Fig. 6 Vibration waveform of SH and SV wave in Section 1 |
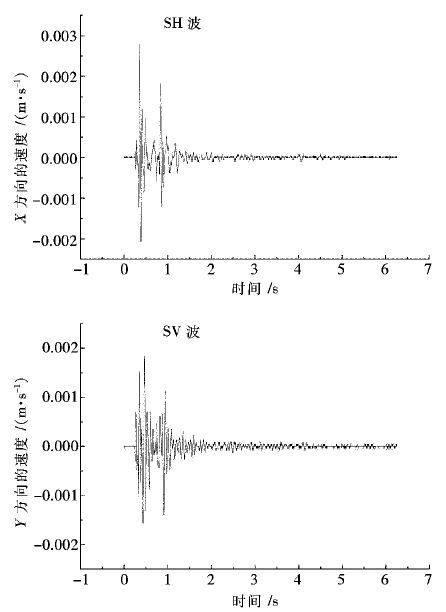 |
| 图 7 剖面2处SH、SV波振动波形 Fig. 7 Vibration waveform of SH and SV wave in Section 2 |
3.3 爆破振动对现阶段尾矿坝稳定性的影响分析
图 6、图 7中的爆破振动波形以速度的形式加载至现阶段尾矿库剖面1、2处.当Quake/W动力学模块完成尾矿坝振动计算后,将计算结果导入Geo-studio软件的Slope/W模块,采用Newmark Deformation 方法计算分析尾矿坝的稳定性,得到现阶段尾矿坝振动安全系数随时间的变化见图 8、图 9.
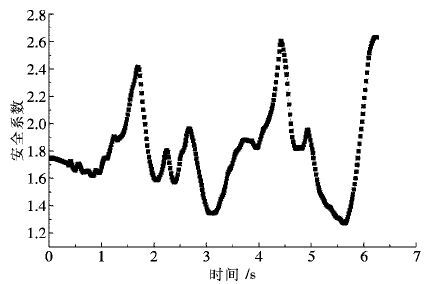 |
| 图 8 剖面1安全系数随时间的变化 Fig. 8 Changes of safety factor of section 1 vs time |
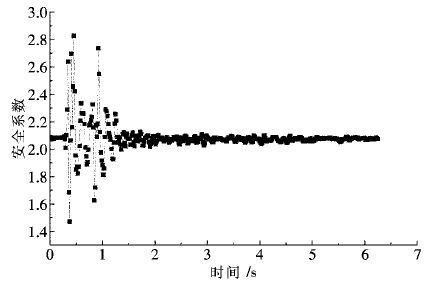 |
| 图 9 剖面2振动安全系数随时间的变化 Fig. 9 Changes of safety factor of section 2 vs time |
由图 8、图 9可知,在爆破振动情况下,现阶段尾矿库剖面1的最小安全系数为1.273,剖面2的最小安全系数为1.471.
3.4 爆破振动对二期扩容后尾矿坝稳定性的影响分析同样以图 6~图 7中的爆破振动波形以速度的形式加载至二期扩容后尾矿库剖面1、剖面2处.模拟计算方法与现阶段尾矿坝稳定性分析一致,得到二期扩容后尾矿坝振动安全系数随时间的变化见图 10、图 11.
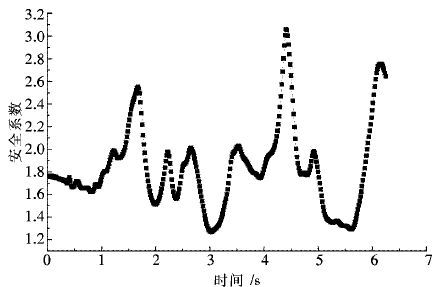 |
| 图 10 二期剖面1振动安全系数随时间的变化 Fig. 10 Changes of safety factor of section 1 vs time in stage Ⅱ |
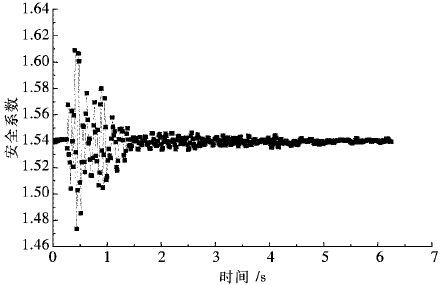 |
| 图 11 二期剖面2振动安全系数随时间的变化 Fig. 11 Changes of safety factor of section 2 vs time in stage Ⅱ |
由图 10、图 11可知,在爆破振动情况下,二期扩容后尾矿坝剖面1的最小安全系数为1.267,剖面2的最小安全系数为1.473.
由上述剖面安全系数随时间变化图可知,尾矿库的安全系数随爆破振动时间发生明显变化;剖面2比剖面1距爆源较远,其安全系数随爆破振动时间的变化趋势逐渐趋于稳定.因此,爆破振动对尾矿库的稳定性有着显著的影响;爆破振动对尾矿库的影响时间与距爆源的距离有关,距离越远,影响时间越短.
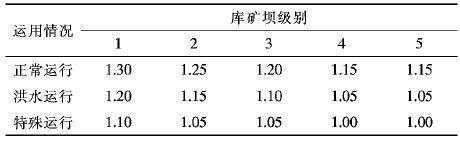
3.5 计算结果分析通过该矿尾矿库相关资料可知,现阶段尾矿坝属于三级坝,二期扩容尾矿坝属于二级坝.参考《尾矿库安全技术规程》(AQ2006-2005) ,按瑞典圆弧法计算尾矿坝抗滑稳定的安全系数不应小于表 4规定的数值.
| 表4 坝坡抗滑稳定最小安全系数 Table 4 Minimum safety factor of a stable dam against sliding |
 |
| 点击放大 |
计算结果可知,在爆破振动情况下,现阶段尾矿库右沟1剖面和左沟2剖面的最小安全系数分别为1.273和1.471,二期扩容后尾矿库右沟1剖面和左沟2剖面的最小安全系数为1.267和1.473,均大于《尾矿库安全技术规程》中规定的最小安全系数,符合安全规程.
4 结论1) 根据现场爆破测试结果,利用萨道夫斯基公式回归得到相应的K和a,计算得到爆源距尾矿坝最近处质点最大振速为2.344 cm/s,小于《爆破安全规程》(GB6722-2011) 中相应该尾矿库的爆破振动安全允许标准范围3.5~4.5 cm/s,露天残采爆破满足规程要求.
2) 爆破振动对尾矿库的稳定性有着显著的影响;爆破振动对尾矿库的影响时间与距爆源的距离有关,距离越远,影响时间越短.
3) 露天残采爆破振动对现阶段尾矿坝稳定性的影响分析表明,尾矿坝稳定性最小安全系数大于《尾矿库安全技术规程》中规定的最小安全系数,符合安全规程,尾矿库可以安全运行.
4) 露天残采爆破振动对二期扩容后尾矿坝稳定性的影响分析表明,尾矿坝稳定性最小安全系数大于《尾矿库安全技术规程》中规定的最小安全系数,符合安全规程.说明该尾矿库二的期扩容工程是可行的.
| [1] | 胡明鉴, 陈守义, 郭爱国, 等. 某上游法尾矿坝抗滑稳定性浅析[J]. 岩土力学, 2003, 24(增刊2): 254–258. |
| [2] | 李祥龙, 庙延钢, 杨溢. 爆破震动对边坡稳定性影响分析[J]. 爆破, 2006, 23(4): 15–19. |
| [3] | 赵宝云, 刘保县, 万贻平. 爆破震动对某边坡稳定性影响的数值模拟[J]. 工程地质学报, 2008, 16(1): 59–62. |
| [4] | 林国洪. 某铜矿尾矿库运行和深部开采条件下的稳定性分析[J]. 有色金属工程, 2014, 4(4): 65–67. |
| [5] | 于斯滢. 基于有限元极限平衡法的尾矿坝坝体稳定分析[D].大连:大连理工大学,2012. |
| [6] | 程灿宇, 罗富荣, 戚承志. 有限元强度折减法计算边坡稳定的对比分析[J]. 岩土力学, 2012, 33(11): 3472–3478. |
| [7] | 于斯滢, 邵龙潭, 刘士乙. 基于有限元极限平衡法的尾矿坝坝体稳定分析[J]. 岩土力学, 2013, 34(4): 1185–1190. |
| [8] |
Duncan J M. State of the art:limit equilibrium and finite-element analysis of slope[J].
Journal of Geotechnical Engineering, ASCE, 1996, 122(7): 577–596. DOI: 10.1061/(ASCE)0733-9410(1996)122:7(577). |
| [9] | 何文, 赵奎, 刘洪兴. 浸润线地质雷达探测技术在某尾矿坝稳定性分析中的应用[J]. 有色金属工程, 2014, 4(1): 68–70. |
| [10] | 梁冰, 白云鹏, 金佳旭. 库水位升高对尾矿坝稳定性的影响[J]. 水资源与水工程学报, 2010, 21(4): 11–14. |
| [11] | 宋传旺, 于广明, 王越红, 等. 基于流固耦合模型分析库水位对尾矿坝的影响[J]. 地下空间与工程学报, 2011, 7(S2增刊2): 1784–1787. |
| [12] | 吴贤振, 尹丽冰, 胡维, 等. 某矿井下浅孔毫秒延时爆破地表震动的数值模拟研究[J]. 有色金属科学与工程, 2014, 5(6): 100–104. |
| [13] | 董陇军, 李夕兵, 赵国彦, 等. 露天采矿爆破振动对砌体结构破坏效应预测的Fisher判别模型及应用[J]. 岩石力学与工程学报, 2009, 28(4): 750–756. |
| [14] | 邵良杉, 赵琳琳. 露天采矿爆破振动对民房破坏的旋转森林预测模型[J]. 中国安全科学学报, 2013, 23(2): 58–63. |
| [15] | 罗忆, 卢文波, 陈明, 等. 爆破振动安全判据研究综述[J]. 爆破, 2010, 27(1): 14–22. |
| [17] | 言志信, 彭宁波, 江平, 等. 爆破振动安全标准探讨[J]. 煤炭学报, 2011, 36(8): 1281–1284. |
 2016, Vol. 6
2016, Vol. 6


