| 毛细上升渗透系数的确定及在离子型稀土毛细上升中的应用 |
我国稀土资源丰富,其中以赣南为主要产区的稀土以“离子相”赋存,是“离子吸附型稀土矿床”,简称离子型稀土.离子型稀土是我国特有的矿产资源,具有配分齐全、高附加值元素含量高、放射性比度低、高科技应用元素多、综合利用价值大等特点,是关系国家安全和发展的最重要战略资源之一,属于国家保护性开采矿产资源,其开采工艺先后有池浸、堆浸和原地浸,目前普遍采用原地浸矿开采工艺[1-4].原地浸矿开采离子型稀土过程中伴随着严重的矿液毛细上升现象,导致稀土资源浪费和交换液损失[5].因此研究离子型稀土原地浸毛细上升对指导工程实践及原地渗流理论具有重要的意义.
毛细上升现象在许多工程中存在,例如山矿尾坝处理[6]、盐分迁移防止[7]等.毛细上升问题的研究方法主要为试验研究,马志明等[8]对不同掺和料混凝土的毛细吸力作用进行了试验研究,得出不同比例的粉煤灰会降低混凝土的吸力系数,但是可以提高混凝土的抗渗性.随后,陆文攀等[9]进一步探讨了混凝土损伤对毛细作用的影响,研究表明不同荷载形式下混凝土的毛细吸收表现为各向异性.谈云志、赵明华等[10-11]研究了毛细水上升对公路地基的影响,为研究毛细上升特点提供了很好的工程实例.以上试验研究验证了单个或多个因素对毛细作用的影响,有针对性的解决了某些工程问题.理论方面目前应用于毛细上升的模型有Brooks-Corey模型,Green-Apmt模型,Van Genuchten模型及Terzashi模型等.Brooks-Corey模型[12]确定了基质吸力和饱和度之间的经验关系.何克瑾等[13]运用Green-Apmt模型分析均匀土壤毛管水上升过程,通过室内模拟实验表明地下水补给量和毛细上升高度均与时间呈幂指数关系.在土体非均值和含水率分布不均时,杜红普等[14]在Gardner模型基础上建立多孔介质一维非饱和毛细上升模型,分析不同湿度场下的毛细吸力,得到量化毛细上升过程的理论方法.针对传统吸水和非饱和渗透模型对低含水率土预测较差的问题,张昭等[15]改进Van Genuchten模型适用性推广到全含水率范围.太沙基模型[16]是常用的毛细上升模型,假设毛细上升过程为饱和状态,在达西定律的基础上建立了毛细上升速率的预测模型.在太沙基的基础上,Lu和Liaos[17]结合Gardner的单参数模型对毛细上升速率模型进一步改进.这些模型在研究水土关系中得到了广泛应用,在研究毛细作用相关问题中具有较好的借鉴意义.
毛细作用的研究不能脱离理论的支持,在描述毛细上升过程的毛细模型中大多是用饱和渗透系数或饱和渗透系数转化的函数表示毛细上升渗透能力.试验研究表明,饱和渗透系数高估了毛细上升速率,而太沙基模型所得预测结果与实际高度具有明显的差异,其原因在于高于进气值后的毛细上升作用不再受饱和渗透系数的控制.Lu和Liaos虽然考虑渗透系数的变化改进了太沙基模型,但是模型中是用竖直向下入渗的渗透关系代替土体垂直向上对土的毛细吸力,并没有直观体现非饱和土渗透能力的参数,且空隙尺寸分布系数和表面张力系数复杂多变,一定程度上增大了模型运用的难度.
基于上述认识,本文修正太沙基模型中饱和渗透系数的取值意义,用毛细渗透系数k代替饱和渗透系数ks,并以离子型稀土为对象,通过实测数据验证修正模型的可行性,并对修正后的模型加以应用,从试验中获取毛细渗透系数的大小,在此基础上,讨论土体稀土矿土中大粒径晶体颗粒对离子型稀土毛细上升规律的影响.
1 太沙基毛细上升模型的修正 1.1 太沙基毛细上升模型太沙基在提出一维土柱毛细上升预测模型时,基于2个基本假设,一是适合饱和入渗的达西定律同样适合非饱和毛细作用;二是水力梯度表示为最大毛细上升高度和湿润锋的差与湿润峰高度的比值:
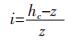
|
(1) |
式(1)中hc为最大毛细上升高度,z为湿润锋上升高度,单位为cm.取微段土柱dz,毛细流速表示为单位时间内通过土柱的流量,根据假设可得到达西公式为:
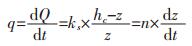
|
(2) |
式(2)中q为流速,单位为cm/h,ks为饱和渗透系数,单位为cm/h,n为孔隙率.对式(2)积分可得到毛细湿润峰位置与时间的关系式:
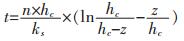
|
(3) |
太沙基假设毛细作用过程中土水关系为理想的饱和状态,模型中渗透系数值取为饱和渗透系数预测毛细上升速率.在实际应用中发现,毛细上升过程只是在进气值高度以下与太沙基模型吻合,如图 1中的BC部分,随着毛细高度的增大,AB段偏离太沙基所假设的饱和状态,此段含水率小于饱和含水率而出现不同程度的非饱和区.因此,该模型的理论结果与实际结果存在差异.
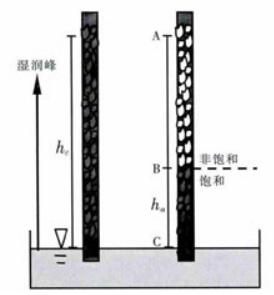 |
| 图 1 毛细上升示意图 Fig. 1 Schematic diagram of capillary rise |
1.2 模型修正
针对毛细上升中饱和渗透系数与试验事实不符的问题,用非饱和土毛细渗透系数k(下文统一简称“毛细渗透系数”)代替太沙基模型中饱和渗透系数ks,以此表征毛细上升过程的非饱和渗透能力.不改变太沙基模型中其他参数的定义,孔隙率n与饱和渗透系数ks的比值为定值,用毛细渗透系数k代替ks令作参数A,同时将难测定的参数毛细上升最大高度hc,令作参数B,即:
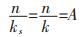
|
(4) |
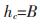
|
(5) |
式(4)中n为土柱的孔隙率,可通过实验测定,为无量纲常数,参数A单位为(cm/h)-1,参数B单位为cm.将式(4)和式(5)中的A、B代入式(3)变换可得:
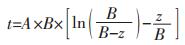
|
(6) |
毛细上升是由无数个不间断的土壤水分迁移过程组成,取小段土柱dz,湿润峰z是t的函数,对式(6)微分可得毛细上升速率与毛细上升高度的关系式:
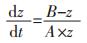
|
(7) |
模型的修正主要从不同粒径级配和孔隙率来研究毛细上升过程的规律.根据已知时间-毛细上升高度的函数关系,通过试验数据结合修正模型式(6)拟合毛细渗透系数、拟合的最大毛细上升高度可作为定义稀土毛细作用大小的重要参数.
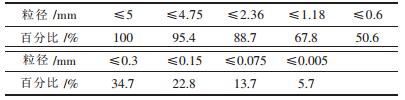
2 离子型稀土毛细上升试验 2.1 试样试样为离子型稀土,取自寻乌某离子型稀土矿,其级配如表 1所示.将土样碾碎过4.75 mm的筛分仪筛除大颗粒土,置室内恒温环境风干后拌匀,按粒径d≤4.75 mm、d≤1.18 mm、d≤0.6 mm、d≤0.3 mm(下文简称为最大粒径4.75、1.18、0.6、0.3,单位mm)筛选分组.参考2007版《公路土工试验规程》,用灌水法测得土样的相对密度,以便计算不同密度土柱的孔隙率n.采用定水头法测定4种土样的饱和渗透系数.
| 表1 稀土样粒径级配参数 Table 1 Particle size parameters of ionic rare earth specimens |
 |
| 点击放大 |
2.2 试验装置
实验室内自制毛细上升试验装置,该装置由透明有机玻璃管(下文简称主管)、水槽、铁架台组成,如图 2所示.
 |
| 图 2 试验装置图 Fig. 2 Testing apparatus |
主管外径为25 mm,内径20 mm,长2 000 mm.为避免试验时土样漏入水槽,同时不影响水的毛细作用,主管底端用38 μm的滤布绑扎.为准确读取毛细上升高度,沿管壁轴线方向贴有精度为1 mm的刻度尺.水槽用耐腐蚀的不锈钢制成,水槽内外皆有刻度,精度为1 mm.水槽一端预留10 mm的小洞,以保证内部水面的恒定.铁架台用于固定主管.
2.3 试验方法试验主要步骤分为:筛土、装土、固定土柱、通入溶液、记录数据5步.为保证土样充填均匀密实,采用分层震荡击实的方法,通过固定刻度段加同等质量的土来实现主管中土样的均实性;装土完毕后将土柱固定到铁架台,根据容器刻度所拉水平线进行绑定,保证土柱保持在同一高度;管端入水深度固定,通过补水和溢水装置保证管端水头压力为定值.
试验溶液为清水,毛细上升高度根据湿润峰来确定.从土水两相接触瞬间开始计时,根据毛细水上升过程中土体含水率变化引起土柱色差来判断水分迁移的距离,读取湿润峰位置.4组土样同时进行试验和读取试验数据.
对每种最大粒径情况分别同时进行3个试验,以保证试验具有一定的精度和可重复性.
2.4 试验结果由于篇幅所限,对每种最大粒径情况的3个试验仅选取一个试验数据进行分析.图 3为试验得到的4组粒径土样毛细上升高度与时间的关系曲线.由图 3可以看出,4组土样的毛细上升高度随时间的变化趋势一致,先是快速上升,然后缓慢上升.土样粒径不同,相同清水在稀土中的毛细上升高度随时间的变化轨迹不同;相同时刻,土体粒径越大,毛细上升高度越小,这表明土体大颗粒晶体的增加对毛细上升现象有重要的影响.
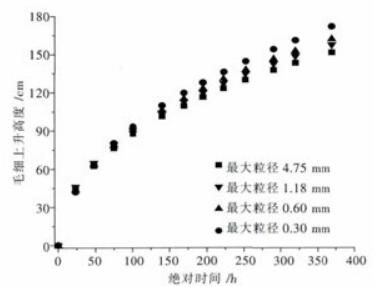 |
| 图 3 毛细上升高度与时间的关系 Fig. 3 The relation between capillary rise height and time |
图 4为毛细上升速率随时间的变化关系.由图 4可以看出,4组土样毛细上升速率整体变化趋势一致.土水接触的瞬间,毛细上升速率较快,随后毛细速率快速减小.前10 h内速率变化幅度较大,速率从8 cm/s骤减到1 cm/s左右;100 h后,速率减小到0.3 cm/h左右.在试验的时间段内,最后的毛细上升速率变化小,稳定在0.1~0.2 cm/h区间内.
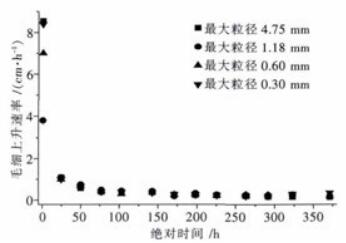 |
| 图 4 毛细上升速率与时间的关系 Fig. 4 The relation between capillary rise velocity and time |
3 毛细渗透能力的讨论 3.1 毛细渗透系数的确定
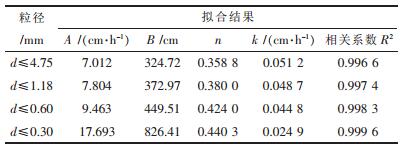
为了确定非饱和离子型稀土的毛细上升能力,用修正后的太沙基模型式(6)拟合毛细渗透系数.同时用图 3所示的毛细上升高度与时间关系验证修正渗透系数后的太沙基模型.图 5为拟合结果图,表 2为拟合参数值及利用参数值计算所得的毛细渗透系数值.表 2中A、B为拟合试验数据结果,其中B表示最大毛细上升高度hc的拟合值;n为孔隙率;k为毛细渗透系数,其值等于孔隙率n与A的比值.
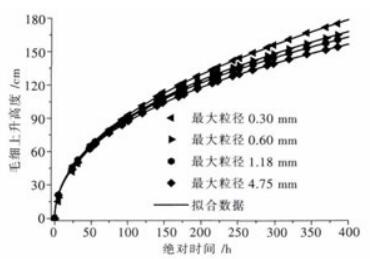 |
| 图 5 毛细上升高度与时间的拟合关系 Fig. 5 The fitting relation between capillary rise height and time |
| 表2 拟合结果及计算所得参数 Table 2 Fitting results and calculated parameters |
 |
| 点击放大 |
由图 5和表 2可以看出,利用修正后的太沙基模型,能较好地拟合离子型稀土毛细上升时上升高度与时间关系的试验数据,对4种不同粒径的稀土,其拟合的相关系数都在0.99以上.从拟合结果中可直接得到毛细渗透系数k,以此表达毛细渗透能力的大小.因此图 5和表 2的结果证明从试验事实出发,利用修正后的太沙基模型获取毛细渗透系数的方法简捷可行.
3.2 渗透系数的比较本文提出的太沙基修正模型的关键是得到可以直观表达毛细上升作用大小的渗透系数,重新定义其中的渗透系数,用毛细渗透系数k代替饱和渗透系数ks.为验证修正后的毛细渗透系数较饱和渗透系数贴近试验事实,分别用参数代入模型拟合试验数据.
比较太沙基模型和修正模型可以发现,2个模型表达形式一样,因此2个模型所预测的最大毛细上升高度值相同.将饱和渗透系数ks和最大毛细上升高度代入式(3)得到太沙基模型曲线,用毛细渗透系数k代替饱和渗透系数ks得到修正模型曲线,4组粒径对比曲线如图 6所示.由图 6可以看出,取定同一稀土的最大毛细上升高度,太沙基模型拟合曲线与试验数据偏差较大,而修正模型与试验数据吻合较好;当毛细上升高度为定值时,太沙基模型所需的时间较实际少.
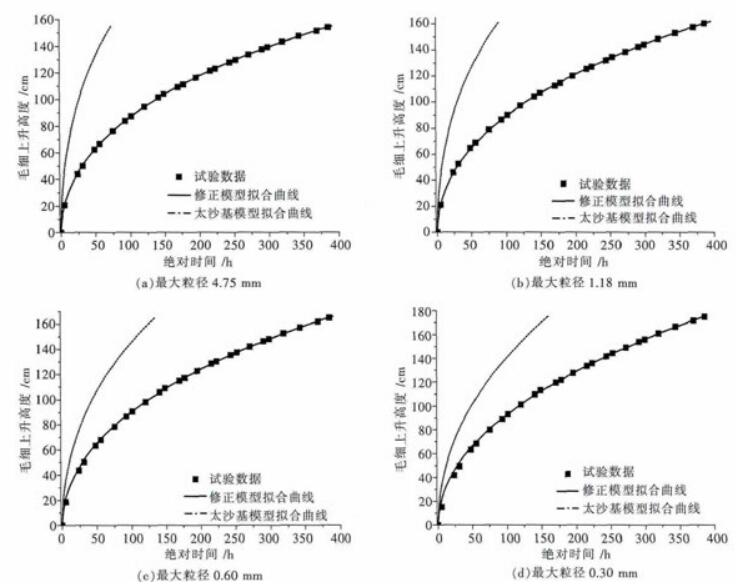 |
| 图 6 修正模型、太沙基模型曲线与实测数据的比较 Fig. 6 Comparison between curves of updated model, original model and test data |
对比结果表明,渗透系数的取值对模型是至关重要的.太沙基模型用入渗过程的饱和渗透系数定义毛细上升过程的渗透能力不但夸大了毛细上升过程速率的大小,而且理论结果与毛细上升高度之间的差值随着时间的推移不断增大.而毛细渗透系数根据实测的试验数据中得到,有效避免了理论结果与试验事实之间的差异.就渗透系数取值的数量级而言,在离子型稀土渗透系数的取值范围内,同时修正后的太沙基模型拟合数据与实测试验结果很好的吻合,相比饱和渗透系数,毛细渗透系数表现出的渗透能力稍弱,也从数值大小角度间接体现了非饱和土渗透力小于饱和土的渗透力.
4 毛细渗透系数的应用 4.1 毛细渗透系数和最大毛细上升高度的经验关系将毛细渗透系数代入式(6)和(7)表示的太沙基模型,拟合不同情况下毛细上升试验数据,可以得到毛细渗透系数k、最大毛细上升高度hc、达到最大毛细上升高度需要的时间以及毛细上升时的影响因素.离子型稀土矿土由花岗岩等经过风化得到的,里面包含有粒径较大、没有充分风化的矿物晶体,由试验结果可知大粒径晶体颗粒对毛细上升的影响明显. 图 7为土体粒径大小对毛细渗透系数和最大毛细上升高度的影响.由图 7可以看出,土体毛细渗透系数随着土体大颗粒的增多逐渐增大,二者呈指数关系,经验关系为k=0.051 8(1-e-2.608 8d),其中d为土体大颗粒晶体粒径,k为毛细渗透系数;最大毛细上升高度随土体粒径的增加而减小,二者呈幂函数关系,经验关系为hc=354.78+230 0×0.005 07d,其中d为土体大颗粒晶体粒径,hc为最大毛细上升高度.
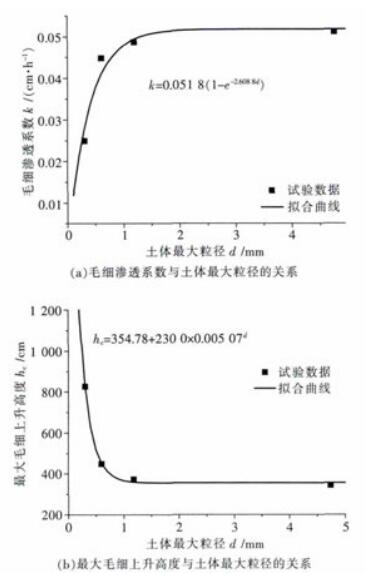 |
| 图 7 最大毛细上升高度、毛细渗透系数与土体最大粒径的关系 Fig. 7 The relations between maximum height of capillary rise, capillary permeability coefficient and maximum grain size of ionic rare earth |
造成上述现象的原因在于4组土样增加的大颗粒成分不同.不同粗颗粒的增加改变了毛细通道骨架结构,使毛细水能在颗粒空隙顺利推进,加快了上升过程;反之,随着土样的大粒径晶体的减小,细颗粒取代粗颗粒填充空隙,减小了毛细渗透通道,且细小空间的粉土遇水易形成水膜,使得原本变小的部分孔隙被结合水阻断,形成水分不流通的死角,从而导致毛细渗透系数的减小.
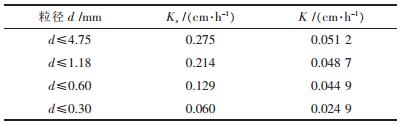
表 3为土样饱和渗透系数和毛细渗透系数值.由表 3可以看出,对同一土样,毛细渗透系数总小于饱和渗透系数.非饱和土毛细上升是一个非饱和非稳定的过程,渗透系数变化情况错综复杂,对其进行定量分析难度较大,毛细渗透系数不计瞬时渗透系数的变化规律,结合模型将非饱和毛细上升能力量化为毛细渗透系数,然后根据试验实测数据逆推毛细规律,这是本文的一个创新点.
| 表3 饱和渗透系数与毛细渗透系数对比 Table 3 Comparison between saturated permeability coefficient and capillary permeability coefficient |
 |
| 点击放大 |
4.2 毛细上升速率的确定
利用修正模型拟合试验数据得到的表 2所示A、B参数值,再结合式(7)表示的毛细上升率与上升高度的关系,可以得到毛细上升率与时间的拟合关系,如图 8所示.由图 8可以看出,利用修正的毛细渗透系数,可以较好地拟合(或预测)毛细上升速率随时间的变化规律,这为工程实际中测算不同时间毛细上升速率以及达到最大毛细上升高度提供了理论依据.
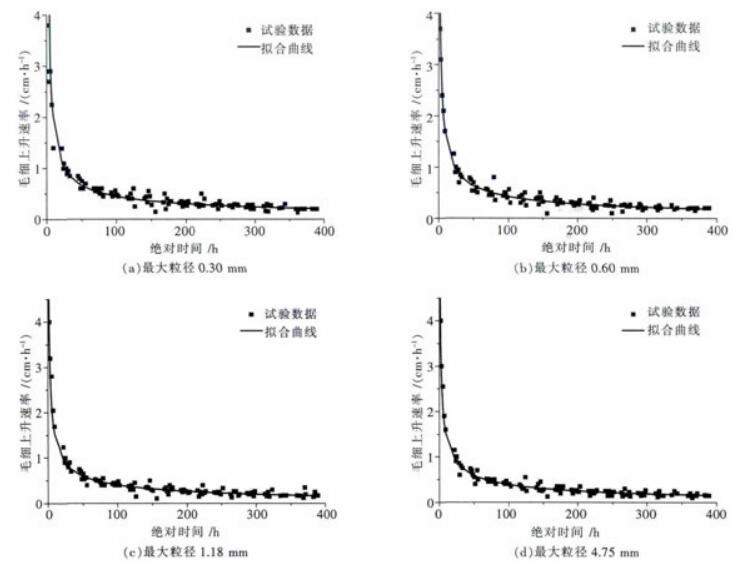 |
| 图 8 毛细上升速率与时间的拟合关系 Fig. 8 The Fitting relation between capillary rise velocity and time |
5 结论
1)针对太沙基毛细上升模型中饱和渗透系数与实际毛细上升情况不一致,定义毛细渗透系数k代替太沙基毛细上升模型中饱和渗透系数ks表示毛细上升能力,得到修正后的太沙基毛细上升模型,并用不同粒径的离子型稀土毛细上升试验进行验证,结果表明修正后的毛细渗透系数较饱和渗透系数更好减小了模型与试验事实之间的差异.
2)清水在离子型稀土中发生毛细上升时,毛细渗透k随土体大颗粒晶体的增加而减小,二者呈指数关系;最大毛细上升高度随土体大颗粒晶体的增加而增加,二者呈幂函数关系.
3)从试验事实出发,毛细渗透系数直观的量化了非饱和土毛细渗透能力.对粒径级配相同的稀土土样,毛细渗透系数小于饱和渗透系数.
4)应用修正后的毛细渗透系数,可以较好地拟合(或预测)毛细上升速率随时间的变化规律.毛细上升速率随时间呈现先快速下降、后缓慢减小的趋势.
| [1] | 田君, 唐学昆, 尹敬群, 等. 风化壳淋积型稀土矿浸取过程中基础理论研究现状[J]. 有色金属科学与工程, 2012, 3(4): 48–52. |
| [2] | 罗嗣海, 黄群群, 王观石, 等. 离子型稀土浸矿过程中渗透性变化规律的试验研究[J]. 有色金属科学与工程, 2014, 5(2): 95–99. |
| [3] | 吴爱祥, 尹升华, 李建锋. 离子型稀土矿原地溶浸溶浸液渗流规律的影响因素[J]. 中南大学学报(自然科学版), 2005, 36(3): 506–510. |
| [4] | 罗仙平, 翁存建, 徐晶, 等. 离子型稀土矿开发技术研究进展及发展方向[J]. 金属矿山, 2014(6): 83–90. |
| [5] | 汤洵忠, 李茂楠, 杨殿. 原地浸析采矿中的溶液毛细损失及其对策[J]. 湖南有色金属, 1999, 15(5): 6–10. |
| [6] | 张志军, 李亚俊, 刘玄钊, 等. 某金属矿山尾矿坝中毛细水的上升规律[J]. 中国有色金属学报, 2014, 24(5): 1345–1351. |
| [7] | 姜啸, 张虎元, 严耿升, 等. 湿度对盐溶液在壁画地仗中的毛细迁移影响研究[J]. 岩土力学, 2014, 35(2): 459–465. |
| [8] | 马志鸣, 赵铁军, 王鹏刚, 等. 矿物掺合料对混凝土毛细吸收作用影响的试验研究[J]. 混凝土, 2014(3): 87–89. |
| [9] | 陆文攀, 赵铁军, 马志鸣, 等. 荷载损伤对混凝土毛细吸收作用影响[J]. 硅酸盐通报, 2015(1): 50–54. |
| [10] | 谈云志, 孔令伟, 郭爱国, 等. 压实红黏土水分传输的毛细效应与数值模拟[J]. 岩土力学, 2010, 31(7): 2289–2294. |
| [11] | 赵明华, 刘小平, 陈安. 非饱和土路基毛细作用分析[J]. 公路交通科技, 2008, 25(8): 26–30. |
| [12] | 李顺群, 栾茂田, 杨庆. 考虑基质吸力变化时非饱和土的一维本构模型[J]. 岩土力学, 2006, 27(9): 1575–1578. |
| [13] | 何克瑾, 费良军, 尹娟. 均质土壤上升毛管水运动特性试验[J]. 沈阳农业大学学报, 2007, 38(4): 581–585. |
| [14] | 杜红普, 刘波, 王华军, 等. 基于土水特征曲线预测多孔介质毛细上升过程[J]. 工程地质学报, 2013, 21(3): 345–350. |
| [15] | 张昭, 刘奉银, 张国平, 等. 土在全含水率范围内持水及非饱和渗透特性的模型描述[J]. 岩石工程学报, 2014, 36(11): 2069–2077. |
| [16] | 韦昌富, 侯龙(译).非饱和土力学[M].北京:高等教育出版社, 2012. |
| [17] |
Lu N, Likos W J. Rate of capillary rise in soil[J].
Journal of Getechnical and Geoenvironmental Engineering, 2004, 130(6): 646–650. DOI: 10.1061/(ASCE)1090-0241(2004)130:6(646). |
 2015, Vol. 6
2015, Vol. 6

