| 基于Flu ent的电磁场中铝熔液及其微粒运动轨迹的数值模拟 |
b. 江西理工大学材料科学与工程学院,江西 赣州 341000
b. School of Material Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
在半固态合金浆料制备中,电磁搅拌[1]是最主要的手段,归因于其非接触式的搅拌方式[2],克服了机械搅拌污染金属浆料的不足,可获得更细小均匀的等轴晶,控制也灵活方便,也是迄今最成功的制备半固态铝合金坯料的方法.在半固态浆料的制备过程中,铝合金熔体处于固液两相共存现象,黏性较纯液体时更大;此外,实际生产和研究中的铝合金都是多元体系,而且为了进一步提高半固态铝合金浆料的质量,还需要在熔体中添加细化剂(如AlTiB、RE、Zr、Na)等.在黏稠的铝合金熔体中的合金元素、细化剂等物质能否实现设定的功效,与它们在合金熔体中的分布不无关系.以往的研究表明[3-5],在黏稠的熔体中,细化剂的扩散迁移将受到熔体流动特性的影响,易沿着熔体流线运动、扩散、迁移,最终依据熔体流线的轨迹[6]而分布.为此,需要控制细化剂在熔体中的传输、扩散、混合与分布,保证合金熔体的最终质量.在早期研究中,主要从宏观实验测量方法对其进行研究,但是电磁场中熔液内部流场的复杂性,沿用以前传统的办法难以了解其内部微观扩散情况.随着流体动力学的发展,CFD(Computational Fluid Dynamics)软件Fluent对其内部熔液流动情况进行数值模拟[7-17],并对其流场进行分析,也有助于更好深入认识电磁场中半固态铝合金熔液内部流场特性.在当前这方面的研究中,人们考虑更多的是熔体本身的流动状态(如自然对流或强制对流[18])对合金凝固组织形貌的影响,尚未进一步探究熔体流动特性(如层流流动或紊流流动[19])的影响与作用.因此,还需要研究铝合金中细化剂在熔体流动过程中的扩散路径、迁移轨迹与分布规律等.考虑到铝合金熔体在电磁场作用下流动的实际情况,本文是以湍流模型进行分析.在分析过程中,假定铝合金熔体中的细化剂可看成为无数个微小质点,并且将质点当作一个理想化模型,忽略其体积或形状,那么,通过调节不同磁场频率来研究铝合金熔体内部流场分布及微粒运动轨迹,最终实现细化剂在铝合金熔体中传输、扩散、分布的模拟.
1 模型建立 1.1 几何建模和网格划分为了便于研究,将盛装铝合金熔体的容器(坩埚)简画成圆柱体,借助pro/E软件简画出模型外形,如图 1所示.该模型坐标原点位于圆柱底面中心,半径为3 cm,高为12 cm,Gambit为Fluent软件前处理软件,其功能主要是进行模型网格划分及边界条件设定,是整个数值模拟的前提.
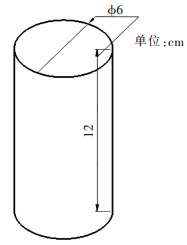 |
| 图 1 模型几何简图 Fig. 1 Geometric diagram of model |
Gambit中可以使模型进行线网格划分、面网格划分和体网格划分,鉴于此为三维模型,可采用四面体、六面体及楔形体相结合的体网格划分,得到模型网格总数为190 190个,并对其4个方向进行观察,如图 2所示.在指定边界条件类型中,Gambit中提供了22种流动进、出口条件,对于流体区域、黏性流动中壁面(Wall)界面通过指定剪切来模拟滑移壁面.根据所用模型,选择圆柱体3个面皆为Wall界面.
 |
| 图 2 模型网格划分 Fig. 2 Mesh generation of model |
1.2 模型计算
众所周知,流体的运动一般要遵循3个基本守恒原则:质量守恒定律、动量守恒定律、能量守恒定律.当铝合金熔体在电磁搅拌器受到Lorentz力搅拌时,铝合金熔体受电磁力的搅拌而发生运动.假设熔体流动是不可压缩流动,且在电磁搅拌器内为非定常流动.所以,不可压缩流体连续性方程为:
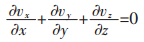
|
(1) |
速度vx,vy,vz沿各自坐标轴的变化相互约束,不可压缩流体在流动过程中虽有变化但是体积不变.
当质点做有规则的运动,且质点之间运动互不干扰、互不混杂,则为层流(稳流)运动;反之,质点运动混乱、无规则则为湍流运动.一般以雷诺数[20]Re为判断标准,当Re > 2 300时,质点则为湍流运动,公式为:
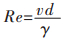
|
(2) |
式(2)中,v表示质点运动速度,d表示容器形状的当量直径,γ表示熔体的动力黏度.并可以看出Re与质点速度互相制约影响,当质点速度增大时,Re也随着增加.已知A356铝熔液的动力黏度[21]为1.2×10-5 kg/m;根据电磁场每分钟转速n=60f/p,可获知模拟选用最小频率5 Hz时,转速为1 m/s;容器的当量直径根据所画模型(如图 1所示),d为6 cm,根据所给数据得出Re=5×105,远远大于2 300,所以选择湍流模型.
标准的k-ε湍流模型适用范围广,计算量合适,有相当的精确度和数据积累,是个半经验公式.其湍流能公式为:
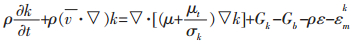
|
(3) |
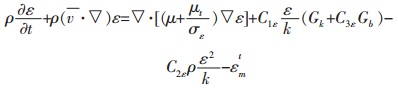
|
(4) |
式(1)、式(2)和式(3)中,Gk表示速度梯度引起的湍动能;Gb表示浮力引起的湍动能;C1ε,C2ε和C3ε是常数;σk和σε分别是k方程和ε方程的Prandtl数;μτ为湍流黏性系数.
研究电磁场中流体运动,首先运用电磁方程理论,J C麦克斯韦总结出的电磁场运动数学表达式,其Maxwell方程组为:
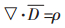
|
(5) |
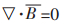
|
(6) |
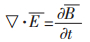
|
(7) |
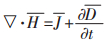
|
(8) |
式(4)、式(5)、式(6)和式(7)中,D、ρ、B、E、H和J和分别表示电位移矢量、电荷密度、磁感应强度、电场强度、磁场强度和电流密度.
采用MHD模块导入磁场,Kitamura[22]给出MHD流体的k-ε方程源项:
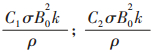
|
其中相应的经验常数分别为C1=1.44和C2=1.92.
采用MHD源项对k-ε湍流方程进行修正,使其能充分湍流流动的影响,对于不可压缩流体充分考虑其表面情况应用条件,更加合理地模拟流体在电磁场中流动.
1.3 边界条件与计算方法所研究的电磁场内的流体为A356铝熔液,其液态密度为2 630 kg/m3,动力黏度为1.2×10-5 kg/m,热导系数为161W/m,比热为880 J/kg;而该合金的液相线温度与固相线温度分别为615.6℃(888.6 K)和576.1℃(849.1K),其物理性能由PROCAST软件材料数据库和文献[23-24]获得.电磁场为交流场,其频率分别为5 Hz、10 Hz和20 Hz,根据电磁场每分钟转速n=60f/p(f为磁场频率;p为磁极数,实验所用为3极),所对应的流体初始搅拌速度为1.0 m/s、2.0 m/s和4.0 m/s;电磁场搅拌时间均为15 s(即步长为150);压力为一个标准大气压;初始温度为923 K(即650 ℃).选用MHD磁场模块和标准k-ε湍流模型.动量方程、湍动能方程和湍动能耗散率均采用一阶迎风差分格式,采用SIMPLE算法求解温度与质点粒子轨迹.
2 计算结果与分析 2.1 温度场分析根据所建立的模型,模拟计算了不同电磁场频率作用下搅拌终了时铝合金熔体中的温度场分布情况,结果如图 3、图 4和图 5所示.
 |
| 图 3 磁场频率为5 Hz时铝合金熔体内部的温度场 Fig. 3 Temperature field in aluminum alloy at electromagnetic frequency 5 Hz |
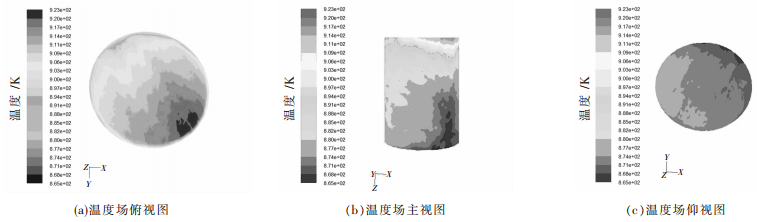 |
| 图 4 磁场频率为10 Hz时铝合金熔体内部的温度场 Fig. 4 Temperature field in aluminum alloy at electromagnetic frequency 10 Hz |
 |
| 图 5 磁场频率为20 Hz时铝合金熔体内部的温度场 Fig. 5 Temperature field in aluminum alloy at electromagnetic frequency 20 Hz |
从模拟结果中可以看出,当搅拌频率为5 Hz时,只有表面少部分熔体的温度处于浇注温度923 K(见图 3(a)所示),且温度降低幅度大,熔液内部大部分的温度都比浇注温度低(见图 3(b)所示),而且位于坩埚底部的铝合金熔体的温度大致在860 K左右(见图 3(c)所示),已进入固液两相区.当搅拌频率为10 Hz时,大部分处于坩埚表面的熔体温度均在900 K左右,且均匀分布,只有处于边缘部位极少熔体的温度接近于浇注温度(见图 4(a)所示),而处于坩埚内部的熔体温度比坩埚表面的熔体温度降低快(见图 4(b)所示),处于坩埚底部的少部分熔体的温度在860 K左右,此温度恰好处于A356合金液相线温度与固相线温度之间,正在凝固的液相或包裹着游离的固相颗粒,或与从铸型壁生长出的固相接触,形成凝固界面前沿,使得该区域的熔体处于固液相共存状态.当搅拌频率为20 Hz时,由于搅拌频率较高且搅拌功率较大,处于坩埚表面的熔体温度分布较均匀约为910 K(见图 5(a)所示),靠近坩埚壁的熔体温度比坩埚中部的熔体温度高(见图 5(b)所示),而位于坩埚底部的熔体比坩埚表面和坩埚内部的熔体温度降低快且分布均匀(见图 5(c)所示).首先,由于温度最高点靠近熔液表面一侧,通入磁场时,绕组及定子产生的热量大部分由定子传给搅拌器机壳,机壳表面对流散热传递给流体介质,且速度越大热量传递越多,大部分热量由熔液表面散失到空气中.其次,磁场对熔液有一定搅拌作用,可以对熔液起加热作用.但在空气中高温熔体遇冷迅速降低温度,所以离坩埚表面越远,降温速度越快.从低频率增加到高频率时,熔体表面温度明显成梯度变化,熔体内部温度减少趋势减弱,中部温度低,端部温度高.随着频率升高,温度差趋之增.即频率越大,磁场转动速度越快,流体产生能量越大,导致熔体内部端部温度越高,且温度差也随之增大.同时,频率越大,电磁场会导致熔液三维空间上的温度场均匀化.
2.2 熔体内细化剂微粒运动轨迹选取初始坐标(0,0.5,4)、(1,1,10)和(2,1,6)绘制细化剂微粒运动轨迹,细化剂微粒为单独质点,其轨迹模拟状态为A356铝合金熔融状态,步长均为150步.将轨迹数据导入Matlab软件中,可以直观的显示微粒在电磁场内运动轨迹.图 6、图 7和图 8为不同频率下细化剂微粒运动轨迹.
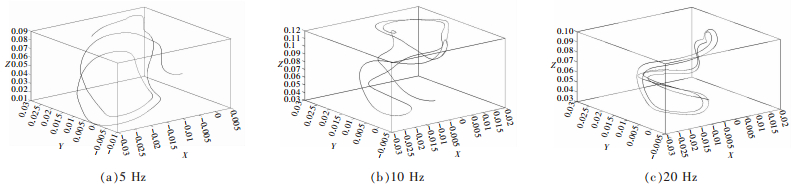 |
| 图 6 不同频率下坐标(0,0.5,4)的细化剂微粒运动轨迹 Fig. 6 Particle trajectories of refiner in coordinate (0, 0.5, 4) at the different frequencies |
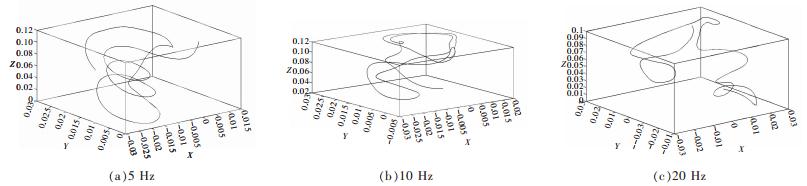 |
| 图 7 不同频率下坐标(1,1,10)的细化剂微粒运动轨迹 Fig. 7 Particle trajectories of refiner in coordinate (1, 1, 10) at the different frequencies |
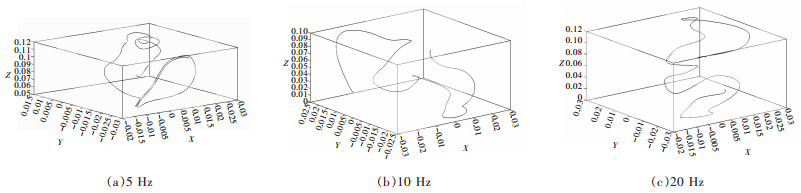 |
| 图 8 不同频率下坐标(2,1,6)的细化剂微粒运动轨迹 Fig. 8 Particle trajectories of refiner in coordinate (2, 1, 6) at the different frequencies |
磁场转动时,熔体每一处都产生感应电动势,感应电动势使熔体产生感应电流,感应电流与磁场作用使熔体受Lorentz力作用,Lorentz力在径向、切向和轴向的分量使熔体在竖直面和水平面内剧烈运动,熔体内微粒在磁场产生复杂三维流动.从图 6、图 7、图 8中可以明显看出,点(0,0.5,4)分别在5 Hz时,运动流线为较规律的转动状态(见图 6(a)所示);在10 Hz时,运动流线已不规则的湍动(见图 6(b)所示);在20 Hz时,微粒运动流线受强磁场扰动,湍动剧烈(见图 6(c)所示).点(1,1,10)和点(2,1,6)分别在5 Hz、10 Hz和20 Hz时,微粒运动流线规律也同点(0,0.5,4)类似(见图 7、图 8所示).在同频率时,如在20 Hz下,点(0,0.5,4)运动流线比点(1,1,10)和点(2,1,6)湍动更为显著(见图 6(c)所示),远离中心轴即靠近坩埚壁的质点运动轨迹较为平缓.当频率为5 Hz和10 Hz时,微粒运动流线也有此规律.即当位置相同,搅拌频率不同时,微粒运动带有很大的随机性,都为呈非线性运动.即便是初始位置一样,但最终位置也不一样.随着频率增加,熔体细化剂微粒运动轨迹更加复杂,运动幅度变大,受磁场湍动更显著.频率越大,导致电磁搅拌过程中熔体内的两相之间的相互碰撞越剧烈,同时电磁搅拌给液相提供了更多能量,轨迹比低频率时复杂.当位置不同,搅拌频率相同时,微粒依然呈非线性运动,越靠近中心坐标轴的位置,熔体细化剂微粒运动轨迹受湍动更显著,其轨迹较远离中心位置质点的复杂.熔液作为导体,外加上磁场的作用引起熔体中心形成涡流电流,越靠近中心,电流作用越强,微粒运动越频繁,导致位置越靠近中心微粒的轨迹越复杂.
3 结论1)采用Fluent软件中的MHD模块和标准k-ε模型,对磁场内熔体进行数值模拟,能较好的模拟熔体内的温度变化及熔体中细化剂微粒的运动轨迹,也为今后研究铝合金熔体在电磁场作用下的混沌对流奠定了基础.
2)在不同电磁场搅拌频率作用下,通过对铝合金熔体温度场及细化剂微粒运动轨迹的模拟与分析,可知:随着电磁场频率增大,电磁场旋转速度越快,产生的搅拌力和能量越大,熔体整体温差小,温度趋于均匀化;随着频率增加,微粒运动轨迹越复杂,受磁场扰动越显著;越靠近中心坐标位置的细化剂微粒的运动轨迹越复杂.
3)仅对铝合金熔体在电磁场作用下其温度分布与微粒运动进行了数值模拟,在以后研究中还要运用熵、Lyapunov指数和分形维数对其进行计算,判断其是否发生混沌对流,并对电磁搅拌参数进行优化,以对混沌现象作进一步深入研究.
| [1] |
Griffiths W D, McMartney D G. The effect of electromagnetic stirring during solidification on the structure of Al-Si alloys[J].
Materials Science and Engineering A, 1996, 216(1/2): 47–60. |
| [2] | 白云峰, 周月明, 严彪, 等. 电磁场在材料凝固加工领域的应用[J]. 铸造, 2008, 57(2): 105–109. |
| [3] |
Liu Z H, Zeng Q Q. Study on laminar mixing enhanced by flexible impeller in high-viscosity fluid stirred tank[J].
China Science Paper, 2012, 7(3): 185–189. |
| [4] |
Timmel K, Eckert S, Gerbeth G. Experimental investigation of the flow in a continuous-casting mold under the influence of a transverse, direct current magnetic field[J].
Metallurgical and Materials Transactions, 2011, 42B: 68–80. |
| [5] |
Haghayeghi R, Ezzatneshan E, Bahai H, et al. Numerical and experimental investigation of the grain refinement of liquid metals through cavitation processing[J].
Metals and Materials International, 2013, 19(5): 959–967. DOI: 10.1007/s12540-013-5008-0. |
| [6] | 刘作华, 孙瑞祥. 刚-柔组合搅拌浆强化流体混沌混合[J]. 化工学报, 2014, 9(65): 3340–3349. |
| [7] | 赵秀艳.金属射流的MHD特性分析[D].济南:山东农业大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10434-2009234414.htm |
| [8] | 杨锦凌, 孙大鹏. 基于FLUENT二次开发的数值波浪水槽[J]. 中国水运, 2012, 5(12): 59–61. |
| [9] | 李荣, 冯永保. 基于Fluent的电磁阀内部流场的三维仿真与分析[J]. 液压与气动, 2013, 10(25): 96–98. |
| [10] | 王福军. 计算流体动力学[M]. 北京: 清华大学出版社 , 2004. |
| [11] | 邱立杰, 张国福. 基于FLUENT的弯管内部流场的数值模拟[J]. 辽宁石油化工大学学报, 2013, 33(1): 48–52. |
| [12] |
Prasanta K S, Mullick A N. Computational investigation of performance characteristics in a C-shape diffusing duct[J].
International Journal of Advances in Engineering & Technology, 2013, 3(1): 129–136. |
| [13] |
Yang W, Wang Y, Chen J. Computation fluid dynamic simulation of fluid flow in a rotating packed bed[J].
Chemical Engineering Journal, 2010, 156: 582–587. DOI: 10.1016/j.cej.2009.04.013. |
| [14] |
Lamberto D J, Alvarez M M. Computation analysis of regular and chaotic mixing in a stirred tank reactor[J].
Chemical Engineering Science, 2001, 56(16): 4887–4899. DOI: 10.1016/S0009-2509(00)00407-3. |
| [15] |
Ranade V V, Rampure M. Hydrodynamic of bubble column reactors at high gas velocity: Experiments and computational fluid dynamics (CFD) simulations[J].
Industrial & Engineering Chemistry Research, 2007, 46(25): 8431–8447. |
| [16] |
Zale J M, Szalai E S. Using CFD to understand chaotic mixing in laminar stirred tanks[J].
Aiche Journal, 2002, 48(10): 2124–2134. DOI: 10.1002/(ISSN)1547-5905. |
| [17] | 石玉峰, 许庆彦, 柳百成. 对流作用下枝晶形貌演化的数值模拟和实验研究[J]. 物理学报, 2011, 60(12): 376–386. |
| [18] |
Ritwik R, Prasada Rao A K, Dhindaw B K. Low-convection-cooling slope cast AlSi7Mg alloy: A rheological perspective[J].
Journal of Materials Engineering and Performance, 2013, 22(9): 2487–2492. DOI: 10.1007/s11665-013-0530-2. |
| [19] |
Liu Z, Hu Y M, Liu X M. Research on refining mechanism of yttrium on primary α-Al in semi-solid Al alloy[J].
Acta Metallurgica Sinica (English Letters), 2010(4): 277–284. |
| [20] | 杜诚实, 徐敏义, 米建春. 雷诺数对圆形渐缩喷嘴湍流射流的影响[J]. 物理学报, 2010, 59(9): 6331–6338. |
| [21] | 曾珊琪, 程大勇, 郭敏杰. 基于ADINA的A356铝合金压铸模成型数值模拟分析[J]. 热加工工艺, 2011, 12(23): 54–58. |
| [22] |
Kitamura K, Hirata M. Turbulent heat and momentum transfer for electrically conduction fluid flowing in two dimensional channel under transverse magnetic field[J].
Proceedings of the 6th International Heat Transfer Conference, 1978, 3(8): 159–164. |
| [23] | 路贵民, 赵大志, 王平, 等. A356铝合金半固态成形的数值模拟[J]. 东北大学学报, 2007, 28(3): 353–356. |
| [24] | 陶文毓, 赵升吨, 林文捷. A356铝合金半固态浆料电磁搅拌法制备过程的数值模拟[J]. 机械工程学报, 2012, 48(14): 50–57. |
 2015, Vol. 6
2015, Vol. 6

