| 生产爆破下巷道顶板稳定性的动态应力比分析评价 |
地下矿山巷道顶板的稳定性,关乎着生产活动能否安全有效地进行[1-6].由于我国金属矿山主要采用钻孔爆破法进行开采,若采场附近存在巷道,则生产爆破过程易对巷道围岩,尤其是顶板围岩产生扰动和损伤,甚至引起围岩失稳破坏[7-12].通常对于巷道顶板的稳定性研究是以国家爆破安全标准为判断依据,利用萨道夫斯基公式对最大单段药量或总药量进行控制.但是由于萨道夫斯基公式无法反映多段微差爆破时的振动强度,而且国家标准关于矿山巷道的安全振速并未对不同地质条件、不同支护条件等实际问题做出规定,这使国家标准在用于指导客观生产实践时略显宽泛.由于地下采场中顶板稳定性问题最为复杂,国内外对其进行了大量研究并取得了一定成果.周科平[13]利用灰色系统理论预测采场顶板稳定性及其沉降规律;杨双锁等[14]利用有限元法对采场顶板稳定性进行定量分析及分类研究;张树光等[15]应用离散元法对顶板稳定性进行分析;曹文贵等[16]对潭邵高速公路路基岩溶顶板稳定性二级模糊进行了综合评判.近年来随着计算机技术的发展,数值分析方法逐渐应用于该领域的研究,但由于数值计算和模拟难以真正反应爆破振动下采场顶板的变化,更不能准确地确定采场顶板损伤破坏的位置,该方法对指导工程实践有一定的局限性.
为了明确临近巷道生产爆破对巷道顶板产生的实际影响,以某矿为例,对巷道顶板进行实际爆破振动测试,并在分析振动峰值与振动主频的基础上,结合动态应力比评价体系对巷道顶板的稳定性做出安全评价.
1 工程概况某地下铁矿矿区位于龙岩盆地东南边缘,其东界为天山凹断层,西界为溪马河断层,东西长约4 000 m,南北宽700~1 000 m.矿区介于分水岭至河谷地带,地势由东向西逐渐降低,地形高程420~892 m,两侧山坡较陡,天然坡度为15°~35°.矿体主要集中于550~750 m高程范围内.勘查中将矿区划为东、中、西3个矿段,本次讨论范围是标高为420~200 m的中西矿段.该矿区主矿体主要为磁铁矿,围岩主要为石英岩.
该矿床采用无底柱崩落法开采.矿体采用后退式开采,且自上而下进行;同分段,上盘超前回采,相邻矿块超前回采时,一般不超过1~2个分段;上下分段同时回采时,上分段超前下分段25~30 m距离.落矿采用垂直扇形中深孔爆破.炮孔直径75~80 mm;炮孔向前倾斜8°~10°,边孔水平夹角55°~60°;每排9孔,炮孔排距2 m,孔底距2.1~2.4 m,最大孔深约25 m;炸药采用硝铵炸药;起爆采用导爆管、非电毫秒雷管、导爆索复式起爆.
2 爆破振动测试及分析随着回采工作的进行,回采中形成了巷道,由于矿体围岩较为完整稳固,开采过程中对部分巷道未进行处理.现阶段,随着开采的深入,中西矿段巷道稳定性问题日益凸显,巷道顶板是否稳定直接影响着该矿区开采活动是否能安全有序的进行.为了解该采区生产爆破对巷道顶板的影响,对代表性生产药量起爆时巷道顶板的爆破振动进行了测试.测试仪器为产自加拿大的Blastmate Ⅲ型测震仪.该仪器测量范围为:振速254 mm/s;噪声88~148 db;频响2~300 Hz.测试所得各点爆破振动曲线见图 1.
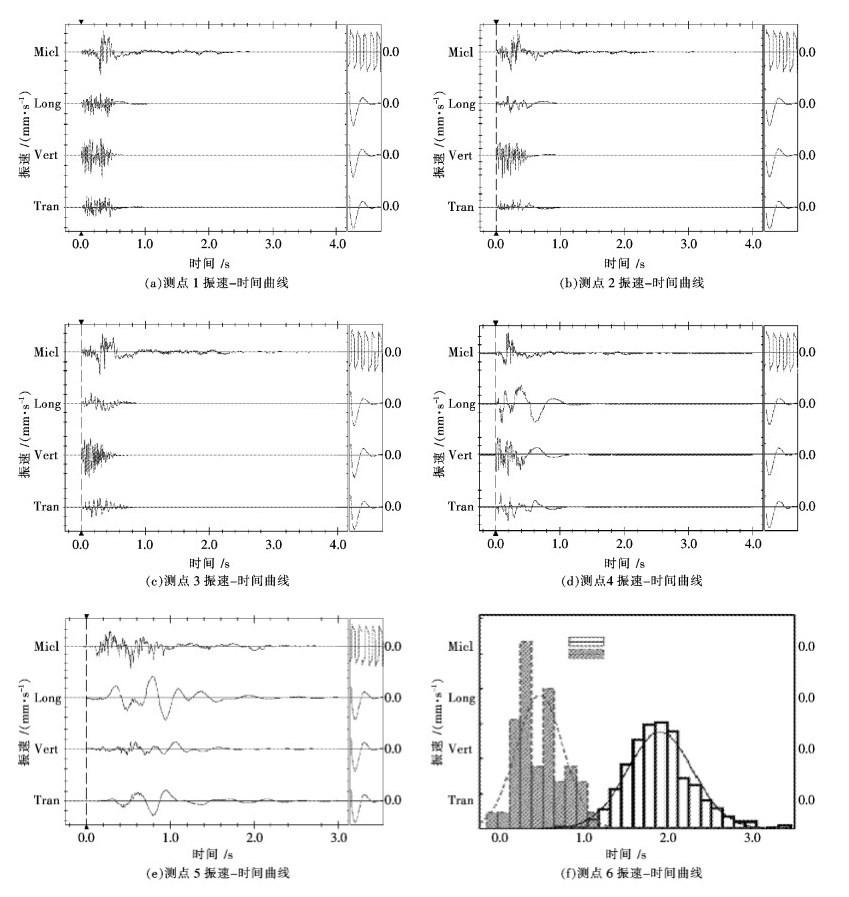 |
| (注:图 1中Micl表示空气冲击波强度,Long表示爆破地震水平径向振动,Vert表示表示爆破地震垂直方向振动,Tran表示爆破地震水平切向振动;对空气冲击波强度在此不予以研究讨论.) 图 1 各测点爆破振动曲线 Fig. 1 Velocity curves of different points |
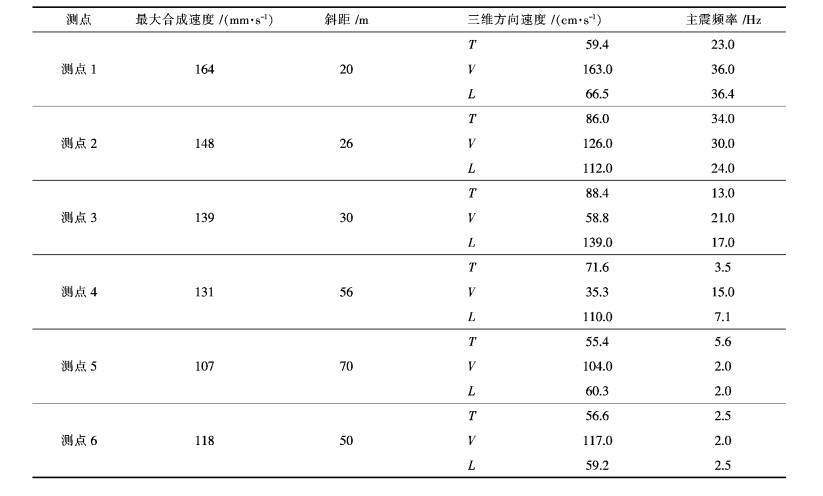
分析图 1可得,测点6振动时间较长约为2.5 s,测点5爆破振动持续约2 s,其余测点爆破振动持续时间均略小于1 s;可知该矿山在日常生产中产生的爆破振动持续时间较短,均在3 s内.比较图 1中各点振动曲线可直观发现,图 1(a)、图 1(b)爆破振动曲线最为密集,图 1(c)次之,图 1(d)第3,图 1(e)、(f)最为稀疏.结合各测点距爆源的实际距离分析可知,随着测点到爆源距离的增加,爆破振动曲线整体上变得越来越稀疏,振幅越来越小,即爆破振动频率越来越低,爆破振动强度越来越弱.为了验证爆破振动主振频率随爆源距的变化关系,对爆破振动曲线进行傅立叶变换,以确定各测点爆破振动主振频率及各方向振速峰值;为便于观察对比,将各测点振速峰值及主振频率进行提取并以表格形式列出,见表 1.由表 1可明显得出随着测点到爆源距离的增加,振幅越来越小,即爆破振动频率越来越低,爆破振动强度越来越弱,验证了爆破振动曲线所反映结论的正确性.
| 表1 各测点振速峰值及主振频率 Table 1 The peak vibration velocity of monitoring points |
 |
| 点击放大 |
3 地下结构动态应力比评价分析
由于巷道的失稳破坏与岩性、支护、水环境等因素有密切关系,而国家爆破安全标准对地下构(建)筑物做出的判据较为宽泛,未对不同条件进行明确的规定,只是使用频率与振速峰值作为宽泛的评价标准,对指导工程实践有一定的局限性[17].为了能够较为全面的反映巷道受爆破振动时的动态应力状态和损伤破坏程度,可采用动态应力比评价体系作为国家爆破安全标准的补充对巷道顶板的损伤破坏进行分析[18].
动态应力比评价标准[19](见表 2),是一种综合了爆破振动水平、岩体特征性质、现场条件及岩土支护系统等因素的评价方法,其实质是通过对比分析围岩对爆破振动的动态与岩体结构(包括支护结构)本身抵抗爆破振动损伤破坏的能力,来确定岩土设施物遭受爆破振动时的损伤破坏判据.由于该体系结合了影响地下构(建)筑物失稳破坏众多影响因素,如振动强度、场地质量系数、岩体性质与支护方式等,故其能够比较全面地反映爆破震动下巷道顶板的损伤破坏情况.
| 表2 地下结构损伤、破坏判据 Table 2 Criterion about damage and failure of underground structure |
 |
| 点击放大 |
动态应力比评价体系中,利用DSR来反应地下构(建)筑物失稳破坏类型和程度,为无量纲参数,可按式(1)求得:
| $ DSR = \frac{\sigma }{{{k_s}{\sigma _\tau }}} $ | (1) |
式(1)中,σ表示爆破振动在岩体内传播产生的动态应力,单位为Pa;ks表示场地质量系数,ks≈PQD < 1;στ为岩体动态抗拉强度,单位为MPa.
由于爆破振动在岩体内传播产生的动态应力在实际生产过程中较难测试,经研究发现其可按式(2)计算:
| $ \sigma = d{c_0}v $ | (2) |
式(2)中,d为岩体密度,单位为kg/m3;c0为岩体纵波速,单位为m/s;v为爆破振动速度,单位为cm/s.
由式(1)与式(2)可得DSR计算式:
| $ DSR = \frac{{d{c_0}v}}{{{k_s}{\sigma _\tau }}} \times {10^{-8}} $ | (3) |
通过查阅该矿山水文地质资料及矿山前期研究资料可知,该采场围岩主要为石英岩,平均密度为2 640 kg/m3,极限抗压强度为2.2×107 Pa,纵波速c0为3 000~4 000 m/s,ks≈PQD=0.94.由式(3)可知:DSR正比于爆破振动速度v,为了尽可能保证开采活动的安全,计算中纵波速c0取均值,即3 500 m/s,振速取最大监测速度0.164 m/s作为计算速度进行分析.
将各参数代入式(3)计算可得:DSR=0.073,与表 2对比分析可知DSR≤0.125,说明巷道顶板无损伤破坏.即目前该采场以相同生产条件进行爆破生产时,该巷道顶板稳定,不会影响正常开采活动.
4 结论1)通过分析现场爆破振动测试结果,得到了随着测点到爆源距离的增加,振幅越来越小,即爆破振动频率越来越低,爆破振动强度越来越弱的结论;
2)在爆破测振的基础上,利用动态应力比评价标准对生产爆破时临近巷道顶板的稳定性进行了计算分析,结果可知,DSR≤0.125,以相同条件进行爆破生产时,所研究巷道顶板无损伤破坏.
分析可知,动态应力比评价体系中未对爆破振动主振频率及爆破振动持续时间,对地下建(构)筑的稳定性影响进行分析讨论,后续研究将进行深入讨论分析.
| [1] | GB6722-2003.爆破安全规程[S]. |
| [2] | 易长平, 卢文波, 张建华. 爆破振动作用下的地下硐室临界振速的研究[J]. 爆破, 2005, 22(4): 4–7. |
| [3] | 胡建华, 雷涛, 周科平, 等. 充填采矿环境下爆破振动效应预测与控制[J]. 爆破, 2009, 26(4): 81–84. |
| [4] | 汪茂华, 成涌. 铜绿山高分段中深孔充填采矿方法的爆破工艺技术[J]. 采矿技术, 2010, 10(2): 81–83. |
| [5] | 周训兵, 李仕雄, 平健. 矿山顶板安全预警新体系研究[J]. 金属矿山, 2010(12): 140–143. |
| [6] | 王成, 孙宝生, 张建, 等. 中国矿山安全现状与对策[J]. 矿业研究与开发, 2006, 26(2): 81–85. |
| [7] | 肖福坤, 孙豁然, 柳小波, 等. 爆破震动对巷道稳定性影响的模拟分析[J]. 矿业研究与开发, 2004, 24(5): 73–76. |
| [8] | 曹野, 陈宏伟. 基于时能密度的围岩爆破安全判据实验[J]. 解放军理工大学学报(自然科学版), 2013(3): 264–269. |
| [9] | 闫长斌.爆破作用下岩体累积损伤效应及其稳定性研究[D].长沙:中南大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10533-2007198139.htm |
| [10] | 周建雄.爆破地震作用下出矿围岩稳定性分析及控制技术研究[D].长沙:中南大学, 2013. |
| [11] | 陈清运, 蔡嗣经, 明世祥, 等. 采矿动压对采场巷道稳定性影响的研究[J]. 金属矿山, 2004(8): 16–19. |
| [12] | 刘炜, 宋卫东, 赵炳祁, 等. 爆破震动对巷道稳定性影响研究[J]. 金属矿山, 2011(1): 28–30. |
| [13] | 周科平. 采场顶板稳定性分析及其沉降规律的灰色预测[J]. 矿业研究与开发, 1994, 14(4): 44–49. |
| [14] | 杨双锁, 靳钟铭. 采场顶板稳定性进行定量分析及分类研究[J]. 山西矿业学院学报, 1997, 15(1): 27–31. |
| [15] | 张树光, 张向东. 离散元法在顶板稳定性分析中的应用[J]. 煤, 2000, 9(4): 15–16. |
| [16] | 曹文贵, 程哗, 袁腾芳, 等. 潭邵高速公路路基岩溶顶板稳定性二级模糊综合评判[J]. 公路, 2003(1): 13–16. |
| [17] | 宋光明, 江文明, 史秀志, 等. 岩土结构爆破地震动态应力比评价标准的研究[J]. 矿冶工程, 2000, 20(1): 23–25. |
| [18] | 王礼先. 水土保持工程学[M]. 北京: 中国林业出版社 , 2000: 55-67. |
| [19] | 史秀志, 杨月平, 程爱宝. 地下结构顶板爆破振动的动态应力比评价研究[J]. 矿业研究与开发, 2005, 25(2): 76–82. |
 2016, Vol. 6
2016, Vol. 6

