| 挤压工艺参数对挤压过程影响规律的仿真模拟研究 |
我国拥有极其丰富的铝矿资源,铝合金型材已被各领域广泛应用.铝合金型材生产过程中最主导技术以及关键的核心环节是挤压成型[1],型材质量的好坏决定于模具设计结构与挤压工艺参数,如何选择好的挤压工艺参数和延长挤压模具的寿命已成为各行业亟待解决的问题.型材挤压工艺参数设计是挤压设计中最为关键的要领之一,它主要包括挤压比、挤压速度、挤压温度等要素.挤压工艺参数设计合理与否直接关系到后续型材产品的表面质量以及挤压力大小,以往在对挤压工艺参数的选择上往往是通过反复试用以及经验获得,本文主要是通过对型材挤压过程进行仿真模拟,在试模挤压前利用仿真模拟技术对挤压加工进行模拟,通过改变挤压工艺参数的数值,计算获得实验现场无法获得的型材物理性能.
针对挤压过程的仿真模拟国内外做过类似的研究[2-5],本次研究就是以某6063空心铝型材挤压加工为研究为对象,以Altair Hyperxtrude软件为仿真模拟载体,基于Taguchi分析方法,获得挤压该型材时的最佳工艺参数配比,为企业生产提供参考,从而提高生产效率.
1 实验研究方法 1.1 Altair Hyperxtrude挤压仿真模拟软件的简介铝型材挤压成型在铝型材加工领域是一个高压高温以及复杂的非线性、大变形的热-力耦合的塑性成型加工过程,Altair Hyperxtrude是目前全球唯一专业的铝型材挤压仿真模拟软件,同时可以对模具结构进行优化的软件,可以进行正向挤压和反向挤压分析,求解类型有瞬态和稳态2种,hyerxtrude采用了ALE算法,ALE算法是以非线性的纳维叶-斯托克斯方程作为控制方程,有连续性、动量守恒和能量守恒3个基本方程控制[6-9].
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + {c_i}\frac{{\partial \rho }}{{\partial {x_i}}} + \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} = 0 $ | (1) |
动量守恒方程:
| $ \rho \left( {\frac{{\partial {v_i}}}{{\partial t}} + {c_i}\frac{{\partial {v_i}}}{{\partial {x_i}}}} \right) = \frac{{\partial {\tau _{ji}}}}{{\partial {x_i}}} + {p_i} $ | (2) |
能量守恒方程:
| $ \rho \left( {\frac{{\partial E}}{{\partial t}} + {c_i}\frac{{\partial E}}{{\partial {x_i}}}} \right) = \frac{{\partial {T_{ji}}{v_j}}}{{\partial {x_i}}} + {p_j}{v_j} + \frac{{\partial \left( {{K_{ij}}, {T_j}} \right)}}{{\partial {x_i}}} + {K_0} $ | (3) |
式(1)~式(3)中:v为材料的位移;ρ为材料密度;τ为柯西应力;T为热力学温度;E为内能;Kij为热传导系数;K0为单位体积的热源;t为时间;pi为作用于物体上单位质量的体力;ci为物质点相对于网格点的运动速度,即为对流速度.
1.2 Taguchi试验研究方法简介Taguchi试验设计主要的理论基础是概率论和数理统计,通过Taguchi设计理念可以减少试验次数,通过试验方案对比寻找最佳的工艺参数配比,从而降低成本、提高实际生产效率并获得表面质量和性能最佳的型材产品.Taguchi方法[10-12]利用正交表来选择试验条件和安排试验方案,它的最大优点就是利用最少的试验次数获得最佳的工艺参数,该设计方法是一种简单有效的方法,凭借其设计优点被广泛应用于工程、化工、加工等领域.如图 1所示描述了Taguchi试验设计的一般流程.
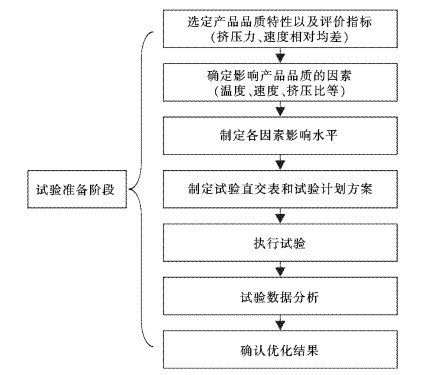 |
| 图 1 Taguchi试验流程 Fig. 1 Experiment process of Taguchi |
信噪比(S/N ratio)作为衡量质量特性的重要依据,用于系统和产品开发.本次研究采用信噪比(S/N ratio)来衡量5个挤压工艺参数对型材截面速度均方差、挤压力的影响规律以及对产品品质特性的影响规律,研究采用静态特性中的望小特性(smaller the better).为了更好地研究采用望小特性(smaller the better),对于望小质量特性服从Y~N(μ,σ2)分布,可将信噪比定义为S/N用η表示,即η=μ2/σ2,用信噪比来衡量产品特性的稳定性.为了使η更加接近于正态分布,使效应趋于线性可加性,将η值变成分贝(dB)值,即
| $ {\eta _{\rm{s}}} = 10{\rm{lg}}\eta $ |
望小特性希望Y越小越好,即可以认为μ2、σ2越小越好,所以可以将η的值变为
| $ \eta = \frac{1}{{{\mu ^2} + {\sigma ^2}}} $ |
即:
另一种表述方式为:
| $ S/N = \eta = {\rm{ - }}10\lg \left( {\frac{{\rm{1}}}{N}\sum\limits_{i = {\rm{1}}}^N {X_{\rm{i}}^2} } \right) $ | (4) |
式(4)中,Xi:表示第i次试验的试验值;i:表示试验的序号;N表示试验总次数.
2 挤压模型本研究的对象是山东某厂生产的型号为Y8255铝合金型材,该型材截面较复杂,每处壁厚分布不均匀.由于型材截面复杂的分布,相应建立了挤压模具三维图,上模外径为510 mm,厚度为130 mm如图 2,在上模上设有分流孔、分流桥、模芯等,下模如图 3,设有模孔焊合深度为17 mm.
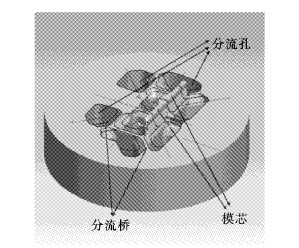 |
| 图 2 上模结构图 Fig. 2 Upper die structure |
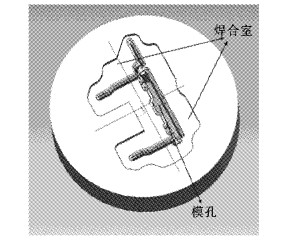 |
| 图 3 下模结构图 Fig. 3 Lower die structure |
将建立好的上模和下模进行组装,首先将组装好的三维模型图导入Hyperxtrude进行数值模拟,图 4为数值模拟分析模型,然后进行前处理,包括几何处理、网格划分等,在对网格划分时应注意以下3点:①型材最薄截面处至少划分6层单元网格;②对工作带区域划分时,沿挤压正方向至少划分9层单元网格;③自由面和工作带上以三菱柱单元网格形式划分,网格划分的顺序按工作带-焊合室-坯料,其他部分网格以离工作带越远网格单元尺寸越大的规则划分.
 |
| 图 4 挤压模拟模型 Fig. 4 Simulated model of extrusion |
3 Altair Hyperxtrude挤压模拟结果分析
上述为初始方案(棒料直径210 mm,棒料、模具、料筒预热温度分布为480 ℃、480 ℃、450 ℃,挤压速度为2 mm/s)挤压仿真结果,图 5~图 8分别示出了挤压型材各部分的流速以及流经各处的速度.理论上[13-15],坯料在工作带上的流速越均匀挤压制品端面越平齐,从而型材质量更好,从图 5可以看到在平模部分明显快于分流部分,并在壁厚小的地方流速更快,这是因为在平模处孔大供料快,而在分流部分相对供料较慢,由图 6可以明显反映供料速度,图 7是坯料通过分流孔的速度,也就是分流孔的供料速度,从图 7中可以看出在坯料流经各分流孔时的相对速度,通过合理对比,在分流孔分配上起到主导作用,在流速快的地方可以适当减少分流孔面积;其中图 8反映的是坯料流经工作带时的流速,可以看出在平模处的流速要稍高于分流部分的速度.
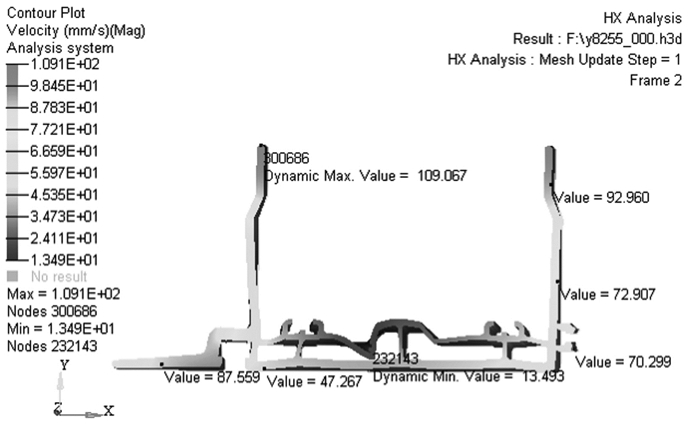 |
| 图 5 型材各部分流速 Fig. 5 Flowing of aluminum profile |
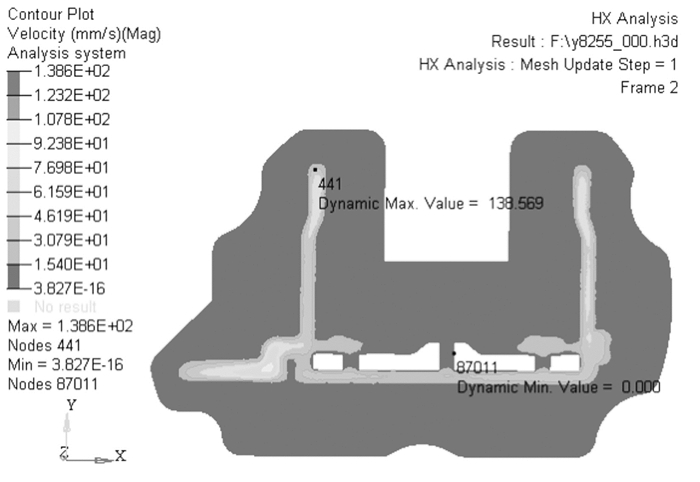 |
| 图 6 供料流速 Fig. 6 Feeding flow rate |
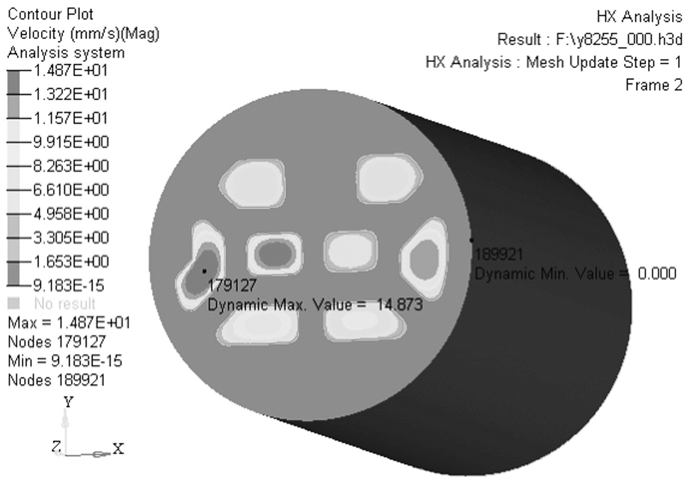 |
| 图 7 分流孔供料流速 Fig. 7 Feed flow rate of diffluent hole |
 |
| 图 8 工作带处流速 Fig. 8 Flow rate of the bearing |
4 Taguchi试验方法分析
利用Hyperxtrude挤压专用模拟软件分别对试验直交表中32组不同的挤压工艺条件下的挤压过程进行仿真模拟,利用公式:
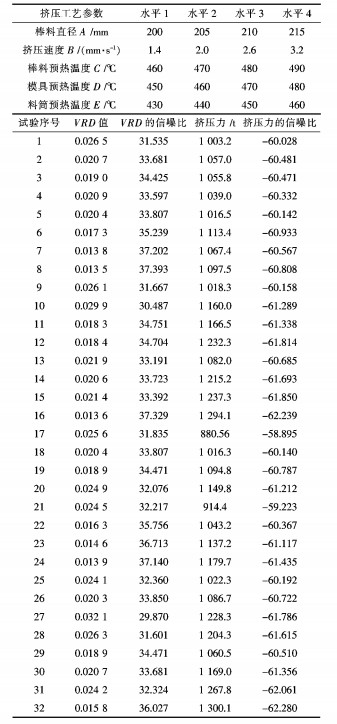
通过模拟out文件获得挤压力大小,同时利用式(4)计算出VRD、挤压力的信噪比,计算结果如表 1.
| 表1 因素水平表 Table 1 Factors and levels of experiments |
 |
| 点击放大 |
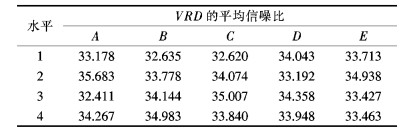
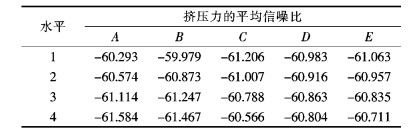
通过模拟每组工艺参数条件下的挤压过程,计算获得挤压型材截面速度均方差VRD和挤压力的信噪比,为了准确分析各工艺参数对型材的影响,利用直观分析原理算出不同水平条件下各组工艺参数的信噪比的平均值具体见表 2、表 3.
| 表2 不同水平下VRD的平均信噪比 Table 2 Average signal-to-noise-ratios of VRD under different levels |
 |
| 点击放大 |
| 表3 不同水平下挤压力的平均信噪比 Table 3 Average signal-to-noise-ratios of extrusion force under different levels |
 |
| 点击放大 |
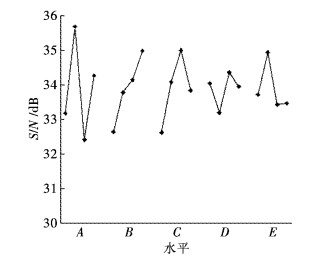
将表 2、表 3不同水平因素的VRD和挤压力信噪比采用直线图的形式表示出来,结果如图 9、图 10,从图 9、图 10中可以看出不同挤压工艺参数对型材截面速度和挤压力有不同的影响规律,根据经验及理论知识可知:型材流经模具出口处的速度越均匀则型材表面质量越好、型材表面缺陷越少;挤压型材所需挤压力越小,挤压所需能耗越小,挤压过程中模具磨损量也越小.因此本研究目标是减小VRD和降低挤压力,故采用信噪比中的望小特性来评价指标的优劣.原理为:信噪比越大,目标变化越小,结果越好.
 |
| 图 9 不同工艺参数对VRD的影响 Fig. 9 Effects of different parameters on VRD |
 |
| 图 10 不同挤压工艺参数对挤压力的影响 Fig. 10 Effects of different extrusion process parameters on extrusion force |
5 结论
以Hyperxtrude软件为模拟载体,基于Taguchi试验分析方法对模拟结果进行计算分析,并由直线趋势图以及望小特性信噪比原理得出以下结论:
1)对于型材截面流动均匀程度指标参数,最佳的挤压工艺参数组合为A2B4C3D3E2,即挤压棒料外径为205 mm、挤压垫速度3.2 mm/s、棒料预先加热温度为480 ℃、挤压模具预先加热温度为470 ℃、挤压筒预先加热温度为440 ℃.
2)对于挤压力指标参数,最佳工艺参数组合为A1B1C4D4E4,即棒料外径为200 mm、挤压垫速度为1.4 mm/s、棒料预先加热温度为490 ℃,挤压模具预先加热温度为480 ℃、挤压筒预先加热温度为460 ℃.
3)在实际生产厂家推荐以及经验制定的挤压参数范围内,改变挤压工艺参数对型材截面速度和挤压力有很大影响,其中改变棒料直径、挤压速度和棒料预热温度对其影响最大,可以通过改变其参数来控制型材质量.
6 结论验证以图 2、图 3模具构造原理加工出实际挤压模具,以上述获得的最佳方案A2B4C3D3E2(型材在模具出口处的流速越均匀型材发生扭拧、翘曲等缺陷就越小)设置挤压工艺参数,首先通过Hyperxtrude进行仿真模拟,获得型材理论形变.然后以上述参数进行实际挤压设计,由华南某厂协助完成试模,选择的挤压设备为1 800 t卧式挤压机如图 11,通过试模获得实际型材制品如图 12.通过对型材制品与有限元模拟结果进行分析,可以得出两者变形趋势较一致,最终获得的型材表面光滑平整,没有出现因过烧而引起的表面斑点;纵向也较平直,没有出现因流速不均匀而引起的弯曲、扭拧、翘曲等宏观缺陷.
 |
| 图 11 1 800 t卧式挤压机 Fig. 11 The 1800 t horizontal extrusion press |
 |
| 图 12 型材制品 Fig. 12 Product of profile |
| [1] | 陈浩.空心铝合金型材挤压过程数值模拟及模具优化方法研究[D].济南:山东大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10422-1012461555.htm |
| [2] | 周飞, 苏丹, 彭颖红, 等. 有限体积法模拟铝型材挤压成形过程[J]. 中国有色金属学报, 2003, 3(1): 65–70. |
| [3] |
Shivpuri R, Momin S. Computer-aided design of dies to control dimensional quality of extruded shaped[J].
Annals of the CIRP, 1992, 41: 275–279. DOI: 10.1016/S0007-8506(07)61203-7. |
| [4] |
Zhou J, Li L, Duszczyk J. Computer simulated and experimentally verified isothermal extrusion of 7075 aluminum through continuous ram speed variation[J].
Journal of Materials Processing Technology, 2004, 146: 203–212. DOI: 10.1016/j.jmatprotec.2003.10.018. |
| [5] |
Lou S M, Zhao G Q, Wang R, et al. Modeling of aluminum alloy profile extrusion process using finite volume method[J].
Journal of Materials Processing Technology, 2008, 206(1/2/3): 481–490. |
| [6] | 王锐, 赵国群, 娄淑梅, 等. 基于非正交结构网格有限体积法的铝型材挤压过程数值模拟关键技术[J]. 塑性工程学报, 2009(2): 134–139. |
| [7] | 王尧, 周照耀, 潘健怡, 等. 基于ALE有限元法的铝型材挤压成形的数值模拟[J]. 锻压技术, 2010(1): 149–153. |
| [8] | 王尧.铝合金型材分流挤压过程的数值模拟研究[D].广州:华南理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10561-2010228088.htm |
| [9] | 倪正顺, 刘石柏, 何畅. 基于HyperXtrude的铝型材挤压成型的数值模拟[J]. 湖南工业大学学报, 2012(2): 38–42. |
| [10] | 王桂龙, 赵国群, 李辉平, 等. 薄壁注塑制品翘曲影响因素分析与工艺优化[J]. 中国机械工程, 2009(4): 488–492. |
| [11] | 孙国栋, 刘长华. 薄壁塑件注射工艺参数的Taguchi方法优化[J]. 模具工业, 2010(8): 51–53. |
| [12] | 王安麟, 傅英超, 刘瑜华, 等. 基于田口方法的电子连接器微颤振磨损自组织模型的优化[J]. 机械工程学报, 2010, 21: 118–123. |
| [13] |
Wu X H, Zhao G Q, Luan Y G, et al. Numerical simulation and die structure optimization of an aluminum rectangular hollow pipe extrusion process[J].
Materials Science and Engineering A, 2006, 435/436: 266–274. DOI: 10.1016/j.msea.2006.06.114. |
| [14] |
Lee R S, Jou J L. Application of numerical simulation for wear analysis of warm forging die[J].
Journal of Materials Processing Technology, 2003, 140: 43–48. DOI: 10.1016/S0924-0136(03)00723-4. |
| [15] | 吴向红.铝型材挤压过程有限体积数值模拟及软件开发技术的研究[D].济南:山东大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10422-2007041396.htm |
 2016, Vol. 6
2016, Vol. 6

