北京科技大学冶金与生态工程学院,北京 100083
基金项目:国家自然科学基金资助项目(50974011,51174021),中央高校基本科研业务费专项资金(FRF-TP-09-003A)
收稿日期:2014-10-15
Experimental study of the activity coefficients of vanadium in liquid copper
School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China
0 引言
钒在钢铁行业中是一种重要和经济的合金元素之一.由于V对C和N具有极强的化学亲和力,V可以溶解在钢中形成氮化物(VN)以及碳化物((FeV)3C,V4C3,and VC),其主要在奥氏体晶界的铁素体中沉淀析出,在轧制过程中能抑制奥氏体的再结晶并阻止晶粒长大,从而起到细化铁素体晶粒、提高钢的机械性能[1-3].钒铁合金常用于传统的钢铁生产工艺流程中,而一种更加经济的方法是直接在冶炼炉中混合加入价格更加低廉的钒氧化物、钒矿和还原剂[4-6].但是无论是哪种方法冶炼钒钢,研究关于钒氧化物在渣中的热力学性质对于优化钢铁生产工艺都十分有必要.
通常采用化学平衡法得到渣中钒氧化物的热力学性质,而为了得到钒氧化物的热力学数据,就需要得到V在参比金属如Cu、Ag中的活度系数.例如,Kazuki Morita等[7]就是通过Cu作为参比金属,得到了铬氧化物在渣中的热力学性质.Holappa等[8]通过Ag作为参比金属,测得渣中铬氧化物的活度.因此,对于研究渣中钒氧化物的热力学性质,在1 873 K附近温度范围的Cu-V体系热力学数据就十分有用.但是,关于V在Cu中的热力学性质研究几乎未见报道.
本文通过固态V2O3与液态Cu的一系列的高温化学平衡实验,测得在1 673 K~1 873 K温度范围内V在Cu液中的活度系数,实验结果对于补充和完善Cu-V体系的热力学数据十分重要.
1 实验
实验在钼坩埚中进行,通过固态V2O3与液态Cu平衡,反应表达式如下:
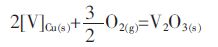
|
(1) |
同时,实验通过严格控制CO/CO2的流量比例控制氧分压,故氧分压可以通过式(2)的平衡氧分压来确定:
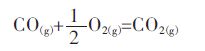
|
(2) |
将式(1)和式(2)相加,得到表达式:
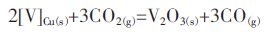
|
(3) |
式(3)的平衡常数表达式表述为:
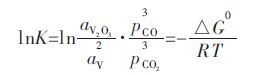
|
(4) |
由Physical Chemistry of High Temperature Technology[9]书中查得式(3)的标准反应吉布斯自由能与温度的关系式如下:
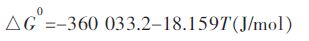
|
(5) |
根据式(4)和式(5),通过不同温度下V在Cu中的含量和CO/CO2的体积比,从而可以算出钒在铜液中的活度系数.
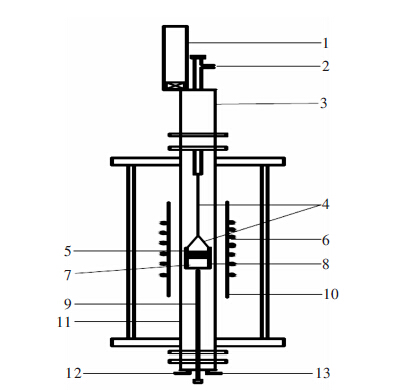
实验所用钼丝炉装置如图 1所示,本实验采用的密闭性能良好并附有水冷腔和快速提升装置的高温钼丝炉,通过2个荷兰Bronkhorst公司高精度数字质量流量控制器严格控制CO和CO2比例来精确控制反应体系的氧分压,采用C型(钨铼5/26)热电偶和日本西曼顿公司的FP21型PID温控仪进行精准控温(温度误差不超过±1 K).利用钼丝使钼坩埚与提升装置连接,在提升装置的帮助下,坩埚可以快速从恒温带提至水冷腔,以保证样品的淬冷效果.
在每次常规实验中,用电子天平称取3 g的Cu和1 g的V2O3.其中Cu被压片并放入钼坩埚底部,V2O3粉末放置于铜片之上,然后将坩埚放置于钼丝炉的恒温带.将钼丝炉密闭后抽真空并缓缓通入氩气,待炉内压力达到一个大气压后重复操作,重复3次以排尽炉内空气.之后通过流量计通入一定比例的CO和CO2的混合气体并开始升温操作.待温度达到平衡温度后,保温适当的时间后,将坩埚快速提升至淬冷腔.待炉内温度冷却至室温之后,取出样品.将Cu-V合金与渣分离后打磨干净,通过ICP-AES检测V在Cu中的含量,通过XRD分析实验的氧化物渣样.实验平衡温度和时间以及检测结果如表 1所示.
表1(Table 1)
|
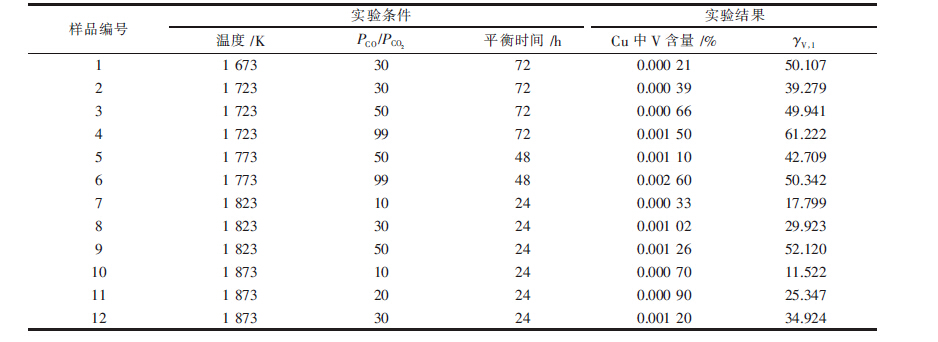
表1 实验条件和结果
|
表1 实验条件和结果
| 样品编号 | 实验条件 | | 实验结果 |
| 温度/K | PCO/PCO2 | 平衡时间/h | | Cu中V含量/% | γv,1 |
| 1 | 1673 | 30 | 72 |
| 0.00021 | 50.107 |
| 2 | 1723 | 30 | 72 | 0.00039 | 39.279 |
| 3 | 1723 | 50 | 72 | 0.00066 | 49.941 |
| 4 | 1723 | 99 | 72 | 0.0015 | 61.222 |
| 5 | 1773 | 50 | 48 | 0.0011 | 42.709 |
| 6 | 1773 | 99 | 48 | 0.0026 | 50.342 |
| 7 | 1823 | 10 | 24 | 0.00033 | 17.799 |
| 8 | 1823 | 30 | 24 | 0.00102 | 29.923 |
| 9 | 1823 | 50 | 24 | 0.00126 | 52.12 |
| 10 | 1873 | 10 | 24 | 0.0007 | 11.522 |
| 11 | 1873 | 20 | 24 | 0.0009 | 25.347 |
| 12 | 1873 | 30 | 24 | | 0.0012 | 34.924 |
|
 |
| 点击放大 |
2 结果和讨论
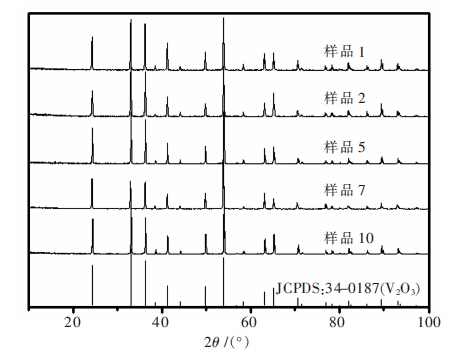
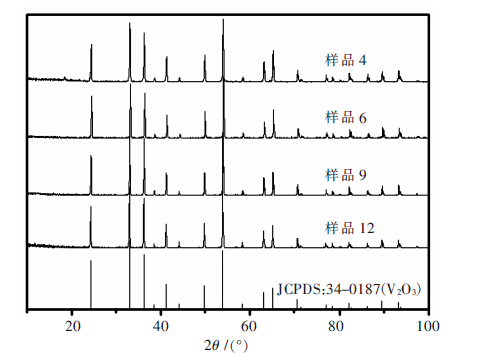
将平衡后的固态V2O3粉末进行XRD衍射分析如图 2和图 3,每个温度下最高和最低氧分压的渣样衍射图与V2O3标准卡片(JCPDS:34-0187)对比发现峰位完全匹配,这表明平衡反应过程中V2O3的晶体结构并未发生变化.
V在液态Cu中的含量通过ICP-AES检测结果列于表 1中.从表 1可以看出,V在液态Cu中的含量非常低,最大的含量不超过3.0×10-5.因此可以将本实验中研究的Cu-V熔体当做稀溶液,从而适用于亨利定律.
如果以上推论成立并且固态V2O3是一种纯化合物,则V在液态Cu中的活度系数可以利用式(3)和式(5)算得,并且应该只与温度有关.但是,从表 1中看出,相同温度下计算所得的V在Cu中活度系数随着氧分压的降低而增大.
由于上述矛盾,查阅V2O3的热力学性质的相关文献资料发现,目前已有大量的科研工作者证实了很多钒氧化物存在氧的非化学计量性[10-11].Katsura等[12-14]通过热重分析法以及淬冷法研究了在1 034 ℃~1 427 ℃下不同氧分压对(V2O3)s.s的影响.所有结果表明V2O3并不是一种纯化合物,而是一种固溶体(V2O3)S.S..因此,(V2O3)S.S.的吉布斯自由能与温度和氧分压有关,上述计算V在Cu中活度系数的方法并不准确.
Youn-Bae Kang[15]提出一种优化的热力学模型,认为(V2O3)S.S.是2种假定的组分V2O2和V2O4溶解在V2O3中的随机混合物,并提出(V2O3)S.S.的标准摩尔吉布斯自由能表达式如下:
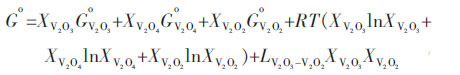
|
(6) |
基于大量的实验数据分析基础上,Youn-Bae Kang得到优化模型参数${{G}^{\text{o}}}_{{{\text{V}}_{\text{2}}}{{\text{O}}_{\text{4}}}}$、${{G}^{\text{o}}}_{{{\text{V}}_{\text{2}}}{{\text{O}}_{\text{2}}}}$、${{L}_{{{\text{V}}_{\text{2}}}{{\text{O}}_{\text{3}}}\text{-}{{\text{V}}_{\text{2}}}{{\text{O}}_{\text{2}}}}}$等见表 2.
表2(Table 2)
|
表2 (V2O3)S.S.固溶体吉布斯自由能模型中的优化
|
表2 (V2O3)S.S.固溶体吉布斯自由能模型中的优化
| 参数名称 | 参数值 |
| LV2O3-V2O3 | -125 520 |
| GV2O30 | 2×G(VO,s)0+962 32 |
| GV2O40 | 2×G0(β-VO2,s)+7 112.8 |
| G(V2O3,s)0 | -1 253 440.71+559.79T-98.09TlnT-1.752 16×10-2T2-2 615 668T-1 (1 200 K<T<2 800 K) |
| G(β-VO2,s)0 | -738 396.904 4+438.781 6T-72.403TlnT-4.654 5×10-3T2+3.733 3×10-9T3+6.79×105T-1 (340K<T<2200K) |
| G(VO,s)0 | -465 796.70+212.57T-37.72TlnT-1.069×10-2T2+2.657 8×10-7T3+512 623.79T-1+3 913.98lnT (298 K<T<2 063 K) |
|
 |
| 点击放大 |
Youn-Bae Kang[15]所提出的(V2O3)S.S.固溶体热力学模型,(V2O3)S.S.固溶体可看做三元系来处理.根据Gibbs-Duhem方程,对于三元系中组元吉布斯自由能可由下列方程式表示,其中 、和分别表示在三元系中各组分的偏摩尔吉布斯自由能:
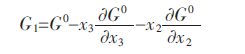
|
(7) |
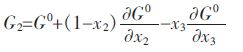
|
(8) |
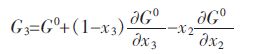
|
(9) |
将优化的(V2O3)S.S.热力学模型公式(6)代入的三元Gibbs-Duhem方程中,可得到各组元的偏摩尔吉布斯自由能表达式:
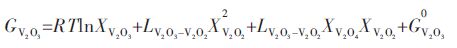
|
(10) |
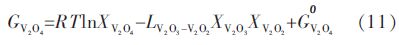
|
(1) |
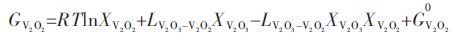
|
(1) |
同时,固溶体(V2O3)S.S.与氧之间存在平衡,表达式如下:
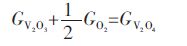
|
(13) |
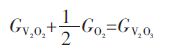
|
(1) |
将式(10)、式(11)和式(12)代入式(13)和式(14),可以得到如下三元非线性方程组:
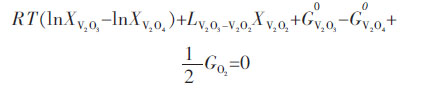
|
(15) |
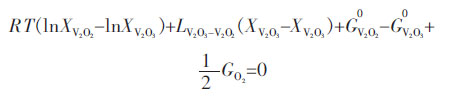
|
(16) |
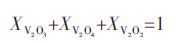
|
(17) |
通过上述非线性方程求解,得到在固定氧分压条件下固溶体(V2O3)S.S.中各组元的摩尔分数.表 3列出计算得出的不同实验温度和氧分压条件下V2O3和V2O2的摩尔分数,其中V2O4由于含量接近于零而未在表 3中列出.从表 3中可以看出,在当前实验条件下,氧分压越高,氧的非化学计量性就越小.根据计算所得组元V2O3和V2O2的摩尔分数,通过式(6)和式(10)计算得到固溶体(V2O3)S.S.的标准摩尔吉布斯自由能和V2O3的偏摩尔吉布斯自由能.根据表 3中列出的数据和表 4中各化合物的相对摩尔吉布斯自由能数据[16],算出式(3)的吉布斯自由能变化.另外,通过Youn-Bae Kang[15]提出的热力学模型计算所得V在Cu中的活度系数也列于表 3.尽管计算所得在相同温度下V在Cu中的活度系数仍然不是常数,但相对于表 1计算得到的数据更加相互接近.
表3(Table 3)
|
表3 (V2O3)S.S.中V2O3和V2O2的摩尔分数、(V2O3)S.S.的标准吉布斯自由能、V2O3的偏摩尔吉布斯自由能和计算出的${{\gamma }_{\text{V}\text{2}}}$
|
表3 (V2O3)S.S.中V2O3和V2O2的摩尔分数、(V2O3)S.S.的标准吉布斯自由能、V2O3的偏摩尔吉布斯自由能和计算出的${{\gamma }_{\text{V}\text{2}}}$
| 样品编号 | XV2O3 | XV2O2 | GV2O30 | G | γV,2 |
| 1 | 0.932 | 0.068 | -1 561 235.9 | -1 587 160.2 | 29.677 |
| 2 | 0.928 | 0.073 | -1 577 130.7 | -1 603 622.4 | 23.169 |
| 3 | 0.911 | 0.089 | -1 569 315.3 | -1 604 212.7 | 28.882 |
| 4 | 0.886 | 0.114 | -1 559 503.7 | -1 605 234.9 | 34.163 |
| 5 | 0.905 | 0.095 | -1 583 392.5 | -1 621 040.3 | 24.719 |
| 6 | 0.88 | 0.12 | -1 573 356.8 | -1 622 127.9 | 27.941 |
| 7 | 0.95 | 0.05 | -1 617 498.1 | -1 636 308.4 | 10.569 |
| 8 | 0.918 | 0.082 | -1 604 996.6 | -1 637 376.6 | 17.152 |
| 9 | 0.9 | 0.1 | -1 598 060.8 | -1 638 069.3 | 29.201 |
| 10 | 0.947 | 0.053 | -1 633 318.8 | -1 653 423.3 | 6.843 |
| 11 | 0.926 | 0.074 | -1 625 236.3 | -1 654 107.3 | 14.727 |
| 12 | 0.913 | 0.087 | -1 620 124.8 | -1 654 590.2 | 19.979 |
|
 |
| 点击放大 |
表4(Table 4)
|
表4 各化合物的相对摩尔吉布斯自由能数据 (J·mol-1)
|
表4 各化合物的相对摩尔吉布斯自由能数据 (J·mol-1)
| 参数名称 | 参数值 |
| G(V,s)0 | -8 658.94+151.795T-26.807TlnT+6.7×10-5T2+9.6×104T-1-6.067×10-7T3 (298 K<T<<2 190 K) |
| G(CO,g)0 | -203 680.536+609.464T+0.003T2+770 627.667T-1+32 063.316lnT-10 357.02 T1/2-90.754TlnT (298 K<T<1 700 K)-224 220.539+142.324T+5 816 543.22T-1+20 893.908lnT-2 749.1071/2-44.086TlnT (1 700 K<T<6 000 K) |
| G(CO2,g)0 | -415 578.806+642.768T+0.002T2+2 0124.522T-1-6 993.149T1/2+11 004.741lnT-103.344TlnT (298 K<T<2 000 K) |
|
 |
| 点击放大 |
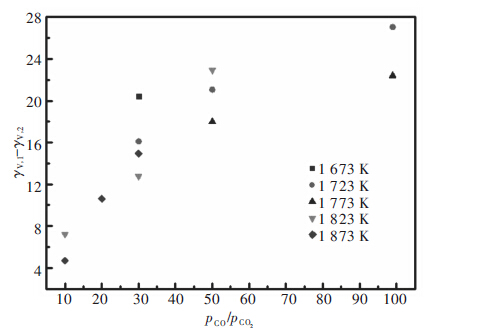
为了比较和的差别,以为横坐标,为纵坐标作图 3.其中,活度系数是通过E. T. Turkdogan[9]书中热力学数据结合实验值计算所得,活度系数是通过Youn-Bae Kang[15]提出的热力学模型计算所得.从图 3可以看出,数值小的点,都是在实验最低CO/CO2流量比情况下得到的.也就是说,氧分压越高,实验值与采用热力学模型计算得到的活度系数值差距越小,误差越小,可信度越高.综上所述,在氧分压较高的条件下,氧的非化学计量性和采用2种方法计算得到的活度系数差别都很小.因此,在较高氧分压下得到的不同温度V在Cu液中的活度系数更可靠.
Figure 3.JPG
图 3 与的关系图
将每个温度下最高氧分压对应的V在Cu中活度系数与温度的关系作图 4,从图 4中可以看出两者之间存在很好的线性关系.由于在最高氧分压下,V在Cu液中含量均小于1.0×10-5,所以可以把Cu-V熔体看成稀溶液.因此,关系式也可以被认为是V在Cu液中活度系数的亨利常数与温度T的关系,并拟合得到:
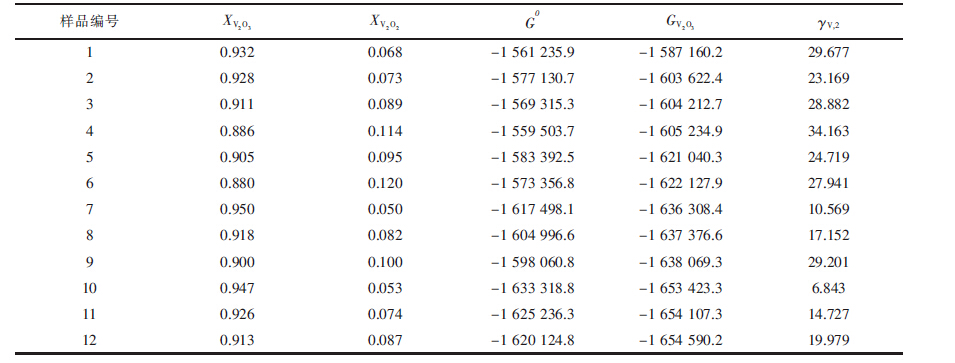
实验采用V2O3与Cu进行平衡,而并非其他钒氧化物,其原因如下:从V-O体系图[15]看出,数值相对V2O3高和低的钒氧化物为VO和V3O5.VO本身也是一种固溶体,如果采用VO与Cu平衡,就需要用本文相同的处理方法计算.而对于V3O5,它虽然是一种化学计量性化合物,但是在1 873 K下的平衡氧分压要高于10-5atm,在如此高氧分压条件下,达到平衡时V在Cu中的含量可以会非常低,不便测定.因此,V2O3是与Cu液进行平衡,测定V在Cu液中的活度系数的最合适化合物.
3 结 论
实验用V2O3与Cu平衡,通过Youn-Bae Kang[15]提出的(V2O3)S.S.固溶体吉布斯自由能模型,测得1 673 ~1 873 K下V在Cu液中活度系数.每一温度下最高氧分压对应V在Cu中的活度系数作为,其对数与温度的关系式如下:
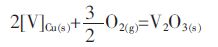
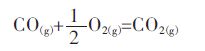
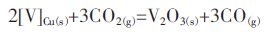
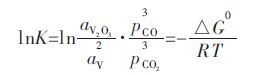
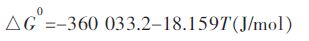

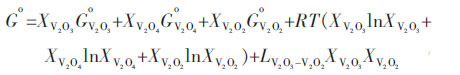

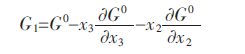
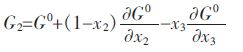
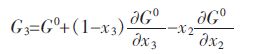
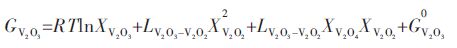
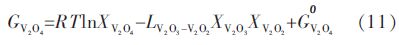
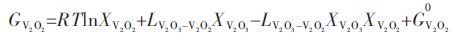
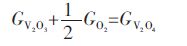
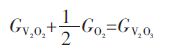
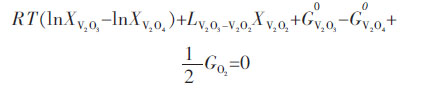
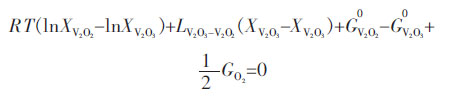
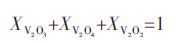


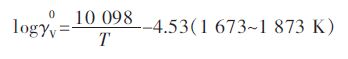
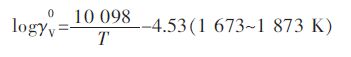
 2015, Vol. 6
2015, Vol. 6


