| 基于HHT方法的微差爆破延时识别 |
2. 新余良山矿业责任有限公司,江西 新余 338001
2. Xinyu Liangshan Mining Co. Ltd., Xinyu 338001, China
因控制需求,微差爆破被广泛应用于露天爆破、拆除爆破和地下爆破等工程.精确的微差时间,是达到优良爆破效果的前提和保证[1],但微差雷管本身存在着一定误差和合格率问题,相邻段别雷管甚至存在“跳段”现象,致使起爆顺序混乱,爆破效果和爆破安全达不到设计要求[2-4].
众多学者对微差爆破延时识别进行研究,取得了诸多成果,先后出现了八线示波器和金属拉线方法[5]、小波模极大值法[6]和小波时-能密度等方法[7].但前者操作复杂,精度有限;小波类方法借助实测爆破振动信号进行识别,取得了不错的效果,但存在分解度和小波基选择问题[8-9],不同的分解尺度和小波基,识别结果亦有差异.为此,采用HHT方法对微差爆破进行延时识别研究.
1 HHT方法简介 1.1 EMD分解HHT(Hilbert-Huang Transform,简称HHT)是N.E.Huang等[10]提出的信号处理方法,由EMD(Empirical Mode Decomposition,简称EMD)分解和Hilbert变换组成.针对爆破振动类非平稳数据,EMD分解无需先验基,能随信号的变化自适应分解成有限若干IMF分量,其原理如下[11-12]:
步骤1:原始信号为S(t)(t=1,2,…,n,为时间采样点数),设定IMF分量的判断条件:①极点数和零点数差值不超过1;②上、下包络线以时间轴为准,局部对称,也即均值为0.
步骤2:确定S(t)所有极值点,通过3次样条插值获取S(t)的上包络线Smax(t)和下包络线Smin(t),并求取上、下包络线的均值曲线m(t):
| $m(t) = \frac{1}{2}\left[ {{S_{\max }}(t) + {S_{\min }}(t)} \right]$ |
将m(t)从S(t)中输出,则剩余值h1(t)为:
| ${h_1}(t) = S(t) - m(t)$ |
步骤3:如果h1(t)符合IMF分量判断条件,将其作为第一个IMF分量输出,否则代替S(t)重复筛选过程,直至k(k=1,2,…,n)次迭代后,剩余值hk(t)成为一个IMF,即IMF1(t)=hk(t).
将IMF1(t)输出后,第一阶段的剩余信号R1(t)为:
| ${R_1}(t) = S(t) - IM{F_1}(t)$ |
步骤4:对R1(t)继续重复步骤2、步骤3的筛选工作,从高频到低频依次输出IMF2(t)、IMF3(t)、…、IMFi(t),直至最后的残差:
| ${R_i}(t) = {R_{i - 1}}(t) - IM{F_i}(t)$ |
当Ri(t)再也无法分解出新的IMF分量时,终止筛选工作.那么信号S(t)为IMF1(t)、IMF2(t)、…、IMFi(t)及余量Ri(t)之和:
| $S(t) = \sum\limits_{i = 1}^n {IM{F_i}(t)} + {R_i}(t)$ |
EMD分解后获取若干个IMF分量,对各分量作Hilbert变换:
| $H\left[ {IMF(t)} \right] = \frac{1}{{\rm{ \mathsf{ π} }}}PV\int_{ - \infty }^{ + \infty } {\frac{{IMF(t')}}{{t - t'}}} {\rm{d}}t'$ |
其中,PV为柯西主值(Cauchy Principal Value),因此,构造信号z(t):
| $z(t) = IMF(t) + jH\left[ {IMF(t)} \right] = a(t){e^{j\varphi (T)}}$ |
其中,a(t)为z(t)的幅值函数,也即,分量IMF(t)的包络;φ(t)为相位函数:
| $\begin{array}{l} a(t) = \sqrt {IM{F^2}(t) + {H^2}\left[ {IMF(t)} \right]} \\ \varphi (t) = \arctan \frac{{H\left[ {IMF(t)} \right]}}{{IMF(t)}} \end{array}$ |
于是,瞬时频率可表示为:
| $f(t) = \frac{{\omega (t)}}{{2{\rm{ \mathsf{ π} }}}} = \frac{1}{{2{\rm{ \mathsf{ π} }}}} \times \frac{{{\rm{d}}\varphi (t)}}{{{\rm{d}}(t)}}$ |
如果将趋势分量R(t)忽略,Re表示取实部,则S(t)可表示为:
| $S(t) = \mathit{Re}\sum\limits_{i = 1}^n {{a_i}(t)} {e^{j{\varphi _i}(t)}} = \mathit{Re}\sum\limits_{i = 1}^n {{a_i}(t)} {e^{j\int {{\omega _i}(t)} {\rm{d}}(t)}}$ |
表达了在时间和频率平面上瞬时振幅的分布规律,将其定义为Hilbert谱:
| $H(\omega ,t) = \mathit{Re}\sum\limits_{i = 1}^n {{a_i}(t)} {e^{j\int {{\omega _i}(t)} {\rm{d}}(t)}}$ |
依据巴什瓦(Parseval)定理[13],可将|IMFi(t)|2视作是各IMF分量的能量密度,如此,H2(ω,t)同样具备能量密度的物理意义,将其称作Hilbert能量谱,则在Hilbert-Huang变换前后,信号的能量应该守恒,也即:
| ${\int_{ - \infty }^{ + \infty } {\left| {S(t)} \right|} ^2}{\rm{d}}t = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } H } (\omega ,t){\rm{d}}\omega {\rm{d}}t$ |
由此定义:
| $IE(t) = \int_\omega {{H^2}(\omega ,t)} {\rm{d}}\omega $ |
表达了信号的频带能量随时间的分布情况.
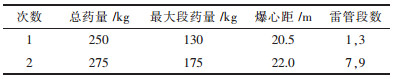
2 MATLAB信号仿真某矿采用水平深孔阶段矿房法采矿,对其某2次采场崩矿进行爆破振动监测,见图 1,信号S1和S2分别为第1次和第2次监测所得,详细爆破信息见表 1.
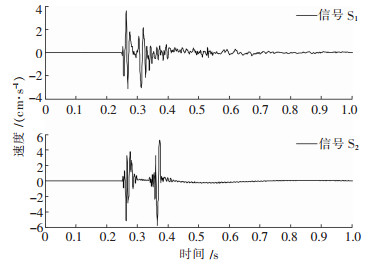 |
| 图 1 原始信号 |
| 表1 爆破信息 |
 |
| 点击放大 |
以S1为例,对其进行EMD分解,获取了9个按照频率高低依次排列的IMF分量和一个余量R,见图 2(篇幅有限,仅列前5个IMF分量).其中,IMF1的频率最大,0.24~0.4 s存在衰减,但整个时间坐标轴分散着少量噪声,是相对高频部分;IMF2的波形衰减明显,幅值最大,是与真实信号相关性最大的分量;IMF3~IMF5分量的幅值已大幅减小,携带真实信号的信息已逐渐减小.
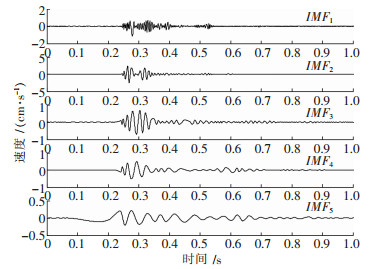 |
| 图 2 EMD分解 |
3 微差延时识别
在微差爆破中,每段雷管的起爆就意味着炸药能量的释放,引发测点爆破振动信号速度或者能量突增[14-16].由此可知,获取爆破主振分量的幅值包络线或瞬时能量曲线,寻找包络线或能量突峰点并计算对应的起爆时刻,就能获取各段雷管的实际延期时间,分别定义为微差爆破延时的幅值包络线识别法和瞬时能量识别法.
经EMD分解和识别,信号S1和S2均是IMF2幅值大,波形衰减明显,为主振分量,携带了爆破的大部分信息,图 3和图 4分别是信号S1和S2的IMF2分量幅值包络线.图 5和图 6则分别是信号S1和S2的瞬时能量.
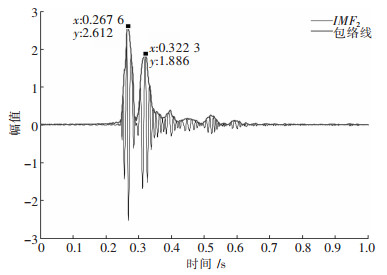 |
| 图 3 IMF2(S1)幅值包络线 |
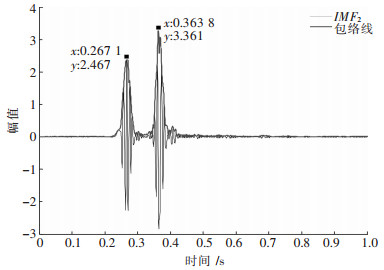 |
| 图 4 IMF2(S2)幅值包络线 |
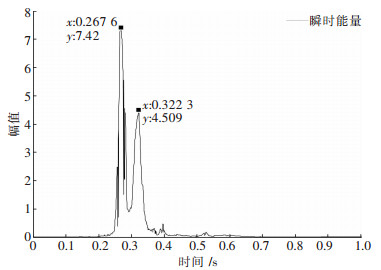 |
| 图 5 瞬时能量(S1) |
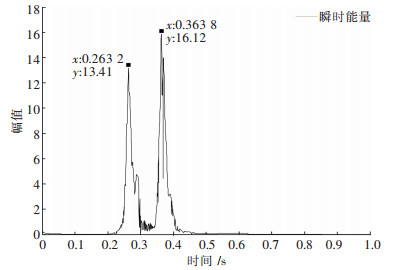 |
| 图 6 瞬时能量(S2) |
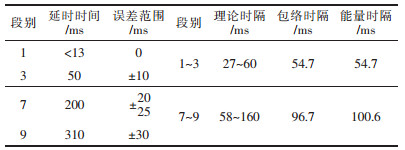
图 3~图 6中突峰点计算可知,由幅值包络线法和瞬时能量法识别的信号S1的两段雷管起爆时刻相同,分别为0.267 6 s和0.322 3 s,延时时间为0.054 7 s;由幅值包络线法识别的信号S2的两段雷管起爆时刻分别为0.267 1 s和0.363 8 s,延时时间为0.096 7 s,由瞬时能量法识别的信号S2的两段雷管的起爆时刻分别为0.263 2 s和0.363 8 s,延时时间为0.100 6 s.实际爆破设计使用的是国产第二系列毫秒延期雷管,对比微差雷管的理论延时和实测间隔时间(见表 2),可知幅值包络线法和瞬时能量法识别的延时时间都在理论值内,该批次雷管精度可靠,矿山可放心使用,也说明这2种方法用于识别微差爆破延时可行.
| 表2 延时计算 |
 |
| 点击放大 |
4 结论
借助MATLAB工具,基于某矿崩矿爆破实测数据,对微差爆破延时时间进行识别研究,得出了以下结论:
1)EMD分解具有自适应性,经Hilbert变换后,可以有效方便地获取幅值包络线和瞬时能量,为微差爆破延时时间识别提供基础.
2)幅值包络线法和瞬时能量法识别的微差爆破延时时间都在理论值内,证明该批次雷管安全可靠,也说明这2种方法识别微差爆破延时可行,为微差爆破延时识别提供了方法.
3)虽然幅值包络线法和瞬时能量法均可用于微差爆破延时识别,但识别结果有所差异(如信号S2).当信号的信噪比较低时,瞬时能量法识别易受噪声能量干扰,出现错误突峰点或突峰点被噪声淹没无法识别现象,因此信号应先进行去噪处理;EMD分解也会出现多个接近的分量,爆破信息被分散,没有绝对主振分量,此时重构多个相近分量形成爆破振动优势分量,然后再提取幅值包络线进行延时识别.
| [1] | 戴俊. 爆破工程[M]. 北京: 机械工业出版社 , 2007. |
| [2] | 凌同华, 李夕兵. 基于小波变换的时-能分布确定微差爆破的实际延迟时间[J]. 岩石力学与工程学报, 2004, 23(13): 2266–2270. |
| [3] | 陈银鲁.爆破震动信号的能量分析方法及其应用研究[D].杭州:浙江大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10335-2010050587.htm |
| [4] | 管志强, 张中雷, 王林桂, 等. 复杂环境大区露天深孔台阶爆破技术在岙山油库区开挖中的应用[J]. 爆破, 2011, 28(2): 63–67. |
| [5] | 范作鹏, 钱守一, 李启月. 微差爆破实际延迟时间识别方法比较与优选[J]. 矿冶工程, 2011, 32(3): 4–8. |
| [6] | 凌同华, 李夕兵. 用小波变换识别微差爆破中的实际延迟时间[J]. 湖南科技大学学报(自然科学版), 2004, 19(2): 21–23. |
| [7] | 凌同华, 李夕兵, 戴塔根. 基于小波变换的时-能密度法优选微差延期时间[J]. 重庆建筑大学学报, 2006, 28(2): 36–39. |
| [8] | 赵明生, 梁开水, 罗元方, 等. EEMD在爆破振动信号去噪中的应用[J]. 爆破, 2011, 28(2): 17–20. |
| [9] | 张义平, 李夕兵. Hilbert Huang变换在爆破震动信号分析中的应用[J]. 中南大学学报, 2005, 36(5): 882–887. |
| [10] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].
Proceedings of the Royal Society of London A, 1998, 454: 903–995. DOI: 10.1098/rspa.1998.0193. |
| [11] | 张义平.爆破震动信号的HHT分析与应用研究[D].长沙:中南大学, 2006. http://www.oalib.com/references/17512316 |
| [12] | 王红军, 万鹏. 基于EEMD和小波包变换的早期故障敏感特征获取[J]. 北京理工大学学报, 2013, 33(9): 945–950. |
| [13] | 周德廉, 邵国友. 现代测试技术与信号分析[M]. 徐州: 中国矿业大学出版社 , 2005. |
| [14] | 付晓强, 张世平, 张昌锁. 复线隧道爆破震动信号的HHT分析[J]. 工程爆破, 2012, 18(3): 5–8. |
| [15] | 钱守一, 李启月. 微差爆破实际延迟时间的HHT瞬时能量识别法[J]. 矿业研究与开发, 2012, 32(2): 113–116. |
| [16] | 刘金川, 方向, 冯伟涛. 基于HHT方法的微差爆破延期时间识别与应用[J]. 山西建筑, 2011, 37(4): 91–93. |
 2015, Vol. 6
2015, Vol. 6


