| 某矿井下浅孔毫秒延时爆破地表震动的数值模拟研究 |
某地下铀矿山采用浅孔留矿法开采,矿床所处地层主要岩性为中粒“小斑状”黑云母花岗岩和中粒黑云母花岗岩.矿区上部地表为一村落,主要分布有土坯房、一层或二层砖混结构房以及水稻田,标高约为260 m.为了研究井下生产爆破时地表的震动强度,确保地表民房的爆破震动安全,采用LS-DYNA有限元数值模拟和现场实测相结合的方法对某次具有代表性的生产爆破下的地表震动强度进行了分析研究.
该次生产爆破使用2#岩石硝铵炸药,孔距a=700~900 mm,孔深L=2~2.2 m,矩形布置.采用毫秒延时起爆,共分5段,每段药量分别为:73.5 kg (1段)、31.5 kg (3段)、30.45 kg (5段)、31.5 kg (7段)、84 kg (9段),爆破总药量250.95 kg.
1 爆破现场测试对本次生产爆破采用加拿大生产的Blastmate Ⅲ爆破测振仪进行了现场测试,采场标高185.6 m,在地表按图 1布置5个测点(测点1、2、3、4、5距采场中心水平距离分别42 m、156 m、248 m、276 m、289 m).测振仪触发值设置为0.051 cm/s,采样频率均为2 048次/s,单个事件监测持续时间为3 s,斜距及测试结果见表 1.
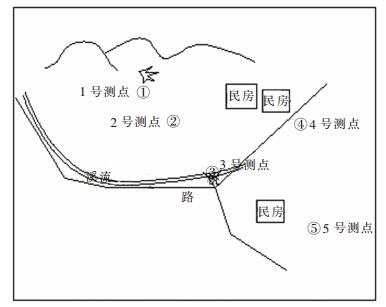 |
| 图 1 各测点地表布置示意图 |
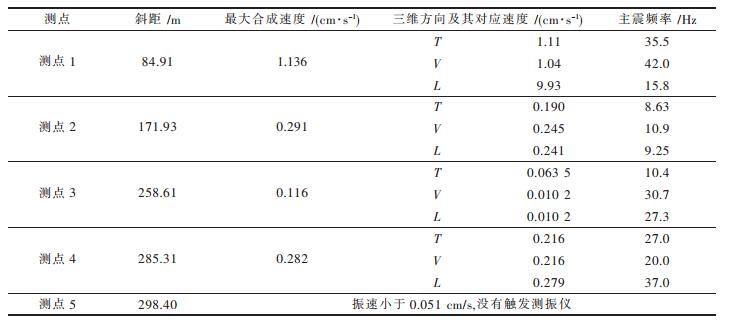
| 表1 各测点实测振速峰值 |
 |
| 点击放大 |
2 LS-DYNA程序及模型材料的选择 2.1 LS-DYNA程序及算法简介
DYNA在J.O.Hallquist主持下由劳伦斯实验室与利维莫尔国家实验室合作开发研发完成,内嵌100多种材料与43种材料模型(能够直接输入的材料模型约30种).其主要计算方法有3种,分别为拉格朗日法(Lagrange)、欧拉法(Euler)与ALE算法.其中ALE算法结合Lagrange算法与Euler算法的优点,是DYNA中多物质、大变形问题的常用算法[1-5].
本次研究中,Lagrange阶段单元采用单点积分计算,即按照时步t=0, Δt1, Δt1+Δt2, …, t+Δt进行求解,运动方程为:
| $ M\ddot x\left( t \right) = P\left( {x, t} \right)-F\left( {x, \ddot x} \right) = H $ | (1) |
式(1)中,
| $ {{\dot \varepsilon }_1} = \frac{{\partial {{\dot x}_1}}}{{\partial {x_1}}}, {{\dot \varepsilon }_2} = \frac{{\partial {{\dot x}_2}}}{{\partial {x_2}}}, {{\dot \varepsilon }_3} = \frac{{\partial {{\dot x}_3}}}{{\partial {x_3}}} $ | (2) |
| $ \begin{array}{l} {{\dot \varepsilon }_{12}} = \frac{1}{2}\left( {\frac{{\partial {{\dot x}_1}}}{{\partial {x_2}}} + \frac{{\partial {{\dot x}_2}}}{{\partial {x_1}}}} \right), {{\dot \varepsilon }_{23}} = \frac{1}{2}\left( {\frac{{\partial {{\dot x}_2}}}{{\partial {x_3}}} + \frac{{\partial {{\dot x}_3}}}{{\partial {x_2}}}} \right), \\ {{\dot \varepsilon }_{31}} = \frac{1}{2}\left( {\frac{{\partial {{\dot x}_3}}}{{\partial {x_1}}} + \frac{{\partial {{\dot x}_1}}}{{\partial {x_3}}}} \right) \end{array} $ | (3) |
对流阶段采用有限体积法计算通过单元边界的通量,计算采用Van Leer对流算法,因为这种算法不仅具有二阶精度,而且具备总变差递减性质[9-11].由于二阶精度的中心差分法进行积分计算虽可极大减少计算量,但可能引起零能模式或称沙漏状态,故需采用沙漏阻尼进行控制,对于沙漏控制可采用缺值算法进行[10-15],即认为单元各节点处沿Xi方向的沙漏黏性阻尼为:
| $ {f_{ik}} = {a_k}\sum\nolimits_{j = 1}^4 {{h_{ij}}{\mathit{\Gamma }_{jk}}} $ | (4) |
其中i=1, 2, 3;k=1, 2, …, 8.
式(4)中,负号表示沙漏阻尼方向与模态变形方向相反;hik为沙漏模态的模,计算式为:
| $ {h_{ik}} = \sum\nolimits_{k = 1}^8 {{{\dot x}_i}} {\mathit{\Gamma }_{jk}} $ |
1)岩石材料及模型.由于该矿床岩体物理力学性质复杂,为了方便研究,数值计算模型在工程实际基础上选用理想花岗岩做为研究材料, 并采用弹塑性材料模型[12-14]定义该材料,其主要物理力学参数见表 2.
| 表2 花岗岩主要物理力学参数表 |
 |
| 点击放大 |
2)炸药材料及炸药模型.炸药选用2#岩石炸药, 主要参数见表 3,采用MAT_HIGH_EXPLOSIVE_ BURN模型.本文采用JWL方程描述炸药状态.其状态方程为:
| $ P = A\left( {1-\frac{\omega }{{{R_1}V}}} \right){e^{-V{R_1}}} + B\left( {1-\frac{\omega }{{{R_2}V}}} \right){e^{ - V{R_2}}} + \frac{{\omega E}}{V} $ | (5) |
| 表3 炸药主要参数表 |
 |
| 点击放大 |
式(5)中, V为相对体积;E为内能参数,A、B、R1、R2、W为特征参数.
3)土体材料及模型.土壤采用MAT_SOIL_AND_ FOAM材料模型,其主要物理力学参数见表 4.
| 表4 土体主要参数表 |
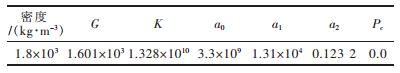 |
| 点击放大 |
3 LS-DYNA模型的建立及计算 3.1 LS-DYNA模型的建立
根据实际需求建立166 m中段采场大小为300 m×30 m×74 m的数值模型.为减少计算量并保证计算准确性,对计算模型做如下处理:
1) 将同段起爆的所有炸药折算为集中药包进行处理;
2) 尽量将集中药包在采场内均布,使爆破效果尽可能与实际相符;
3) 为了减少网格密度采用m-kg-s单位制,为了适应炸药量将炸药周围网格进行细化处理.
由于六面体单元网格计算较为准确,故将实体模型划分为六面体单元[15],同时为了实现六面体网格单元的再划分,采用扫掠法对实体模型进行网格划分,最后形成有限元模型如图 2,模型加密部位为炸药所处位置,炸药周围网格细化如图 3.由于共分为5段进行起爆,故建立5个集中药包.
 |
| 图 2 有限元模型图 |
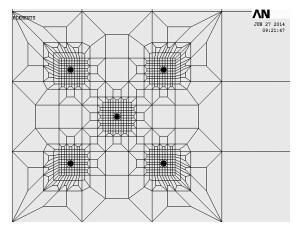 |
| 图 3 炮孔附近加密图 |
3.2 数值计算结果
在数值模型中按照实际测试距离布置设立5个数值计算点,具体位置见图 4(其中点4 883、3 964、4 061、4 113与4 137分别对图 5~图 8中曲线1、2、3、4与5).对各测点起爆后2 s振动速度进行数值模拟计算,绘制爆后0.5 s内三维合成以及水平径向、垂直方向、水平切向的振速-时间曲线, 分别见图 5~图 8;各观测点的振速峰值见表 5.
 |
| 图 4 数值计算中测点布置图 |
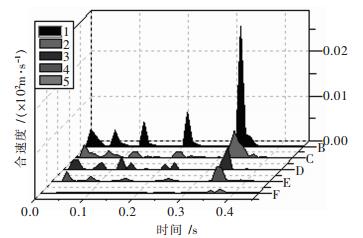 |
| 图 5 各测点合速度-时间曲线 |
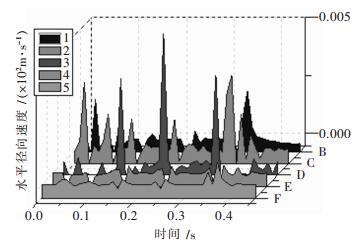 |
| 图 6 各测点水平径向(L)速度-时间曲线 |
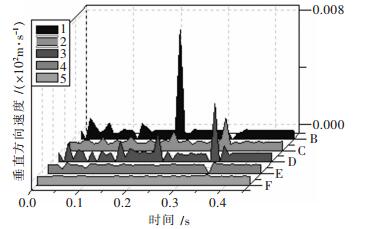 |
| 图 7 各测点垂直方向(V)速度-时间曲线 |
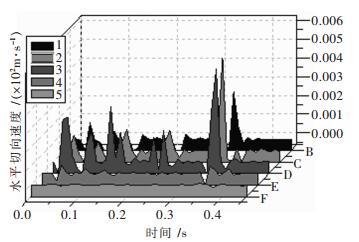 |
| 图 8 各测点水平切向(T)速度-时间曲线 |
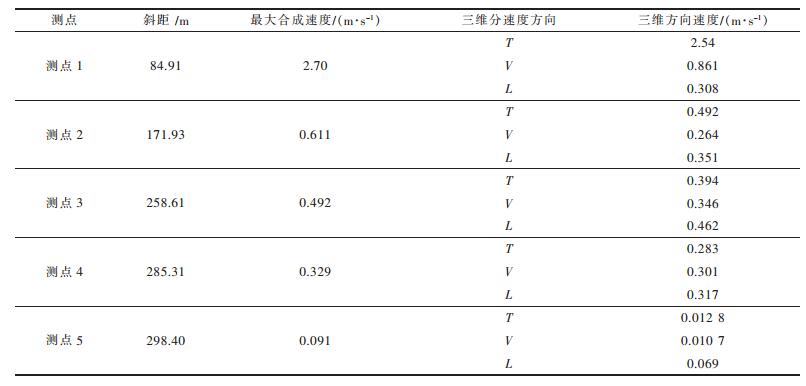
| 表5 各测点模拟计算振速峰值 |
 |
| 点击放大 |
由图 5和表 5可知,测点1的三维合成振速最高,且5个测点合成振动峰值依次降低,由图 5~图 8可知爆破振动持续时间约450 ms左右.
对比分析表 1与表 5可知,数值计算所得垂直方向、水平切向、水平径向及三维合成速度均比实际测量值略大.
由于该地民房主要为土坯和砖石结构,且爆破主振频率为10~50 Hz,根据我国GB6722-2003《爆破安全规程》可知,此种情况下允许振速为0.7~1.2 cm/s.只有测点1的数值模拟计算值及实际测量值超过了该标准,但通过现场考察可知,该测点到最近民房的距离超过100 m,而最近民房大约在测点4的位置,因此,采用在该药量参数和同类现场条件下的井下生产爆破符合安全标准.
4 分析与结论1) 数值计算和实际测试均表明,本次药量参数可供166 m中段采场生产爆破借鉴,但若采场水平延伸到民房正下方附近时该药量需适当的减少,否则会对民房造成危害,具体最大单段药量可由萨道夫斯基公式求得.
2) 由于测点3布置在一条小水沟旁边,该水沟在一定程度上起到了降震沟作用,使得该点实测值相比距爆心更远的测点4的实测值较小.
3) ANSYS/LS-DYNA有限元数值结果较实测值略偏大,其原因是数值模拟计算过程中对同段起爆的多孔装药按集中药包进行了简化处理,这使得原本分散装药的炸药变得集中,从而爆破震动加强;同时地表现场水田可起到一定的降震作用,而数值模拟中只是作为均质的表土处理.但整体上看,采用ANSYS/LS-DYNA数值模拟法对爆破震动强度的预测不失其理论意义及指导价值.
| [1] | 石少卿, 康建功, 江敏, 等. L S-DYNA在爆炸与冲击领域内的工程应用[M]. 北京: 中国建筑工业出版社 , 2011. |
| [2] | 张智超, 刘汉龙, 陈育民, 等. 爆破地震的数值模拟及爆破振动规律分析[J]. 郑州大学学报(工学版), 2012, 33(5): 10–15. |
| [3] | 夏祥, 李海波, 李俊如, 等. 岩体爆生裂纹的数值模拟[J]. 岩土力学, 2006, 27(11): 1987–1991. |
| [4] | 梁斌, 陈忠富, 卢永刚. 柱形装药在混凝土中爆炸波传播数值模拟[J]. 弹箭与制导学报, 2008, 28(4): 93–95. |
| [5] | 肖明, 张雨霆, 陈俊涛, 等. 地下洞室开挖爆破围岩松动圈的数值分析计算[J]. 岩土力学, 2010, 31(8): 2613–2618. |
| [6] | 杨海书, 林从谋, 林丽群, 等. 复杂结构体系下隧道爆破振动对房屋影响的试验研究[J]. 山东科技大学学报(自然科学版), 2011(2): 65–79. |
| [7] | 张智超, 陈育民, 刘汉龙. 微差爆破模拟天然地震的数值分析与效果评价[J]. 岩土力学, 2013(1): 265–274. |
| [8] | 李宁, 张承客, 周钟. 边坡爆破开挖对邻近已有洞室影响研究[J]. 岩石力学与工程学报, 2012(增刊2): 3471–3476. |
| [9] | 肖文芳, 肖文涛, 房泽法. 地铁隧道掘进爆破地表振动效应研究[J]. 工程爆破, 2012, 18(2): 46–49. |
| [10] | 史秀志, 曾志林, 田建军, 等. 深井开采爆破对巷道影响的数值模拟分析[J]. 工程爆破, 2010, 16(2): 10–14. |
| [11] | 时党勇, 李裕春, 张胜民. 基于ANSYS/LS-DYNA8.1进行显式动力分析[M]. 北京: 清华大学出版社 , 2005. |
| [12] | 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社 , 2005. |
| [13] | 何涛. ANSYS10.0/LS-DYNA非线性有限元分析实例指导教程[M]. 北京: 机械工业出版社 , 2007. |
| [14] | 尚晓江, 苏建宇, 魏久安, 等. ANSYS/LS-DYNA动力分析方法与工程实例[M]. 北京: 北京水利水电出版社 , 2006. |
| [15] |
Schneidersr. A-grid algorithm for the generation of hexahedral element meshes[J].
Engineering with computers, 1996(12): 168–177. |
 2014, Vol. 5
2014, Vol. 5

