| 微孔陶瓷管孔隙率的测定及表面润湿性研究 |
2. 北京矿冶研究总院, 北京 100160
2. Beijing General Research Institute of Mining & Metallurgy, Beijing 100160, China
随着我国对改善大气环境质量工作的推进,研究开发高效捕集烟气中细颗粒的装置可以有效缓解冶金行业所面临的环保危机,同时也能大幅度提高空气质量.冶金行业各种对烟气粉尘的过滤装置不能高效捕集细颗粒.微孔陶瓷过滤管具有耐高温、耐腐蚀、耐清洗、机械强度大、结构稳定不变形和寿命长等诸多优点,是一种非常优质的过滤材料,在液相分离和气固分离中都有很好的效果[1].国外对于陶瓷管的研究大致始于1940年,在二战期间主要应用于铀的同位素分离的核工业中.1990年开始,陶瓷管应用于以无机微滤膜和超滤膜为主的液体分离过程中,美国、日本、德国等在陶瓷膜的开发和应用方面发展极为迅速.
研究金属对陶瓷的润湿性[2-3]对开发新型金属/陶瓷体系,探寻材料的制备技术,制备高性能金属/陶瓷复合材料等有重要意义[4].杨龙龙等[5]利用先进的改良座滴法系统研究了2种常见稀土元素La、Ce与陶瓷基板的润湿性及界面结构,为制备高性能的金属/陶瓷复合材料提供基础数据与理论指导.刘玉华等[6]通过改良座滴法研究了Ag-Cu-Ti/ZrO2陶瓷体系的润湿行为和界面特征,得到不同Ti含量的Ag-Cu-Ti合金在ZrO2陶瓷基板上的润湿性及其界面微观结构的影响规律.刘兰霄[7]通过改良静滴法观察了1 773~1 873 K的温度范围内熔融Ni-(Cr,W)合金在单晶与多晶Al2O3基板上的润湿行为.有色冶金的成分复杂,烟气温度高,其中除了固态粉尘,可能还夹杂熔化的低熔点金属,固态粉尘将在过滤管表面堆积形成滤饼[8-9].熔化金属可能在陶瓷管与滤饼之间产生黏接作用并堵塞陶瓷管微孔,影响反冲洗的效果,进而影响除尘器的使用寿命.可见有色冶金中的低熔点金属与刚玉陶瓷过滤管之间的润湿作用是一个值得研究的内容.
本论文使用的刚玉微孔陶瓷过滤管是自行设计并制备的.把碳化硅、氧化铝、碳粉等原料进行预烧结,粉碎成颗粒后过筛得到不同颗粒等级的骨料,加入造孔剂和黏结剂,再经过热压成型工艺烧制得到孔隙特性分布均一的管状刚玉微孔陶瓷过滤膜,其中孔径约为39 μm,骨架密度为2.8~3.7 g/cm3.采用压汞法对研制的陶瓷管膜进行孔隙率的测定,采用自行研制的三相界面测定仪研究锡在陶瓷管膜表面的润湿性并依据图像处理技术和理论计算,提出一种测量多孔表面液滴渗透速度的方法[10],推导出液滴向陶瓷管微孔内渗透的速度方程.
1 微孔陶瓷管孔隙率的测定孔隙率是多孔材料的关键指标,是影响多孔材料若干性能最主要的因素.刘颀等[11]采用质量体积法、浸泡介质法和压汞法3种实验方法测定了多孔石墨材料的孔隙率,并对测定结果进行比较分析.刘玫潭等[12]采用阿基米德法、质量体积法和压汞仪法测试了SiC预制件的孔隙率,并对测试结果进行比较分析.压汞法以及气体(氮气)吸附法是研究孔隙结构常用的方法,可以有效地研究孔隙大小、形态以及结构特征.压汞法具有测量速度快、对样品的形状要求不高、测量范围大等特点;低温氮气吸附法测试的最小孔径为0.6 nm,最大孔径为100~150 nm,与压汞法相比,低温氮气吸附法对小孔径的测试准确,但受样品形状影响较大.2种方法各有特点,测量孔径范围也不相同,在实际测试中往往是结合多种方法进行综合分析的.另外,也可以通过光学显微镜和扫描电镜直接观察孔隙的结构特征.
本文研究的刚玉陶瓷管孔径大致在10~100 μm范围内,属于大孔,超出了液氮吸附法的测量范围.而且表面形貌崎岖,存在大量颗粒、凹坑、孔洞、沟槽,采用高精度光学显微镜难以找到一个平面来清晰地显示其表面形貌,在图像处理时也很难从模糊的图片中分辨出何为有效孔隙,故采用水银压入法测量其孔径分布.
1.1 实验原料与实验方法陶瓷管作为一种多孔过滤介质,其孔隙特性是其最重要的性质,其中孔径大小、孔隙分布直接影响其过滤效果及使用价值.随机取热压成型的5段陶瓷管膜,通过压汞法测量其孔隙分布,每段均为长度约70 mm,外径约62 mm,内径约42 mm,壁层厚度约10 mm的短管.
实验中采用压汞法测量孔隙率,使用清华大学Autopore IV-9500全自动压汞仪,测试孔径范围为3 nm~360 μm.水银压入法[13-14]首先由里特(H. L. Ritter)和德列克(L. C. Drake)提出.它是基于水银对大多数固体表面具有的不可润湿性质,在真空条件下将汞注入样品管中,然后将样品管放入高压站进行分析.水银在不断增加的压力作用下被挤入多孔材料的孔隙中,通过施加的压力大小和材料孔径的大小之间的模型计算来求得多孔介质材料的孔径分布.
假设多孔材料的孔隙是一系列垂直于材料表面大小不同的圆柱状毛细管,根据毛细管内液体升降原理,水银所受压力P和毛细管半径r的关系是:
| $ r=\frac{2\sigma \cos \theta }{P} $ | (1) |
式(1)中:r为毛细管半径,nm;σ为水银的表面张力,N/m;25 ℃时为0.4842 N/m,50 ℃时为0.472 N/m;θ为所测多孔材料与水银的接触角,在135°~142°范围内;P为水银的外驱压力,N/m2.
根据施加压力P随时间的曲线,结合水银压入量随时间的变化,便可求出材料不同大小的微孔所占的体积,进而得到多孔材料的孔径分布.本实验所用压汞仪可直接得到孔径大小以及孔径分布数据.
1.2 陶瓷管的孔隙分布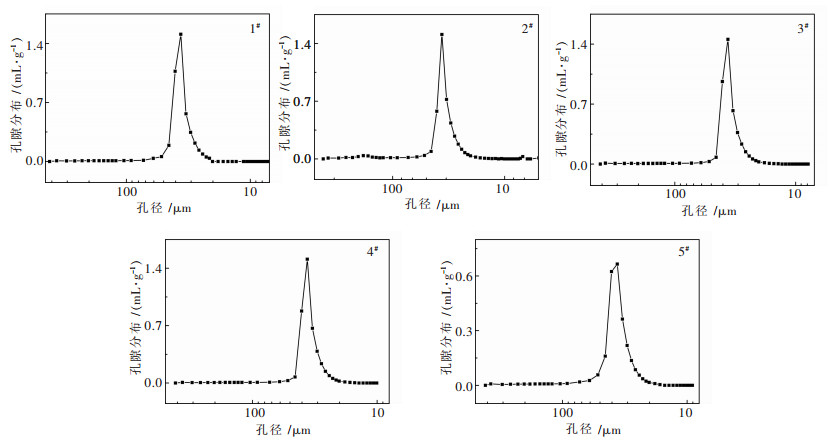 |
| 图 1 陶瓷管样品的孔隙分布 |
| 表1 陶瓷管试样的内径与外径 |
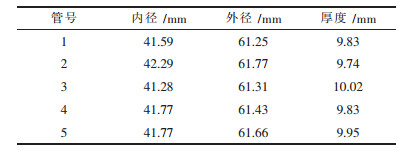 |
| 点击放大 |
5段陶瓷管样品的尺寸基本一致,内径均在42.0±0.5 mm范围内,外径在62.0±1.0 mm范围内,管壁厚度在10.0±0.3 mm范围内.
对5段陶瓷管样品分别进行压汞处理,得到其孔径分布如图 1所示.五段陶瓷管的孔径分布比较集中,基本都处于20~50 μm的范围内,达到了预期的设计,可见陶瓷管将有良好而稳定的过滤效果.
如表 2所示,5段陶瓷管样品的中孔孔径(体积)非常接近,为38~39 μm左右,孔隙度也比较接近且都大于30 %,平均孔径差别略大,但是也集中于33~39 μm的范围内.对陶瓷管做EDS和XRD分析,结合陶瓷管热压成形的工艺设计,知道陶瓷管的主要成分为α-Al2O3(刚玉)和少量SiC,同时还夹杂了造孔剂和烧结剂成分.刚玉的密度为3.965 g/cm3,致密SiC的密度为3.22 g/cm3,因此陶瓷管的骨架密度应在两者之间.1号、2号、5号陶瓷管样品的密度符合这一推断,但是3号、4号管的骨架密度却超出了这个范围,而且孔隙度也明显较低,这是由于SiC和刚玉分布不均而导致的,推测3号、4号管中游离C和SiC的含量比另外3根管更高.另外XRD分析中除了刚玉相的峰值外,其他物质都不明显,说明晶型有比较大的缺陷.由此看出,陶瓷管的造孔结果比较好,孔隙分布整体比较均匀,但是物料分布并不理想.
| 表2 陶瓷管分段的压汞测量结果 |
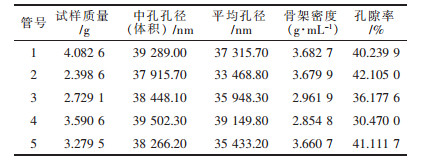 |
| 点击放大 |
2 锡在刚玉陶瓷管上的润湿现象 2.1 实验装置与流程
使用实验室自行研制的的三相界面测定仪,此装置主要包括真空系统、加热系统、成像系统和图形处理计算.
真空系统是由机械泵的真空机组来实现.为保证实验中的氧分压,实验中向炉内通入高纯氩气+5 %H2(体积分数)(Po2≤10-6 MPa,流量0.2 mL/min,压力0.1 MPa)的混合保护气,多次抽真空并加入微米钛粉作为氧化剂吸氧.高温管式炉为主要的加热设备,成像系统由Nikon-D90数码相机和100 mm长焦距镜头组成.图形处理计算系统主要包括计算机及相应的计算软件.成像系统拍摄的熔化样品图片通过图像软件处理得到二值图,然后再用软件模拟得到数据.利用Dropmeter软件[15]测量两相间的平衡接触角、前接触角、后接触角以及熔滴的体积和表面张力.
2.2 接触角模型对于液相体积不发生变化的金属/陶瓷体系来说,润湿性一般用接触角来衡量.基于固体表面特性,平衡接触角的表征有3种方法,即Young’s方程、Wenzel模型和Cassie模型.
| $ 杨氏方程为:\ \ \ \ \ \ {{\gamma }_{\text{sv}}}-{{\gamma }_{\text{SL}}}={{\gamma }_{\text{Lv}}}\cos \theta $ | (2) |
式(2)中,γsv为固气界面自由能,γSL为固液界面自由能,γLv为气液界面自由能,θ为接触角.该方程适用于均匀表面和固液间无特殊作用的平衡状态.
当固体表面是成分均一的粗糙表面时,Wenzel模型认为表面的微观凸起使得实际固液两相接触面积大于表观的几何面积,因而增强了疏水性(或亲水性).模型假设液相始终填满固体表面的凹陷结构,从热力学角度可以得到适合任何复合表面的接触角方程:
| $ \cos {{\theta }^{*}}={{f}_{1}}\cos {{\theta }_{1}}+{{f}_{2}}\cos {{\theta }_{2}} $ | (3) |
式(3)中,f1、f2为气液两相分别在固体表面上所占比例(f1+f2=1),θ1、θ2为两相与固体表面之间的本征接触角,θ*为液相在粗糙表面上的表观接触角.
Cassie模型则认为液滴在粗糙表面上的接触是一种复合接触,粗燥表面上的液滴没有填满表面上的凹槽孔隙,孔隙中填充着气相,因而可以认为液相与固相的接触面积比表观面积要小,表观上的两相接触是由固液、固气接触共同组成.从热力学角度考虑,平衡时,粗糙表面的表观接触角θ*是本征接触角θe和气液接触角180°的平均值,即:
| $ \cos {{\theta }^{*}}={{f}_{\text{s}}}\left( 1+\cos {{\theta }_{\text{e}}} \right)-1 $ | (4) |
式(4)中:fs为固相粗糙面中实际接触面积Ss与表观测量面积Sp之比(fs < 1).
当固体表面是成分均一的粗糙表面时,Wenzel模型认为表面的微观凸起使实际固液两相接触面积大于表观的几何面积.Cassie模型则认为液滴在粗糙表面上的接触是一种复合接触,粗糙表面上的液滴没有填满表面上的凹槽孔隙,孔隙中填充着气相,因而可以认为液相与固相的接触面积比表观面积要小,表观上的两相接触是由固液、固气接触共同组成.
2.3 锡在多孔陶瓷切片平面的润湿现象锡的熔点为231.98 ℃,作为常见的低熔点金属[16],锡存在于有色冶金的烟气中,并且可以处于融化状态.选取锡作为低熔点金属的代表,测定锡与刚玉陶瓷管膜之间的润湿性,为刚玉微孔陶瓷管在有色烟气中的应用进行基础理论研究.锡由高温熔炼炉熔炼所得高纯锡粉(>99 %)冷凝而成,之后磨去表面氧化膜,经超声清洗,以降低氧化对润湿的影响.采用实验室研发的三相界面测定仪,取陶瓷管膜切片,在切片的水平表面放置质量大约为0.6 g的圆柱状金属锡.升温至240 ℃,锡融化,观察其融化过程,融化完成后保温1 h,确定锡与多孔陶瓷表面的润湿达到平衡.保温完成后取出样品,检测锡的渗入情况,以评价实际生产中熔融低温金属对陶瓷管膜的堵塞情况.锡先从底面的圆周开始熔化,之后整体熔化,最终经形变并不明显的收缩过程达到稳定.熔融锡在陶瓷管表面形成了典型的球形液滴,两者之间的接触角大于90 °,熔融锡与刚玉微孔陶瓷管的表观润湿性较差.
采用图像学方法处理熔融锡照片,并拟合求解其表面张力和表观接触角[17],得到:在240℃下,熔融锡在刚玉陶瓷管切片上的体积为8.76×10-2cm3,表观接触角为160.98 °,表观计算表面张力为343 mN/m.遵循同样的实验流程进行对比实验,计算锡在刚玉基板上的接触角,即为锡和刚玉的真实接触角,得到:在240 ℃下,熔融锡在刚玉基板上的体积为8.374×10-2cm3,表观接触角为127.82°,表面张力为495 mN/m.
锡与陶瓷管和刚玉板的结合较差,降温后直接脱落,推测两者之间的润湿属于Cassie模型或Cassie-Baxter模型的应用范围.通过表观接触角和真实接触角的值,依据Cassie模型计算得到实验中使用的陶瓷管表面孔隙率为85.89 %.使用Wenzel模型计算得到的孔隙率大于1,可见Wenzel模型并不适用于锡和刚玉多孔陶瓷管之间的润湿.
为了进一步确定适用于两者间润湿现象的模型,对熔融后的试样冷却到常温后进行了SEM和EDS检测.图 2为融化分离后锡与陶瓷管接触面以上的锡的SEM图像.从图 2可看出,Sn表面比较平整,零散分布着一些凹坑,其中大多数凹坑的大小不超过100 μm,少数凹坑达到了100 μm,这也与陶瓷膜表面颗粒的大小比较符合.
 |
| 图 2 熔锡与陶瓷管膜接触面以上锡的形貌 |
锡在240 ℃条件下与刚玉陶瓷过滤管之间的润湿性很差,符合Cassie模型.为了确定锡在更高的温度下与陶瓷管膜之间的润湿性是否会发生改变,进行了升温实验.利用三相界面测定仪,在240 ℃以上每升高100 ℃对熔锡保温1 h,拍照并对图像进行处理,拟合求解锡在240~640 ℃温度范围内与陶瓷过滤管之间的润湿性.
图 3展示了不同温度下锡与陶瓷管膜之间的表观接触角和表面张力.锡与陶瓷管之间的表观接触角随着温度的升高而有所波动,但是均大于150 °,两者之间润湿性没有得到改善.因此,认为在240~640 ℃范围内,两者之间的润湿依然符合Cassie模型.
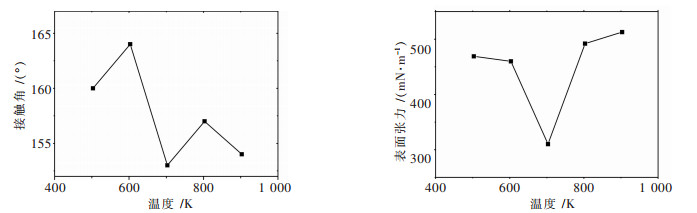 |
| 图 3 不同温度下锡与陶瓷管膜之间的表观接触角和表面张力 |
3 陶瓷膜的渗透速度 3.1 理论推导
锡与刚玉陶瓷管膜之间的润湿性很差,且符合Cassie模型.根据多孔表面模型分析知道粗糙的表面有使亲者更亲、疏者更疏的倾向.即刚玉本身与熔锡的润湿性差,刚玉陶瓷管与熔锡的润湿性则更差.
有色金属烟气中除了含有熔融的低熔点金属以外,还有水和有机油等油性存在.但是与陶瓷管接触后,可能由于压力和温度的关系而液化,于是主要研究水和油类在陶瓷管表面的润湿情况.
采用单反相机拍摄记录水滴和油滴在陶瓷管表面的入渗过程,假设液滴在入渗过程中其外形为椭球形,通过相机图像读出其轮廓的几个特征长度,问题便变为求一个圆柱体平切一个椭球的体积问题.
如图 4所示,液滴的体积可以分为2个部分:
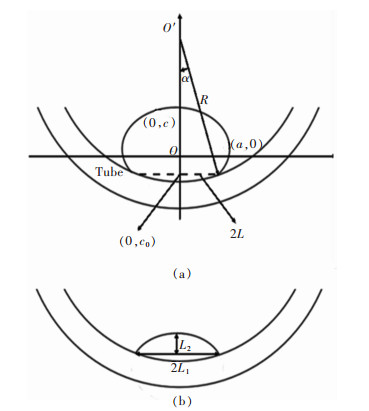 |
| 图 4 在管内面的液滴形状尺寸图(a)和管内面的接触角小于90°的液滴形状(b) |
| $ {{V}_{\text{droplet}}}={{V}_{\text{ellipsoid}}}+{{V}_{\text{tube}}} $ | (5) |
式(5)中Vellipsoid表示连接液滴与管壁左右接触点的虚线的上部分椭圆的体积,Vtube表示虚线下部分夹在管壁之间的体积.Vdroplet是液滴的体积.从图 4中读出了椭球的3个特征长度,椭球的方程可以写成:
| $ \frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}+\frac{{{z}^{2}}}{{{c}^{2}}}=1 $ | (6) |
| $ \frac{{{x}^{2}}}{{{a}^{2}}\left( 1-\frac{{{z}^{2}}}{{{c}^{2}}} \right)}+\frac{{{y}^{2}}}{{{b}^{2}}\left( 1-\frac{{{z}^{2}}}{{{c}^{2}}} \right)}=1 $ | (7) |
根据式(6)和式(7)确定椭球方程和三相接触点的位置以后,Vellipsoid由式(8)表示:
| $ {{V}_{\text{ellipsoid}}}=\int_{{{c}_{0}}}^{c}{\text{ }\!\!\pi\!\!\text{ }ab\left( 1-\frac{{{z}^{2}}}{{{c}^{2}}} \right)\text{dz}} $ | (8) |
对式(8)求积分得到式(9):
| $ {{V}_{\text{ellipsoid}}}=\text{ }\!\!\pi\!\!\text{ }ab\left[\left( c-{{c}_{0}} \right)-\frac{1}{3{{c}^{2}}}\left( {{c}^{3}}-c_{0}^{3} \right) \right] $ | (9) |
接下来求解Vtube.Vtube实际上沿着垂直z轴方向的切面形状是一系列被两条平行线夹住的椭圆的部分,理论上可以写出积分形式,但是实际发现无法求出解析解,因此这里做一个近似假设,假设这一系列切面均为长方形,于是Vtube可以表示为:
| $ {{V}_{\text{tube}}}=4b\int_{{{c}_{0}}-R\left( 1-\cos \alpha \right)}^{{{c}_{0}}}{x\text{d}z=4b}\int_{\pi /2-\alpha }^{\pi /2}{{{R}^{2}}{{\cos }^{2}}\varphi \cdot \text{d}\varphi } $ | (10) |
| $ \sin \alpha =l/R $ | (11) |
式(10)和式(11)中,R为陶瓷管的内半径.
最终可以求得液滴体积:
| $ {{V}_{\text{droplet}}}=\text{ }\!\!\pi\!\!\text{ }ab\left[\left( c-{{c}_{0}} \right)-\frac{1}{3{{c}^{2}}}\left( {{c}^{3}}-c_{0}^{3} \right) \right]+4b{{R}^{2}}\left( \frac{\alpha }{2}-\frac{\sin 2\alpha }{4} \right) $ | (12) |
对于液滴在平板上的体积,只需要除去Vtube项即可.而对于液滴在陶瓷管凸面一侧的情况,Vellipsoid和Vtube由相加变为相减,得到液滴体积如下:
| $ {{V}_{\text{droplet}}}=\text{ }\text{ }\!\!\pi\!\!\text{ }\text{ }ab\left[ \left( c-{{c}_{0}} \right)-\frac{1}{3{{c}^{2}}}\left( {{c}^{3}}-c_{0}^{3} \right) \right]-4b{{R}^{2}}\left( \frac{\alpha }{2}-\frac{\sin 2\alpha }{4} \right) $ | (13) |
图 4(a)是液滴在管内壁表观接触角大于90 °时的形貌,从拍摄的照片中直接测量椭圆参数a、b的值,但是当液滴开始向管内渗透后,其表观接触角处于小于90 °的状态.如图 4(b),需利用数值拟合方法得到液滴轮廓的数学描述,对于这种情况采用球体近似,认为表观接触角小于90 °时液体的轮廓为一段球弧面.由于圆球也是椭球的一种,所以只需求得球体的半径r,即可用式(12)和式(13)求得液体体积,对于球体而言a=b=c=r,由图 4(b)可以看出,只需从图 4中量出L1、L2即可求出球弧面的半径r,由式(14)表示:
| $ r=\left( L_{1}^{2}+L_{2}^{2} \right)/2{{L}_{2}} $ | (14) |
| $ {{V}_{\text{droplet}}}=\text{ }\!\!\pi\!\!\text{ }\left( \frac{L_{1}^{2}{{L}_{2}}}{2}+\frac{L_{2}^{3}}{6} \right)+4rR\left( \frac{\alpha }{2}-\frac{\sin 2\alpha }{4} \right) $ | (15) |
式(15)为液滴在管内壁表观接触角小于90 °时液滴体积的计算公式.
3.2 实验结果选取一段陶瓷管试样,测量其内半径为20.88 mm,外半径为30.83 mm,管壁厚度9.95 mm,代入上述体积公式计算出液滴体积变化量,然后根据拍照所得的渗透时间,可计算液滴在多孔陶瓷管上的渗透速度.由于水在陶瓷管上渗透速度快,采用与陶瓷管润湿性良好但是黏度更大的油进行实验,实验中使用的油为ULVAC公司生产的SMR-100型真空泵油,种类为矿物油,密度0.878g/cm3(15 ℃),闪点低于200 ℃,运动黏度44.6 mm2/s(40 ℃).采样设备为佳能EOS600D相机,长变焦镜头,最近距离为0.25 m,拍摄帧率25次/s.
图 5示出液滴在多孔陶瓷管内表面上的渗入过程及第一秒的体积变化,取像间隔时间为3帧(0.12 s).逐帧观察液体渗透的过程,发现液滴首先在陶瓷管表面铺展并同时渗入,铺展到一定程度后铺展范围基本保持不变并继续渗入孔隙,最后铺展范围缓慢缩小,直至液滴完全渗入.液滴入渗过程逐渐变慢是因为液滴入渗的2个驱动力(重力与毛细管力)中的重力随着液滴不断渗入逐渐变小;可以看出液滴体积在10帧以内明显的下降,减少40 %,之后体积变化不大,达到稳定状态.即液滴开始快速渗入陶瓷管并且铺展,之后的渗入速度明显下降.
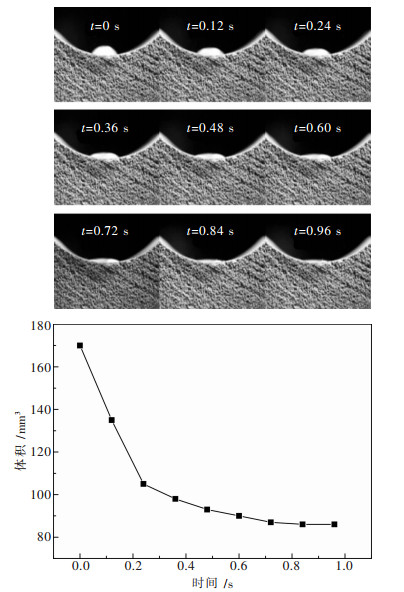 |
| 图 5 液滴入渗过程示意图及渗入过程中的液滴体积变化 |
4 结论
1)采用压汞法测量微孔陶瓷管孔隙率,对五段陶瓷管样品分别进行处理,测量得到五段陶瓷管的大小基本一致,孔径分布比较集中,中孔孔径(体积)非常接近,为38~39μm,孔隙度也比较接近且都大于30%.
2)测量了锡与陶瓷管膜在240~640 ℃范围内的表观润湿现象.锡与陶瓷管膜的接触角在实验温度范围内均大于150 °,随温度升高,两者间的表观接触角和表面张力有一定波动.在高温下保温一段时间锡也没有完全渗入陶瓷管的微孔,并且容易剥离.
3)锡与刚玉陶瓷管膜的润湿性很差,适用于Cassie模型,表明陶瓷过滤管膜实际使用时,锡将附在管膜表面,不会堵塞孔道,易在反冲洗时脱离.
4)根据图像处理技术和理论计算,提出一种测量多孔表面液滴渗透速度的方法,得到液滴在刚玉陶瓷管膜上的渗透速度公式.
5)以油滴进行试验,发现渗透过程中液滴首先会进行铺展,并且一段时间内维持其铺展半径直至最终完全渗入.油滴在渗入孔隙的过程中入渗速度有大幅降低,在前0.5 s内快速入渗并且铺展,之后的渗入速度降低缓慢.
| [1] | 袁章福, 吴燕, 徐红艳, 等. 冶金烟气微孔陶瓷管膜研制及深度除尘应用的研究[J]. 有色金属科学与工程, 2014, 5(3): 1–8. |
| [2] |
Kumar G, Prabhu K N. Review of non-reactive and reactive wetting of liquids on surfaces[J].
Advances in Colloid and Interface Science, 2007, 133(2): 61–69. DOI: 10.1016/j.cis.2007.04.009. |
| [3] | Starov V M, Velarde M G, Radke C J. Wetting and spreading dynamics[M]. Boca Raton: CRC press , 2007. |
| [4] | 陈名海, 刘宁, 许育东. 金属/陶瓷润湿性的研究现状[J]. 硬质合金, 2002, 19(4): 199–205. |
| [5] | 杨龙龙.稀土La、Ce与陶瓷的润湿性及界面结构[D].吉林:吉林大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10183-1012367573.htm |
| [6] | 刘玉华, 庄宇, 胡建东, 等. Ag-Cu-Ti合金与ZrO2陶瓷的润湿性及界面特征[J]. 电子显微学报, 2014, 33(1): 34–39. |
| [7] | 刘兰霄.熔融Ni-(Cr, W)合金与Al2O3陶瓷的润湿性研究[D].重庆:重庆理工大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11660-2010031668.htm |
| [8] | 林庚, 倪文, 陈德平, 等. 陶瓷无机膜过滤除尘器的高温除尘机理研究[J]. 中国矿业, 2007, 16(1): 105–107. |
| [9] | 王哲, 任凤章, 李锋军, 等. Fe2O3对SiC基泡沫陶瓷过滤器性能的影响[J]. 材料热处理学报, 2008, 29(1): 20–23. |
| [10] | 袁章福, 吴燕, 徐红艳, 等.一种图像法测量微孔材料渗透性能的方法:中国, CN201410305569.9[P].2014-07-01. |
| [11] | 刘颀, 胡亚非, 熊建军. 石墨多孔材料孔隙率测定方法研究[J]. 润滑与密封, 2010, 35(10): 99–101. |
| [12] | 刘玫潭, 蔡旭升, 何丽娇, 等. 造孔剂含量对多孔SiC预制件孔隙率的影响及孔隙率测定方法探究[J]. 材料导报, 2013, 27(7): 108–112. |
| [13] | 陈悦, 李东旭. 压汞法测定材料孔结构的误差分析[J]. 硅酸盐通报, 2006, 25(4): 198–201. |
| [14] | 王红梅. 压汞法测定多孔材料孔结构的误差[J]. 广州化工, 2009, 37(1): 109–111. |
| [15] |
Xu B, Yuan Z, Wu Y. Simulation analysis on surface morphology and hysteresis characteristics of molten Sn-3.0Ag-0.5Cu sitting on the inclined Ni substrate[J].
Colloids and Surfaces A, 2014, 441(1): 217–225. |
| [16] |
Yuan Z, Mukai K, Takaki K, et al. Surface tension and its temperature of molten tin determined with the sessile drop method at different oxygen partial pressure[J].
Journal of Colloid and Interface Science, 2002, 254(2): 338–345. DOI: 10.1006/jcis.2002.8589. |
| [17] | 袁章福, 柯家骏, 李晶. 金属及合金的表面张力[M]. 北京: 科学出版社 , 2006. |
 2014, Vol. 5
2014, Vol. 5


