| 砂岩单轴压缩变形规律及声发射特性 |
2. 江西荡坪钨业有限公司, 江西 大余 341514
2. Jiangxi Dangping Tungsten Industry Co., Ltd, Dayu 341514, China
岩石的非均匀性使其受荷载过程中应力分布不稳定,产生局部应力集中,达到高能状态. 这种状态并不稳定,通过产生瞬态弹性波并向周围传播,以此快速释放能量而达到稳定状态的现象称为声发射(Acoustic Emission,简称AE). 目前,声发射试验研究已取得丰硕的成果,其成果可概括为以下几类:①分析材料AE特性,以反演的分析方法,推测材料破坏的类型,对其损伤状态作出合理评判[1-6];②判断声发射源的位置及产生机制[7-9];③捕获并研究岩石的失稳前兆AE信息,提出相关合理的岩石破坏前兆判据[10-14].
由于矿山地下开采使原岩应力重新分布,导致局部应力集中,脆性岩石容易发生岩爆,这是严重的安全隐患. 因此,准确预测预报岩爆对于矿山安全开采具有重大意义.
1 砂岩单轴压缩试验 1.1 试验设备及材料试验材料取自某钨矿砂岩,试件尺寸为Ф50 mm,高度100 mm. 试件端面不平行度小于0.02 mm,以消除加载过程中由于端面不平产生的AE干扰信号,并且试件侧面打磨出一个宽度与传感器直径大致相同的面,用于良好接触声发射传感器,这样能更有效地接收岩石破坏产生的AE信号. 试验是由RMT-150C加载系统和SAEU2S声发射检测系统组成,见图 1、图 2.
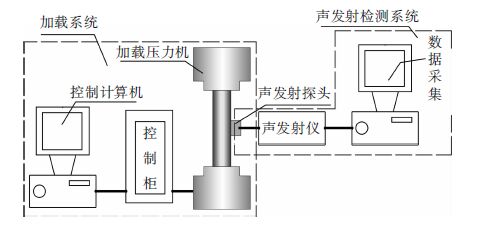 |
| 图 1 室内声发射试验系统框图 |
 |
| (a)加载系统,(b)声发射探头布置,(c)声发射检测系统 图 2 试验系统 |
1.2 试验参数设置及操作
试验控制模式:力-行程,速率为0.2 kN/s;声发射传感器为谐振SR150M 型,中心频率60~400 kHz,固定在岩样侧部打磨面中心,设置AE系统波形门限43 dB、参数门限43 dB、前放增益43 dB、采样频率800 kHz、采样长度2 048、参数间隔2 000 μs、滤波器100~400 kHz.
在试件2个端面和传感器接触处都涂黄油耦合,传感器贴在试件侧面中央,用胶带和胶水固定. 试件处理安装完成后,按以上参数设置好声发射检测系统参数,试验开始前在岩样侧面进行断铅测试,检验探头的灵敏度以及探头与岩样的耦合度. 试验时保持两系统时间和操作同步.
2 试验结果与分析 2.1 岩石破坏形态试验砂岩试件达到强度的85 %~90 %时,试样表面出现宏观裂隙,继续加载,裂隙扩张,局部岩石片落崩飞,岩块破坏前轴向位移较小. 破坏时发生爆裂声,振动较大,主要形成2种大小的岩块,块度小岩块较破碎,并且部分岩片弹射较远,块度大的较完整,见图 3.
 |
| 图 3 岩石破坏形态 |
2.2 岩石应变分析
图 4为此试验典型荷载-位移全变化关系曲线. 试验岩样破坏前轴向应变较小,峰值应力后岩样瞬间破坏,发生岩爆,形变时间极短. 其破坏过程可分为以下几个阶段:
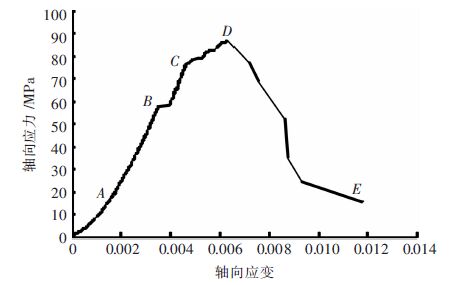 |
| 图 4 应力-应变关系曲线 |
(1)OA段:对应σc的0~20.3 %. O点为曲线起始点,荷载-位移曲线上凹,该线段的斜率由小变大,变形速率减缓,表明岩块内原有裂隙在加载过程中逐渐闭合,荷载增加速率一定时,闭合速率逐渐减小. 此阶段为压密阶段,岩块体积减小,A点应力称为压密极限.
(2)AB段:对应σc的20.3 %~66.8 %. 此线段荷载-位移曲线保持线性关系,岩块变形速率基本保持一定,为弹性变形阶段,B为弹性极限.
(3)BC段:对应σc的66.8 %~86.4 %. B点位移急速加快,为曲线拐点. 此阶段为屈服阶段,C点为屈服极限,岩块微裂纹开始扩展,稍有“扩容”现象.
(4)CD段:对应σc的86.4 %~100 %. 岩样中的裂隙扩展迅速且不稳定,局部有岩块弹射、崩落、抛出,显示出宏观破坏迹象,随着荷载加大,扩容加速,裂纹扩展贯通形成滑动面. 此阶段为破坏阶段,σc值为D点对应应力值.
(5)DE段:时间极短,未能采集到AE信息,为破坏后阶段. 峰值荷载D点时,岩样失稳破坏.
2.3 岩块声发射参数分析压密阶段和线弹性阶段AE振铃计数较少,累积能量曲线十分平缓,释放弹性应变能较低,主要原因是由于多数原生微裂隙压实和少量微破裂的产生引起. 屈服阶段AE活动有逐渐增加的趋势,岩块释放的弹性能逐渐增大. 主要原因是由于大量的微裂纹开始形核、成核,最后微裂纹稳定扩展所产生. 破坏阶段振铃计数值较前3个阶段大,且更密集,AE类型多为连续型,偶尔有突发峰值,这是因为有新宏观裂隙形成. 累积能量的阶跃对应AE振铃计数峰值. D点时,振铃计数与累积能量都达到最大值,较前3阶段峰值大10倍以上. 时间-应变关系曲线拐点处,AE活动较集中,由B点和CD阶段可看出. 破坏阶段曲线拐点多,振铃计数密集,AE活动活跃,AE累积能量急剧增加,达到105量级,这是明显的破坏前兆,峰值应力时AE累积能量达到106数量级,振铃计数也达到最大值,见图 5、图 6.
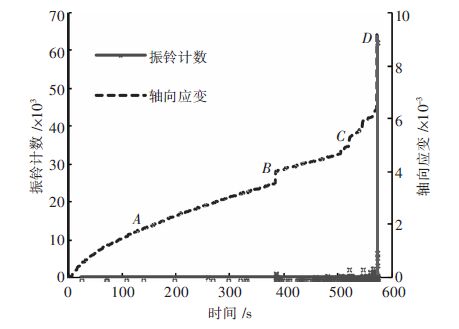 |
| 图 5 振铃计数-时间-应变关系曲线 |
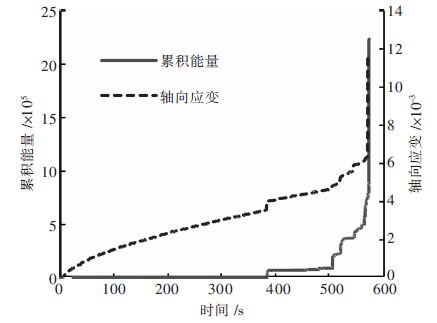 |
| 图 6 累积能量-时间-应变关系曲线 |
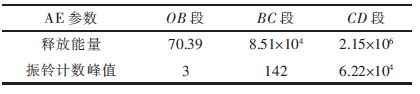
对加载过程的各阶段的释放能量和振铃计数峰值进行统计,如表 1所示。CD阶段所释放的能量为OC阶段所释放能量的25.24倍,振铃计数峰值为OC阶段的429倍. 由此可知,砂岩单轴压缩条件下,破坏前的振铃计数和释放能量较小,增长平缓,到临近峰值应力时,声发射参数急剧增加,岩块内能量加速释放,峰值应力瞬间破坏,AE参数达到最大值,峰值应力后几乎采集不到AE参数,为典型的脆性破坏,具有较强的岩爆倾向性.
| 表1 各阶段释放能量和振铃计数峰值 |
 |
| 点击放大 |
2.4 损伤分析
岩样微裂纹的演化是一种随机变化的过程. 因此,可采用非平衡统计岩石破坏的过程分析. 假定微单元强度服从威布尔密度分布函数[15-18]:
| $\varphi \left( \varepsilon \right) = {m \over \alpha }{\varepsilon ^{m - 1}}\exp \left( { - {{{\varepsilon ^m}} \over \alpha }} \right)$ | (1) |
式(1)中:ε为岩样应变值;m为-形状参数;$\alpha $为尺度参数;$\varphi \left( \varepsilon \right)$为微元损伤率.
假设损伤量为D,所以,可以用以下公式表示损伤量与微元损伤率的关系:
| ${{dD} \over {d\varepsilon }}\varphi \left( \varepsilon \right)$ | (2) |
联合式(1)和式(2),可得:
| $D = \int_0^\varepsilon {\varphi \left( x \right)} dx = 1 - \exp \left( { - {{{\varepsilon ^m}} \over \alpha }} \right)$ | (3) |
AE振铃计数能够反映岩样内部AE活动规律,从而能够反映岩样内部裂纹等缺陷的发展规律,因此能够反映试件的损伤情况. 假设为岩样破坏时的AE累积振铃计数,为应变增至ε时的积累振铃计数,则两者的关系为:
| $N = {N_m}\int_0^\varepsilon {\varphi \left( x \right)} dx$ | (4) |
由式(3)和式(4)可得:
| ${N \over {{N_m}}} = 1 - \exp \left( { - {{{\varepsilon ^m}} \over \alpha }} \right)$ | (5) |
联合式(3)和式(5),损伤D可表示为:
| ${N \over {{N_m}}} = D$ | (6) |
假设为岩样破坏时的AE累积振铃计数,t 为加载时长为t时的积累振铃计数,Dt为加载时长为t时的损伤,则有如下关系:
| ${{{N_t}} \over {{N_m}}} = {D_t}$ | (7) |
因为AE振铃计数是已知量,所以,由式(7)可绘制出岩石损伤与加载时间的关系曲线,见图 7、图 8。
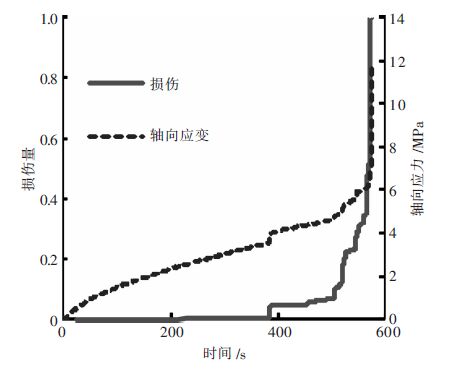 |
| 图 7 损伤-时间-应变关系曲线 |
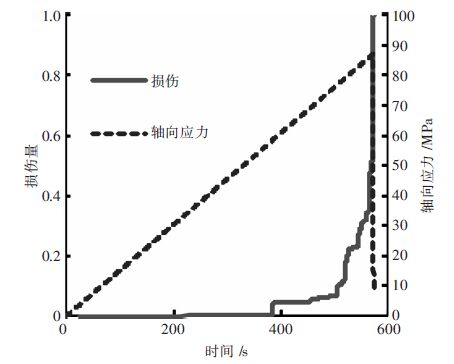 |
| 图 8 损伤-时间-应力关系曲线 |
由图 7可知,该损伤曲线变化基本上与应变曲线变化是同步的,压密、弹性阶段的损伤值极小,从塑性变形的起始点B开始,损伤值出现一个阶跃,这是比较符合实际的损伤情况,从图 8可知B点对应的应力为σc的65 %左右,损伤变量开始增大,但损伤量不及0.2,岩样还比较稳固;应力达到σc的85 %~90 %(即C点)后,岩样上出现明显的裂纹,损伤量呈阶跃增大,裂纹最终扩展贯通,发生破坏,损伤值到达1.
3 结 论(1)应力-应变关系曲线拐点处,声发射较集中,尤其是CD阶段可看出,曲线拐点多,振铃计数密集,AE活动活跃,岩样岩爆前,AE累计能量成指数级增长,破坏前兆非常显著.
(2)脆性砂岩单轴压缩过程中,AE活动在裂隙压密阶段和弹性变形阶段都不明显,到弹塑性变形阶段AE活动逐渐增加,逐渐显现宏观破坏迹象,体积膨胀加剧,局部有岩块弹射、崩落、抛出,对应AE参数峰值,应力达到峰值后岩样瞬间完全破坏. 破坏阶段振铃计数密集,且采集到信息较其他阶段大很多,声发射多为连续型. 这说明通过监测分析声发射振铃计数能够预测预报脆性砂岩岩爆破坏的发生.
(3)由AE振铃计数来表征的岩块损伤,可以真实、直观了解岩块的损伤状态. 当应力较低时,损伤量极低;塑性阶段损伤变量开始增大,但损伤量不及0.2;CD阶段,岩样上出现宏观裂隙,损伤量呈阶跃增大,最终岩样发生岩爆,损伤值到达1.
| [1] | 赵奎, 金解放, 王晓军, 等. 岩石声速与其损伤及声发射关系研究[J]. 岩土力学, 2007, 28(10): 2105–2109. |
| [2] | 刘保县, 黄敬林, 王泽云, 等. 单轴压缩煤岩损伤演化及声发射特性研究[J]. 岩石力学与工程学报, 2009, 28(s1): 3231–3234. |
| [3] | 赵奎, 钟赣平, 谢良. 声波透射法分析桩身混凝土质量的相对强弱指标法[J]. 有色金属科学与工程, 2011, 2(2): 52–56. |
| [4] | 徐小丽, 高峰, 季明. 温度作用下花岗岩断裂行为损伤力学分析[J]. 武汉理工大学学报, 2010, 32(1): 143–147. |
| [5] |
Dai S T, Labuz J F. Damage and failure analysis of brittle materials by acoustic emission[J].
Rock Mechanics and Rock Engineering, 2005, 38(1): 1–19. DOI: 10.1007/s00603-004-0031-6. |
| [6] | 金解放, 钟海兵, 吴越, 等. 静载荷与循环冲击作用下岩石损伤变量定义方法的选择[J]. 有色金属科学与工程, 2013, 4(4): 85–90. |
| [7] | 康玉梅, 朱万成, 白泉, 等. 基于小波变换时频能量分析技术的岩石声发射信号时延估计[J]. 岩石力学与工程学报, 2010, 29(5): 1010–1016. |
| [8] | 赵兴东, 李元辉, 袁瑞甫, 等. 基于声发射定位的岩石裂纹动态演化过程研究[J]. 岩石力学与工程学报, 2007, 26(5): 944–950. |
| [9] |
Manthei G. Characterization of acoustic emission sources in a rock salt specimen under triaxial compression[J].
Bulletin of the Seismological Society of America, 2005, 95(5): 1674–1700. DOI: 10.1785/0120040076. |
| [10] | 苏承东, 高保彬, 南华, 等. 不同应力路径下煤样变形破坏过程声发射特征的试验研究[J]. 岩石力学与工程学报, 2009, 28(4): 757–757. |
| [11] | 李元辉, 刘建坡, 赵兴东, 等. 岩石破裂过程中的声发射b值及分形特征研究[J]. 岩土力学, 2009, 30(9): 2559–2563. |
| [12] | 胡京涛, 赵奎, 胡慧明, 等. 尾砂胶结充填体声发射特征的分形分析[J]. 有色金属科学与工程, 2011, 2(2): 78–82. |
| [13] | 赵毅鑫, 姜耀东, 祝捷, 等. 煤岩组合体变形破坏前兆信息的试验研究[J]. 岩石力学与工程学报, 2008, 27(2): 339–346. |
| [14] |
Ganne P, Vervoort A, Wevers M. Quantification of pre-peak brittle damage correlation between acoustic emission and observed micro-fracturing[J].
International Journal of Rock Mechanics & Mining Science, 2007, 44(5): 720–729. |
| [15] | 陈忠辉, 谭国焕, 杨文柱. 岩石脆性破裂的重正化研究及数值模拟[J]. 岩土工程学报, 2002, 24(2): 183–187. |
| [16] | 唐春安, 乔河, 徐小荷, 等. 矿柱破坏过程及其声发射规律的数值模拟[J]. 煤炭学报, 1999, 24(3): 266–269. |
| [17] | 张檑. 混凝土单向受载全过程的声发射试验研究[D]. 北京:中国地质大学,2011. |
| [18] | 龚囱. 循环加卸载条件下充填体损伤与声发射特性研究[D]. 赣州:江西理工大学,2011. |
 2014, Vol. 5
2014, Vol. 5

