| 基于模糊层次分析的稀土资源储备矿种选择 |
稀土是发展高新技术不可缺少的战略资源,也是不可再生资源,随着稀土资源的不断开采,资源逐渐贫乏.如何保护稀土资源,减缓资源开采速度,是学界关注的问题,尤其是选择封存储备的矿种成为焦点.稀土资源矿种封存储备选择受多种因素影响,属于多准则决策问题,为此,引用模糊层次分析法,该方法除吸收了传统层次分析法的优点外,还在其基础上进行了改进,如针对判断矩阵构成方式和一致性检验手段进行了调整,目的是让层次分析法中较难进行的一致性检验和调整工作变得更加科学、准确和简便.
本研究利用模糊层次分析模型对稀土矿种从资源的稀缺性、功能性、前景性、矿种开采的环境危害、矿种封存涉及的补偿成本等方面构建了评价指标体系,通过定性和定量分析后做出选择判断,为相关决策部门选择储备稀土矿种提供理论依据.
1 模糊层次分析模型的构建 1.1 构建模糊一致矩阵模糊层次分析方法(以下简称为FAHP 方法)首先要构建模糊一致矩阵[1-3],模糊一致矩阵是满足以下条件的矩阵形式.
若模糊矩阵R=(rij)n×n.满足∀i, j, k
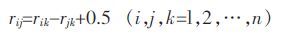
|
(1) |
则称模糊矩阵R 是模糊一致矩阵.
模糊一致矩阵必然是模糊互补的,即
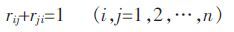
|
(2) |
因此,可以得出矩阵中对角线上元素rii=0.5.
1.2 构建模糊一致性矩阵检验FAHP 方法的一致性检验主要是基于以下2 个定理进行实现的:
定理1:模糊互补矩阵R=(rij)n×n 是模糊一致矩阵的充分必要条件是指任意指定两行的对应元素之差为常数.
定理2:模糊互补矩阵R=(rij)n×n 是模糊一致矩阵的充分必要条件是指任意指定行和其余各行对应元素之差为某一常数.
1.3 构建模糊一致性判断矩阵模糊一致判断矩阵R 表示针对上一层某元素,本层次与之有关的元素之间相对重要性的比较,设表示元素a1,a2,…,an 两两比较重要程度的模糊判断矩阵R 为

|
rij 表示元素ai 与元素aj 相对于上一层某元素进行比较时,元素ai 与元素aj 具有模糊关系“…比…重要的多”的隶属度,用0.1~0.9 标度进行度量.2 模糊层次分析模型在稀土储备矿种评价选择中的应用2.1 稀土储备矿种评价指标体系的建立在FAHP 方法中,首先要将所包含的因素分组,每一组作为一个层次,采用树形结构,按照最高层、若干有关的中间层和最低层的形式排列起来.根据稀土矿种的特性,决定将以下3 个因素设为一级指标:矿种消耗特性、矿种开采的环境特性、矿种的资源补偿特性.每个一级指标设立了相应的二级指标,如表 1 所示.
| 表1 稀土矿种评价指标体系 |
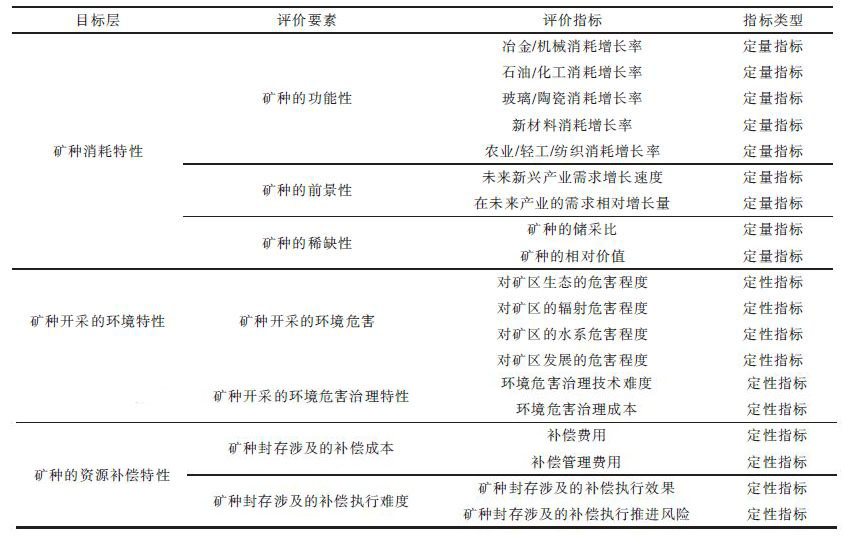 |
| 点击放大 |
2.2 模糊判断矩阵的建立及排序
构建模糊判断矩阵和层次单排序通过以下3 个步骤完成[4]:
步骤1:构建稀土矿种评价模糊判断矩阵并检验.本研究通过调研,给50 位专家发送问卷,共收回有效评分数据30 份.稀土矿种首先选择30 位专家对各指标的相对重要程度进行评价,按照前面的模糊层次分析法原理建立模糊判断矩阵,利用模糊一致矩阵的检验方法检验一致性.
根据稀土矿种评价指标体系,构建其模糊判断矩阵如下:
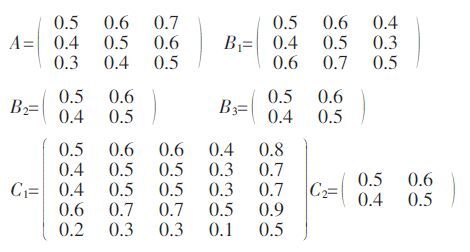
|
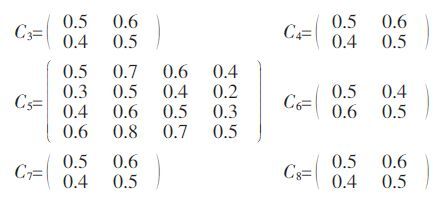
|
由于在实际问题分析和决策过程中的复杂性往往使人们在取值时会产生主观性和片面性,因此对模糊互补矩阵R 的一致性检验是有必要的.根据模糊一致矩阵的性质:模糊互补矩阵R=(rij)n×n 是模糊一致性矩阵⇔任意两行的对应元素之差相等,为同一常数.
步骤2:层次单排序.层次单排序是指,对于上一层某因素而言本层中与之有联系的因素的重要性排序.该排序可以通过公式(3)对模糊判断矩阵计算而得.
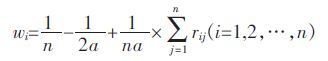
|
(3) |
其中:n 为R 的阶数,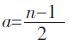
基于模糊矩阵的稀土矿种评价指标各层次排序分别如表 2 至表 12 所示.
| 表2 目标层指标排序 |
 |
| 点击放大 |
| 表3 B-A1 准则层指标排序 |
 |
| 点击放大 |
| 表4 B-A2 准则层指标排序 |
 |
| 点击放大 |
| 表5 B-A3 准则层指标排序 |
 |
| 点击放大 |
| 表6 C-B1 指标排序 |
 |
| 点击放大 |
| 表7 C-B2 指标排序 |
 |
| 点击放大 |
| 表8 C-B3 指标排序 |
 |
| 点击放大 |
| 表9 C-B4 指标排序 |
 |
| 点击放大 |
| 表10 C-B5 指标排序 |
 |
| 点击放大 |
| 表11 C-B6 指标排序 |
 |
| 点击放大 |
| 表12 C-B7 指标排序 |
 |
| 点击放大 |
步骤3:层次总排序.层次单排序得出的权重仅仅是相对于上一层元素的相对权重,最终要得到的权重是相对于总目标来说的.可以用逐层递推相乘法,假设第k-1 层的元素s 相对于总目标的权重wk-1s已经推算出来,那么第k 层的元素t 相对总目标的权重为wkt =wk-1s ·wt ,wt为层次单排序所确定的元素t 相当于上层元素s
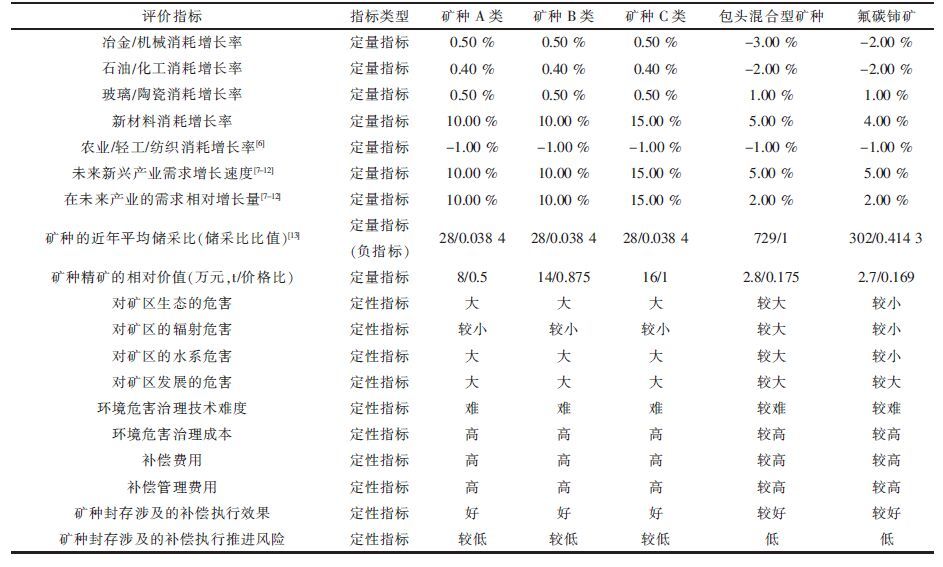
根据我国稀土矿种成矿特征以及稀土配分的不同,选择有代表性的5 类矿种,即离子吸附型稀土矿种A 类(即富镧少钇型离子矿)、离子吸附型稀土矿种B 类(即中钇富铕型离子矿)、离子吸附型稀土矿种C 类(即高钇型离子矿)、包头混合型矿种和氟碳铈矿,并对照评价指标体系收集原始数据如表 14,对原始数据进行处理便于比较.
| 表13 合成权重表 |
 |
| 点击放大 |
| 表14 稀土矿种选择评价指标体系及指标评价值 |
 |
| 点击放大 |
2.3.1 定性指标的处理
针对定性指标,由各专家代表进行打分,并按比例将分值直接控制在0~1 之间.将定性指标等级制定5 个级别,即V=[好、较好、一般、较差、差],分别对应分数为{0.9、0.7、0.5、0.3、0.1}.
2.3.2 定量指标原始数据的无量纲处理在稀土矿种评价指标体系中,各评价指标的具体性质及表现形式不同,有的是绝对指标,有的是相对指标,还有的是平均指标;有的是正指标,有的属于适度指标,还有的属于负指标,正指标则要求数值越大越好,适度指标要求数值适中为好,负指标则要求数值越小越好,因此各个指标之间不具有可比性,如果不进行无量化处理,就无法进行综合评价.
无量纲处理,就是对评价指标数值的标准化、正规化处理.它是通过一定的数学变换来消除指标量纲影响的方法,把性质、量纲各异的指标转化为可以进行综合评价的一个相对数---量化值[4].
本文中采取在量纲处理方法中被广泛采用的一种方法,即借助模糊数学中隶属函数的概念,以定量指标所使用的评分值中最大值、最小值和平均值为标准,对三类指标分别进行无量纲化处理.该方法对应两套无量纲化量化模型,正指标类模糊量化模型、负指标类模糊量化模型[1, 5].
(1)正指标类模糊量化模型.正指标类模糊量化模型用于处理正指标类数据,即该类指标对总目标的贡献率随着评价结果的增大而增大.正指标类的模糊量化模型为:

|
其中:Rj 为第j 项评价指标无量纲化处理后的评价值;xj 为第j 项评价指标的原始评分值;xjmax为对第j项评价指标评价时,采用的评分值中的最大值;xjmin 为对第j 项评价指标评价时,采用的评分值中的最小值.
(2)负指标类模糊量化模型.负指标类模糊量化模型用于处理负指标类数据,即该类指标对总目标的贡献率随着评价结果的增大而减小.负指标类的模糊量化模型为:
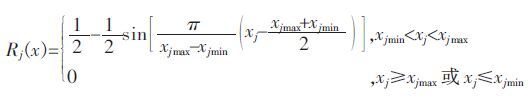
|
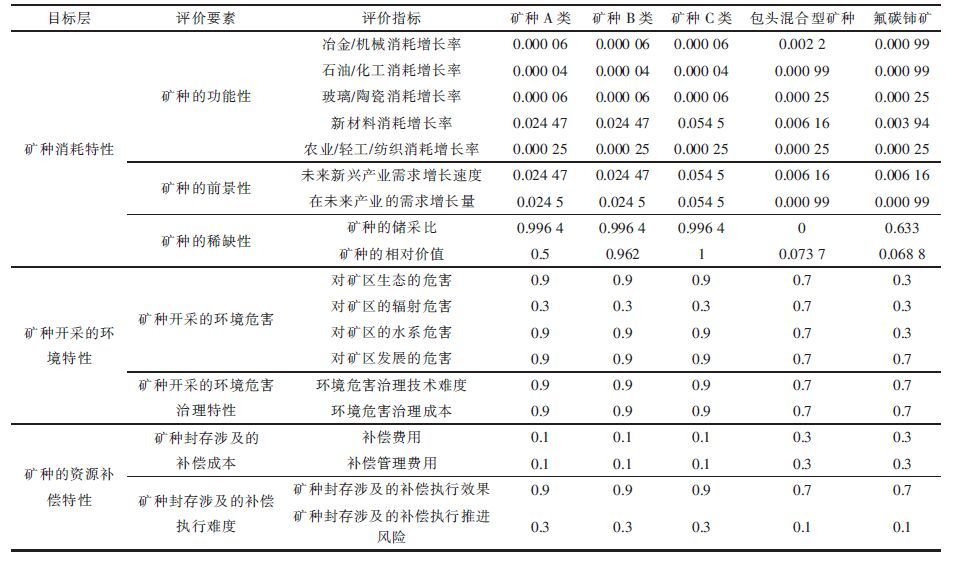
5类矿种的定性指标的评价结果以及定量指标无量纲化处理后的结果如表 15 所示.
| 表15 稀土矿种评价值 |
 |
| 点击放大 |
2.4 计算稀土矿种综合得分并进行排序分析
根据合成权重公式,可以计算得到5 种稀土矿种的综合评价结果,见表 16 所示.
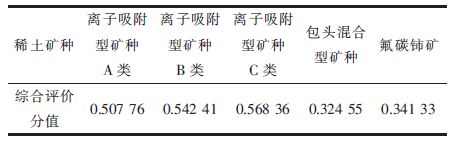
| 表16 5 种稀土矿种综合评价结果 |
 |
| 点击放大 |
3 结论
通过对影响稀土矿种储备选择的冶金/机械消耗增长率、石油/化工消耗增长率、玻璃/陶瓷消耗增长率、新材料消耗增长率、农业/轻工/纺织消耗增长率、未来新兴产业需求增长速度、矿种的储采比、矿种的相对价值等定量指标的直接赋值,以及各矿种对矿区生态的危害、矿区的辐射危害、矿区的水系危害、矿区发展的危害、环境危害治理成本、环境危害治理技术难度以及补偿管理费用等定性指标的专家打分,经过模拟计算,获得5 种矿种的综合评价分值为:离子吸附型矿种C 类综合得分为0.56836,离子吸附型矿种B 类为0.54241,离子吸附型矿种A 类为0.50776,氟碳铈矿得分为0.34133、包头混合型矿种得分为0.32455.因为稀土矿种综合评价分值越高的矿种,说明该矿种越稀缺、未来经济依赖性也越高,越要优先储备,所以,我国在稀土封存储备布局时,应该优先封存储备离子吸附型矿种C 类即高钇型离子吸附矿,其次是离子吸附型矿种B 类即中钇富铕型离子吸附矿和离子吸附型矿种A 类即富镧少钇型离子吸附矿,然后是氟碳铈矿矿种,最后是包头混合型矿种.
| [1] | 张顾海.供应链管理下的供应商选择研究[D].上海: 同济大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10285-2005135028.htm |
| [2] | 朱孔来. 评价指标的非线性无量纲模糊处理方法[J]. 系统工程, 1996(11): 58–62. |
| [3] | 李洋, 李丽娜. 基于模糊层次分析法的供应商选择[J]. 森林工程, 2008(9): 79–84. |
| [4] | 张英, 冯艳芳. 基于模糊层次分析法的大学生综合素质评价[J]. 武汉理工大学学报: 社会科学版, 2007(10): 707–710. |
| [5] | 杨霞芳, 律星光. 基于FAHP的供应商选择与评价指标体系[J]. 物流科技, 2012(2): 25–30. |
| [6] | 罗非.我国稀土供需预测研究[D].北京: 中国地质大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-11415-1012364938.htm |
| [7] | Keith R Long, Bradley S Van Gosen, Nora K Foley, et al.The principal rare earth elements deposits of the United States-A summary of domestic depositsand a global perspective[R].Washington, D C: U.S.Department of the Interior.U.S.Geological Survey, 2010. |
| [8] | Thomas G Goonan.Rare earth elements-End use and recyclability[R].Washington, D C: U.S.Department of the Interior, U.S.Geological Survey, 2011. |
| [9] | Daniel J Cordier.Rare Earths[R].Washington, D C: U.S.Geological Survey, 2012. |
| [10] | Pui-Kwan Tse.China’s rare-earth industry[R].Washington, D C: U.S.Department of the Interior U.S.Geological Survey, 2011. |
| [11] | Marc Humphries.Rare earth elements: The global supply chain[R].Darby: DIANE Publishing, 2010. |
| [12] | Joseph Gambogi, Daniel J Cordier.Rare Earths[R].Washington, D C: U.S.Department of the Interior, U.S.Geological Survey, 2012. |
| [13] | Greta J Orris1, Richard I Grauch.Rare Earth Element Mines, Deposits and Occurrences[R].Washington, D C: U.S.Department of the Interior U.S.Geological Survey , 2002. |
 2013, Vol. 4
2013, Vol. 4

