| 不同岩石脆性破坏声发射时频特性及信号识别 |
2. 河北联合大学,a.矿业工程学院;b.河北省矿业开发与安全技术重点实验室,河北 唐山 063009
2. a.Faculty of Mining and Engineering;b.Hebei Province Mining Industry Develops with Safe Technology Priority Laboratory,Hebei United University,Tangshan 063009,China
岩石声发射现象可反映出岩石损伤过程中所包含的诸多信息,一般可通过研究岩石受力破裂过程的声发射特性来认识岩石破裂机理,从而为岩石声发射监测技术提供理论依据[1].
目前,许多岩石力学专家学者借助声发射技术研究岩石渐进破裂失稳过程,对受载岩石破裂过程声发射活动规律、能量分布以及频率演化特性等进行了研究,并初步实现岩石破裂声发射源的定位;同时部分学者利用BP 神经网络方法,在传统声发射源定位法的基础上对声发射信号进行模式识别,实现高精度定位;还有在岩石微破裂分形特征的基础上,结合声发射参数和幅度进行了神经网络的识别研究等[2-9].岩石破裂损伤声发射信号模式识别的研究并不多,但在机械故障诊断及其它人工固体材料的无损检测等领域,声发射信号的模式识别已颇为成熟[10-11].在实际工程中,岩体稳定性的监测对象往往岩性各异,其失稳破坏声发射监测预测及信号识别还存在可靠性差等问题.因此,对不同岩石受载破裂过程声发射特性差异进行分析,综合考虑声发射参数、频率特性及能量分布等作为模式识别特征向量,有望增强岩石破裂过程声发射监测能力,提高信号识别精度.
1 不同岩石声发射试验对3 类岩样进行岩石声发射试验,试验系统如图 1 所示.试验装置由RMT-150C 型岩石力学测试系统和SAEU2S 型声发射系统两部分组成.试验过程中,通过对岩样在试验机上进行单轴加载,控制加载速率为0.002 mm/s, 同时采集加载过程中声发射信息.
 |
| 图 1 声发射试验系统 |
岩样包括变粒岩、花岗岩和石灰岩.其中,变粒岩取自金矿围岩,加工成圆柱体(Φ50 mm×100 mm)试样,编号B-N (B 代表变粒岩,N 指第N 个试样,下同),呈青灰色,结构致密,造岩颗粒细致,节理裂隙不发育;花岗岩取自露天矿,加工成立方体(50 mm×50 mm×100 mm)试样,编号H-N,呈银白色并含黑斑,造岩矿物颗粒较粗;石灰岩取自锡矿围岩,加工成立方体(50 mm×50 mm×100 mm)试样,编号S-N,呈灰色,矿物颗粒细致,含少量裂隙.
2 岩石破裂过程声发射特性分析 2.1 声发射特征参数比较分析岩石的单轴抗压强度(简称σc)因其本身物理属性的差异而不尽相同,不同岩样破裂损伤时裂纹产生、扩展及破坏方式等的不同,导致与之相对应的声发射各种特征参数也存在较大区别.从试验过的3 类岩样中各自选取2 个试样的试验数据,进行以下各种分析与探讨.研究表明,如果岩石在破坏前应变的大小低于2 %,可认为此变形过程为脆性破坏[12].如图 2所示,变粒岩试样在加载开始后很快便进入线弹性阶段并持续到破坏失稳阶段,此时声发射振铃累积计数,由较低水平转而急剧上升直至试样基本丧失承载能力,岩样σc 值较高且在整个加载过程中应变很小,属典型的脆性破坏.花岗岩试样在破坏前一直处于线弹性阶段,振铃累积计数较低且缓慢上升,岩石抗压强度很高(试样H-1 达160 MPa),试样出现的多次片帮导致峰值后的曲线出现了波动,声发射活动剧烈,振铃累积计数上升加快,试样承载能力在一段时间后均突降为零,破裂前总应变小于1.5 %,可归类于脆性破坏.石灰岩S-1 试样曲线演化情况类似于变粒岩,属脆性破坏; 由于S-2 试样内部存在少量裂隙,曲线在开始加载不久便出现波动,试样在峰值附近出现较多轴向贯通裂纹,曲线出现多次较大的波动直到岩样破坏;石灰岩试样单轴抗压强度均较低,虽S-2 试样因含裂隙而略显塑性,但在加载最后阶段,其应力值突减至零,总应变约为1 %,归属于脆性破坏的范围.总之,随应力的增加,变粒岩的声发射振铃累积计数变化幅度最大,花岗岩次之,石灰岩居后;在达到峰值前,大部分岩石声发射参数都发生了不同程度的瞬间增加,均具有一定的前兆特征,且在岩样破坏后,其应变也达到最大,但均在1.5 %范围内.
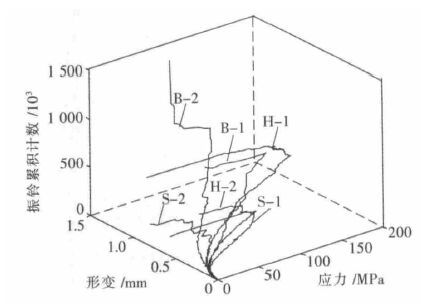 |
| 图 2 应力、形变与声发射振铃累积计数关系 |
根据3 类岩石声发射振铃累积计数-时间关联图(如图 3 所示)得知,加载时间最长为石灰岩S-2试样、花岗岩次之,变粒岩随后,时间最短为石灰岩S-1 试样.以200 s 时间点为界,在此之前,各类岩石声发射振铃累积计数很小且增加缓慢,而变粒岩声发射振铃累积计数的变化要远大于其它3 类岩石;200 s过后,花岗岩H-1 与石灰岩S-1 的声发射振铃累积计数的变化率瞬间增大,紧接着变粒岩声发射振铃累积计数近乎直线上升;在约400 s 和470 s 时,变粒岩S-1 与花岗岩H-1 声发射振铃累积计数变化率,分别出现第二次瞬间提升,此时为岩石破坏失稳阶段; 花岗岩H-2 与石灰岩S-2 整个加载过程中声发射振铃累积计数变化较平缓,只有临近破坏时才出现小幅度的增大.如图 4 所示,在加载的整个过程中,各类岩样声发射能量率,均在岩石破坏临界点附近大量增加,其中花岗岩H-1 试样在加载不久便出现声发射能量率的大幅度提升,主要是试样因端部效应导致多次片帮的产生,进而使得声发射活动剧烈.
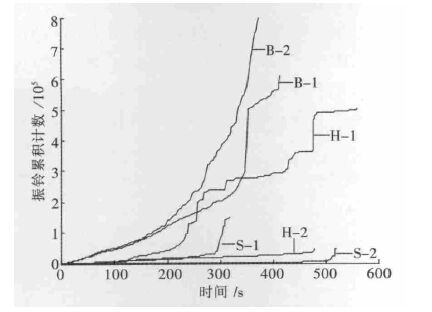 |
| 图 3 声发射振铃累积计数与时间关系 |
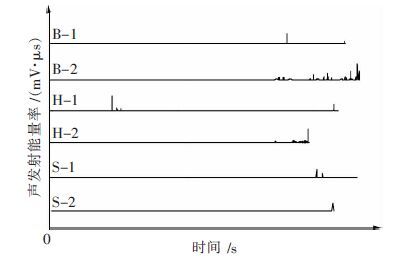 |
| 图 4 不同岩石声发射能量率演化图 |
2.2 声发射信号Welch 谱特征比较分析
信号的功率谱反映了信号携带的诸多重要特征,本文利用Welch 谱估计法对岩石声发射信号进行功率谱特征分析,旨在探讨单轴受压下岩石声发射信号不同频段相对功率谱密度(简称PSD)分布情况.不同岩石的声发射信号功率谱曲线演化情况“大同小异”,即总体上变化情况相似,其PSD 值均是在低频段较大,在高频段较小;不同的是PSD 值较大的频段的范围有所差别.据图 5 可知,变粒岩与石灰岩的PSD 值较大的频段为0 kHz 至(1 000~1 200) kHz, 花岗岩PSD值较大的频段仅为(0~800) kHz; 同类岩石的声发射信号峰值频率大小接近,不同类岩石则有较大差异.
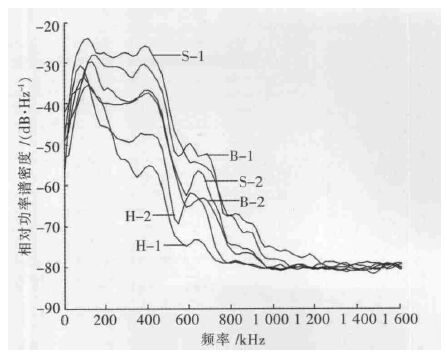 |
| 图 5 不同岩石声发射信号Welch 功率谱图 |
2.3 声发射信号EMD 能量熵比较分析
经验模态分解(EMD) 是一种非常适合于非线性、非平稳信号的分析方法,其本质是对信号进行平稳化和线性化处理,把复杂的信号分解成有限个瞬时频率有意义、幅度或频率受调制的本征模态分量(IMF)[13].EMD 技术已广泛应用于爆破震动及设备诊断等[14-15]诸多领域,并取得良好效果,但在声发射尤其是岩石损伤声发射信号处理方面的研究不多.
岩石声发射信号一般分为连续型、突发型和混合型[16].不同岩石损伤过程中各种类型声发射信号,经EMD 分解后的各IMF 分量,分别代表了一组特征尺度下的平稳信号,各平稳信号能量的变化就表征了岩石声发射信号的特征情况.基于IMF能量的声发射信号特征提取方法[13]:对目标声发射信号进行EMD 分解,选取含主要信息的前n个IMF分量,然后求各IMF的能量,即

|
以能量比为元素构造一个向量T=[E1/E,E2/E,…,En/E],此向量称为EMD 能量熵,即表征了信号的特征,其中
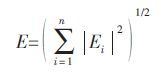
|
单轴压缩下岩样声发射信号经EMD 分解后得到11 个IMF 分量,如图 6 所示,分量c1 是声发射信号中分解出的时间尺度最短、频率最高的分量,一般指声发射信号的白噪音;c2 为信号的高频,振幅较大;c3、c4 均为信号的优势频率子频带,振幅大,所占能量较大;c6~c10 为声发射信号分解出的低频分量,振幅较小;R 代表该信号微弱的趋势.
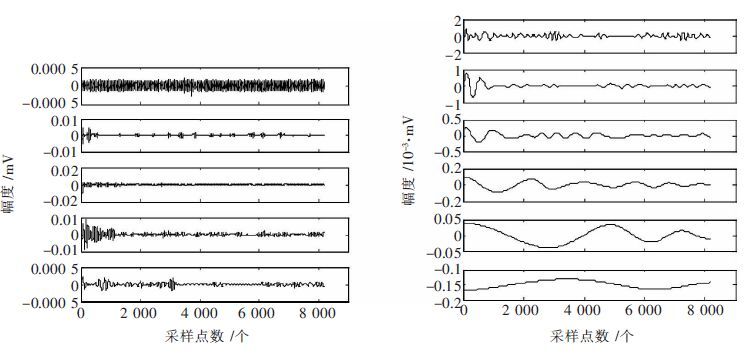 |
| 图 6 岩石损伤声发射信号EMD 分解图 |
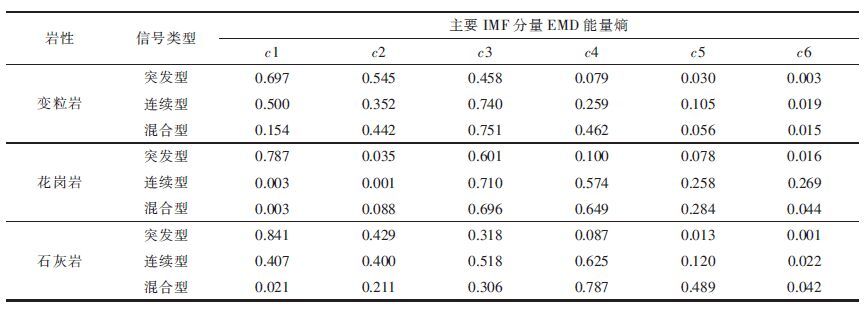
按照声发射信号特征提取方法计算经筛选的IMF 分量的能量熵,以此作为表征岩石损伤各类声发射信号的特征向量,见表 1.对比岩石声发射信号能量熵特征可知,变粒岩声发射信号大部分能量集中在c1~c4 分量内,花岗岩和石灰岩突发型信号能量分布在前3 个分量中,花岗岩连续型与混合型则分布于c3~c5,石灰岩连续型声发射信号分布于c1~c5,混合型信号集中在c2~c5 分量内;各种岩石突发型声发射信号第一个IMF 分量的能量熵均很高,大部分连续型信号主要IMF 分量的能量熵分布较为均匀.
| 表1 不同岩石的声发射信号EMD 能量熵 |
 |
| 点击放大 |
3 基于BP 神经网络的岩石声发射信号识别 3.1 BP 神经网络结构
对岩石声发射信号或机械噪音的声发射参数、峰值频率及能量分布等差异量化后,便可作为识别不同声发射信号的特征量.设计的BP 神经网络结构包括输入层、隐含层和输出层,其中输入层节点数为11,分别为岩石声发射上升时间、振铃计数、能量、持续时间、幅度、峰值频率以及前5 个IMF 分量的能量熵;输出层节点数为3,其中变粒岩用001 表示,花岗岩为010,石灰岩为011,机械噪音为100,人为噪声用101 代替;根据文献[1]可知隐含层节点数的范围为[4, 14],设计选取14.经对比,隐含层的传递函数采用tansig 函数,输出层神经元传递函数选择logsig 函数.
3.2 BP 神经网络的训练与测试训练样本包括岩石声发射信号及干扰信号各30 组,期望输出用二进制代码(001、010、011、100、101)表示,测试样本包括岩石声发射信号及干扰源信号各20 组.训练采用RPROP 算法,目标函数误差为0.001,最大迭代次数为5 万次,训练结果如图 7所示.
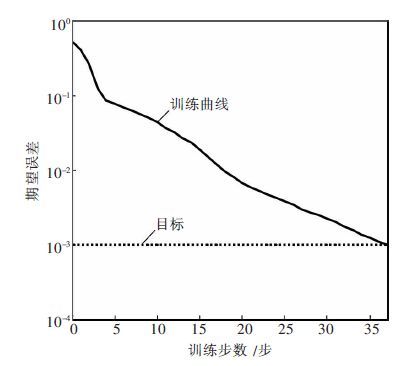 |
| 图 7 网络训练误差变化曲线 |
经过37 次训练,达到指定的最小期望误差0.001.用训练网络对岩石声发射信号及干扰噪声的测试数据进行识别,识别率最低的是花岗岩声发射信号(识别率为80 %),易被误识别为人为噪声,主要原因是由于人为噪声的随机性较大;机械噪音与人为噪声的识别率均达100 %;变粒岩识别精度为95 %,有一组信号被误判为人为噪声; 石灰岩的识别精度为90 %,其中有一组识别为变粒岩声发射信号,一组识别为人为噪声.岩石声发射信号及干扰噪声平均正确识别率达93 %,证明该网络具较强的学习能力,能够达到自动识别声发射信号类别的目的.
4 结论(1)单轴加载下岩石破裂声发射特征参数随应力或时间的演化情况存在异同,不同点是声发射特征参数(振铃累积计数与能量率)在岩石整个加载过程中的变化幅度与速度等的差异,共同点是指其在岩石失稳破坏临界点出现瞬间增加或大幅度提升.
(2)针对3 类岩石破裂过程声发射信号,EMD与Welch 谱估计法能很好地表现出不同信号频谱与能量分布的特征差异,并显示出较强的鉴别能力.
(3)结合声发射参数、峰值频率及EMD 能量熵等多种特征,设计并训练出能对单轴加载过程中不同岩石声发射信号识别效果良好的BP 神经网络,平均识别精度达90 %以上.
5 建议针对单轴加载下岩石破裂损伤声发射信号,在分析不同岩石的声发射参数特性的基础上,提出了基于Welch 谱与EMD 的特征提取方法,结合BP 神经网络对不同岩石的声发射信号进行了识别.岩石受载损伤声发射特征参数方面的研究已较为成熟,对于岩石声发射信号频域特性分析及识别还有待进一步研究,尤其对多种岩石声发射特征的定量研究还有待于大量实验数据的积累和归纳.
| [1] | 刘祥鑫.不同岩石声发射时频特性及其信号识别技术研究[D].赣州: 江西理工大学, 2012. |
| [2] | 康志强, 于洋, 李闻杰. 岩石受压破裂过程应力应变及声发射特性研究[J]. 金属矿山, 2011(2): 22–24. |
| [3] | 赵兴东, 陈长华, 刘建坡, 等. 不同岩石声发射活动特性的实验研究[J]. 东北大学学报: 自然科学版, 2008, 29(11): 1633–1636. |
| [4] | 纪洪广, 王宏伟, 曹善忠, 等. 花岗岩单轴受压条件下声发射信号频率特征试验研究[J]. 岩石力学与工程学报, 2012, 31(s1): 2900–2905. |
| [5] | 凌同华, 张胜, 易志强, 等. 岩石声发射信号能量分布特征的EMD分析[J]. 振动与冲击, 2012, 31(11): 26–31. |
| [6] | 许江, 李树春, 唐晓军, 等. 单轴压缩下岩石声发射定位实验的影响因素分析[J]. 岩石力学与工程学报, 2008, 27(4): 765–772. |
| [7] | 吴永胜, 余贤斌. 单轴压缩条件下岩石声发射特性的实验研究[J]. 金属矿山, 2008(10): 25–28. |
| [8] | 吴贤振, 刘祥鑫, 刘洪兴. 砂岩岩爆声发射特征及b值动态特性试验研究[J]. 金属矿山, 2011(3): 16–18. |
| [9] | 张省军, 刘建坡, 石长岩, 等. 基于声发射实验岩石破坏前兆特征研究[J]. 金属矿山, 2008(8): 65–68. |
| [10] | 王海丽, 马春翔, 邵华, 等. 车削过程中刀具磨损和破损状态的自动识别[J]. 上海交通大学学报, 2006, 40(12): 2057–2062. |
| [11] | 杨璧玲, 张同华, 张慧萍, 等. 基于声发射信号模式识别的UHMWPE/LDPE复合材料损伤机制分析[J]. 复合材料学报, 2008, 25(2): 35–40. |
| [12] |
Griggs D L, Handin J. Rock deformation[J].
Geol.Soc.Am.Mem., 1960, 79: 23–26. |
| [13] | 徐锋, 刘云飞. 基于EMD的胶合板损伤声发射信号特征提取及神经网络模式识别[J]. 振动与冲击, 2012, 31(15): 30–35. |
| [14] | 李夕兵, 张义平, 左宇军, 等. 岩石爆破振动信号的EMD滤波与消噪[J]. 中南大学学报: 自然科学版, 2006, 37(1): 150–154. |
| [15] | 高强, 杜小山, 范虹, 等. 滚动轴承故障的EMD诊断方法研究[J]. 振动工程学报, 2007, 20(1): 15–18. |
| [16] | 耿荣生, 沈功田, 刘时风, 等. 基于波形分析的声发射信号处理技术[J]. 无损检测, 2002(6): 257–261. |
 2013, Vol. 4
2013, Vol. 4


