| 一种考虑表层原子结构的纳米接触近距离分子间作用计算方法 |
微电子机械系统(Micro-Electro-MechanicalSystem: MEMS) 或称微型机械是机械科学技术的前沿领域[1].MEMS 具有体积小、质量小、能耗低、集成度和智能化程度高的特点.由于微加工的尺寸和形状精度还远不能和宏观机械相比,其摩擦磨损更加严重.MEMS 在其制造过程和工作过程中摩擦和粘着等摩擦学问题严重影响了其可靠性[2-7]
当微表面静止接触或两表面间隙处于纳米量级时,由于表面接触力使其两表面接触在一起.Sandi 国家试验室的J.A.Walraven 在2003 年总结MEMS 的4 个主要失效机理时认为,其中3 个失效都与接触有关[7].因此研究纳米接触对MEMS 等微纳米装置的设计具有重要意义.
假设有A、B 两个物体相接触,A、B 均为单质.要对它们进行纳米接触分析,必须引入两个表面之间的粘着.根据Hammaker 三假设[8]可以通过如下步骤计算粘着力.首先,通过考察物体A 整体对B 物体中单个原子的作用势,计算得到物体A 整体对B 单个原子的作用力.然后再对B 中每个原子所受到的来自A物体的作用力累加,以此来研究它们之间的粘着力.可见研究物体A 整体对B 物体单个原子的作用势对粘着的计算有重要影响.这里主要考虑此作用势,并将其标记为E.而将A 物体中单个原子对B 物体中单个原子的作用势表示为e.
有学者应用该方法仿真得到的仿真结果与实验事实定性相符[9-11].
A 物体的表面形貌对E 在不同位置的强度有影响,Roger A.Sauer 认为垂直于A 表面的法线方向上的E 强度可以通过引入平面半无限体假设来进行近似计算,并且证明在A 表面曲率半径大于8 nm 的情形下,这种简化带来的误差不超过5 %[11].
下面将分别采用积分法和数值法,并引入平面半无限体假设,对一个碳单质物体对一个碳原子的作用势函数进行计算.
1 积分法基于Hamaker 三假设用连续方法进行纳米接触仿真是目前工程上广泛采用的方法.Hamaker 三假设:①离散模型可加性假设:任何两个物体之间的作用力由构成该两个物体的原子对之间的作用力累加求和得到;②连续介质假设:任何物体由数值密度为ρ 的dV 连续构成.③均质材料假设:任何物体,数字密度ρ 和引力常数不变.
根据Hamaker 的3 个假设,E 的表达式如下:
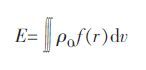
|
(1) |
式(1)中:ρO为原子密度,即单位体积内原子的个数;f(r)为A 中单个原子与B 中单个原子的作用势函数.
ρO可以通过密度、原子量计算得出.f(r)则可以通过实验或者通过第一性原理理论计算双原子系统的结合能,得到一系列的数据点,然后通过对数据点进行拟合来得到.Lennard-Jones 势函数是一种半经验势函数.它具有非常简洁的形式,因此常用于原子间作用势的拟合.Lennard-Jones 势函数的表达式如下:
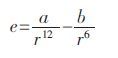
|
(2) |
式(2)中:a、b 为与原子类型有关的常数.
常用的拟合方法有平衡位置求解方程法和最小二乘拟合法[12].
对于平衡位置求解方程法,要求解的方程组形式如下:
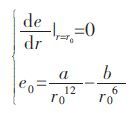
|
(3) |
式(3)中:r0 为两原子达到力平衡时的距离,即势阱位置;e0为势阱深.
该方法在势阱附近具有较好的精度,而在较远处精度很差.
最小二乘法的思想是使得拟合曲线在整个考察范围内的每个数据点处具有最小的误差,而数据点在距离r 上的取值范围可以认为控制在比较有意义的范围之内,因此在此采用最小二乘法拟合.
采用第一原理计算了2 个碳原子在不同距离下的结合能,采用最小二乘法将数据点拟合成Lennard-Jones 势函数,见图 1(a) .
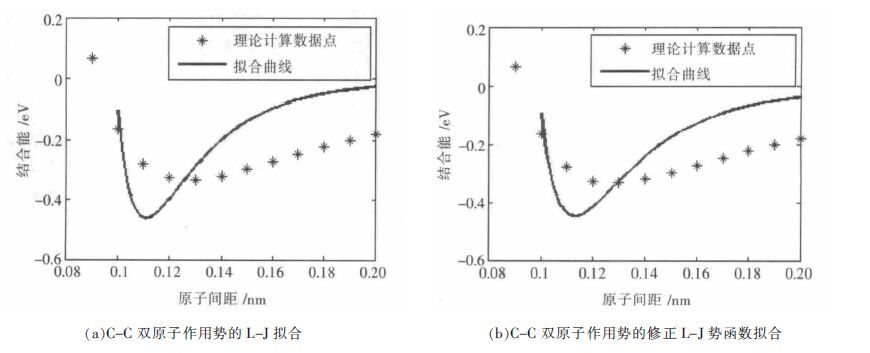 |
| 图 1 Lennard-Jones 势函数拟合与其修正势函数拟合对比 |
由图 1(a)可知拟合的效果并不理想,势阱位置以及曲线的走势和数据点有较大误差.势阱位置明显左移,除少数点外,与第一原理计算得到的数据点相距较远.
有学者指出对Lennard-Jones 势函数进行修正可以更好地与数据点相符[13],其表达式如下:
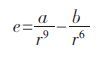
|
(4) |
用修正过的势函数进行拟合,效果见图 1(b) .由图 1(b)可见整体拟合效果较修正前略好,但是仍然不令人满意.
接下来计算平面半无限体A 对单个碳原子在不同距离下的势能E.在极坐标下计算,式(1)可改写为:
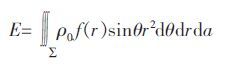
|
(5) |
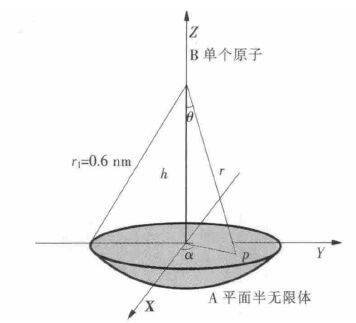
积分区域如图 2 .计算结果为下式:
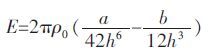
|
(6) |
其中h 是单个碳原子到平面的距离.由积分法得到的计算结果可知,积分法并不具备任何能够体现物质结构的参数.也就是说,它不能区分不同物质结构对粘着力的影响.比如对于石墨和金刚石,其计算结果是相同的.
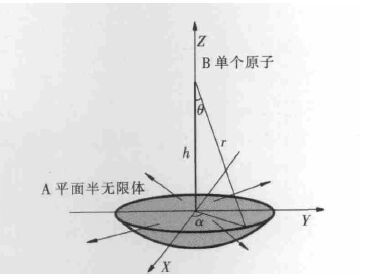 |
| 图 2 积分方法计算平面半无限体对单个原子作用势(E)的积分区域(浅蓝色部分) |
2 数值方法
实际物质是由离散的原子构成的.对于固体,尤其是晶体来说,其微观结构在短程和长程都具有周期性.若忽略晶体中存在的缺陷,那么晶体固体可以视为由相同的、均匀的微观结构(晶胞)堆砌而成的.田文超等[14]考虑了由晶体结构内部存在的原子“空穴”对计算结果进行了修正,取得了一定效果.但此方法有两点缺陷.一是对于晶体近表面的分子间作用势,这种方法依然不精确;二是将原子视为均匀的可产生作用势的球体,这一假设存在理论上的缺陷.
若对于晶体固体把Hamaker 三假设的后两条中关于数字密度e 的假设改为:晶体固体在任何部分具有相同的均匀的微观结构,那么就可以通过对固体中的原子对原子作用势进行求和.这里将此方法称为数值求解方法.数值求解方法中,应将A 物体视为由一个个原子构成,则E 的表达式为:
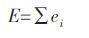
|
(7) |
其中ei为A 物体中序号为i 的单个原子对B 中单个原子的作用势,其大小由原子的种类和距离决定.此距离为原子核距离.
纳米接触分析中,极近距离(明显小于固体中原子间距)下的作用势e 不用考虑,而在考虑范围内曲线的导数变化并不剧烈,因此这里通过对离散数据点线性插值求解ei 就有足够的精度.这就避免了拟合函数带来的问题.而数据点是有限的,较远的原子作用势无法考虑.不过,较远处原子对E 的实际贡献很小,这里暂时选择忽略.将截断后计算的平面半无限体对单个碳原子的作用势记为El.本次计算将原子间的作用势e 在超出0.6 nm 的距离上定义为0.为简化问题,忽略了界面效应.
采用matlab 进行计算.将可能出现在0.6 nm 范围内的原子,及其原子核位置一一列出,然后求取当B 原子在不同高度h 上与它们的距离.根据距离在e离散点上插值求得ei,最后将所有ei 累加求得不同高度h 上的EI.
考虑A 物体中原子的分布状况,首先选取石墨晶体,以其解理面为平面半无限体的表面进行计算.选取了石墨解理面上的两个点,向上沿着其法线方向分别计算E,取点的位置和计算结果见图 3.
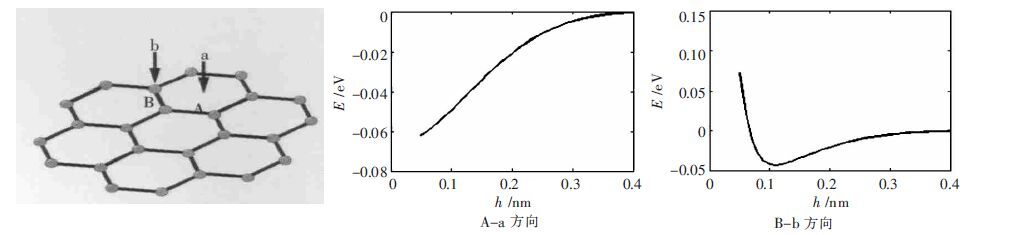 |
| 图 3 石墨表面不同位置上方El 的曲线对比 |
晶体解理面被认为是自然界最平滑的表面,而由图 3 可见,即使是非常平滑的表面上,其势场分布也极不均匀.该结果体现了数值法在计算近距离作用中的优势,可以预计数值方法在计算斥力方面的潜力.同时,这也是AFM 可以达到原子级分辨率的原因.为取得方便实用的结果,可以对石墨表面各个点的作用势取平均,其结果见图 4 中Ela 曲线.然后计算金刚石晶体,同样取其解理面为平面半无限体的表面进行计算,计算结果同样见图 4.
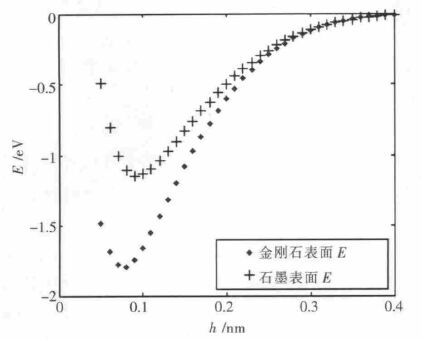 |
| 图 4 金刚石与石墨表面Ela 的曲线对比 |
比较石墨和金刚石两种平面半无限体对单个碳原子作用势的计算结果可以发现,物体表层的原子结构对物体表面的作用势有重要的影响.
3 两种计算方法的比较以及对数值计算方法的误差估计与修正由于数值方法在0.6 nm 上对e 进行了截断.所以为了严格地比较2 种计算方法,将积分方法也进行一个截断,即在图 5 所示的积分区域内积分计算.行比较,可以发现计算结果差距非常明显(见图 6).
 |
| 图 5 区域内比较两种计算方法的差距 |
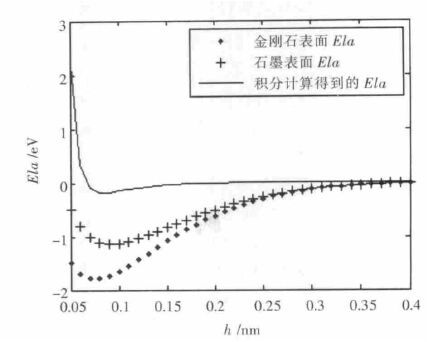 |
| 图 6 两种计算方法得到的Ela 结果 |
分析其原因是因为积分计算未考虑物质的实际结构,而e 的曲线存在一个先下降后上升,先正后负,最后趋近于0 的变化过程.采用积分计算方法会造成正负势能抵消,使得积分的计算结果远小于数值计算的结果.因此积分计算方法仅适用于较远距离的引力计算[15].
由于数值计算方法无论在对e 的处理方面还是物质实际结构的考虑上均优于积分计算,所以在仿真计算中采用数值计算方法可以获得更好的结果.
不过由于数值计算存在截断带来的误差,所以还必须对这个误差加以分析.
参考图 1(b)可以发现在较远处,修正后的Lennard-Jones 势函数和数据点符合较好.在较远处,e 的变化很慢,且均<0,所以对于截断产生的误差可以通过积分求解来进行估计.误差函数Ee 计算表达式同式(6),而积分区域不同.其积分区域见图 7 .求解得到的结果如下:
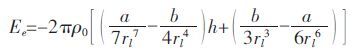
|
(8) |
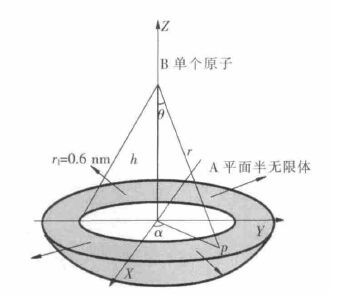 |
| 图 7 区域上积分估算截断误差 |
其中rl 为截断距离.图 8 描述了修正后的石墨表面Ela 的曲线变化情况.将修正后的数值计算结果(Ea)和未修正的计算结果比较发现差别很小,故实际计算中可考虑不进行修正.由此可以推断,在表面几层原子之外的原子对其表面的Ea 影响不大.考虑到物质中原子间距和分子间作用势相关,因此推断Ea 主要受表面1~2 层原子结构的影响.
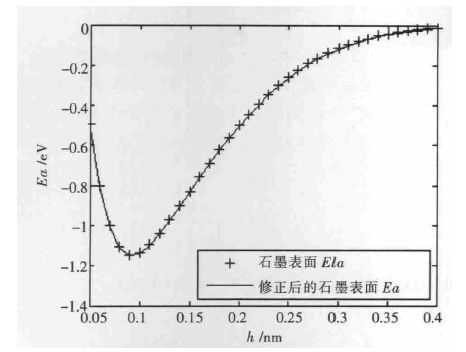 |
| 图 8 对截断误差进行修正后发现结果变化不大 |
4 结论
首先采用积分计算方法计算了碳单质平面半无限体对单个碳原子的作用势.之后采用数值计算方法,分别计算了石墨和金刚石平面半无限体对单个碳原子的作用势E.计算结果表明积分方法与数值计算的结果差距很大.这是由于积分法计算不能体现物质的微观结构,以及在拟合双原子系统势函数时伴随的误差带来的.在数值计算过程中发现物体表面尤其是较短距离内的作用势具有高度的不均匀性,且受到表面1~2 层原子结构很大影响.
由于数值方法较精确地考虑了物质表面的微观结构,并且在得到ei 的过程中具有比积分方法所采用的函数拟合具有高得多的精度,可以认为数值计算方法更加合理.在实际计算中,数值方法更具潜力,但是依然存在不足.例如,数值计算方法需要对表面原子结构的信息有更详细的了解.因此该方法有待进一步研究以便实用化.
致谢: 感谢江西理工大学王观石博士对本文提出的宝贵意见.| [1] | 徐泰然. MEMS和微系统的设计与制造[M]. 北京: 机械工业出版社 , 2004. |
| [2] |
Lorenz C, Chandross D, Gress M, et al. Tribological properties of alkysilane self-assmbled monolayers[J].
Langmuir, 2005, 21: 11744–11748. DOI: 10.1021/la051741m. |
| [3] |
Bushan B. Microelectronies and nanometer structures[J].
J Vae.Sci.Technol.B, 2003, 21: 2262–2296. DOI: 10.1116/1.1627336. |
| [4] | 雒建斌, 何雨, 温诗铸, 等. 微纳米制造技术的摩擦学挑战[J]. 摩擦学学报, 2005, 25(3): 283–288. |
| [5] | A Morrow C.Adhesive rough surface contact[D].Pittsburgh: University of Pittsburgh, 2004. http://cn.bing.com/academic/profile?id=9bad1a915099628ccf9e641f61a40ebd&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] |
Bharat B. Nanotribology and nanomechanics of MEMS/NEMS and BioMEMS/BioNEMS materials and devices[J].
Microelectronic Engineering, 2007, 84(3): 387–412. DOI: 10.1016/j.mee.2006.10.059. |
| [7] | A Walraven J.Failure mechanisms in MEMS[C]//ITC International Test Conference, 2003: 823-834. |
| [8] |
Hamaker H C. The London-vander weals attraction between spherical particles[J].
Physica, 1937, 4(10): 1058–1072. DOI: 10.1016/S0031-8914(37)80203-7. |
| [9] | 田文超, 贾建援. DMD弹性片同基底之间的粘着力计算[J]. 仪器仪表学报, 2003, 24(4): 528–530. |
| [10] | 赵靖松.MEMS粗糙表面接触研究[D].西安: 西安电子科技大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10701-2008056053.htm |
| [11] |
Roger A Sauer, Peter Wriggers. Formulation and analysis of a three-dimensional finite element implementation for adhesive contact at nanoscale[J].
Computer Methods in Applied Mechanics and Engieering, 2009, 198. |
| [12] | 刘艳侠, 孙佳佳, 高岩, 等. 关于Lennard-Jones型势函数参数的几种拟合方法[J]. 辽宁大学学报: 自然科学版, 2008, 35(3): 206–209. |
| [13] | 张福田. 分子界面化学基础[M]. 上海: 上海科学技术文献出版社 , 2006: 207. |
| [14] | 田文超, 贾建援. Hamaker连续介质假设分析[J]. 物理学报, 2008, 57(9): 5378–5382. |
| [15] | 范国滨, 田文超, 贾建援. Hamaker假设工程实际应用的作用域讨论[J]. 机械科学与技术, 2004, 23(5): 532–533. |
 2013, Vol. 4
2013, Vol. 4

