| 基于RBF神经网络的WO3浸出率软测量建模 |
2. 赣州华兴钨制品有限公司,江西 赣州 341000
2. Ganzhou Huaxing Tungsten Products Co.Ltd., Ganzhou 341000, China
钨的湿法冶炼工艺流程[1]主要包含磨矿、碱煮分解、压滤除渣、离子交换、APT 结晶等工序.其中矿物分解作为生产过程中的初始工序,矿物的浸出率和反应速率直接影响整个生产过程的原料回收率和生产效率,因此对钨浸出率的实时检测就显得十分重要.目前我国大部分钨冶炼厂检测钨碱煮浸出率主要是用人工定时取样,化验室试剂滴定分析的方法[2],这种方法不具有实时性.因此开发钨碱煮浸出率的实时检测系统,能为钨冶炼自动化提供基础的检测手段.
1 钨碱煮工艺浸出率传统检测目前国内多数厂家采用碱煮法分解钨矿[3],使用合适浓度的苛性钠溶液与钨矿反应[4],生成钨酸钠和相应金属的氢氧化物.反应式如下:
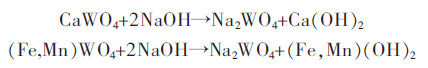
|
钨碱煮分解的浸出率是指钨酸钠溶液中WO3的含量与参与反应原始矿物中氧化钨含量的百分比.钨碱煮分解浸出率的计算公式:

|
(1) |
式(1)中:[WO3]为钨酸钠溶液中三氧化钨浓度.钨酸钠溶液体积和精矿重量较易测量.钨矿中WO3含量是由钨矿的品位决定,数据由供货商提供.所以测定钨矿浸出率的关键问题就是测定钨酸钠中氧化钨的含量.
在实际生产过程中,一个碱煮周期需要约6~7 h不等.碱煮浸出过程,由人工定时取得反应釜中料液,送至化验室滴定检测出浸出液中的WO3含量,从而判断反应程度是否达到预期程度.
但人工检测存在的问题如下:
(1) 人工检测有可能会错过最佳的检测时机,导致检测结果无法显示当前状态.
(2) 化验是一个比较复杂且耗时的过程,因此采用化验方法则无法实现在线实时检测.
因此提出软测量方案.在线实时检测的优势在于:
(1) 能够实时检测浸出率变化,有利于准确调整浸出进程的控制参数到最佳值.
(2) 在刚好达到最佳浸出率的时候,可以及时开始下一道工序,以节省加热加压的能耗.
2 浸出率软测量方法 2.1 碱煮浸出过程模型钨矿的碱煮过程可分为以下几个步骤:
(1) NaOH 溶液通过机械搅拌作用扩散到矿物颗粒团;
(2) NaOH 溶液由浓度差产生的渗透力扩散到矿物颗粒表面液膜;
(3) 溶液中的离子与矿物分子发生复分解反应,在颗粒表面产生反应生成物.
(4) 搅拌作用下,生成物脱离矿粒.李军等[5]的研究表明,反应生成的铁锰氧化物自动脱落,未反应完的残余矿粒表面不会产生氧化物薄膜;
(5) 后续未完成反应的矿粒表面由搅拌和浓度差渗透力再次积聚钠离子和氢氧根离子.此时,微观意义上来说,钠离子和氢氧根离子浓度已经降低.
为便于分析碱煮的动态过程,把连续的碱煮过程在时间上进行离散化,在空间上进行网格化.微元体积内的各个碱煮参数在微时间段内可视作恒定值[6],相邻微时间段参数的变化受到反应条件的影响.假设当前时刻碱煮过程的内参数集可以用A 来表示,上一个微时间段系统内参数集为A’.抽象化的碱煮过程模型可以用公式表示:
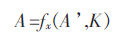
|
(2) |
式(2)中:A 表示一个微元体积内的氢氧化钠,钨矿矿粒、反应生成物的量.K 表示微元内的温度、压力、流体流速、流体黏度等条件参数. fx则表示的是特定条件下钨碱煮输出与输入的函数关系.
2.2 碱煮浸出率软测量模型实现软测量最重要的两个步骤是选取起主导因素的辅助变量与通过辨识的方法建立模型[7].软测量的基本框架如图 1 所示.
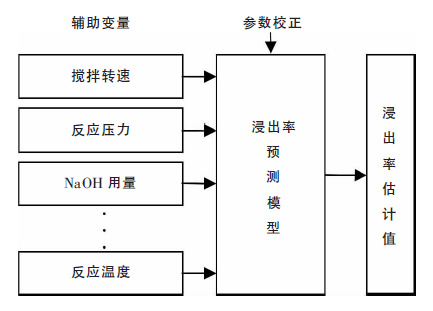 |
| 图 1 浸出率软测量基本框图 |
通过构造所有容易测量的过程变量[θ1,θ2,…,θn]到浸出率估计值$\hat{y}$的映射,可用数学表达式表示为:
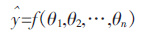
|
(3) |
式(3)中函数f 即为要构造的辅助变量到待测浸出率间的映射关系.$\hat{y}$表示浸出率估计值,[θ1,θ2,…,θn]表示对浸出率有影响的各个参数.
2.3 输入变量选取与样本数据收集选择合适的输入变量是成功实现钨浸出率软测量技术的先决条件.钨碱煮浸出过程是一个复杂的非线性多变量的物理化学过程[8].即使在相同的初始条件下(即相同的原料配比,相同的钨矿品位,符合标准的碱液浓度),但由于受到环境温度、通风条件、大气压强变化和设备老化等外界不确定因素的影响,反应的过程和结果会不相同.依据钨碱煮浸出的反应机理,在此选用最易受外界干扰的反应参数作为软测量的输入,这样才能实时追踪反应参数的变化,进而用软测量模型估计出在此反应条件下的钨浸出率[9].依据文献[10]的研究结果和实验分析,得出影响反应最终浸出率的因素有:苛性钠用量及原料配比、反应温度、反应器内部压力、反应时的搅拌强度等.
因此选用温度、压力以及搅拌转速这3 个过程参数作为神经网络的输入[11].苛性钠用量,原料配比作为初始参数也作为神经网络输入.
选定输入参数(辅助变量)后,收集生产过程历史数据和来自工厂的样品分析数据作为神经网络训练样本.依据文献[12]的研究结果,整理并记录数据样本集合.
3 RBF 神经网络软测量建模建立软测量模型有3 种方式[13]:机理建模、神经网络建模、混合建模.由于神经网络建模具有简便快捷等优势,因此采用神经网络构建模型.
3.1 人工神经网络基本原理人工神经网络是基于生物神经网络活动机理抽象出来的一种简易模型,能够简易的模拟人脑的活动,例如形象记忆、模式识别、非线性映射.神经网络的最基本结构就是神经元,神经元作为神经网络的某个节点,接收上一层输出的加权和作为输入,经过激发函数转换成神经元输出[14].神经网络是一个并行和分布式的信息处理网络结构,它一般由许多个神经元组成,每个神经元只有一个输出,它可以连接到很多其他的神经元,每个神经元输入有多个连接通道,每个连接通道对应于一个连接权系数.神经网络的基本结构如图 2 所示.
 |
| 图 2 人工神经网络结构 |
这表示网络结构具有n 个输入节点,k 个隐层节点和一个输出节点.对应的权重矩阵Wih和Wj分别是输入层到隐层的连接权重和隐层到输出层的连接权重.
3.2 神经网络结构与数据归一化首先确定神经网络的结构,人工神经网络包含输入层、隐藏层和输出层.隐藏层的神经元的个数确定由实际应用情况确定,太少的隐藏层神经元个数将会影响训练精度,太多的神经元数量又将会增加网络训练难度和训练速率.神经网络输入变量总共有5 个,即温度、压力和搅拌转速以及苛性钠用量和原料配比.所以输入层有5 个神经元.网络只有浸出率这个参数输出,所以输出层有一个神经元.
由于采样数据的量纲以及数量级相差比较大,所以在训练之前需要对采样数据进行归一化处理,之后神经网络才能更为准确的处理标准化的样本数据.一般的归一化方法[15]是将所有数据规整到[0,1]区间.归一化公式如下:
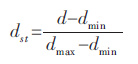
|
(4) |
式(4)中:dmin为采样数据最小值,dmax为采样数据最大值,dst为归一化后的数据,d 为归一化前的数据.
对于神经网络的输出数据,还需要进行反归一化处理,反归一化公式:
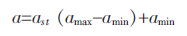
|
(5) |
式(5)中:amax为采样数据最大值,amin采样数据最小值,ast为神经网络输出的标准值,a 为反归一化之后的值.
3.3 神经网络训练方法与结果在实际中,由于RBF 网络具有广泛的非线性适应能力,学习速度快,能避免局部最小值问题,所以 RBF 网络应用较为广泛,因此采用RBF 网络训练软测量模型.RBF 是一种只有单隐层的神经网络,输入层直接传输信号到隐含层,经过隐含层的径向基函数运算,隐层的输出加权后传输到输出层.
RBF 网络使用的基函数采用高斯函数:
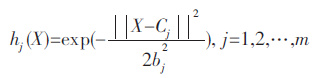
|
(6) |
式(6)中:hj (X)为隐层中第j 个神经单元输出,X 是输入向量,包含温度、压力和时间等各个输入参数.Cj为隐层第j 个径向基函数的中心,bj为对应基函数的宽度.
网络的输出:
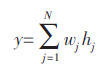
|
(7) |
式(7)中:y 表示的神经网络的预测输出,wj表示的是隐层第j 个神经元到输出层的权重.
信息在神经网络中正向传播得到网络的输出值,输出值与实测值比较得到训练误差,再根据误差值调整隐含层的基函数的中心Cj、宽度bj和输出权值wj.
采用带动量因子的梯度下降法进行网络参数训练,即在计算当前时刻的网络参数时,前一时刻的网络参数变化也参与到运算中去.具体算法[16]流程:
首先定义一个目标函数:
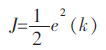
|
(8) |
计算预测误差:
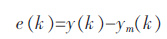
|
(9) |
式(9)中,y(k)为k 时刻的浸出率化验结果,ym(k)为 k 时刻的神经网络计算结果.
隐含层节点到输出节点的连接权计算公式:
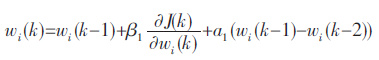
|
(10) |
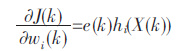
|
(11) |
式(10)、式(11)中,wi(k)为k 时刻隐层第i 个神经元到输出节点的权值,X(k)为k 时刻对应的输入向量的值.
径向基函数中宽度的计算公式:
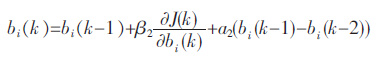
|
(12) |

|
(13) |
径向基函数中心的计算公式:
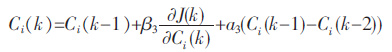
|
(14) |
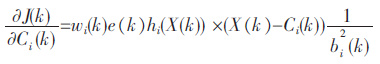
|
(15) |
式(12)~(15)中i=1,2,…,n,n 为隐层神经元个数;β1、β2、β3为学习效率,一般取不同值,α1、α2、α3为遗忘因子,一般也不相同.加入了学习效率和遗忘因子项,有助于增强网络对工况的适应能力.当网络误差变化很大时[17],它能够使网络发散变慢,从而使网络趋于收敛.
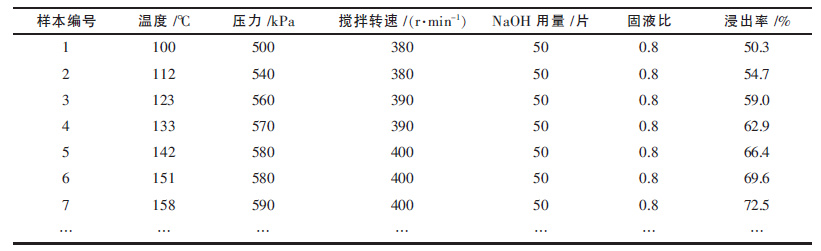
部分样本数据如表 1 所示.RBF 神经网络软测量模型训练完成后,采用其中一次浸出取样的数据进行 WO3浸出率离线预测.网络训练的收敛过程如图 3 所示,软测量预测值和化验值对比如图 4 所示,预测误差如图 5 所示.由图 3 可知,神经网络的收敛速度控制在可接受范围内.从图 5 可知,软测量预测值和实际化验值的误差在-0.5 %至0.5 %之间,预测精度达到检测要求.
| 表1 部分样本数据 |
 |
| 点击放大 |
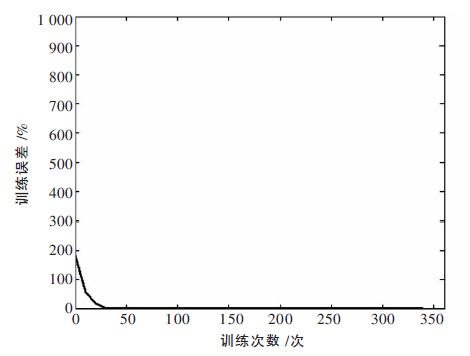 |
| 图 3 RBF 网络训练收敛过程 |
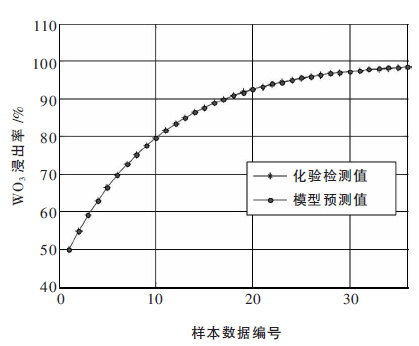 |
| 图 4 WO3浸出率预测值和离线化验结果对比 |
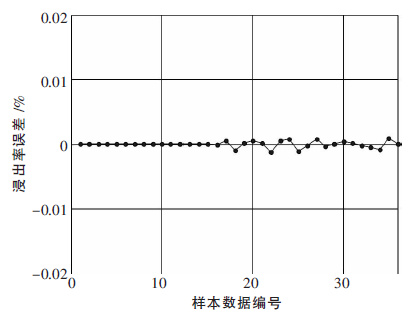 |
| 图 5 WO3浸出率预测值和离线化验结果误差 |
4 结论
提出了软测量方案用于钨矿碱煮浸出率检测,采用RBF 网络构建软测量模型,运用采样数据训练神经网络,并分析网络预测结果.总结如下:
(1)鉴于不便用机理建模方法实现WO3浸出率的在线检测.根据浸出过程机理,选取搅拌转速、压力、温度、苛性钠用量和原料配比作为模型输入参数.
(2)对建立的模型离线训练,神经网络模型的测量结果和化验结果对比,发现软测量模型的测量精度达到预期目标.
| [1] | 李洪桂, 羊建高, 李昆. 钨冶金学[M]. 长沙: 中南大学出版社 , 2010: 49-51. |
| [2] | 陈树茂. 论提高钨冶炼金属回收率的有效途径[J]. 稀有金属与硬质合金, 2004(2): 39–41. |
| [3] | 廖春发, 杨文强, 王旭, 等. 由钨酸盐熔盐电解直接制备钨粉的可行性分析[J]. 有色金属科学与工程, 2011, 2(2): 4–6. |
| [4] | 何利华, 刘旭恒, 赵中伟, 等. 钨矿物原料碱分解的理论与工艺[J]. 中国钨业, 2012(27): 22–27. |
| [5] | 李军, 李洪桂, 刘茂盛, 等. 氢氧化钠与黑钨反应动力学研究[J]. 中南矿冶学院学报, 1985(4): 128–136. |
| [6] | 童长仁, 周小雪. 离子交换过程数学模型及仿真研究[J]. 江西有色金属, 2006(4): 32–34. |
| [7] | 曾青云, 汪金良, 张传福. 基于自适应模糊神经网络的铜闪速熔炼渣含Fe/SiO2模型研究[J]. 有色金属科学与工程, 2011, 2(2): 5–8. |
| [8] | 童长仁, 李明周, 吴金财. 基于BP网络逆映射的铝酸钠溶液软测量模型[J]. 中国有色金属学报, 2008, 18(5): 916–922. |
| [9] | 胡广浩, 毛志忠, 何大阔. 浸出过程浸出率预测与在线优化[J]. 系统工程学报, 2011, 26(4): 524–530. |
| [10] | 史海燕, 赵中伟. 苛性钠分解黑钨矿的热力学分析[J]. 中国钨业, 2006(5): 24–27. |
| [11] | 谢昕, 郭鹏飞, 詹小丽. 基于RBF神经网络的余氯浓度预测模型研究[J]. 传感器与微系统, 2012, 31(8): 64–68. |
| [12] | 赵中伟, 梁勇, 刘旭恒, 等. 反应挤出法碱分解黑钨矿[J]. 中国有色金属学报, 2011(21): 2946–2951. |
| [13] | 王莉, 冯丽辉, 张军, 等. 基于神经网络软测量的虚拟仪器设计及实现[J]. 昆明理工大学学报: 理工版, 2005(1): 33–36. |
| [14] | 张愉. 氧化铝浓度的RBF神经网络软测量模型研究[J]. 计算机测量与控制, 2010, 18(11): 2472–2474. |
| [15] |
Mohammed Awad, Héctor Pomares, Ignacio Rojas. Input variable selection in hierarchical RBF networks[J].
Computational Intelligence and Bioinspired Systems, 2005, 3512: 280–288. DOI: 10.1007/b136983. |
| [16] |
HUANG Kai, WANG Le, MA Jin-wen. Efficient training of RBF networks via the BYY automated model selection learning algorithms[J].
Advances in Neural Network, 2007, 4491: 1183–1192. |
| [17] |
Hyontai Sug. Using quick decision tree algorithm to find better RBF networks[J].
Intelligent Information and Database Systems, 2011, 6591: 207–217. DOI: 10.1007/978-3-642-20039-7. |
 2013, Vol. 4
2013, Vol. 4

