| 静载荷与循环冲击作用下岩石损伤变量定义方法的选择 |
b. 应用科学学院,江西理工大学,江西 赣州 341000
b. b. College of Applied Science, Jiangxi University of Science and Technology, Ganzhou 341000,China
爆破开挖工程岩体过程中,围岩体承受的载荷不仅有多次爆破动载荷还有地应力等静载荷,简称静载荷与循环冲击组合[1-3].多次爆破循环冲击应力波不可避免对围岩体造成累积损伤作用[4-6],导致岩石(体)发生动态强度劣化和疲劳变形等现象,造成有别于单次冲击时岩石能量耗散、破坏模式和机理的特性[1-3,7-10].在研究岩石动态疲劳力学特性时,其损伤累积演化规律及疲劳损伤机理是不可回避的问题,这些问题的解决不仅有助于系统掌握岩石在循环冲击载荷作用下强度劣化和疲劳变形规律,对岩石疲劳力学性能的影响因素分析以及了解岩石在随机循环冲击载荷作用下的力学性能也大有益处.
利用损伤力学研究岩石等固体材料在(循环)载荷作用下的力学特性时,必须选择一个合适的损伤变量.作为损伤变量的参数应具备明确的物理意义、便于测量(定)以及变化规律与材料疲劳力学性能演化过程一致等特点.伴随岩石等材料损伤累积过程中,材料的物理力学特性必然发生改变.基于此,目前用于定义脆性材料损伤变量的参数主要有弹性(变形)模量、纵波波速[6,8,9,11]、能量耗散[12]、最大应变[13-14]、残余应变[15]、声发射[16]和密度等.其中,以纵波波速定义岩石(体)损伤变量的方法,在室内试验和现场监测研究中应用较为广泛,取得了较好的效果.
进行循环冲击试验时,由于轴向加载装置的限制,无法放置声波测试仪的探头,不能得到每冲击一次后岩石的纵波波速值,导致不能用纵波波速计算其损伤变量.金解放等[1]的研究结果表明,可以应用岩石波阻抗定义其损伤变量,该方法的优点是波阻抗的物理意义明确,波阻抗值的大小测定相对较方便.
除了可利用波阻抗定义循环冲击过程中岩石的损伤变量,弹性模量、能量耗散、最大应变、残余应变以及声发射能否用来表征其损伤变量,目前没有进行系统研究.本文根据上述物理力学参数定义静态载荷作用下岩石或混凝土损伤变量的方法,基于岩石在静载荷与循环冲击组合作用下的试验数据,研究这些参数定义其损伤变量的可行性.研究结果可为进一步研究岩石在等幅循环冲击或分级循环冲击下的损伤累积演化特性提供理论基础.
1 岩石循环冲击试验及结果 1.1 试验设备和原理设备采用动静组合加载试验系统,如图 1 所示.为了实现冲击过程中应力波为弹性波,入射杆、透射杆和冲头等材质为高强度合金钢,其弹性极限约为725 MPa,波阻抗约为421 MPa/s.
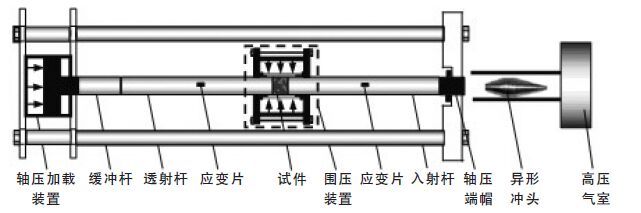 |
| 图 1 动静组合加载试验系统示意图 |
轴压和围压加载装置分别连接手动油压泵,轴压加载装置需要两个油泵,围压只需一个油泵.发射腔内采用异型冲头以消除PC 振荡,实现半正弦波加载.数据采集分别通过入射杆和透射杆上的应变片,借助于超动态应变仪和示波器,分别得到单次冲击的入射、反射和透射应变波.
由试验得到的入射波εI(t)、反射波εR(t)和透射波εT(t),根据一维应力波理论,岩石试件的应力σ(t)、应变ε (t)、应变率$\dot{\varepsilon }$(t)、入射能EI、反射能ER和透射能ET的计算式如下.
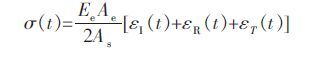
|
(1) |
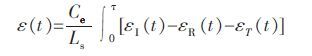
|
(2) |

|
(3) |
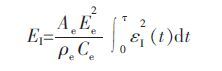
|
(4) |
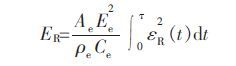
|
(5) |
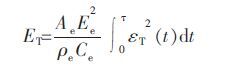
|
(6) |
试件的吸收能EA为:
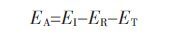
|
(7) |
单位体积吸收能Ev为:
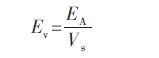
|
(8) |
其中,Ae、Ce和Ee分别是弹性杆横截面面积、声波波速和弹性模量,As和Ls分别是试件横截面积和长度.
1.2 试件制备与轴压和围压的设置岩石试件采用完整性和均质性较好的砂岩制备.试件为圆柱体,直径和长度都为50 mm,两个横截面平行度与平面度严格满足岩石力学试验标准.围压分别设置为4 MPa、8 MPa、10 MPa 和12 MPa等4 个系列.轴向静载荷分别设置为49 MPa、84 MPa、105 MPa 和125 MPa 等4 个系列.
1.3 试验方法试验时,试样两端面均匀涂抹一层黄油,确保试样两端面与入射杆和透射杆间接触良好,并能很好地减小岩石与弹性杆界面摩擦力.循环冲击前,轴压和围压等静载荷同时缓慢施加,施加到设定轴压和围压值时,关闭轴压和围压加载油泵阀门.对同一岩石试件,确保每次冲击时冲击载荷的大小相等.
1.4 试验结果根据轴压和围压的分类,共进行了16 组岩石循环冲击试验.图 2 和表 1 仅表示出围压为8 MPa、轴压为49 MPa 时试验所得的动态应力-应变曲线和相关物理力学参数的试验结果.图 2 中的T3-2-1 为试件编号,1、3、…、15 为循环冲击次数.表 1 中峰值应变、残余应变、加载段变形模量、第一卸载段变形模量等参数的定义或计算方法与文献[2]一致;波阻抗的计算方法请参见文献[1].
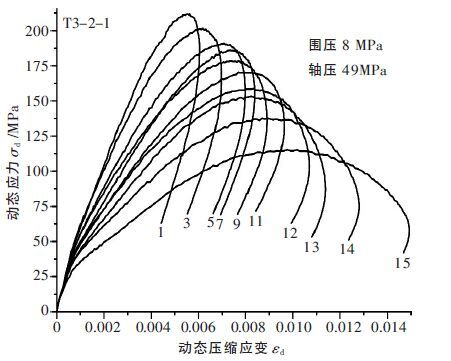 |
| 图 2 动态应力-应变曲线 |
| 表1 参数试验结果 |
 |
| 点击放大 |
2 损伤变量的选择
根据已有连续损伤力学定义岩石损伤变量的方法,结合循环冲击试验结果,对静载荷与循环冲击作用下岩石损伤变量进行选择研究.
2.1 弹性(变形)模量应用弹性(变形)模量定义材料损伤变量是连续损伤力学较早的方法之一.在Kachanov 定义的连续性因子的基础上,根据有效应力和名义应力间的关系,结合线弹性本构关系,材料的损伤变量D 可表示为:
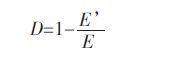
|
(9) |
式(9)中,E’表示材料损伤时的弹性模量,E 表示无损伤时材料的弹性模量.
用弹性或变形模量方法定义岩石损伤变形时,首先应统一确定测定模量的方法.循环冲击作用下岩石动态应力-应变曲线弹性阶段较短[2],其弹性模量不足以体现岩石动态力学特性.加载段变形模量和第一卸载段变形模量能较好地反映岩石动态疲劳力学性能[2].因此,以下主要讨论这两种变形模量定义其损伤变量的可行性.
依据式(9)的定义,E’分别用每次冲击得到的加载段变形模量和第一卸载段变形模量,E 分别用各自第一次冲击的模量值,根据表 1 中的试验结果,计算出的损伤变量D 如图 3 所示.
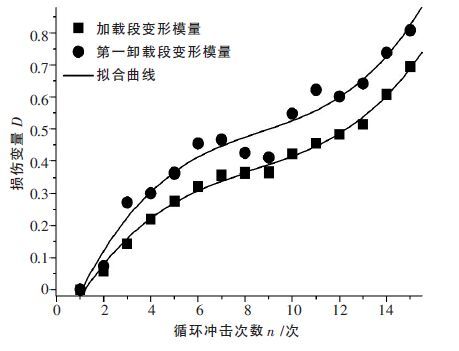 |
| 图 3 基于变形模量计算损伤变量的演化趋势 |
由图 3 可以看出,用两种模量方法计算的损伤变量中,第1 次冲击得到的损伤变量值都为零,这意味着第1 次冲击不能使岩石发生损伤,这明显与实际不吻合.因此,基于变形模量计算静载荷与循环冲击组合作用下岩石的损伤变量不可行.
2.2 声波波速法由弹性波动理论可知,介质纵波波速与其弹性模量和密度有关.根据弹性模量定义损伤变量的方法,可以利用介质纵波波速定义其损伤变量:

|
(10) |
式(10)中,vp为各向同性损伤岩石的纵波波速,vpf为无损伤岩石的纵波波速.利用图 1 所示的装置进行循环冲击试验时,由于轴向加载装置的限制,不能得到冲击损伤时岩石的纵波波速值,因此该方法也不适合.
2.3 能量耗散法岩石等材料在外载荷作用下发生损伤需要消耗能量,即认为材料发生损伤与能量耗散是同步的,并且二者都不可逆.在此基础上,金丰年等[12]的研究表明,可以利用能量耗散定义岩石的损伤变量.
根据式(4)~(8)可知,进行循环冲击试验时,较容易计算得出单次冲击时试件的单位体积吸收能.因此若用能量法定义其损伤变量,可以选择单位体吸收能进行计算,依据能量耗散与损伤间的关系,其计算表达式为:

|
(11) |
式(11)中,Evn有两种表示方法,一是第n 次冲击时的单位体积吸收能;二是第n 次冲击时试件的累积单位体积吸收能.Esum为整个循环作用过程中材料的耗散能量之和.
根据表 1 的试验结果并结合式(11)的定义,利用单位体积吸收能计算的损伤变量如图 4 所示.
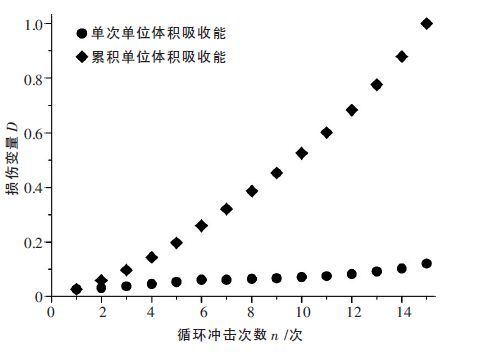 |
| 图 4 基于单位体积吸收能计算损伤变量的演化趋势 |
从图 4 可以看出,用单次单位体积吸收能计算的最终损伤度仅为0.121 4,与岩石发生宏观失效不一致,不能反映岩石最终损伤失效状态,因此该定义方法不适合.用累积单位体积吸收能计算时,最终损伤度为1,能反映出试件的最终破坏失效,但其变化呈光滑匀速上升趋势,不能反映循环冲击过程中岩石疲劳力学性能的初始阶段-低速阶段-加速阶段等过程.因此,式(11)的定义方法不适用于表征循环冲击过程中岩石的损伤变量,需要进一步研究探索利用能量耗散定义其损伤变量的表达式.
2.4 最大应变法在等幅静态或准静态循环载荷作用下,混凝土等材料的损伤变量可以用最大应变进行定义[14].若应用该定义方法计算循环冲击作用下岩石的损伤变量,其计算表达式可写为:
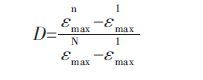
|
(12) |
式(12)中,εmax1 、εmax n 和εmax N 分别表示第1 次冲击、第n次冲击和最后一次冲击得到的最大应变值,即表 1 中的峰值应变.
根据表 1 中的峰值应变值并结合式(12),计算得出的损伤变量随循环冲击次数的变化关系如图 5所示.由图 5 可得,此时的损伤变量的演化趋势明显地包含3 个阶段:初始阶段、低速阶段和加速阶段,能较好地表征岩石在循环冲击作用下的疲劳力学性能.但图 5 中显示第1 次冲击的损伤值为零,不能真实反映实际第1 次的冲击损伤,也不能选用此参数定义岩石的损伤变量.
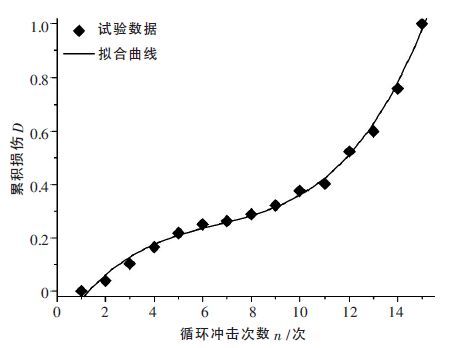 |
| 图 5 基于最大应变计算损伤变量的演化趋势 |
2.5 残余应变法
根据岩石等材料在静态循环载荷作用时利用残余应变定义损伤变量的方法,若利用残余应变计算循环载荷作用下岩石的损伤变量时,其计算表达式可表示为:

|
(13) |
式(13)中,εr n 和εr N 分别为第n 次和最后一次冲击时的残余应变.
由表 1 中残余应变的实验数据,根据式(13)计算的损伤变量随循环冲击次数的变化关系如图 6 所示.由图 6 可知,该方法计算的损伤变量有明显的初始阶段、低速阶段和加速阶段,能反映第1 次冲击引起的损伤,最后一次的损伤值为1,这些都能较好地反映岩石的动态疲劳力学特性.从能否反映岩石动态疲劳力学性能的演化规律、第1 次冲击造成的损伤以及最终的合理损伤等考量,该方法可以定义循环冲击作用下岩石的损伤变量.
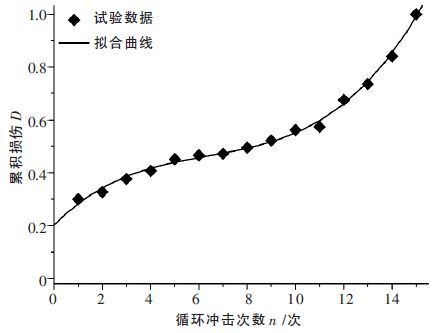 |
| 图 6 基于残余应变计算损伤变量的演化趋势 |
2.6 波阻抗法
波阻抗是岩石等材料动态力学特性重要的物理量,其大小为介质密度和纵波波速的乘积.文献[1]的研究表明,可以用波阻抗定义循环冲击过程中岩石的损伤变量.根据该方法,由表 1 中波阻抗的试验数据,计算得到的损伤变量与循环冲击次数的关系如图 7 所示.
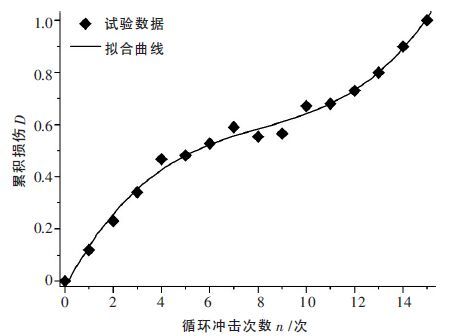 |
| 图 7 基于波阻抗计算损伤变量的演化趋势 |
2.7 声发射法
材料在外因改变时,内部局域源快速释放能量产生瞬态弹性波的现象称为声发射,声发射的产生意味着材料内部出现损伤.因此,声发射可以用来反映岩石的损伤过程[17-18].
在岩石冲击动力学研究中,鲜有应用声发射技术研究岩石的损伤过程.作者认为,其主要瓶颈在于没有有效的方法从大量的应力波信号中区别和提取真正的岩石声发射信号.因为若用声发射信号定义岩石的损伤变量,只有提取出岩石发生损伤而释放的应力波信号才属于声发射信号.在岩石冲击过程中,声发射传感器接受到的信号除了岩石声发射信号之外,还有大量复杂的冲击应力波信号,相比冲击应力波的能量级别,岩石因损伤释放出的弹性应变能微乎其微.因此,若不能从复杂应力波信号中提取真实有效的损伤声发射信号,用声发射定义岩石在循环冲击过程中的损伤变量也不可行.
3 讨论对比图 6 和图 7 可以发现,对同一岩石试件的试验数据,分别用残余应变和波阻抗两种方法计算的损伤变量演化路径不吻合,这主要是由于参数选择以及参数的计算不同引起的.静态载荷作用下选择不同参数定义损伤变量时也会发生这样的现象,例文献[19]中利用疲劳模量和残余应变计算的损伤变量相差也较明显.由于单次冲击过程时间非常短,如图 8 所示,利用式(1)和式(2)计算岩石的动态应力和应变时,受入射波、反射波和透射波的起止点影响较大.当有轴向静载荷时,由于应力波在试件内多次透反射的传播以及轴向静载荷的释放等影响,反射波和透射波终止点的判断受主观因素影响较大,从而影响图 2 所示应力-应变中残余应变的大小,进而影响其计算得到的损伤变量的精确度.
 |
| 图 8 实测单次冲击的应力波 |
另外,由文献[1]可知,波阻抗是岩石动力学最基本、最直观的物理参数.而残余应变是根据动态应力-应变曲线计算得到的衍生参数,且其大小受主观因素影响较大.因此,与波阻抗定义损伤变量相比,用残余应变定义损伤变量精确度较低.
4 结论(1) 从能否反映岩石疲劳力学性能的演化过程、第1 次冲击引起的损伤以及最终损伤度为1 等角度衡量,残余应变和波阻抗都可以定义静载荷与循环冲击组合作用下岩石的损伤变量;变形模量、能量耗散和最大应变等参数则不适合定义其损伤变量.由于没有办法测量其纵波波速和声发射值,这两个参数也不能选用定义静载荷与循环冲击组合作用下岩石的损伤变量.
(2) 利用残余应变和波阻抗计算的损伤变量值有差别,这主要是因为两个参数的计算方法不同导致的.波阻抗定义损伤变量物理意义明确,计算精度较高;残余应变计算得到的损伤变量受主观因素影响较大.
| [1] | 金解放, 李夕兵, 殷志强, 等. 循环冲击作用下波阻抗定义岩石损伤变量的研究[J]. 岩土力学, 2011, 32(5): 1385–1393. |
| [2] | 金解放, 李夕兵, 殷志强, 等. 轴压和循环冲击次数对砂岩动态力学特性的影响[J]. 煤炭学报, 2012, 37(6): 923–930. |
| [3] | 金解放, 李夕兵, 王观石, 等. 循环冲击载荷作用下砂岩破坏模式及其机理[J]. 中南大学学报:自然科学版, 2012, 43(4): 1453–1461. |
| [4] |
Ramulu M, Chakraborty A K, Sitharam T G. Damage assessment of basaltic rock mass due to repeated blasting in a railway tunnelling project - A case study[J].
Tunnelling and Underground Space Technology, 2009, 24(2): 208–221. DOI: 10.1016/j.tust.2008.08.002. |
| [5] |
LI Hai-bo, XIA Xiang, LI Jian-chun, et al. Rock damage control in bedrock blasting excavation for a nuclear power plant[J].
International Journal of Rock Mechanics and Mining Sciences, 2011, 48(2): 210–218. DOI: 10.1016/j.ijrmms.2010.11.016. |
| [6] | 刘明贵, 张国华, 刘绍波, 等. 大帽山小净距隧道群中夹岩累计损伤效应研究[J]. 岩石力学与工程学报, 2009, 28(7): 1363–1369. |
| [7] |
Li X B, Lok T S, Zhao J. Dynamic characteristics of granite subjected to intermediate loading rate[J].
Rock Mech. Rock Eng, 2005, 38(1): 21–39. DOI: 10.1007/s00603-004-0030-7. |
| [8] | 闫长斌, 徐国元, 杨飞. 爆破动荷载作用下围岩累积损伤效应声波测试研究[J]. 岩土工程学报, 2007, 29(1): 88–93. |
| [9] | 林大能, 陈寿如. 循环冲击荷载作用下岩石损伤规律的试验研究[J]. 岩石力学与工程学报, 2005, 22(24): 4094–4098. |
| [10] | 吕晓聪, 许金余, 葛洪海, 等. 围压对砂岩动态冲击力学性能的影响[J]. 岩石力学与工程学报, 2010, 29(1): 193–201. |
| [11] | 赵明阶, 徐蓉. 岩石损伤特性与强度的超声波速研究[J]. 岩土工程学报, 2000, 22(6): 720–722. |
| [12] | 金丰年, 蒋美蓉, 高小玲. 基于能量耗散定义损伤变量的方法[J]. 岩石力学与工程学报, 2004, 23(12): 1976–1980. |
| [13] | 周家文, 杨兴国, 符文熹, 等. 脆性岩石单轴循环加卸载试验及断裂损伤力学特性研究[J]. 岩石力学与工程学报, 2010, 29(6): 1172–1183. |
| [14] | 朱劲松, 肖汝诚, 宋玉普. 混凝土双轴抗压疲劳累积损伤规律试验研究[J]. 土木工程学报, 2005, 38(6): 104–109. |
| [15] | 杨健辉, 方坤河, 赵东拂, 等. 基于残余应变的多侧压下混凝土受拉疲劳损伤研究[J]. 工程力学, 2006, 23(s1): 169–176. |
| [16] | 许江, 李树春, 唐晓军, 等. 基于声发射的岩石疲劳损伤演化[J]. 北京科技大学学报, 2009, 31(1): 19–24. |
| [17] |
Tang C A, Xu X H. Evolution and propagation of material defects and Kaiser effect function[J].
Journal of Seismological Research, 1990, 13(2): 203–213. |
| [18] | 张明, 李仲奎, 杨强, 等. 准脆性材料声发射的损伤模型及统计分析[J]. 岩石力学与工程学报, 2006, 25(12): 2493–2501. |
| [19] | 杨润年, 魏德敏. 钢纤维混凝土等幅弯曲疲劳加载下的疲劳应变和疲劳模量以及损伤研究[J]. 工程力学, 2012, 29(11): 99–102. |
 2013, Vol. 4
2013, Vol. 4

