| 剧烈塑性变形对块状镁合金微观组织和力学性能的影响 |
2. 华中科技大学材料成形与模具技术国家重点实验室,武汉430074
2. State Key Laboratory of Materials Processing and Die & Mould Technology, Huazhong University of Science and Technology, Wuhan 430074,China
镁合金是一种新型的金属材料,它具备高强度、高刚度、强电磁屏蔽能力和耐辐射能力.具有等轴晶的超细晶镁合金广泛应用于汽车、电子、航空航天和国防等领域.许多国家将其视为21 世纪重要的战略资源,并提出了许多研究和发展计划.在这种背景下,研究超细晶镁合金的细化机制和生产过程是十分重要的.为了使镁合金在工业领域有良好的应用,提出了许多提高镁合金力学性能的方法.细化晶粒和控制结构是一种有效地提高金属材料性能的方法.细化晶粒可以提高镁合金在室温下的强度、延展性和超塑性成形能力.
晶粒细化的方法有很多,如挤压、锻造、轧制及其之后的再结晶退火过程.等通道转角挤压(ECAP)作为一种成形技术,能够细化材料组织、改善性能,现已在塑性成形领域得到广泛应用.等通道转角挤压原理如图 1 所示.等通道转角挤压是将工件压入模具以实现大剪切变形量的工艺.在变形过程中,工件从模具通道强行挤出,材料发生剪切变形,获得大的剪切应变,从而细化晶粒.等通道弯角挤压模具是由具有相同横截面积的竖直通道和水平通道相交接而成,并形成两个交接角,即模具拐角Φ 和模具圆心角Ψ [1-2].利用该方法可制备出亚微米级超细晶显微结构的铝[3-6],铜[7-8],镁[9-11],钛[13,14]等金属或合金.不同的工艺参数对经ECAP 变形后的镁合金的组织和性能有不同的影响[15].本文选取了模具拐角、模具圆心角、摩擦力和挤压道次4 个工艺参数进行模拟,并对模拟结果进行了分析.
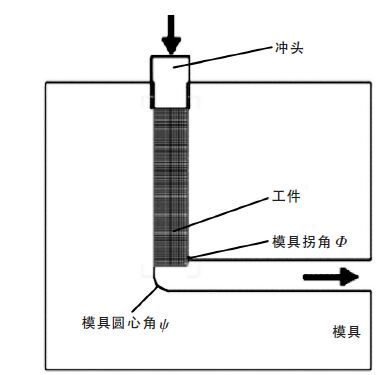 |
| 图 1 等通道转角挤压示意图 |
1 模拟分析
在模拟过程中,挤压件材料为镁合金AZ31,尺寸为12 mm×12 mm×60 mm,网格划分数为10 000,假设挤压件为刚塑性,其应力应变关系为σ =C$\varepsilon \overset{m-n}{\mathop{\varepsilon }}\,$ ,其中C=205 MPa,应变硬化参数m=0.114,n=0.044,挤压速度是10 mm/s.由于镁合金在室温下塑性很差,模拟时设模拟温度为250 ℃.
1.1 模具拐角的影响对于模具拐角,主要研究90°、100°、110°和120°4 种情况,利用DEFORM 软件对上述不同模具拐角挤压过程进行分析,获得挤压件的等效应力分布、等效应变分布和加载载荷曲线,通过对等效应力和等效应变以及加载载荷的分析,确定合理的模具参数.
从图 2 分析不同模具拐角下挤压件的等效应变的分布可以发现,90°拐角时挤压件的最大等效应变较大且挤压件上的等效应变分布与等效应力的分布情况基本相同.由此可见模具拐角为90°比其他3 种模具拐角的变形范围更广,变形量更大,挤压件在流经模具拐角处应变最大,且靠近内拐角处获得的等效应变最高,而内拐角处获得的最高等效应变正是挤压件所需要获得的主要变形,是挤压件通过ECAP 工艺达到细化晶粒目的的主要方式.从图 3 看出挤压载荷随着模具拐角的增大,挤压载荷逐渐减小.在实验设备均能满足上述要求的情况下,在模具工艺设计过程中应结合能源消耗综合考虑.
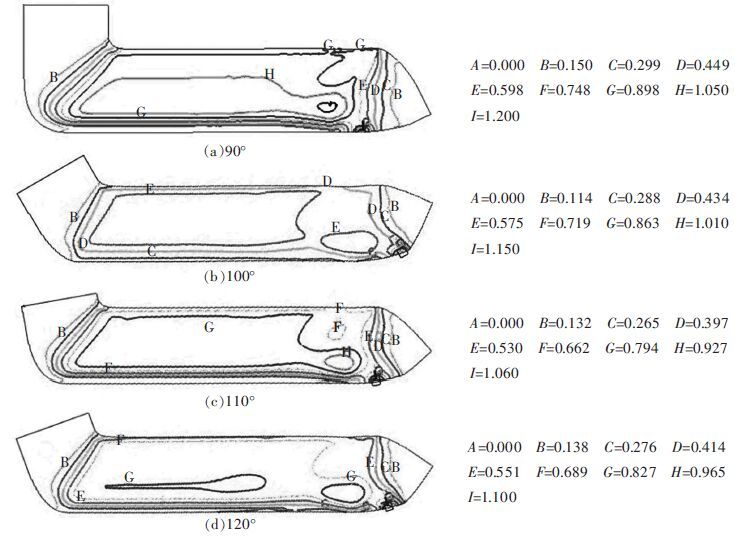 |
| 图 2 不同模具拐角时,挤压件的等效应变分布情况 |
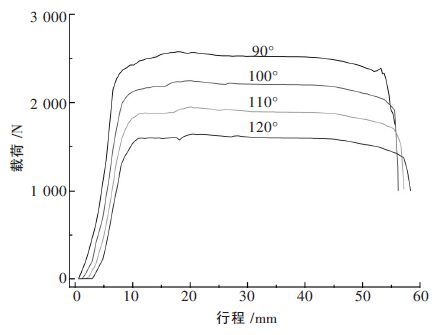 |
| 图 3 不同模具拐角的挤压载荷-行程曲线 |
1.2 模具圆心角的影响
图 4给出了模具拐角为90°时,不同模具圆心角所对应的工件截面上等效应变分布和有限元模拟等通道转角变形过程中试样形状的变化.从模拟结果可以看出,试样每个部分的变形并不均匀.试样的头部和尾部的变形很小.试样中部的变形相对均匀.试样横截面中间区域的变形要比截面上下部位剧烈,这将对变形的均匀性产生不利的影响.
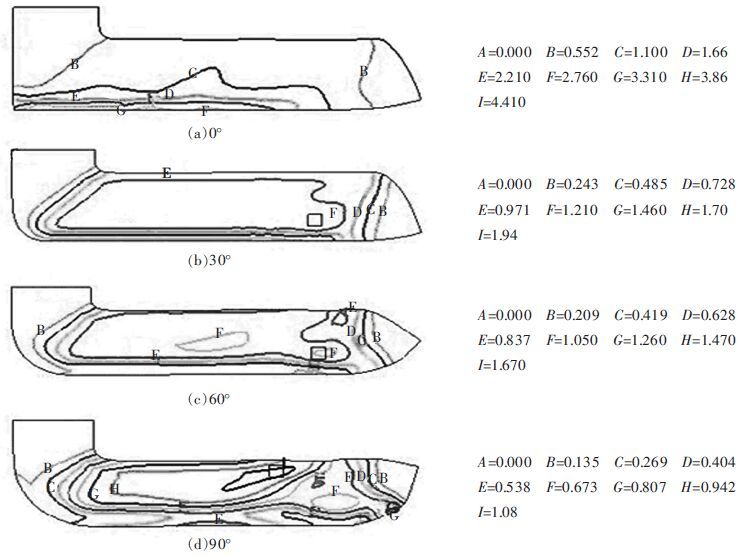 |
| 图 4 不同模具圆心角时,挤压件的等效应变分布情况 |
表 1给出了最大挤压载荷、最大等效应力和最大等效应变之间的关系.随模具圆心角的增大,等效应力有所下降.调整模具圆心角的大小对模具拐角处等效应变的分布有重要影响.但对内拐角处的影响较小.因此当模具拐角处应力较为集中,在模具设计过程中应设计一定倒角,从而避免模具拐角处应力过于集中.挤压件在等效应变的分布大致情况与等效应力相似.模具圆心角越小,等效应变就越大.等效应变从外拐角向到内拐角逐渐增大.模具圆心角Ψ 越大,累积总应变越小.在模具设计中不仅要考虑挤压件变形量的累积,还要考虑到挤压件变形的均匀性和模具圆心角的合理选择,随着圆心角的增大,最大挤压载荷逐渐减小.所以挤压时模具圆心角不宜过小.
| 表1 模具圆心角不同时,最大挤压载荷、最大等效应力和最大等效应变的关系 |
 |
| 点击放大 |
因此,综合考虑挤压过程的等效应力演化规律,挤压后工件的应变累积规律以及载荷变化规律,必须慎重选择模具圆心角.为了获得变形分布更好、应变更高的试样,模具圆心角取值范围一般应等于或略大于30°.
1.3 摩擦的影响摩擦对等通道转角挤压变形具有重要影响.分析不同摩擦条件对挤压过程变形机理的影响,获得挤压件变形分布规律,了解和掌握变形载荷,进而为提高模具寿命提供理论指导.图 5 是不同摩擦因子时,工件的网格变化情况.从模拟结果可以看出,不同摩擦因子时,挤压件的变形情况相似,但变形大小各不相同,且挤压件整体的变形的均匀性也不相同.通过模拟分析,从表 2 可以看出,随着摩擦因子的增大,等效应力增大,但增大趋势不甚明显.因此,摩擦对于改善挤压件的受力大小不明显.从图 5 看出,摩擦因子对等效应变的影响也不是很大.但摩擦因子的大小对挤压载荷的影响十分明显,随着摩擦因子的增加,挤压载荷显著增加,反之亦然.因此,从降低挤压载荷和提高模具寿命角度而言,应尽可能地减小摩擦,即挤压过程中应采取较好的润滑措施,可有效降低挤压载荷,提高模具使用寿命.
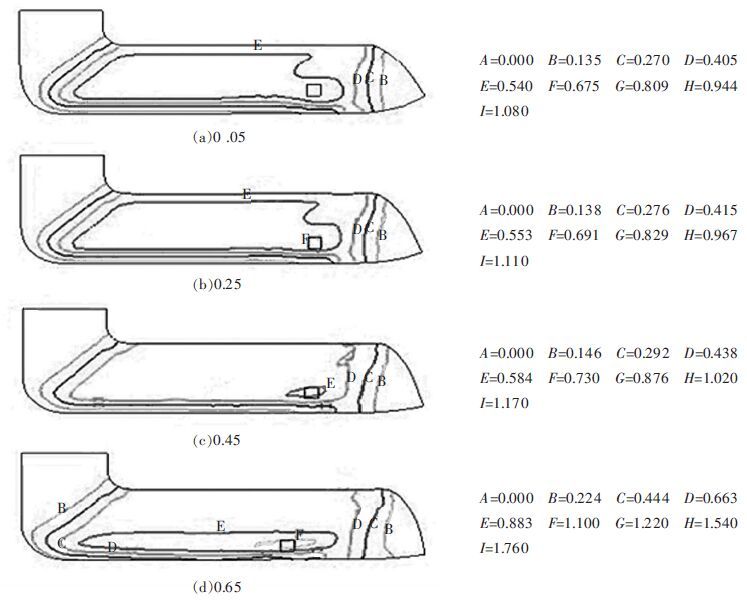 |
| 图 5 不同摩擦因子时,挤压件的等效应变分布情况 |
| 表2 不同摩擦因子时,最大等效应变、最大等效应力与最大载荷的关系 |
 |
| 点击放大 |
1.4 挤压道次的影响
通过对上述模拟结果分析得出,选择合理的模具几何形状以及工艺参数可提高挤压件的变形分布均匀程度与应变累积量,但是单道次ECAP 所获得的挤压件累积变形量较小且变形分布很不均匀.为了获得变形比较均匀的挤压件,挤压件需要累积较大的应变量.因此,多道次挤压有利于累积工件的应变量.本文分别对挤压件进行了4 个道次的模拟,并分析了等效应力和等效应变以及载荷曲线,有利于挤压道次的合理选择.
表 3给出了当模具拐角为90°,挤压道次不同时,最大挤压载荷、最大等效应力和最大等效应变的关系.从表 3 中可以看出挤压4 道次后,通过变形的累积,等效应变随挤压道次的增加而增加.挤压载荷也随着挤压道次的增加而增加,但是增加的幅度并不明显.
| 表3 不同挤压道次时,最大挤压载荷、最大等效应力和最大等效应变的关系 |
 |
| 点击放大 |
图 6给出了挤压道次分别为1、2、3 和4 道次时,等效应变沿横截面高度的分布曲线.挤压件经过四道次后的应变分布并不均匀.从上表面到下表面,等效应变呈现先增加后降低的趋势.变形主要集中在挤压件的中部,上下表面的变形较小.从图 7 还可以看出从第1 道次到第4 道次挤压件的应变逐渐累积,应变逐渐增大.重复挤压以后,挤压件的晶粒受到了不同水平的细化,挤压载荷也相应提高.综上所述,挤压件具有最佳性能,即指获得一定的应变的同时应力不会太高.
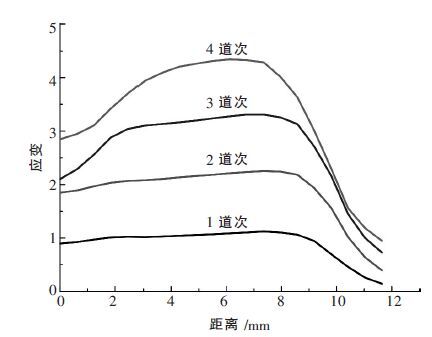 |
| 图 6 X=35 截面挤压件4 个道次的等效应变的分布 |
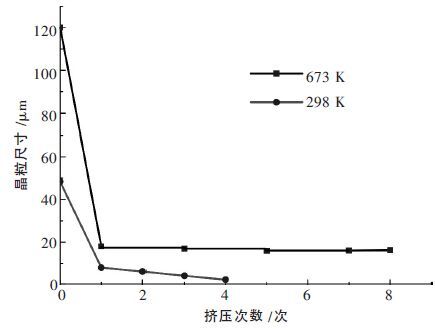 |
| 图 7 不同温度下挤压道次与晶粒尺寸之间的关系 |
2 ECAP 对镁合金力学性能的影响 2.1 AZ31 镁合金经ECAP 变形微观组织的演变
通过DEFORM 模拟了AZ31 镁合金ECAP 变形晶粒网格的变化,通过分析可以看出,ECAP 可以使 AZ31 镁合金晶粒得到细化.而许多科研人员也通过实验证实了这一观点.冯晓明和艾桃桃[16]在673 K 下,对镁合金进行ECAP 变形,并观察了不同道次挤压下材料内部显微组织的变化.未经ECAP 变形的原始晶粒尺寸约为120 μm,经过一道次挤压后,晶粒尺寸降低到18 μm 左右,晶粒明显得到细化.随着挤压次数的增加,晶粒进一步得到细化.通过图 7 可以看出温度对晶粒尺寸的影响是十分显著的.随着温度的增加,晶粒粗化,晶粒尺寸增加.因此,在满足工艺要求的情况下,应尽量选择较低的温度.
2.2 AZ31 镁合金经ECAP 变形力学性能的变化 2.2.1 屈服强度和抗拉强度AZ31 镁合金经ECAP 后随着挤压道次的变化,力学性能也发生相应的变化.未挤压时材料的屈服强度为182.5 MPa,经过1、2 道次挤压后合金的屈服强度略有降低,分别降低了5.47 %和8.22 %.出现与 Hall-Petch 公式不符合的现象,这是因为屈服强度受到晶粒尺寸和织构的影响.ECAP 过程中,4 道次挤压前织构的最大极密度不是很大,织构变化并不明显且形成的都是软取向织构,因此屈服强度的提高主要是晶粒细化的结果;而传统挤压不同,经过温热挤压后,晶粒极大细化且形成方向平行于挤压方向的{0001}基面纤维织构,由于{0001}基面纤维织构是硬取向织构,室温拉伸时基面很难发生滑移,因此在一定程度上提高了合金的屈服强度,晶粒的细化作用加上织构的强化作用是传统挤压材料的屈服强度高于ECAP态材料的原因.经ECAP 4 道次变形以后,晶粒更加细小,织构也得到加强,屈服强度和抗拉强度得到了很大提高.因而随着道次的增加,合金的微观组织的均匀性增加,织构也逐渐得到加强,屈服强度开始随着晶粒的减小而增加,2、3、4 道次屈服强度也逐渐提高,四道次后屈服强度能达到215.3 MPa,由此可以看出AZ31 镁合金经4 道次ECAP 变形后,屈服强度得到明显提高.四道次后抗拉强度达到311.2 MPa,也得到相应提高.因此,四道次后可以明显改善AZ31镁合金的强度.
2.2.2 宏观硬度AZ31 镁合金经ECAP 变形后,宏观硬度有显著提高.试样随挤压道次增加,宏观硬度值有显著增加.刘自乾等[17]通过实验分析了不同道次对材料力学性能的影响.如图 8 所示.未经过ECAP 变形工件的原始硬度为43.69 MPa,一道次挤压后材料的硬度63.57 MPa,随道次的增加,硬度也持续增长,3 道次达到饱和,硬度值达到90.81 MPa.4 道次后材料的硬度略有降低并在随后的道次中材料的硬度基本保持一致,没有发生显著的变化.这是由于随着晶粒细化,晶界处位错塞积减少,位错储能降低,同时,晶粒细化,动态回复能力提高.动态回复软化与加工硬化趋于平衡.硬度上升缓慢:4 道次后组织中晶粒基本是细小的等轴晶,晶粒间变形协调更好,整体位错减少,动态回复带来软化效应基本与加工硬化基本趋于平衡.在随后道次,组织微观形貌基本不变.虽然晶粒尺寸随变形的继续有所减低,但是宏观硬度值基本不变.
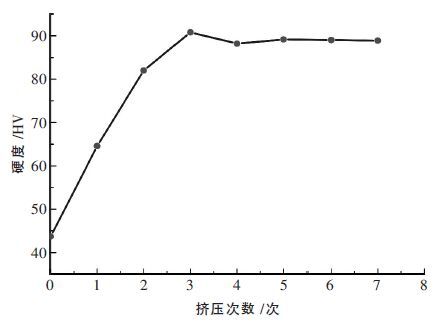 |
| 图 8 挤压道次与宏观硬度的关系 |
2.3 ECAP 变形AZ31 镁合金晶粒尺寸与等效应变的关系
晶粒细化对材料的性能有显著地影响,根据 Hall-Petch 公式可知,随着晶粒尺寸d 减小,材料硬度和强度都有所上升.因此如何简单有效地分析晶粒细化程度便显得至关重要.通过多道次ECAP 工艺,可以使材料内部累积均匀的应变,使晶粒得到细化.然而,至今为止对晶粒细化与累积等效应变分布及均匀程度之间的关系的研究并不多,因此,研究晶粒细化与累积等效应变分布及其均匀程度之间的关系十分必要.
在前期工作的大量实验与理论推导结果的基础上,通过高斯公式建立和推导ECAP 累积等效应变、挤压件组织结构细化后主要变形区平均晶粒度与对应挤压道次下变形材料的力学性能指标之间的定量关系,通过应变的累积,预测超细晶镁合金ECAP 变形后可能达到的平均晶粒度和力学性能.
针对材料晶粒平均几何尺寸大于100 nm 的超细晶材料,其晶粒度对强度的影响可用Hall-Petch(霍尔-佩奇)公式描述为:
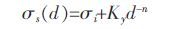
|
(1) |
式(1)中,d 为晶粒平均尺寸,n 随d 有一定变化,典型值一般为0.5,σs为材料屈服强度,通常可用显微硬度Hv来代替,σi为晶粒中位错运动所需的应力,Ky为材料常数.上述公式只是晶粒度与力学性能之间的关系,而采用高斯公式推导可得出主要变形区平均等效应变对应的变形材料的力学性能的新方法:
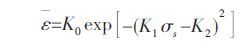
|
(2) |
式(2)中,ε軈是挤压件等效应变,K0是当变形材料达到一定情况的强度和强韧性对应的关键应变,K1是修正的因子,K1∈(0,1),K0和K2是当材料达到一定状态时独立于关键应变和力学性能2 个参数,K2 /K1是一定状态时材料的力学性能值.因此,将式(1)代入式(2),可以建立表征ECAP 累积等效应变和细化晶粒度的新方法:
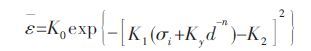
|
(3) |
AZ31 镁合金在2、3、4 道次变形后材料的晶粒尺寸与屈服强度的关系如图 9.经计算得符合Hall- Petch 公式,屈服强度与晶粒尺寸d 成线性关系:σs=σi + Ky*d0.5(σi=85.2,Ky=6.49)[18].前文通过A、C 两种路径模拟了AZ31 镁合金经ECAP 变形后的材料内部的应变关系.经查阅数据4 道次时相关参数K0=4.6,K1=0.049,K2=10,σi=85.2,Ky=6.49 带入式(3)得:
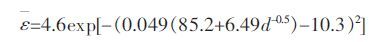
|
(4) |
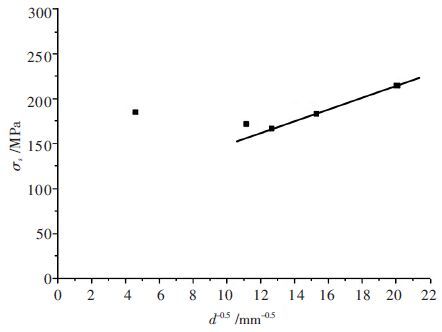 |
| 图 9 AZ31 镁合金屈服强度和晶粒尺寸之间的关系 |
因此可以得到四道次后晶粒尺寸与材料内部应变的关系.A 路径4 道次后累积的应变为4.66;C 路径4道次后累积的应变为4.29.而实验中4 道次后得到的晶粒尺寸是2.5 μm,将其带入式(4),得出ε=4.59,与模拟分析的基本一致.因此可以认为此公式对AZ31镁合金适用.
3 结论(1) 不同的模具拐角、模具圆心角和摩擦因子等对挤压件的应力应变分布、载荷分布及其大小有不同的影响,研究不同工艺参数对挤压件的影响规律,对于获得性能优良、组织均匀的工件具有重要意义.
(2) 通过分析金属变形行为、应变场和挤压件不同挤压路径时应变均匀性分布,发现经过4 道次的挤压后,AZ31 镁合金不仅晶粒得到细化,材料硬度,强度和延伸率也得到了提高.对于多道次挤压来说,发现一条较好的、能够得到均匀的等效应变分布的路径是十分必要的.
(3) 镁合金AZ31 的晶粒细化后的尺寸和力学性能可以通过宏观变形的累积表征来预测.结合改进的模型和微观模拟部分后,可以得到材料外部微观变形、内部微观机制和力学性能的关系.
(4) 通过应变累积可以预测超细晶镁合金的平均晶粒大小和力学性能.如果上述方法能够被大量的实验证明,则可广泛地应用于预测经ECAP 组织结构细化后各种材料的平均晶粒尺寸和力学性能.
| [1] | 张忠明, 王锦程, 唐文婷, 等. 等通道转角挤压(ECAP)工艺的研究现状[J]. 铸造术, 2004, 25(1): 10–12. |
| [2] | 丁茹, 王伯健, 王成. AZ31镁合金晶粒细化方法及机制研究现状[J]. 轻合金加工技术, 2010, 3(1): 99–103. |
| [3] |
Wang J T, Iwahashi Y, Horita Z, et al. An investigation of microstructural stability in an Al-Mg alloy with submicrometer grain size[J].
Acta Mater, 1996, 44: 2973–2982. DOI: 10.1016/1359-6454(95)00395-9. |
| [4] |
Furukawa M, Horita Z, Nemoto M, et al. Microhardness measurements and the Hall-Petch relationship in an Al Mg alloy with submicrometer grain size[J].
Acta Mater, 1996, 44: 4619–4629. DOI: 10.1016/1359-6454(96)00105-X. |
| [5] |
Wang J T, Furukawa M, Horit Z, et al. Enhanced grain growth in an Al Mg alloy with ultrafine grain size[J].
Mater Sci Eng A, 1996, 216: 41–46. DOI: 10.1016/0921-5093(96)10390-7. |
| [6] |
Kawazoe M, Shibata T, Mukai T, et al. Elevated temperature mechanical properties of A 5056Al-Mg alloy processed by equal-channel-angular-extrusion[J].
Scripta Mater, 1997, 36: 699–705. DOI: 10.1016/S1359-6462(96)00446-0. |
| [7] |
Lugo N, Lorca N, Cabrera J M, et al. Microstructures and mechanical properties of pure copper deformed severely by equal-channel angular pressing and high pressure torsion[J].
Mater Sci Eng A, 2008, 477: 366–371. DOI: 10.1016/j.msea.2007.05.083. |
| [8] |
Xu C Z, Wang Q J, Zheng M S, et al. Microstructure and properties of ultra-fine grain Cu Cr alloy prepared by equal-channel angular pressing[J].
Mater Sci Eng A, 2007, 459: 303–308. DOI: 10.1016/j.msea.2007.01.105. |
| [9] |
Loken S, Solberg J K, Maehlen J P, et al. Nanostructured Mg Mm Ni hydrogen storage alloy: Structure-properties relationship[J].
Journal of Alloys and Compounds, 2007, 446: 114–120. |
| [10] |
Zheng M Y, Xu S W, Wu K, et al. Superplasticity of Mg Zn Y alloy containing quasicrystal phase processed by equal channel angular pressing[J].
Mater Letters, 2007, 61(22): 4406–4408. DOI: 10.1016/j.matlet.2007.02.013. |
| [11] |
Matsubara K, Miyahara Y, Horita Z, et al. Developing superplasticity in a magnesium alloy through a combination of extrusion and ECAP[J].
Acta Mater, 2003, 51: 3073–3084. DOI: 10.1016/S1359-6454(03)00118-6. |
| [12] |
Khmelevskaya I Y, Prokoshkin S D, Trubitsyna I B, et al. Structure and properties of Ti Ni-based alloys after equal-channel angular pressing and high-pressure torsion[J].
Mater Sci Eng A, 2008(481/482): 119–122. |
| [13] |
Stolyarov V V, Zhu Y T, Alexandrov I V, et al. Influence of ECAP routes on the microstructure and properties of pure Ti[J].
Mater Sci Eng A, 2001, 299: 59–67. DOI: 10.1016/S0921-5093(00)01411-8. |
| [14] |
Kim J, Kim I, Shin D H. Development of deformation structures in low carbon steel by equal channel angular pressing[J].
Scripta Mater, 2001, 45: 421–426. DOI: 10.1016/S1359-6462(01)01029-6. |
| [15] | 徐淑波.等通道弯角挤压(ECAP)变形机理数值模拟与实验研究[D].济南:山东大学,2006. |
| [16] |
Feng X M, Ai T T. Microstructure evolution and mechanical behavior of AZ31 Mg alloy processed by equal-channel angular pressing[J].
Trans Nonferrous Met Soc China, 2009, 19: 293–298. DOI: 10.1016/S1003-6326(08)60267-8. |
| [17] | 刘自乾, 冯小明, 张会. 等通道转角挤压镁合金的微观组织和力学性能[J]. 金属铸锻焊技术, 2011, 11: 28–33. |
| [18] |
Kim H K. The grain size dependence of flow stress in an ECAPed AZ31 Mg alloy with a constant texture[J].
Mater Sci Eng A, 2008, 515: 66–70. |
 2013, Vol. 4
2013, Vol. 4


