| 基于准时制的铝企业生产作业计划研究 |
工业物流强调对原材料物流的有效管理,包括从原材料的获取到最终产品配送至客户的所有过程.企业主生产计划是在基于对未来销售状况预测或已承诺订单状况的前提下,充分考虑企业现有生产能力(包括资金、设备、人员等),形成合理的产品生产方案(如产品组合、设备生产量等)以保证顾客满意度和实现生产成本最小化或利润最大化.由于生产工艺、市场需求和产品属性的不同,生产计划的制定方式和模型构建也不同.铝企业属于半连续的流程型工业,既有别于离散的机械制造企业,又不同于连续的化工企业,其生产计划问题涉及的内容多、规模大、制造网络结构复杂,建模有一定难度.
从现有研究成果看,钢铁、化工等流程工业生产计划问题研究成果较多.A.C.Hax等[1]针对铝生产企业战略和战术两个层次的决策,基于层次方法建立了两个独立的线性规划模型,一个是与资源计划有关的长期战略计划,另一个是与短期资源利用有关的运作模型,在此基础上,研究了两个模型之间的内在联系,并集成为一个复杂的生产计划系统.M.A.Hariga等[2]研究了一个多产品、多阶段、多周期的铝生产计划编制问题,以铝产品生产成本最小化为目标,建立了包括采购、电解和浇铸在内的线性规划模型.Anantaram等[3]在分析了铝管加工流程的柔性、工序衔接和规模经济的基础上,建立了铝管生产的中期计划模型研究流程生产能力,并采用自适应的流程改进策略处理关键约束.已有的计划模型过于简单或是基于小规模问题,无法描述铝企业实际生产的要求.
本文在综合考虑铝企业工艺流程、生产能力和库存限制等约束条件下,基于生产物流成本及采购成本最小建立铝企业中期生产计划的线性规划模型[4],满足企业生产物流平衡和客户需求的快速响应,实现企业效益的最大化.
1 问题描述和模型建立 1.1 问题描述铝企业生产过程,其主要加工原料有5种,分别为石油焦炭(C)、铝矿石(A)、氟化物(F)、冰晶石(Y)、沥青(P).采购后原料进入企业原料库存,原料通过电解生产线得到铝液,电解之后的铝液被运输到熔铸生产线[5].在熔铸生产线根据不同的产品属性添加不同的合金成分或晶粒细化剂,主要有硅(S)、镁(M)、铜(R)、铁(I)、钛(T)、硼(B)等,得到不同成分的金属液,之后金属液送到浇铸机中进行浇铸,生成多种成分、规格等属性不同的产品,包括标准铝锭(SI)、钛锭(TI)、挤压坯料(EX)、轧制锭(RI)、铝线(BS)等.具体流程见图 1所示.
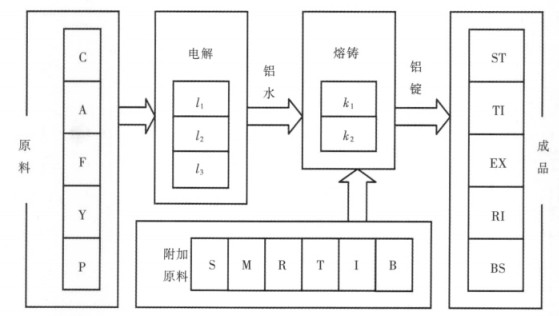 |
| 图 1 铝生产流程 |
铝加工涉及的生产设备、生产资源、最终产品等的属性有很大不同(加工成本、运输成本),原料如何采购、设备和资源如何安排、产品生产多少等都影响着企业的运营效益[6].故企业中期生产计划要解决的问题主要是确定计划期内各种原料和附加原料采购量多少及各条生产线(如电解生产线和熔铸生产线)在各个计划期内产量多少,实现最小生产成本目标的同时保证顾客满意度、优化设备资源利用和生产均衡[7].铝企业生产计划问题涉及的约束条件也较多,主要有不同工序不同设备产能约束,原料、在制品、最终产品库存平衡和企业库存能力约束等.此外为保证各工序之间的衔接匹配,还应满足工序之间物流的协调和一致[8].
在基于订单的生产模式下,保证顾客满意度是铝生产企业应考虑的重要问题,故本文在处理模型的目标函数时基于准时交货期前提下追求生产成本的最小化[9].
1.2 模型建立 1.2.1 基本假设研究模型作如下基本假设[10]:
(1)同一工序不同生产线生产能力和生产成本可以不同,单个生产线不同时间段生产能力保持相同;
(2)不同生产线之间在制品运输成本不同;
(3)原料、附加原料及最终产品库存能力和现有库存为已知;
(4)产品需求预测和已签订单为已知;
(5)电解铝液必须得到完全熔铸;
(6)生产要素市场可提供企业所需原料及原料附加,且不考虑采购的运输成本及购买地价格差异[9];
(7)5种最终产品分别对应5种不同的附加原料比例;
(8)基于铝液单位重量的电解成本和熔铸成本已知,不考虑添加的附加原料.
1.2.2 符号定义模型各符号定义如下:
i:表示原料,i=1,2,3,4,5,分别表示C,A,F,Y,P;
j:表示附加原料,j=1,2,3,4,5,6,分别表示S,M,R,I,T,B;
l:表示电解生产线,l=1,2,3;
k:表示熔铸生产线,k=1,2;
m:表示最终产品,m=1,2,3,4,5,分别表示SI,TI,EX,RI,BS;
t:表示时间段,t=1,2,…,T, T为时间计划期间的段数;
pi:原料i的采购成本;
p’j:附加原料j的采购成本;
cl:电解生产线l的加工成本;
c’k:熔铸生产线k的加工成本;
clk:铝液从电解生产线l到熔铸生产线k的运输成本;
hi:原料i的库存成本;
h’j:附加原料j的库存成本;
h”m:最终产品m的库存成本;
Iit:时间段t末原料i的库存量;
I’jt:时间段t末附加原料j的库存量;
I”mt:时间段t末最终产品m的库存量;
Qilt:时间段t原料i投入到电解生产线l的数量;
Iimax:原料i的最大库存能力;
ri:生产每吨铝液所需原料i的百分比;
CAPlt:时间段t电解生产线l的最大生产能力;
rjm:生产每吨最终产品m所需附加原料j的百分比;
Ijmax:附加原料j的最大库存能力;
CAPkt:时间段t熔铸生产线k的最大生产能力;
Dmt:时间段t最终产品m的需求量;
Immax:最终产品m的最大库存能力;
T:计划期内分为T个时间段;
L:企业有L条电解线;
K:企业有K条浇铸线;
xit:时间段t初原料i的采购量;
x’lt:时间段t电解生产线l生产的铝液重量;
x’lkt:时间段t铝液从电解生产线l到熔铸生产线k的运输量;
x’jt:时间段t初附加原料j的采购量;
x’mkt:熔铸生产线k时间段t最终产品m的产量.
1.2.3 数学模型建立的数学模型如下:
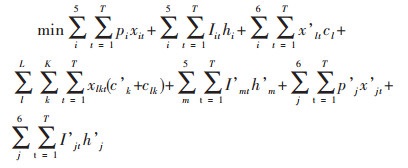
|
(1) |
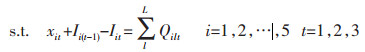
|
(2) |
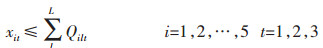
|
(3) |
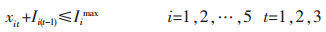
|
(4) |
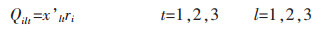
|
(5) |
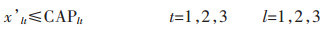
|
(6) |
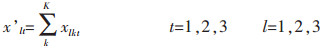
|
(7) |
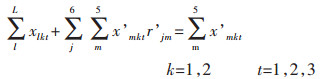
|
(8) |
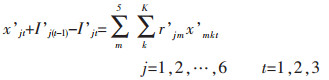
|
(9) |
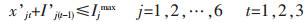
|
(10) |
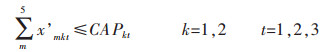
|
(11) |
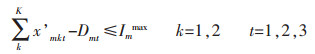
|
(12) |
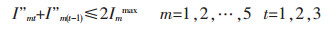
|
(13) |
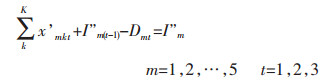
|
(14) |
目标函数(1)表示追求最小的生产成本,包括原料采购成本、原料库存成本、电解成本、熔铸成本、最终产品库存成本、附加原料采购成本、附加原料库存成本[11];约束条件(2)表示原料库存平衡;约束条件(3)确保原料库存随着时间递减[12];约束条件(4)表示原料库存不超过企业最大的原料库存能力;约束条件(5)表示生产流程平衡,即原料必须满足生产需要[13];约束条件(6)表示电解生产线生产能力限制;约束条件(7)表示电解工序运送的铝液必须全部得到浇铸;约束条件(8)表示熔铸生产线物流平衡,即投入等于产出;约束条件(9)表示附加原料的物流平衡,附加原料满足熔铸生产需要;约束条件(10)表示附加原料库存不超过企业最大的附加原料库存能力[14];约束条件(11)表示熔铸生产线生产能力限制;约束条件(12)表示最终产成品库存能力约束;约束条件(13)表示成品库存能力限制[15];约束条件(14)表示成品库存平衡.
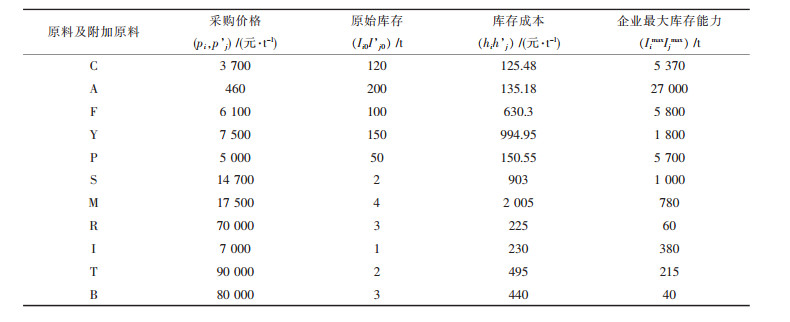
2 应用实例本文采用某铝企业生产数据对模型的有效性进行验证.该企业有3条电解线,2条浇铸线,其生产计划周期为月,十天一个计划时段,每个计划期分为三个计划时段,其中第一个计划时段的计划为执行计划,后两个时间段的计划为预计计划.每经过一个执行计划,根据执行计划的具体执行情况,原预计计划中的第一个时间段的计划作一定调整变成执行计划[16].相关生产数据见表 1~表 4.
| 表1 原料及附加原料数据 |
 |
| 点击放大 |
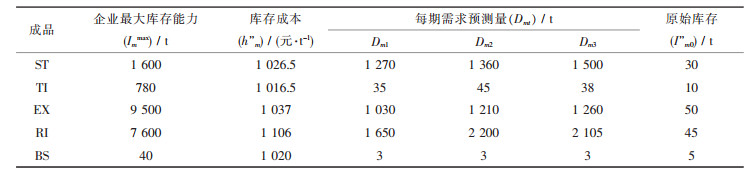
| 表2 最终产品数据 |
 |
| 点击放大 |
| 表3 电解生产线生产数据 |
 |
| 点击放大 |
| 表4 熔铸生产线生产数据 |
 |
| 点击放大 |
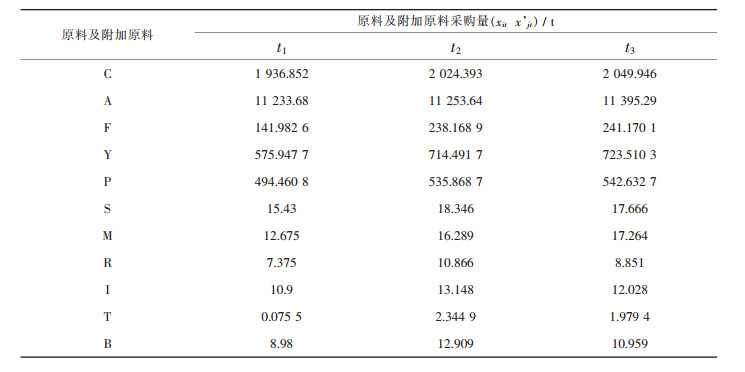
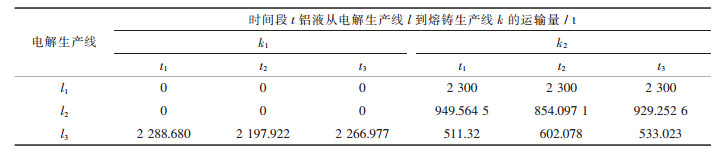
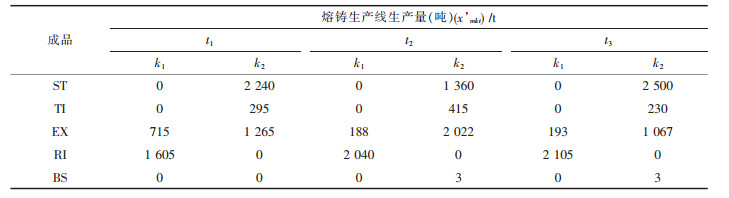
根据构建生产计划模型的特点及该企业计划问题的特性进行编程,采用lingo8.0进行求解,输入表 1至表 4中企业的实际数据,如原料及附加原料配比数据等,进过118次迭代后可得到全局最优解,求解结果见表 5~表 8.
| 表5 原料及附加原料采购量 |
 |
| 点击放大 |
| 表6 电解生产线生产量 |
 |
| 点击放大 |
| 表7 铝液从电解生产线到熔铸生产线的运输量 |
 |
| 点击放大 |
| 表8 熔铸生产线生产量 |
 |
| 点击放大 |
考虑到该模型规模较大,包含183个变量以及291个约束条件,对其进行灵敏度分析较难.本文通过观察模型中原材料及附加原料两类采购变量的变量系数值发现,因损耗量较小且采购价格较大,与原料不同的是,附加原料T采购量为非基变量,变量系数均值为90 360,对目标函数值影响较大,采购时应特别注意.比较三类库存(原料、附加原料、成品库存)变量可发现,原料A的变量系数值最小,原因来自于其库存成本小而消耗量大.对于松弛变量值(slack or surplus)的分析可验证,企业平均库存较小,远未饱和,鲜明对比的是电解线生产能力除l2外都饱和,而浇铸线则已接近2/3的生产能力.特别地,若忽略三条电解线生产成本间的差异、两条熔铸线间的生产成本差异以及电解线与熔铸线间的运输成本差异,计划方案相差很大,验证了计划制定时强调成本间差异的必要性.
从分析数据结果可发现,模型较好地满足生产实际的要求,能很好地计算出每个计划期具体时间段的资源采购量,每台设备的计划生产量、产品种类,改变了以往凭人工经验进行手工排产的混乱和低效[17].
3 结束语铝企业的生产计划问题应综合考虑其生产流程特点和内部物流特点,以及设备之间不同的生产能力和生产成本、铝液从电解生产线到熔铸生产线不同的运输成本等生产实际,因为这些差异使得不同的产品组合及设备安排会导致不同的生产成本.本文综合考虑原料采购到最终产品整个过程的物流形态及物流成本,从物流平衡的角度构建计划模型,运用实际生产数据对模型的有效性进行验证,验证数据结果显示,该计划模型符合生产实际状况,具有较好的实际应用价值.
| [1] |
A.C.Hax. Integration of strategic and tactical planning in the aluminum industry[J].
Operations Research Center M.I.T, Working Paper, 1973: 26–73. |
| [2] |
M.A.Hariga. A production planning model for an aluminum company[J].
King Sand Uiv, 1994(6): 241–264. |
| [3] |
Anantaram Balakrishnan. Process planning for aluminum tubes:An engineering-operations perspective[J].
Operations Research, 1996, 44(1): 7–20. DOI: 10.1287/opre.44.1.7. |
| [4] | 蒋美仙, 冯定忠, 陈勇, 等. 用网络计划技术优化企业生产计划问题[J]. 工业工程, 2003, 6(4): 48–52. |
| [5] | 彭频, 陈恩湖, 薛志全, 等. 铝企业生产调度问题的研究与应用[J]. 有色金属科学与工程, 2012(1): 23–26. |
| [6] | 陈建华, 彭鸿广. 基于时间竞争的MRPⅡ、JIT与TOC集成化生产计划与控制模型[J]. 工业工程, 2005, 8(2): 66–70. |
| [7] | 钱琼, 郑泽峰, 张安庭, 等. 生产计划问题的决策模型研究[J]. 计算机工程与应用, 2004(12): 220–223. |
| [8] |
M.R.Bowers, L.A.Kaplan, T.L.Hooker. A two-phase model for Planning the production of aluminum ingot[J].
Europen Journal of Operational Research, 1995, 81: 103–104. |
| [9] | 朱道飞, 王华, 马长波. 准时制下炼钢生产计划时间并行顺推编制方法[J]. 计算机工程与应用, 2010, 46(32): 236–240. |
| [10] | 王海凤, 彭加霖, 张茜. 基于约束满足的热轧无缝钢管生产计划模型与算法[J]. 计算机工程与应用, 2012, 15(21): 043–045. |
| [11] | 梁春华, 周泓, 夏晓雯. 采购与多层计划问题的协同优化[J]. 工业工程, 2011, 14(3): 29–33. |
| [12] |
Marc Gravel, Wilsonl Price, Caroline Gagne. Scheduling jobs in an Alcan aluminium foundry using a genetic algorithm[J].
INT. J. PROD. RES, 2000, 38(13): 3031–3041. DOI: 10.1080/00207540050117422. |
| [13] | 牟永善, 赵文波. 多品种中小批量类型企业生产计划控制方法的实证研究[J]. 现代制造工程, 2004(7): 98–101. |
| [14] | 胡琨元, 常春光, 郑秉霖, 等. 钢铁企业中库存匹配与生产计划联合优化模型与算法[J]. 信息与控制, 2004, 33(2): 177–180. |
| [15] |
Marc Gravel. Scheduling continuous casting of aluminum using a multiple objective ant colony optimization metaheuristic[J].
European Journal of Operational Research, 2002, 143: 218–229. DOI: 10.1016/S0377-2217(01)00329-0. |
| [16] | 王国磊, 钟诗胜, 林琳, 等. 递阶生产计划模式中综合计划层建模及求解[J]. 吉林大学学报:工学版, 2009, 39(5): 1202–1207. |
| [17] | 邵举平, 孙峰华, 黄宇. 钢铁企业面向物流的生产计划优化技术[J]. 冶金自动化, 2004(5): 14–17. |
 2013, Vol. 4
2013, Vol. 4

