| 3-RPC型并联精密定位机构设计与分析 |
近年来,随着微电子技术、通讯技术、航空航天技术、精密和超精密加工、生物工程、医学工程等技术的迅速发展,人们越来越迫切地需要具有微纳米级运动精度、多自由度、高度灵活的超精密定位系统,用于实现高精度的操作和实验研究[1].为了实现精密微动运动,研究人员对传统机械结构进行了大量的研究,如通常采用伺服电机和精密丝杠传动方案,然而这种定位方式由于螺纹间隙和传动摩擦的存在,必然存在定位误差使其定位精度降低,其运动精度一般只能达到微米级.为了补偿传动误差,提高分辨率,往往采用电磁或压电驱动对工作平台进行精细位置调整,但调整过程长、系统复杂,且由于空间耦合作用使得空间定位精度调整难以实现[2].因此,必须寻求特殊的驱动和传动方式以及高精度的控制方法以使平面工作台具有亚微米,甚至纳米级的位移分辨率.柔顺并联机构的出现为实现更高精度的微纳米级定位的机构设计提供了新的、更彻底的方法.
柔顺并联机构是一种具有复杂结构的柔性机构, 它不像传统刚性机构那样靠运动副来实现全部运动和功能而主要靠机构中的柔性构件或机构本身的柔性来实现机构的主要运动和功能,以实现运动、力、能量和位移的传递和转换[3].一般柔顺机构通过利用柔性铰链来代替对应的相关传统铰链,利用柔性铰链受力时的弹性变形传递力和运动,达到整个柔性支链的输出运动.由于柔顺机构由弹性元件构成,进行替代后可能导致机构整体刚度降低,继而出现了全柔顺并联机构,即在整体弹性材料上经线切割加工出全柔顺支链进而集成为全柔顺并联机构.具有全柔顺支链特点的并联机构和传统机构相比有以下优点:①全柔顺支链经整体线切割加工,免于装配;②无间隙和摩擦;③免于润滑;④可设计为整体式提高全柔顺并联机构整体刚度[4-5].基于全柔顺机构上述优点,使得其在精密微动定位领域有着较好的应用前景.
本文设计出一种具有全柔顺支链的空间三自由度RPC型并联机构.首先应用螺旋理论对空间3-RPC型并联机构构型进行了分析,对机构自由度及空间几何约束条件进行了分析.运用拓扑优化设计出RPC型全柔顺支链,进而集成为全柔顺并联机构.在Solidworks软件中建立了空间3-RPC型全柔顺并联机构模型并利用ANSYS有限元分析软件对机构的微定位情况进行了仿真验证.
1 3-RPC型并联机构构型分析 1.1 螺旋理论将机构的转动副表示为螺旋:
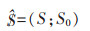
|
(1) |
将机构的移动副表示为螺旋:
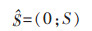
|
(2) |
其中,S是运动副轴线的单位矢量,S0=r×S是直线的线矩,等于从原点到该轴线的矢径r与S的叉乘积[6-7].机构中所有螺旋构成螺旋系,在三维空间线性无关的螺旋数目为6,当所研究的螺旋系线性无关的螺旋数n等于6时,不存在反螺旋;当螺旋系的线性无关螺旋数n小于6时,存在6-n个反螺旋,与所有运动螺旋相逆,使反螺旋与运动螺旋互易积为零.
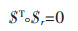
|
(3) |
其中,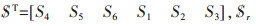
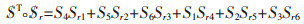
3-RPC并联机构是由皆为等边三角形的上、下平台及连接两平台的3条支链组成,如图 1所示.其中下平台为固定平台,上平台为运动平台,3条支链结构相同,均为RPC支链.每条支链与固定平台相连的运动副为转动副R,与运动平台相连的运动副为圆柱副C,在转动副与圆柱副之间为移动副P,以3个移动副P作为机构的驱动副.每条支链中R副轴线与C副轴线平行,P副轴线与R副和C副轴线相交.
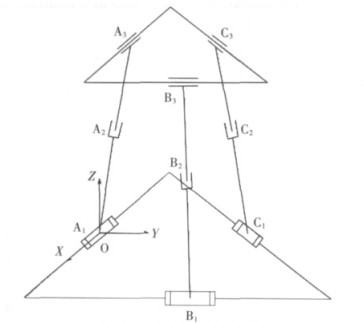 |
| 图 1 3-RPC并联机构 |
以转动副A1中心为原点,建立直角坐标系o-xyz,根据螺旋理论可知,支链A1A2A3的运动螺旋为:

|
其中,b2、c2、b3、c3的值由并联机构运动过程中支链A1A2A3中P副和C副的的空间位置所确定.
根据螺旋理论中运动螺旋和约束螺旋的互易积为零,由式(3)可求出支链A1A2A3的反螺旋为:

|
由求得支链的反螺旋可知,动平台沿y’、z’轴方向均受到两个约束力偶的作用,限制了动平台绕y’、z’轴方向的两个转动自由度,又由于3条支链呈120 °对称分布,可知3条支链对运动平台限制了绕x’、y’、z’方向的转动,机构约束力偶如图 2所示.因此,动平台具有沿x’、y’、z’方向的3个移动自由度,所以,3-RPC并联机构是一种具有三维平动的并联机构.
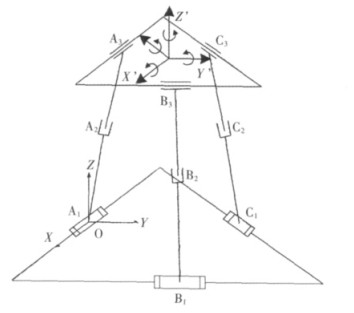 |
| 图 2 3-RPC并联机构约束力偶 |
前面基于并联机构学中的螺旋理论,对3-RPC型并联机构自由度进行了分析,同时可得出满足机构空间三平移运动各运动副轴线所需满足的空间几何约束条件.圆柱副A3、B3、C3可分别分解为一个转动副和一个移动副,且分解形成的转动副轴线与移动副轴线方向一致,分解形成的各转动副轴线之间的夹角为60°.每条运动支链中转动副A1、B1、C1轴线分别与同一支链中圆柱副A3、B3、C3所分解的转动副轴线平行.机构几何约束螺旋表示如图 3所示.
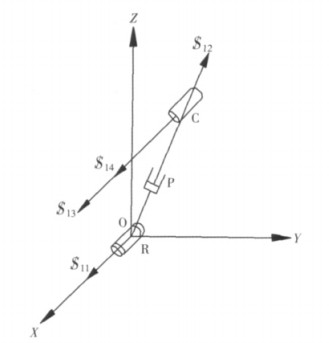 |
| 图 3 RPC支链运动螺旋 |
2 基于拓扑优化理论的全柔顺并联机构设计
拓扑优化在结构优化中是最高层次的,而且是最综合的[8].机械结构的优化可根据许多准则来定义,可以按具有最大刚度、最小重量、最大强度、适当的柔性、最大的抗冲击力等适当的动力学特性以及其他许多目标函数来对机械结构进行优化[9-10].柔顺机构利用机构本身弹性元件的弹性变形来传递力和运动,因此,在设计中要求机构有足够的柔性,同时为了使得机构能够承受较大载荷,必须使机构具有足够的刚度以防止柔顺机构的失效.当柔顺机构满足设计要求并且只想用有限的材料来制作机构时,可对柔顺机构进行拓扑优化从而在满足设计要求的同时大大降低材料成本.
2.1 连续材料密度参数化法连续材料密度参数化方法是在设计域内定义每个实体单元的相对密度.定义单元i(i=1,2,3,…)的密度变量为ρi,此单元的有效杨氏模量可由式(4)给出:
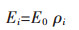
|
(4) |
其中,E0是该材料的实际杨氏模量.当ρi值较小达到下界时,表示该单元是由很软的材料构成,因此可以把该单元从结构中虚拟分离出来.如果一组连续相邻的单元都达到下界,材料就会出现孔状结构.如果ρi达到上界,表示该单元是柔顺机构最优化不可缺少的实体部分.如果ρi在上下界之间,表示为柔顺机构优化中的过渡区域.
2.2 参数化模型的建立设目标函数f(x1,x2,…,xn),p个等式约束和m个不等式约束,n个设计变量(x1,x2,…,xn).一般约束的优化问题可描述为寻求设计变量的最优值,以使目标函数在满足等式和不等式条件下为最小值.
Minimize:f(x1,x2,…,xn)
Subject to:
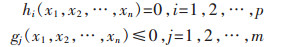
|
约束优化问题的必要条件即Karush-Kuhn-Tucher条件,可表示为:
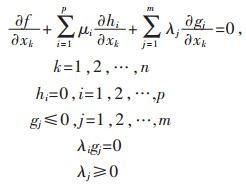
|
解以上方程和不等式可得n个变量,承子μi(i=1,2,…,p)和λj(j=1,2,…,m)的最优值.得到的承子叫做Lagrange承子.用这些承子作为附加未知量,通过定义Lagrangian函数,继而将约束问题转化为无约束问题:
Minnimize
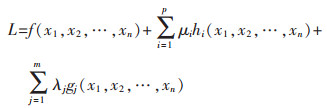
|
全柔顺并联机构拓扑优化设计中,考虑机构刚度、柔度作为目标函数.即在设计机构时使其在柔度满足条件的情况下用有限材料制造机构,并能够使机构刚度最大化的材料分配方案[11].考虑柔顺并联机构的空间几何约束条件的优化问题模型可表示为:
Minimize:
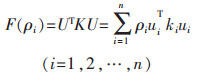
|
(5) |
Subject to:
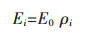
|
(6) |
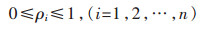
|
(7) |
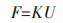
|
(8) |
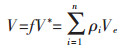
|
(9) |
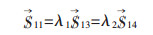
|
(10) |
其中,ρi为设计变量,U为机构整体位移,K为机构整体刚度矩阵,ui和ki分别为单元位移向量和刚度矩阵,Ei为单元的有效杨氏模量,E0为材料的实际杨氏模量,V为实际材料用量,f为设定的材料用量百分比,V*为设计域内的材料总量,Ve为单元材料体积,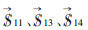
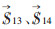
设计出的RPC型全柔顺支链如图 4所示,其中,1为固定支链的螺栓孔,2为安装压电陶瓷驱动器的定位槽,安装压电陶瓷驱动器并以移动副P1作为驱动副,圆柱副C由转动副R3及移动副P2组成,为使得RPC全柔顺支链达到较好的运动特性,设计一组关于移动副P1对称的转动副R1和R2共同完成支链转动副的功能.
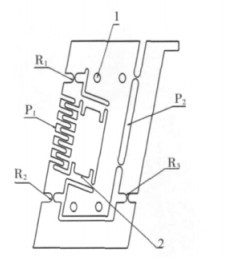 |
| 图 4 RPC型全柔顺支链 |
3-RPC型全柔顺并联机构如图 5所示,机构由3个RPC型全柔顺支链集合而成,各支链间通过夹角120°分别固定在支撑板上进而固定在固定平台上,各全柔顺支链终端与机构动平台相连.
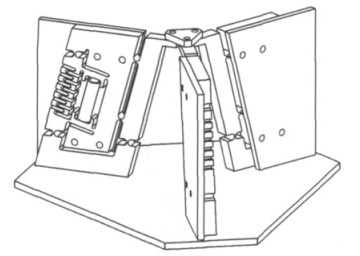 |
| 图 5 3-RPC型全柔顺并联机构 |
3 基于有限元的全柔顺并联精密定位机构仿真验证
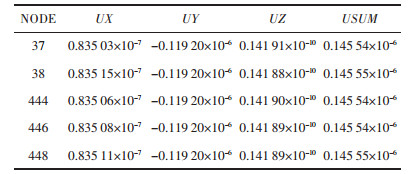
在Solidworks软件中建立RPC型全柔顺并联机构三维实体模型并将其转换为Ansys有限元软件可识别的Parasolid型文件,进而导入Ansys软件进行静力学分析[12-13].在Ansys分析时选择线性同性材料,材料选择65Mn弹簧钢,弹性模量为207 GPa,泊松比为0.3,密度为7 850 kg/m3,采用智能网格划分对实体单元进行网格划分.RPC型全柔顺支链以移动副P副作为驱动副,在施加载荷时约束4个固定螺栓孔的所有自由度,并在压电陶瓷驱动器处施加500 N的驱动力.全柔顺支链网格划分如图 6所示,位移变形云图如图 7所示,全柔顺支链应力云图如图 8所示.全柔顺支链与运动平台相连接的输出端关键节点位移数据如表 1所示.
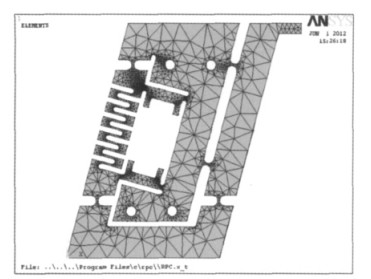 |
| 图 6 RPC型全柔顺支链网格划分 |
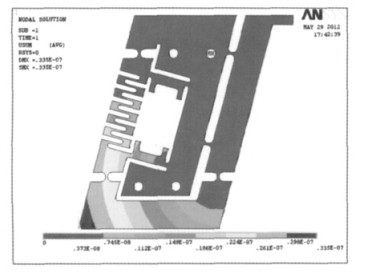 |
| 图 7 RPC型全柔顺支链位移云图 |
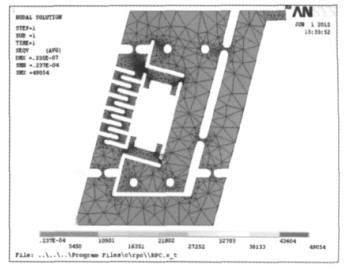 |
| 图 8 RPC型全柔顺支链应力云图 |
| 表1 RPC型全柔顺支链输出端关键节点位移数据/mm |
 |
| 点击放大 |
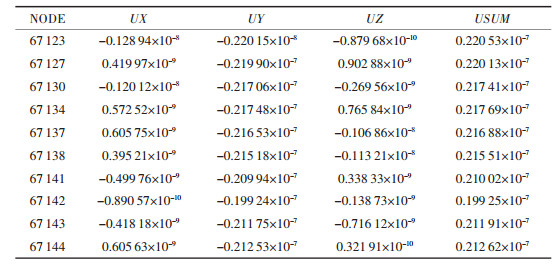
将设计出的全柔顺并联机构导入ANSYS软件进行分析,对机构每条支链中的4个定位螺栓孔施加约束,约束其全部自由度,并分别在图 4所示2处施加压力载荷500 N,对输入参数进行仿真分析,得出机构位移变形云图如图 9所示,机构应力等值线云图如图 10所示.选择机构输出终端关键节点,各节点位移如表 2所示.
 |
| 图 9 RPC全柔顺机构位移变形云图 |
 |
| 图 10 RPC全柔顺并联机构应力云图 |
| 表2 RPC型全柔顺机构输出端关键节点位移数据/mm |
 |
| 点击放大 |
4 结束语
基于并联机构学及柔顺机构学理论,运用拓扑优化原理设计出一种新型空间三自由度型3-RPC全柔顺并联机构应用于精密定位.对3-RPC型并联机构构型及其自由度进行了分析,并求解出其反螺旋,分析了该机构空间几何约束条件.基于拓扑优化理论建立了该全柔顺并联机构参数化模型,设计出一种新型柔顺机构并建立了该机构三维实体模型.在ANSYS有限元分析软件中对所设计的全柔顺机构进行了静力学分析,分别得出全柔顺支链及整体结构的位移云图、应力云图和关键节点位移数据.通过仿真结果可知,驱动机构运行时其位移及应力分布合理,终端动平台能够达到微纳米级定位精度要求,验证了该设计的可行性和有效性.
| [1] |
Choi Y J, Sreenivasan S V, Choi B J. Kinematic design of large displacement precision XY positioning stage by using cross strip flexure joints and over-constrained mechanism[J].
Mechanism and Machine Theory, 2008, 43: 724–737. DOI: 10.1016/j.mechmachtheory.2007.05.009. |
| [2] |
Chen G, Howell L L. Two general solutions of torsional compliance for variable rectangular cross-section hingesin compliant mechanisms[J].
Precision Engineering, 2009, 33(3): 268–274. DOI: 10.1016/j.precisioneng.2008.08.001. |
| [3] | Larry L, Howell. Compliant mechanisms[M]. New York: John Wiley and Sons , 2001. |
| [4] | 张宪民. 柔顺机构拓扑优化设计[J]. 机械工程学报, 2009, 45(1): 180–187. |
| [5] | 张连杰, 刘善增, 朱真才. 柔顺机构的研究进展[J]. 组合机床与自动化加工技术, 2011(7): 108–112. |
| [6] | 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社 , 2006: 5. |
| [7] | 朱大昌, 严智敏. 3-RPS并联机器人位置分析及控制仿真[J]. 有色金属科学与工程, 2012, 3(1): 95–100. |
| [8] | 占金清, 张宪民. 基于基础结构法的柔顺机构可靠性拓扑优化[J]. 机械工程学报, 2010, 46(13): 42–47. |
| [9] | 占金青.基于基础结构法的柔顺机构拓扑优化设计研究[D].广州:华南理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10561-2010229199.htm |
| [10] |
Henry Panganiban, Gangwon Jang, Taejin Chung. Topopogy optimization of pressure-actuated compliant mechanisms[J].
Finite Elements in Analysis and Design, 2010, 46(3): 238–246. DOI: 10.1016/j.finel.2009.09.005. |
| [11] |
Rubio W M, Nishiwaki S, Silva E C N. Design of compliant mechanisms considering thermal effect compensation and topology optimization[J].
Finite Elements in Analysis and Design, 2010, 46(12): 1049–1060. DOI: 10.1016/j.finel.2010.06.010. |
| [12] | 杨春辉, 刘平安. 整体弹性关节平面并联微动机器人ANSYS有限元分析[J]. 机械设计与制造, 2007(3): 73–75. |
| [13] | 未永飞, 闫国华, 冯利法, 等. 基于ANSYS的蒸汽发生器机械堵管接触分析[J]. 机械设计与制造, 2012(4): 106–108. |
 2012, Vol. 3
2012, Vol. 3

