| 某铜矿逆断层对围岩稳定性影响数值分析 |
我国国土广袤,各地地质构造复杂多变,岩层中节理裂隙发育,存在着大量连续或不连续结构面、断层、泥化夹层,许多矿产资源都赋存在断裂破碎带附近,甚至处于断裂破碎带之中.由于断裂破碎带附近的地质构造应力复杂,岩层不同程度的破坏对地下开采工作面影响极大,断裂破碎带附近由于开采扰动引起的应力变化难以预料.目前,数值模拟被广泛地用于研究地下工程开挖所引起的地应力变化,但是我们在建模的时候为了便于计算一般会采取简化模型的方法,在不影响研究结果的情况下选择性地将一些次要因素忽略.本文以某铜矿为例分析双逆断层破碎带对采场围岩稳定性的影响,得出双逆断层破碎带对围岩稳定性影响的规律.为下一步研究提供指导.
1 工程地质状况某铜矿矿区的基本构造是一个被断裂破碎带所破坏了的单斜构造,该矿的Ⅴ号矿体为区内规模最大的原生硫化铜矿体,Ⅴ号矿体位于矿区中部,受F1和F3两条逆断层破碎带的控制.矿体倾角一般为40°~45°,最大厚度62.58 m,一般厚10~30 m,平均厚度14.69 m.矿体围岩以细砂岩和粉砂岩居多.
矿体的直接顶板为石炭系壶天群硅化破碎砂岩、碳酸盐岩类,岩石经过硅化胶结后具有硬、脆、碎的性质,抗压强度为100 MPa左右.矿体底板为石炭系梓山组泥质页岩、炭质页岩、砂质页岩和黏土岩等,易吸水膨胀、松散,稳定性差,抗压强度60 MPa左右.
Ⅴ号矿体以原生黄铜黄铁矿为主,胶状黄铁矿和黄铁矿次之.黄铜黄铁矿石中的裂隙不发育,岩体完整性好,稳定性好,抗压强度约为180 MPa.
逆断层破碎带分别位于矿体上盘、下盘,紧贴矿体,将矿体夹在中间,宽度10~20 m;倾角30°~50°.断层的裂隙普遍发育,密度大,岩石被切成块状,其小块岩样强度虽大,但岩体稳定性却较差,属于不稳定类岩层.断层破碎带,特别是断层交叉处,岩体的稳定性极差,属于最不稳定类岩层.
2 数值模型的建立及赋值 2.1 模型建立为便于计算,采用忽略一些模型次要影响因素的方法,根据原矿体的几何形状以及埋藏条件将模型简化为规则的几何形状,建立研究模型,简化后的模型对研究结果影响不大,符合要求.模型在ANSYS中建立,并划分网格,然后用转化软件导入FLAC3D中进行计算分析[1].模型中X轴方向平行矿体走向,Y轴方向垂直矿体走向,Z轴为模型标高[2],建立了两个模型进行对比分析.其中模型1(图 1)为未考虑断层的情况,包括上盘围岩、矿体和下盘围岩;模型2(图 2)是考虑断层的情况,包括上盘围岩、下盘围岩、上盘断层破碎带、下盘断层破碎带以及矿体.整体模型的尺寸为300 m×200 m×200 m(X×Y×Z),模型顶部到地表的距离为150 m.矿体厚度取30 m,倾角取45 °,模型2上下盘断层破碎带厚度均取10 m;断层倾角取45 °.开挖工程的几何参数根据该铜矿的采矿方法可知,矿房几何参数为10 m×10 m×30 m,矿柱宽度为4 m.通过比较两个模型开挖前后围岩应力应变情况来分析逆断层的影响.
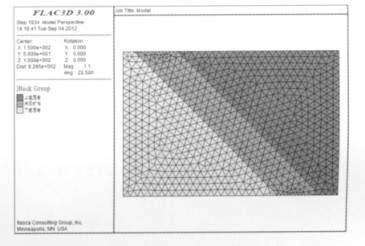 |
| 图 1 整体模型(模型1) |
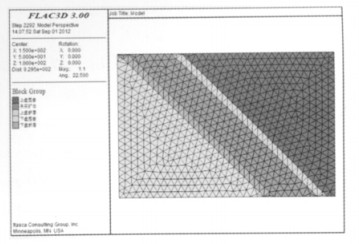 |
| 图 2 整体模型(模型2) |
2.2 模型赋值
模型建成后对模型进行赋值,模型的岩体物理力学参数主要有体积模量、切变模量、抗拉强度、内聚力、内摩擦角、容重和泊松比等,这些参数是在实验室获取的,为获得与现场实际相近的岩体物理力学参数,可采用多种方法对获得的岩石力学参数进行处理,本模型采用Mitri在RMR值基础上提出的折减因子计算公式:

|
(1) |
其中:Rf为折减因子;Eint为岩块弹性模量;Erm为岩体弹性模量.
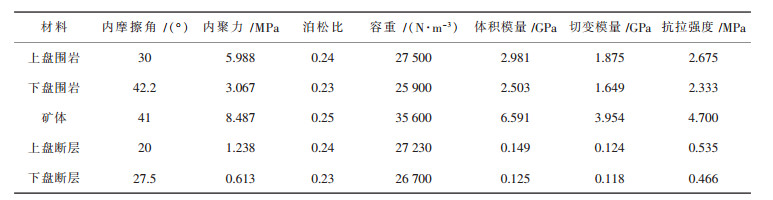
通过式(1)可求得模型岩体强度参数折减因子,并在此基础上,求得围岩体的物理力学参数,结果见表 1.而断层带的物理力学参数,采用弱化断层内介质的方法获得,该铜矿两逆断层岩体组成上盘主要为粉砂岩,下盘为页岩,并都伴有夹泥.因此,将两逆断层带分别看作是由粉砂岩或页岩组成的岩体,其物理力学性质就以弱化粉砂岩或页岩力学参数的方式给定,即在得到的围岩体物理力学参数基础上再次折减[3-5].宋晓梅、田彩霞等对岩体物理力学参数修正的研究表明:在数值计算模型所需的所有物理力学参数中,岩体的弹性模量对计算结果影响最大.完整性越差,弹性模量越小,岩体的弹性模量一般为岩块的1/7~1/20[4].所以,断层破碎带物理力学参数选择的主要任务是给定合理的弹性模量[4].为了凸显出软弱结构面的影响作用,将弹性模量折减系数定为1/20,转换成体积模量折减系数是1/20,切变模量折减系数定为1/15.其他参数是通过与该铜矿断层性质相似的大量断层类比而给定的.计算模型材料物理力学参数如表 1.
| 表1 计算模型材料力学参数 |
 |
| 点击放大 |
3 数值模拟分析 3.1 初始应力场
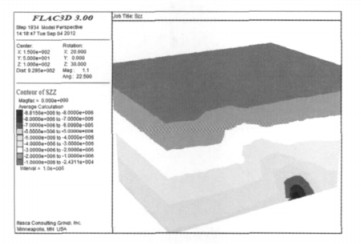 |
| 图 3 初始应力场(模型1) |
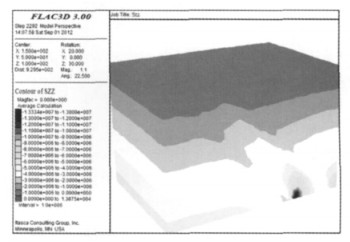 |
| 图 4 初始应力场(模型2) |
图 3~图 4是两个模型只考虑重力场作用的初始应力场,从图 3可以看出模型1的初始应力分布呈现层状的由浅到深逐步增大的特点,在模型中部沿矿体倾斜的方向,应力分布虽也符合由浅到深逐步增加的规律,但是该区域应力大小普遍高于同水平围岩,并在最深处有应力集中的现象,原因是矿体的容重比围岩大,所以受到的重力影响更大;从图 4可知,模型2整体应力分布与模型1一致,但由于受到逆断层的影响有少许变化,即在断层存在的区域应力曲线向下凹,初始应力小于同水平的围岩以及矿体,原因同样是容重小,同时,模型2最深处也出现应力集中的现象,但是受到断层的影响,应力分布紊乱、复杂.图 3~图 4说明建立的模型是合理的,材料赋值是可靠的.
3.2 最大主应力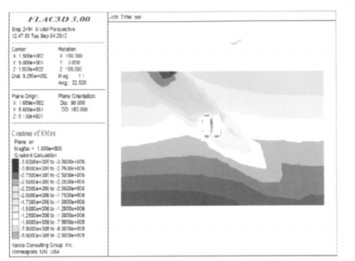 |
| 图 5 最大主应力(模型1) |
 |
| 图 6 最大主应力(模型2) |
图 5~图 6是模型最大主应力的分布图,图 5中,该区域最大主应力自地表向下大致呈层状分布,且逐渐增大,在矿体赋存的区域最大主应力沿矿体倾向的方向相对于同水平围岩减小,在开挖矿房的顶板、底板以及矿柱均出现应力集中,最大达到2.5 MPa,低于矿体破坏极限,是稳固的;从图 6可以看到模型2最大主应力在矿体上盘分布紊乱,大小并不随着深度的增加而增大[6],在矿房正上方的模型顶部区域出现应力集中,其他大部区域也出现应力增加,深部应力减小,而在矿体下盘最大主应力的分布则呈现如模型1的规律性分布,说明矿房开挖对上盘围岩最大主应力分布影响巨大,而对下盘围岩影响很小,可以忽略不计[7].
3.3 剪应力 |
| 图 7 最大剪应力(模型1) |
 |
| 图 8 最大剪应力(模型2) |
由图 7~图 8可知,从两个模型的整体来看,在沿矿体赋存区域最大剪应力明显高于上下盘围岩,模型2相较模型1最大剪应力分布主要在矿体下盘有较大改变,模型2围岩整体应力大小有所增加.同时,从图 7中可以看出,模型1在开挖矿房处四个角出现相对应力集中,呈对称分布,最大剪应力达到2.25 MPa[8];而图 8中,模型2只在最靠近下盘逆断层的矿房角落处出现应力集中,最大剪应力达到3.5 MPa[8],矿房其他易引起应力集中的拐角处没有出现应力集中,说明逆断层使最大剪应力的分布复杂化,改变了应力集中出现的区域,这可能会造成意外事故.
3.4 塑性区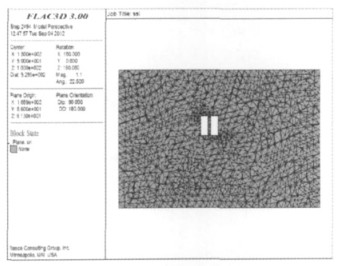 |
| 图 9 塑性区(模型1) |
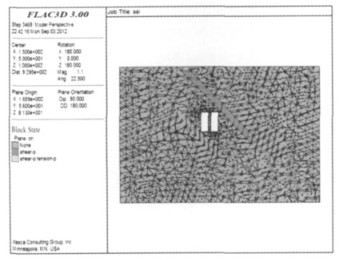 |
| 图 10 塑性区(模型2) |
地下工程的开挖,会打破原岩应力平衡,从而导致应力重新分布[9].当岩体所受的拉应力大于自身的抗拉强度时,就会导致岩体发生拉伸破坏[10];当岩体所受的剪应力大于自身的抗剪强度时,就会导致岩体发生剪切破坏[11];这些现象在数值模拟中都以塑性区的形式表现出来,塑性区是判断采空区稳定与否的重要标准.
由图 9可知,模型1在矿房开挖后,在整个模型中均未出现塑性区,这说明矿房开挖引起的围岩拉应力或剪应力小于岩体的抗拉强度或抗剪强度[12],岩体应力重新达到平衡,采空区是稳定的;图 10中,我们看到,只在上盘围岩出现了严重的剪切破坏塑性区,从模型顶部一直延伸到开采平面以下,其所在的区域正好是上盘断层的位置,说明上盘断层失稳,这给空区顶板的稳定性造成巨大的压力,顶板可能出现冒落、片帮甚至垮塌,在实际生产中就出现过顶板垮塌的事故,幸好未造成人员伤亡,但这恰好证明了本文所建模型是合理的,研究结果是正确的.
3.5 位移为了监测矿房开挖导致的顶板位移,设置了3个监测点2#、3#、4#,其中2#是左边矿房顶板中心点,3#是右边矿房的顶板中心点,4#号监测点在矿柱的中点.矿房开挖后,监测点的位移变化曲线如图 11~图 12所示.
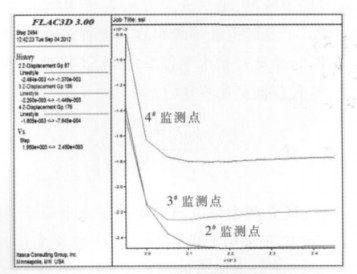 |
| 图 11 监测点位移(模型1) |
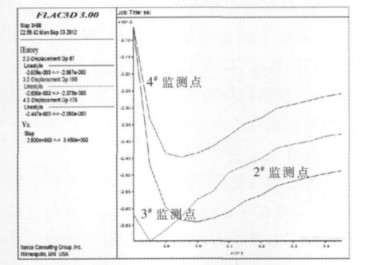 |
| 图 12 监测点位移(模型2) |
由图 11~图 12可知,各监测点的位移均发生沉降,具体表现为:随着矿房的开挖,各监测点均出现不同程度的沉降,其中,模型1各监测点位移沉降分别为2#为2.4 cm、3#为2.2 cm、4#为2.0 cm,沉降均未超过2.4 cm,而模型2各监测点位移沉降分别为2#为2.65 cm、3#为2.7 cm、4#为2.45 cm,位移沉降明显增大,其原因在于断层破碎带属软弱岩层,对上覆岩层压力未形成足够的支撑力,导致上覆岩层压力向下传导,引起顶板位移沉降增大,严重的可能导致顶板冒落甚至垮塌.
3.6 结果通过对模型1和模型2的初始应力场、最大主应力、最大剪应力、塑性区、位移监测点的对比分析,可以得出:断层破碎带改变了围岩的初始应力场分布规律,使深部围岩初始应力分布更加复杂[13];改变了最大主应力的似层状分布,增大了上盘围岩的最大主应力,减缓了矿房顶板的应力集中现象;改变了最大剪应力的分布规律[14];使上下盘围岩的剪应力都有所增加,在矿体上盘出现大片应力集中区域,最大剪应力从2.25 MPa增大到3.5 MPa;上盘断层破碎带出现大面积的剪切破坏塑性区,延伸至开挖水平以下;加大了顶板位移沉降量,导致顶板更加不稳定.
4 结论通过建立两个数值模型模拟了处于两条逆断层中的矿体开采引起的围岩应力、位移变化,得出:逆断层改变了围岩的初始应力、最大主应力、最大剪应力分布规律,增大了围岩部分区域的最大主应力和最大剪应力[15],尤其是矿体上盘的围岩应力,改变了围岩应力集中区域,导致上盘断层出现剪切破坏区,增大了顶板的沉降,导致顶板不稳定,出现冒落垮塌的现象需引起重视,这为该矿山顶板处理提供了预警,同时对相似矿山有一定的参考价值.
当然因为当前研究的技术条件以及作者能力有限,本文存在一定的不足之处,其中如何使模型贴合实际,断层参数的确定更加科学有待于进一步研究.
| [1] | 夏菲菲. 洪屏地下厂房围岩稳定性分析[J]. 水科学与工程技术, 2007(1): 44–46. |
| [2] | 李想, 吕玲芝, 谢晓斌. FLAC-3D在圈定地表移动带中的应用[J]. 有色金属科学与工程, 2011, 2(2): 76–80. |
| [3] | 张宏伟, 张文军, 李胜. 断裂应力场模拟分析与应用[J]. 湘潭矿业学院学报, 2002, 17(2): 1–3. |
| [4] | 李兴, 李庆倩, 贺可强. 高阳铁矿导水断层预注浆设计数值模拟研究[J]. 现代矿业, 2009, 9(9): 67–72. |
| [5] | 林宗元. 岩土工程试验监测手册[M]. 沈阳: 辽宁科学技术出版社 , 1994. |
| [6] | 宋远兵. 公路下磷矿开采采场结构参数的数值计算优选[J]. 现代矿业, 2011(3): 4–5. |
| [7] | 陈梅芳, 丁德馨. 简易位移报警器在膨胀性软岩巷道支护中的应用[J]. 采矿技术, 2006(3): 331–333. |
| [8] | 宋卫东, 杜建华, 匡忠祥, 等. 露天转地下开采巷道围岩应力场变化规律研究[J]. 中国矿业, 2005(3): 52–56. |
| [9] | 楼旭东, 吴金荣. 喷锚支护对硐室围岩稳定性的影响浅析[J]. 江苏冶金, 2004(2): 44–46. |
| [10] | 陈明卢, 文波, 周创兵, 等. 初始地应力对隧洞开挖爆生裂隙区的影响研究[J]. 岩土力学, 2009(8): 2254–2258. |
| [11] | 郑瑞宏. 关于土体中任意一点所处状态的判断与分析[J]. 科技创新导报, 2008(5): 192. |
| [12] | 崔中兴, 宋克强. 隧洞围岩破坏准则的研究[J]. 西北水资源与水工程, 1994(1): 7–13. |
| [13] | 李波.忻保高速公路芦芽山隧道断层破碎带围岩稳定性分析[D].西安:长安大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-11941-1011185249.htm |
| [14] | 刘红平. 沥青面层层间剪应力的影响因素分析[J]. 山西建筑, 2010(12): 268–269. |
| [15] | 陆山风. 爆破振动作用下小净距隧道围岩的力学行为分析[J]. 中国科技纵横, 2010(15): 446–447. |
 2012, Vol. 3
2012, Vol. 3

