有色金属科学与工程  2012, Vol. 3 Issue (3): 10-14
文章快速检索     高级检索
引用本文
0
辛波, 佟志芳, 谢森林, 陈涛. 五流连铸中间包结构优化的水模型实验[J]. 有色金属科学与工程, 2012, 3(3): 10-14. DOI:10.13264/j.cnki.ysjskx.2012.03.017.
XIN Bo, TONG Zhi-fang, XIE Sen-lin, CHEN Tao. Water modeling experiment on structure optimization of five-strand continuous casting tundish[J]. Nonferrous Metals Science and Engineering, 2012, 3(3): 10-14.DOI: 10.13264/j.cnki.ysjskx.2012.03.017.
五流连铸中间包结构优化的水模型实验[PDF全文]
辛波1,2, 佟志芳1 , 谢森林1, 陈涛1    
1. 江西理工大学冶金与化学工程学院，江西赣州341000;
2. 方大特钢科技股份有限公司， 南昌330000
基金项目：国家自然科学基金资助项目（50974064）
通信作者：佟志芳(1972- ),男,博士,教授,主要从事冶金二次资源综合利用研究,E-mail:tongzhifang1998@126.com
作者简介： 辛波(1977- ),男,工程师,主要从事连铸生产工艺优化方面研究,E-mial:71657844@qq.com
收稿日期：2012-03-03
摘要：以国内某钢厂五流连铸中间包为研究对象，根据相似原理建立了1∶3 的中间包水模拟系统，考察不同内部结构对中间包流体流动特性的影响.研究结果表明：原型中间包内部结构不合理，各流水口之间的流体流动特性差异很大，存在较大死区.通过内部结构优化设计，使中间包流场得到明显改善，其中方案Ⅵ效果最佳，平均停留时间离散度最小，活塞区体积达23.84 %，死区体积为10 %，比原型下降了71.70 %.
关键词： 连铸    中间包    水模型    结构优化    
Water modeling experiment on structure optimization of five-strand continuous casting tundish
XIN Bo1,2, TONG Zhi-fang1 , XIE Sen-lin1, CHEN Tao1    
1. School of Metallurgy and Chemical Engineering, Jiangxi University of Science and Technology , Ganzhou 341000, China;
2. Fangda Special Steel Science and Technology Co. Ltd., Nanchang 330000, China
Abstract: Based on the five-strand caster tundish in a domestic steel plant，water modeling system with the 1 : 3 similarity ratio is set up to study the effect of the different internal structure on fluid flow characteristics of tundish according to the similar principle. The results show that the unreasonable internal structure of prototype tundish and different flow characteristics between outlets with large dead zone volume and unfavorable mixing effect. The field characteristics of tundish are improved remarkably by optimizing the internal structure design. Of which, the scheme VI enjoys the optimal mixing effects for its minimum dispersion degree of mean residence time. The plug volume amounts to 23.84 % with dead zone volume of 10 %, which is decreased by 71.70 ％ compared to the prototype tundish．
Key words: continuous casting    tundish    water model    structure optimization    
0 引言

连铸中间包是钢包与结晶器之间重要的连接设备，它具有储存、分配钢液和实现多炉连浇的作用，可以促使钢液中夹杂物的上浮与分离、均匀钢水温度，进而提高铸坯质量，保证连铸生产顺行[1].中间包内部结构、控流装置布置合理与否，直接影响中间包内钢液的流动状态，从而影响钢液内夹杂物的去除.近年来，国内外关于中间包冶金进行了大量的学术研究.左祥均[2]通过采用合适的湍流抑制器，最小停留时间增加30 %～50 %，峰值时间增加40 %～70 %.段善勇[3]研究发现，挡墙设置对包内钢液的流动有非常重要的影响.张体广[4]设置合理的控流装置，各流之间的RTD 曲线趋于一致，活塞流体积大大增加，死区体积下降38 %.彭琦[5]采用优化设计的控流装置，中间包死区体积仅为5.6 %.

国内某钢厂现有的五流连铸机中间包，由于没有采用任何控流装置，钢水在包内各水口的分配非常不均.远端水口钢水流动时间长，温降较大，近端水口钢水温度高，流程短，钢液中夹杂物来不及上浮就进入结晶器中，导致铸坯质量差，难以满足品种钢生产的需要，因此，对中间包内部结构进行优化具有非常实际的意义.实践证明，利用水模型对中间包进行物理模拟是寻找合理、有效的控流元件，优化中间包内钢水流场的较为直观和有效的方法[6-15].本研究采用水模型物理模拟方法对中间包内流场进行了研究，通过研究优化了中间包内的流场，并确定了合理的控流装置，促进连铸生产顺行和铸坯质量的提高.

1 实验原理与方法 1.1 实验原理

中间包内钢液的流动，一般可视为黏性不可压缩稳态流动，流动的驱动力主要是重力和惯性力.同时，中间包内钢液流动与模型中水的流动处于同一自模化区.根据相似原理，只需保证两个系统间弗鲁德准数相等，就可以保证模型和原型的相似[16].由弗鲁德Fr 准数相等确定的模型与实型中流体的速度、流量、平均停留时间间的关系如下：

(1)
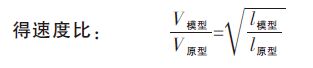
(2)
(3)
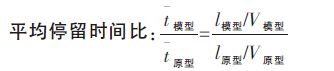
(4)

其中，g 为重力加速度，9.8 m/s2；l 为特征长度，m； V为流体速度，m/s； Q 为流体流量，m3； t軃为流体平均停留时间，min.

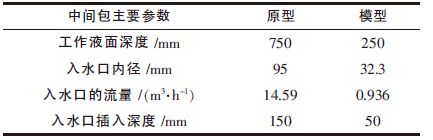
本实验选用模型：原型为1∶3 的缩小比例来建立物理模型，经计算，得到的中间包原型及模型的主要技术参数见表 1，其中入水口的流量根据铸坯拉速（1.9 m/min）通过质量守恒定律计算得出.

表1 中间包模型与原型主要参数表
点击放大

1.2 实验方法

实验用自来水模拟钢液，透明有机玻璃作为中间包的制作材料，用泡沫板制作挡墙.采用刺激-响应技术，考虑到中间包的对性称，实验中只考察中间流（1 流）、右侧的两流（2 流、3 流），以饱和NaCl 水溶液作为示踪剂，测量中间包1、2、3 流水口出口处流体的电导率变化，通过对采集到的数据进行处理得到停留时间分布曲线（RTD 曲线），分析中间包内流体的流动特性[17].采用标准差来考察各流的分散程度：

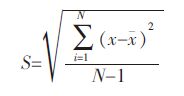
(5)

其中：S 为标准差；xi为第i 个样本值，i=1，2，3； x为表示样本的算术平均值；N 为样本个数，N=3.

对于五流中间包来说，所考察参数的S 值越小，说明参数的离散程度也越小，五流的流动特性越接近.中间包原包结构示意图如图 1 所示.实验装置示意图如图 2 所示.

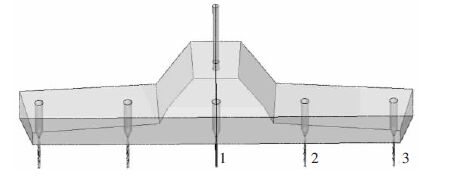图 1 中间包原包结构示意图

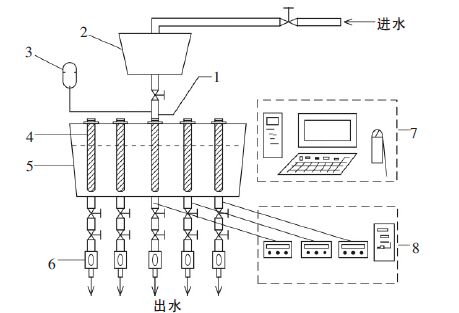1.长水口； 2.钢包； 3.示踪剂加入器； 4.塞棒；5.中间包； 6.流量计；7.RTD 系统； 8.数据采集系统 图 2 实验装置示意图

1.3 实验方案

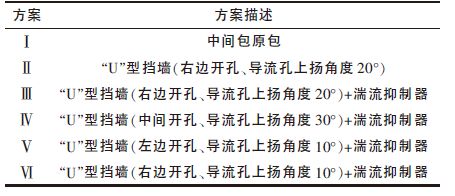
首先考察中间包原包内流体流动特性，然后在原包的基础上增设不同类型的“U”型多孔挡墙，在冲击区加设湍流抑制器，考察两者组合对中间包流动特性影响.挡墙分上下开孔，两孔孔径相等，孔间距z 为67 mm, 下孔距挡板下沿距离y 为102 mm, 开孔位置分为左边、中间、右边，距中心挡板距离xi分别为56 mm、127 mm、168 mm, 多孔挡墙示意图如图 3 所示.采用圆筒形湍流器抑制如图 4 所示.实验方案见表 2.

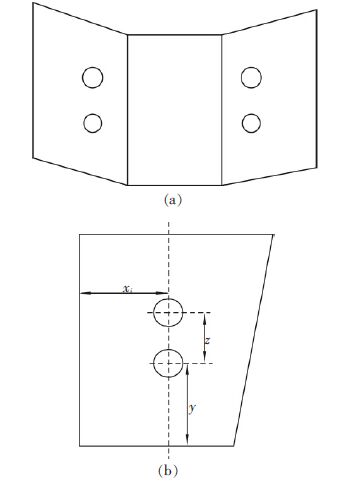图 3 多孔挡墙示意图

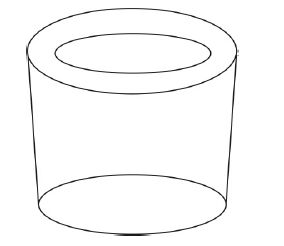图 4 湍流抑制器示意图

表2 实验方案
点击放大

2 实验结果与分析

方案Ⅰ～方案Ⅵ的RTD 曲线如图 5 所示.各方案的RTD 曲线数据分析结果如表 3、表 4 所示.

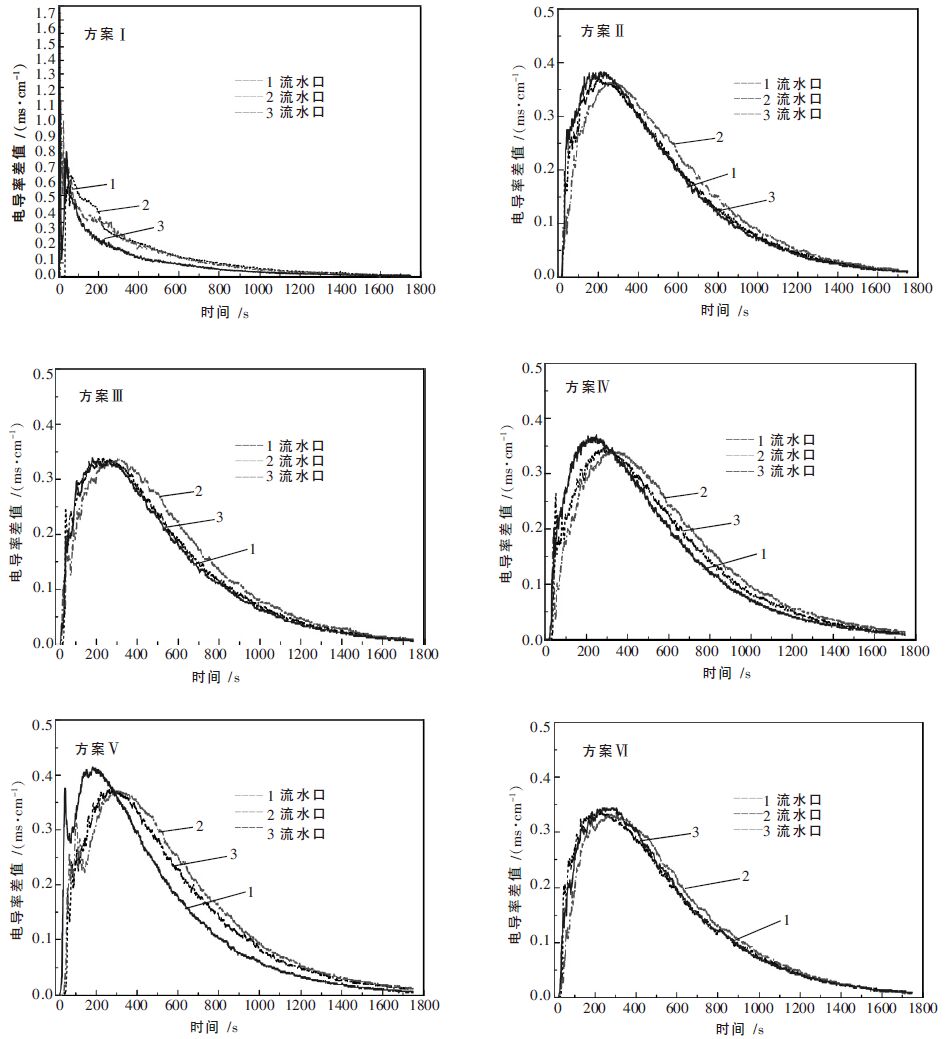图 5 方案I～方案VI 的RTD 曲线图

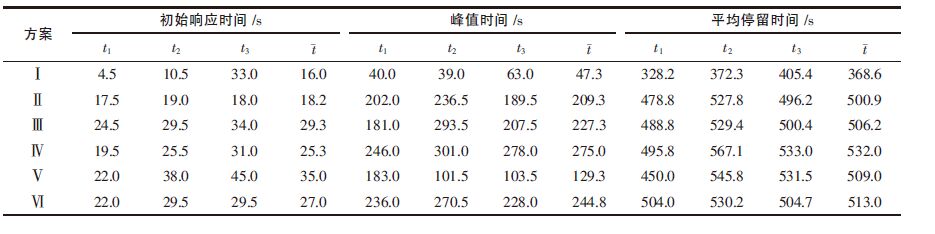
表3 中间包模型内模化介质的停留时间特征
点击放大

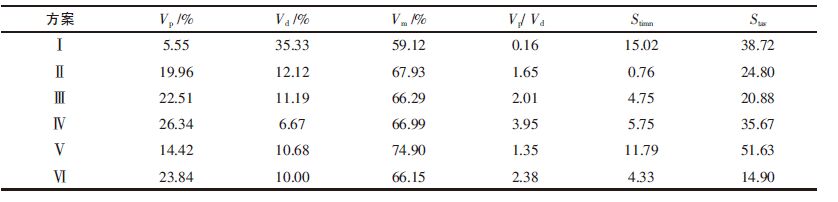
表4 中间包内的流动模式和流动均匀性
点击放大

方案Ⅰ为中间包原包，无任何控流装置.由图 5可以看出1 流、2 流曲线出现陡峰，说明有短路流存在.由表 3、表 4 可以看出，各流初始响应时间较短，1 流水口仅为4.5 s, 表明钢水由冲击区直接流向水口，钢水中夹杂物来不及有效上浮，便流进结晶器，降低铸坯质量.各流平均停留时间最大差值达77 s, 标准差为38.72，表明各流流动状态非常不一致.活塞区体积分数仅为5.55 %，而死区体积则高达35.33 %，说明钢液在中间包内混均效果不好.较大的死区体积以及各流间较大的流动特性差别，会造成包内的温度分布不均，同时也不利于夹杂物充分上浮，严重影响生产的顺行及对产品质量的有效控制.

方案Ⅱ～Ⅵ在方案Ⅰ的基础上增设多孔挡墙，通过变换导流孔的位置、开孔角度以及添加湍流抑制器来优化中间包流场.方案Ⅴ在挡墙左边开孔，结合表 3、表 4 和图 5 与方案Ⅰ对比可知，1 流、2 流曲线的陡峰明显减小，表明短路流现象得到明显改善.但各流平均停留时间差值为81 s, 平均停留时间标准差为51.63，表明各流之间流动特性差别增加.说明方案Ⅴ虽然可以有效地改善短路流，但中间包内流场分布反倒更不均匀.方案Ⅳ将开孔位置移到中间，完全消除了短路流现象，平均停留时间差值为37.5 s, 平均停留时间标准差为35.67，虽然较原包各流分布均匀性有一定改善，但效果仍然不是很理想.

方案Ⅱ、Ⅲ、Ⅵ将开孔设置在挡墙右边，由图 5 可以看出，3 个方案中各流的RTD 曲线分布比较一致，其中方案Ⅵ的各流RTD 曲线光滑，重合性最好.由表 3 可知，方案Ⅵ中1 流的响应时间由原包的4.5 s延长为22 s, 3 流的初始响应时间由原包的33 s 降到29.5 s, 由表 4 可知，初始响应时间标准差由原包的15.02 降为4.33，表明钢水由注流区经导流口到达1 流和3 流的时间差明显降低，流动趋于一致，有利于浇注操作.由表 3、表 4 可以看出，方案Ⅵ中各流平均停留时间的平均值由原包的368.6 s 增加到513 s, 钢水在包内平均停留时间增加，有利于钢中夹杂物上浮，净化钢液.各流平均停留时间标准差由原包的38.72 降为14.9，在所有方案中最小，表明各流流动趋于一致，钢水在包内混匀性最好.活塞区体积分数由5.55 %增加到23.84 %，死区体积由35.33 %降为10 %.活塞区体积分数与死区体积分数之比由原包的0.16增加到2.38.活塞区体积增加，死区体积的减少也进一步说明了钢水在包内流动性更好，使得包内的温度更均匀，且有利于夹杂物的去除.针对以上各方案，综合比较，方案Ⅵ是各种方案中最有利于中间包流场均匀分布的方案，是本次实验的最优方案.

3 结论

（1）原型中间包存在明显的短路流现象，存在较大死区，死区体积分数为35.33 %，不利于钢液中夹杂物充分上浮.各流开始响应时间和平均停留时间的离散度较大，流动一致性较差，钢液流动分布不均匀.

（2）在原型中间包的基础上，增设多孔挡墙和湍流抑制器，通过调整开孔位置及开孔角度优化中间包流场分布，方案Ⅵ有效地延长了平均停留时间，增加活塞区体积，降低死区体积，是各种方案中最有利于中间包流场均匀分布的方案，是本次实验的最优方案.

参考文献
[1] 蔡开科, 程士富. 连续铸钢原理与工艺[M]. 北京: 冶金工业出版社 , 2007.
[2] 左祥均. 重钢五流方坯连铸中间包内钢液流动和夹杂物运动的研究[D].重庆:重庆大学,2006.
[3] 段善勇.重钢五流方坯连铸中间包控流装置及冶金效果的研究[D]. 重庆:重庆大学,2003.
[4] 张体广.五流小方坯中间包的结构优化研究[D].沈阳:东北大学, 2008.
[5] 彭琦.八流中间包控流装置的优化研究[D].武汉:武汉科技大学, 2009.
[6] 陈伟庆. 冶金工程实验技术[M]. 北京: 冶金工业出版社 , 2004.
[7] ZHENG Shu-guo, ZHU Mao-yong. Optimization of baffles in a sixstrand round bloom cont inuous casting tundish: a physical modeling study[J]. Ironmaking and Steelmaking, 2006, 33(5): 398–401. DOI: 10.1179/174328106X113940.
[8] 陈远清, 文光华, 祝明妹, 等. 四流大方坯连铸中间包的物理模拟研究[J]. 钢铁钒钛, 2006, 27(2): 33–37.
[9] 李永祥, 程乃良, 陈志平, 等. 三流Τ 型中间包内控流装置优化的物理模拟[J]. 中国冶金, 2008, 18(2): 35–38.
[10] 韩丽辉, 王静松, 王永胜. 六流连铸中间包结构优化的水模型实验[J]. 钢铁钒钛, 2009, 30(2): 33–37.
[11] 李晓柄, 崔怀周, 陈伟庆, 等. 小方坯连铸六流中间包结构优化水模型研究[J]. 上海金属, 2010, 32(5): 46–50.
[12] 杨树峰, 石少清. 水平连铸中间包内钢水流动的水模型研究[J]. 特殊钢, 2009, 30(4): 22–25.
[13] 程志洪, 帅勇, 周俐. 五流小方坯中间包内型优化水模实验[J]. 安徽工业大学学报, 2009, 26(2): 118–120.
[14] 刘旭峰, 周俐, 王建军, 等. 六流小方坯连铸中间包内型优化设计水模研究[J]. 安徽工业大学学报, 2002, 13(1): 126–128.
[15] 王德永, 冯丽萍, 刘承军, 等. 几种中间包控流装置的作用及比较[J]. 钢铁研究学报, 2008, 20(8): 21–24.
[16] 王建军, 包燕平, 曲英. 中间包冶金学[M]. 北京: 冶金工业出版社 , 2001.
[17] 钟良才, 史迪, 陈伯瑜, 等. 七流方坯连铸中间包结构优化[J]. 东北大学学报:自然科学版, 2010, 31(7): 973–977.