| 基于贝叶斯网络的发动机曲柄连杆机构可靠性分析 |
曲柄连杆机构是发动机的重要组成部分,在发动机中起着动力传递的作用,它的工作状态直接影响发动机的输出性能,因此其可靠性关系到整个系统能否正常运行.由于曲柄连杆机构在工作中承受各种复杂的、周期性变化的拉力、压力及惯性力等外载荷,常常可能出现连杆断裂,活塞拉缸等失效现象.而现有的可靠性分析方法,如故障树和故障模式及影响分析等,主要局限于对系统的定性分析和简单定量评价,而在当给定部分部件的状态概率时,其对整个系统影响的条件概率的计算存在一定的困难[1].
由于贝叶斯网络是基于概率和统计理论,具有自然的表达方式、强大的推理能力和方便的决策机制等许多优点,运用其进行系统可靠性分析可以弥补传统可靠性分析方法的不足[2-3].目前,已有贝叶斯网络在可靠性方面的研究,如厉海涛等[4]将贝叶斯网络应用于动量轮可靠性建模与评估中;尹晓伟等[1]针对现有组合法与状态法在可靠性评估方法中的局限性,对基于贝叶斯网络的系统可靠性评估新方法进行了研究,并进一步利用贝叶斯网络对多状态系统可靠性进行定性分析和定量评估;钱文学等[5]利用贝叶斯网络研究了多态性机械系统可靠性的离散化建模方法;Torres 等[6]在可靠性框图和贝叶斯网络的映射方面作了相关工作; Bouissou 等[7]利用贝叶斯网络解释了如何在一个多状态系统上执行有效性的计算;周忠宝等[8]将贝叶斯网络用于系统的概率安全评估中; 贝叶斯网络在故障诊断策略优化中也有相应的应用[9].本文在以上研究的基础上,利用贝叶斯网络不确定性推理和图形化表达的优点提出一种基于贝叶斯网络的曲柄连杆机构可靠性分析方法,以评估其可靠性,识别系统中的薄弱环节.
1 贝叶斯网络概述一个有N 个节点的贝叶斯网络可以用B(G,P)来表示,G=(V,E) 是具有N 个节点的有向无环图,节点V 表示属性、状态等随机变量,而节点变量间的定性依赖关系可以用有向边E 来表示.P 为G 中节点所对应的条件概率分布,以定量的形式描述节点之间的概率依赖关系[10].
按照贝叶斯公式给出的概率公式定义:
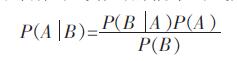
|
(1) |
式(1)中,P (B) 为先验概率,P (A|B) 为后验概率,P (B|A) 为似然率.
若A 是一个变量,且存在n 个状态a1,a2,…,an,则根据全概率公式可有式(2):
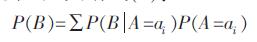
|
(2) |
通过以上的条件可以算出后验发生概率P(A|B).
贝叶斯网络具有变量间的独立性,能够实施双向推理.既可以由先验概率推导出后验概率,也可以由后验概率推导出先验概率,也就是说可以由因到果,也可以由果寻因.当节点变量给定时,可以计算网络正常的概率;当网络故障时,可以计算节点变量发生故障的概率,从而对系统的薄弱环节进行诊断.
贝叶斯网络提供了在给定父节点概率分布的情况下节点变量概率分布.以Pa(t)表示节点T 的父节点,则节点T 的概率分布为P(T),如式(3)所示:
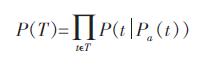
|
(3) |
发动机曲柄连杆机构重要的组成部件有活塞,连杆机构,气缸,曲柄,飞轮等.在工作的过程中,由于应力的复杂性常常造成气缸套磨损,曲轴断裂,烧瓦,拉缸,活塞故障等.本节分析活塞发生故障的原因并构造故障树,如图 1 所示. 图 1 中底事件从A1到A15分别为:机油窜入、相互摩擦、修配不当、气缸磨损严重、气体温度过高、燃烧室内积炭严重、气缸垫过薄、缸体顶面磨削过多、活塞与汽缸配合间隙过小、活塞环折断、活塞销卡环松脱或折断、高温高压、气体腐蚀和氧化、喷油提前角过大、汽缸壁润滑不良.
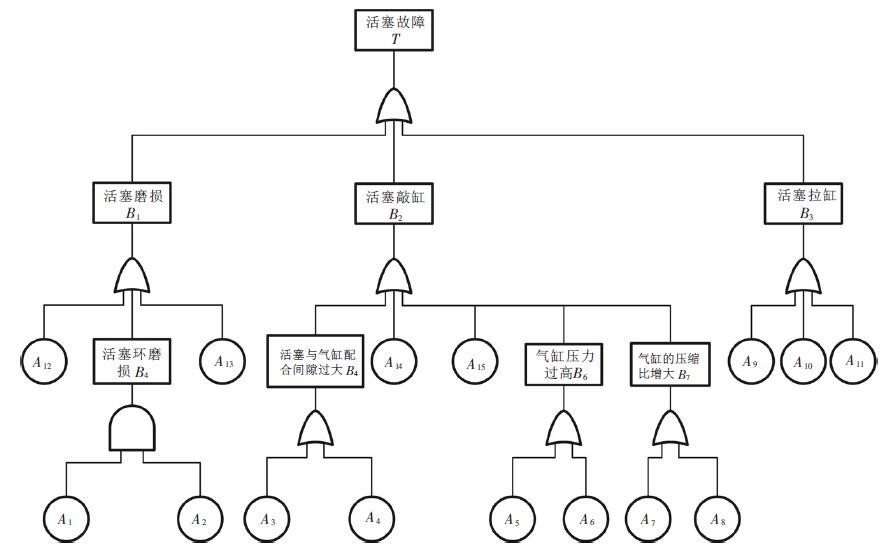 |
| 图 1 曲柄连杆机构“活塞故障”故障树 |
图 1 中各底事件间相互独立,且设底事件和系统只处于两种状态:工作(0)和失效(1).各底事件的故障概率如表 1 所示.
| 表1 各底事件的故障概率 |
 |
| 点击放大 |
应用故障树进行分析时,随着系统底事件数量的增加,系统的计算量呈指数倍的增长.从图 1 中可以看出,曲柄连杆机构活塞故障故障树底事件的数目较多,对于找出故障树的最小割集,或计算顶事件发生的概率,系统的重要度等计算量较大.因而可以直接的把系统的故障树转化成贝叶斯网络,解决故障树分析所出现的难题.
3 基于贝叶斯网络的可靠性分析方法贝叶斯网络的结构与故障树的结构是对应的,可以用贝叶斯网络的节点来表示故障树的逻辑门关系,也就是说,故障树中逻辑门间的关系可以用贝叶斯网络中的条件概率分布来反映.
故障树向贝叶斯网络转化算法如下[11]:
(1) 把故障树中每个底事件映射为贝叶斯网络中的一个节点;
(2) 把故障树中的每个逻辑门映射为贝叶斯网络中的一个节点;
(3) 连接输入事件对应节点与其所在逻辑门对应的节点;
(4) 在底事件失效分布已经确定的条件下,确定网络中根节点的先验概率分布;
(5) 依据故障树中逻辑关系确定贝叶斯网络中非根节点的条件概率分布.
依上述方法将图 1 所示的故障树映射为贝叶斯网络如图 2 所示. 其中B4为与门结点,T,B1,B2,B3,B5,B6,B7为或门结点.
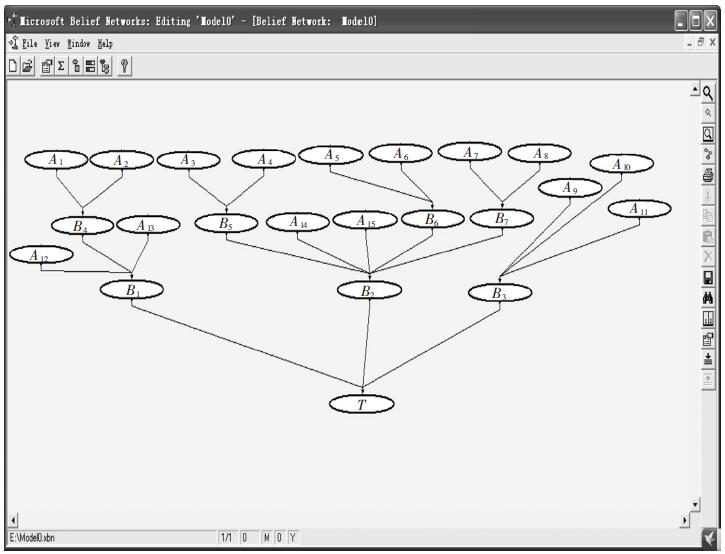 |
| 图 2 曲柄连杆机构活塞故障贝叶斯网络 |
当对模型进行故障诊断与推理时,假如系统处于故障状态,计算底事件的故障概率公式如式(4)所示:
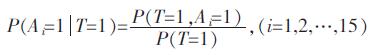
|
(4) |
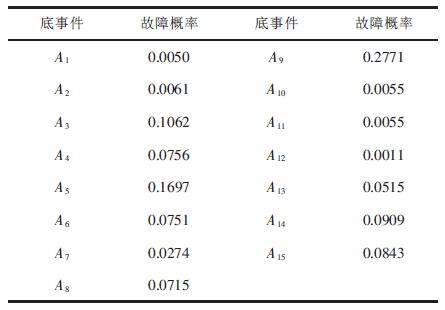
可以得到各底事件故障的条件概率,见表 2.
| 表2 系统故障状态下各底事件的故障发生概率 |
 |
| 点击放大 |
由表 2 可见,底事件A9的故障概率相对较大,认为其是系统中相对最为薄弱的环节.
对于系统的因果推理,若网络中各底事件为故障状态,则网络中节点的故障概率公式可以表达为式(5):
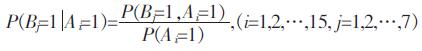
|
(5) |
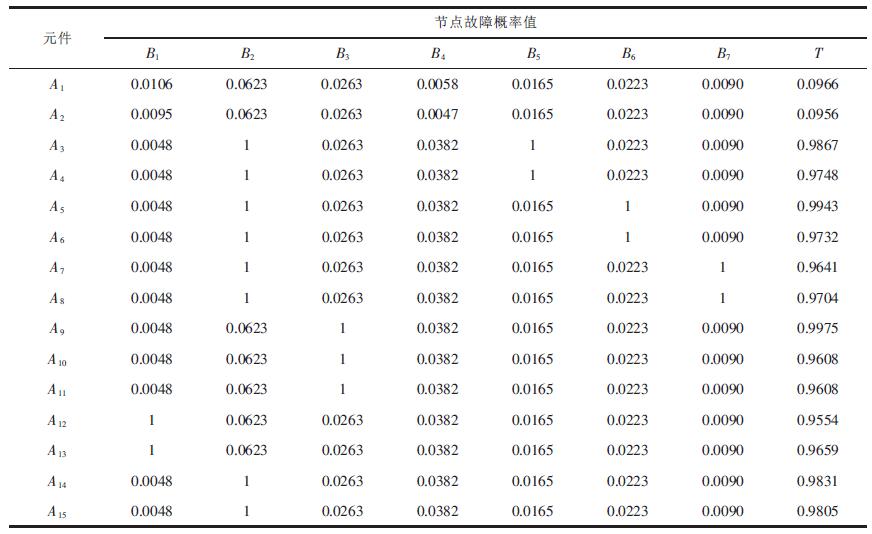
由此可以计算得到网络中节点的故障概率,见表 3.
| 表3 若底事件为故障状态时网络各节点故障概率 |
 |
| 点击放大 |
由表 3可见,各个底事件对于系统可靠性的影响是不同的,意味着在系统中所处的权重是不同的,因而依此可以确定系统的薄弱环节,为提高系统的安全性与可靠性,实施故障诊断与预测提供必要的参考.
4 基于贝叶斯网络的重要度分析可靠性分析中运用重要度概念来评估故障树中各底事件对于后果发生概率的影响.而运用贝叶斯网络能够方便地分析底事件对各个后果的影响程度.针对本例,计算RRW 重要度、FV 重要度、RAW 重要度和BM 重要度,其计算公式如式(6)~(9)所示:
(1) Risk Reduction Worth(RRW)重要度
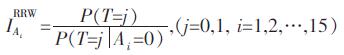
|
(6) |
(2) Fussel-Vesely(FV)重要度
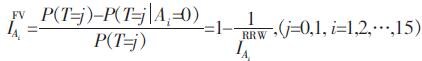
|
(7) |
(3) Risk Achievement Worth(RAW)重要度
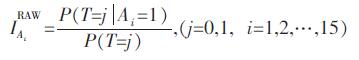
|
(8) |
(4) Birnbaum Measure(BM)重要度
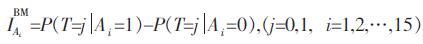
|
(9) |
依公式(6)~(9)可得每个底事件的重要度如图 3 所示.
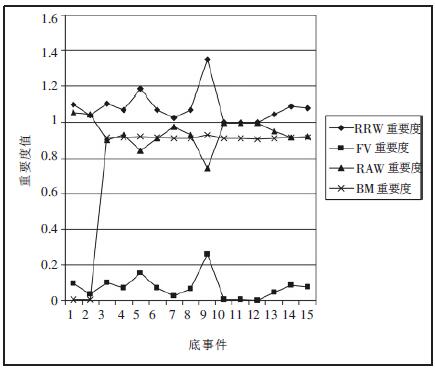 |
| 图 3 各元件的重要度值 |
从图 3 也可以看出,底事件9 对后果发生概率具有最大的影响,是系统中相对最为薄弱的环节,应加以重视.
5 结论(1) 利用贝叶斯网络对发动机的曲柄连杆结构进行可靠性分析不需要对其系统进行最小割集的求解,并且可以避免不交化的计算过程,减少了大量的计算,使对其分析更加方便,直观.
(2) 基于贝叶斯网络的可靠性分析方法能够很好的表示出其变量的相关性和随机不确定性特点,且通过对系统进行双向推理,能够实施系统中相对薄弱环节的准确定位,从而为提高系统的安全可靠性和故障诊断与预测提供有力的支持.
| [1] | 尹晓伟, 钱文学, 谢里阳. 系统可靠性的贝叶斯网络评估方法[J]. 航空学报, 2008, 29(6): 1482–1489. |
| [2] | 徐格宁, 李银德, 杨恒, 等. 基于贝叶斯网络的汽车起重机液压系统的可靠性评估[J]. 中国安全科学学报, 2011, 21(5): 90–96. |
| [3] |
Bobbio A, Portinale L, Minichino M, et al. Improving the analysis of dependable systems by mapping fault trees into Bayesian networks[J].
Reliability Engineering and System Safety, 2001, 71(3): 249–260. DOI: 10.1016/S0951-8320(00)00077-6. |
| [4] | 厉海涛, 金光, 周忠宝. 基于贝叶斯网络的动量轮可靠性建模与评估[J]. 系统工程与电子技术, 2009, 31(2): 484–488. |
| [5] | 钱文学, 尹晓伟, 谢里阳. 多状态机械系统可靠性的离散化建模方法[J]. 东北大学学报, 2008, 29(11): 1609–1612. |
| [6] |
Mahadevan S, Rebba R. Validation of reliability computational models using Bayes networks[J].
Reliability Engineering and System Safety, 2005, 87(2): 223–232. DOI: 10.1016/j.ress.2004.05.001. |
| [7] |
Bouissou M, Pourret O. A Bayesian belief network based method for performance evaluation and trouble shooting of multistate systems[J].
International Journal of Reliability Quality and Safety Engineering, 2003, 10(4): 407–416. DOI: 10.1142/S0218539303001275. |
| [8] | 周忠宝, 周经伦, 金光, 等. 基于贝叶斯网络的概率安全评估方法研究[J]. 系统工程学报, 2006, 21(6): 636–643. |
| [9] | 李俭川, 胡茑庆, 秦国军, 等. 控制与决策, 2003,18(5):568-572[J]. 控制与决策, 2003, 18(5): 568–572. |
| [10] | Pearl J. Probabilistic reasoning in intelligent systems: networks of plausible inference[M]. San Mateo: Morgan Kaufmann Pub , 1988. |
| [11] | 周忠宝. 基于贝叶斯网络的概率安全评估方法及应用研究[D]. 长沙: 国防科学技术大学, 2006. http://cn.bing.com/academic/profile?id=68603ca5b58eda72ed12f6bbd59a10fb&encoded=0&v=paper_preview&mkt=zh-cn |
 2012, Vol. 3
2012, Vol. 3

