| 3 -RPS 并联机器人位置分析及控制仿真 |
并联机构的位置分析在并联机器人的研究中具有十分重要的意义,通过位置分析可以求解机构的输入与输出构件之间的位置关系,是机构运动分析最基本的任务,以及是机构受力分析、速度、加速度、误差分析、机构综合分析等的基础[1].由于并联机器人机构具有刚度高,承载能力强,结构紧凑等优点,因此它在工业生活中具有广阔的应用前景.少自由度并联机器人机构运动学、动力学研究相对简单,具有很强的灵活性,制造相对容易,有其诸多优越性,在各个领域中更具有应用潜力,因而成为国内外学者研究较多的一类机构.在串联机器人的机构位置分析中,正解比较容易,反解比较困难,相反在并联机构位置分析中反解相对简单,而位置正解比较复杂.
目前,国内外对并联机器人机构位置正解主要有解析法和数值法.它们各有自己的优缺点:数值法数学模型相对简单,能够适用于大多数的并联机构,但它不能求出全部位置的解,国内外学者对此作了大量的研究.例如Innocentit 提出了位置正解的一维搜索法,Dagupta 提出了预测校正法,该方法采用3维搜索法从纯几何角度求解位置正解,有学者提出一种逐次逼近法;解析法,即利用各种数学消元法逐一消去未知数,最终求解一个一元多项式.虽能求出全部位置的解,但求解过程比较繁琐,国内对位置正解解析法的研究主要是北京邮电大学机械学研究所进行的,至今,他们分别获得了3-TPS、3-6SPS、5-4型、6-4 型机构、6-4 台体机构、6-5 型机构、5-5 型、6-5 型机构的位置正解,并验证了机构解的数目[2].
在控制领域中,控制方法很多,有PID 控制、滑模变结构控制、自适应控制法、模糊控制、神经元控制等,其中PID 控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好、可靠性高等特点,因而在控制领域中得到广泛的应用[3].
本文在借鉴前人的基础上,以3-RPS 并联机器人为例,应用坐标变换法和封闭方法对并联机器人机构位置作了初步的分析,并运用Matlab 建模与 PID 控制进行仿真.
1 机构描述3-RPS 并联机构的上下平台以3 个分支相联,每个分支由3 个运动副连接而成,固定平台的每个顶点各自连接一个转动副,转动副通过一个移动副连接一个球副,每个球副分别连接在移动平台的各个顶点,上下平台都是由2 个正三角形组成,如图 1所示.
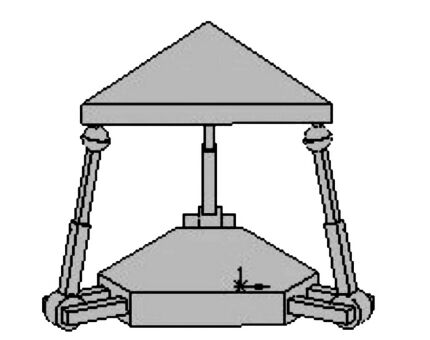 |
| 图 1 3-RPS 机构模型 |
在机构的上下平台上各建立坐标系,动坐标系 P-UVW 建立在上平台,下平台建立定坐标系OXYZ,P、O 分别在上下平台的中心.上下平台分别记为B1B2B3,A1A2A3,其中PBi,OAi,OBi分别记为bi,ai,qi,bi,ai的长度分别记为h、g,di表示驱动杆AiBi之间的杆长,Φi分别为连杆AiBi与下平台之间的倾斜角,θi分别表示转动副轴线ui与X 轴之间的夹角,L 为上平台三角形的边长,如图 2 所示.
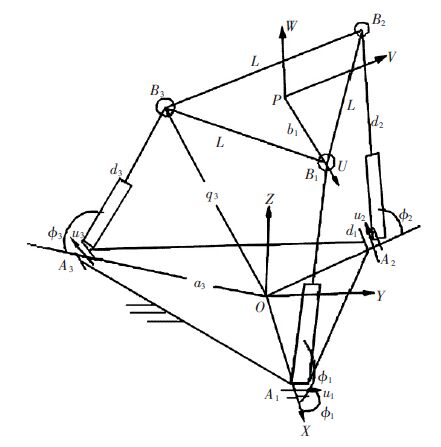 |
| 图 2 3-RPS 机构示意图 |
2 位置分析 2.1 位置反解
位置反解,即给定上平台在空间的位置和姿态,求各个杆长,即各移动副的位移[4].如图 2 可知,Ai在 O-XYZ 中的坐标为:
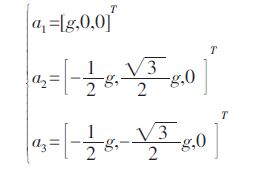
|
(1) |
Bi在P-UVW 中的坐标为:
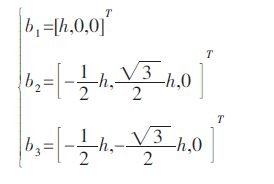
|
(2) |
取Z-Y-X 型欧拉角(α,β,γ),则动坐标系相对固定坐标系的方向余弦为:
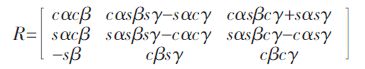
|
(3) |
式(3)中:cα=cosα,sα=sinα,其它同理.球铰在固定坐标系中的坐标为:
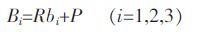
|
(4) |
式(4)中 P= [PX PY PZ ]T,表示动平台中心点在固定坐标系中的位置矢量.
由上可求出杆长:
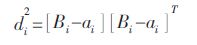
|
(5) |
从而求出该并联机器人的位置反解.
2.2 位置正解并联机构的位置正解即给定各分支的驱动长度 di,求动平台中心点P 在固定坐标系中位置坐标PX 、 PY 、PZ和动坐标系对定坐标系的方向余弦,即T.根据3-RPS 并联机构的结构特点,动平台由一个正三角形组成,由此可以运用梁崇高教授所提出的位置封闭解的方法来求解该并联机构的位置正解[5-6].
u1、u2、u3分别是3 个转动副的轴线方向,假设将球铰B1与动平台B1B2B3解除约束,由于与下平台连接的转动副的转动作用,显然杆B1A1会绕转动副的轴线u1转动,形成以A1为圆心,半径为d1的圆.同理,球铰B2、B3在相同的条件下也作相同的运动.假设u1、u2、u3与X 轴夹角分别为:θ1=90°、θ2=210°、θ3=330°,则上平台上的3 个球铰的位置分别用Φ1、Φ2、Φ3表示为:
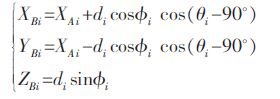
|
(6) |
动平台的三个顶点坐标表示上平台三角形的边长,边长为L,则有如下关系式:
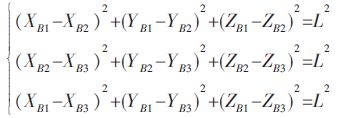
|
(7) |
将式(6)代入(7)中整理得到以Φi为参数的超越方程:
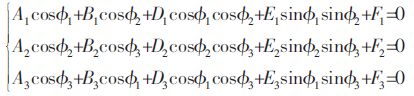
|
(8) |
式(8)中,Ai、Bi、Di、Ei、Fi均为已知量的函数.
令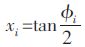
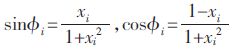
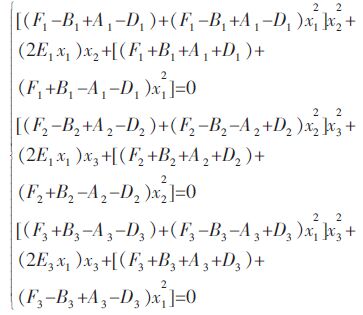
|
(9) |
化简得:
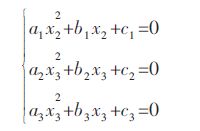
|
(10) |
式(10)中,ai、bi、ci为各阶变量x2和x3的系数.对上式进行化简消去x3,由于ai、bi、ci本身只含有x1、x2,则可以得到只关于x1、x2的方程:
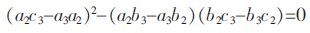
|
(11) |
将上式写成只关于x2的方程有:
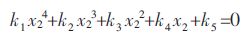
|
(12) |
式(12)中ki仅是关于x1的函数,再由式(10),式(12)可以写成如下矩阵方程:
| $$ | (13) |
由于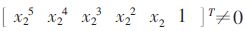
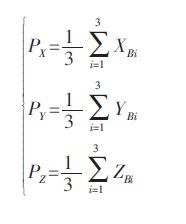
|
(14) |
假设动坐标系对固定坐标系的3 个转角分别为θU,θV,θW,则根据如下关系式求出方向余弦:
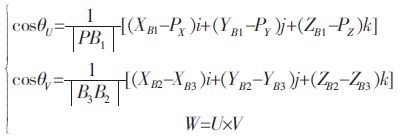
|
(15) |
式中:
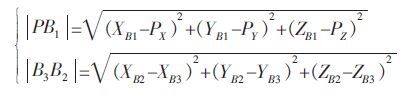
|
(16) |
根据控制原理与3-RPS 并联机器人的结构连接关系,运用Matlab 中SimMechanics 模块集,建立图 3、4、5、6 的仿真模型[7-10].
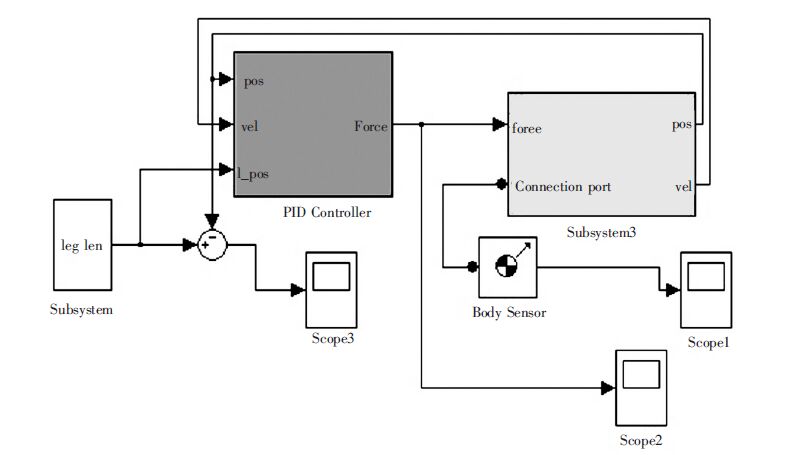 |
| 图 3 3-RPS 机构PID 控制SimMechanics 总框图 |
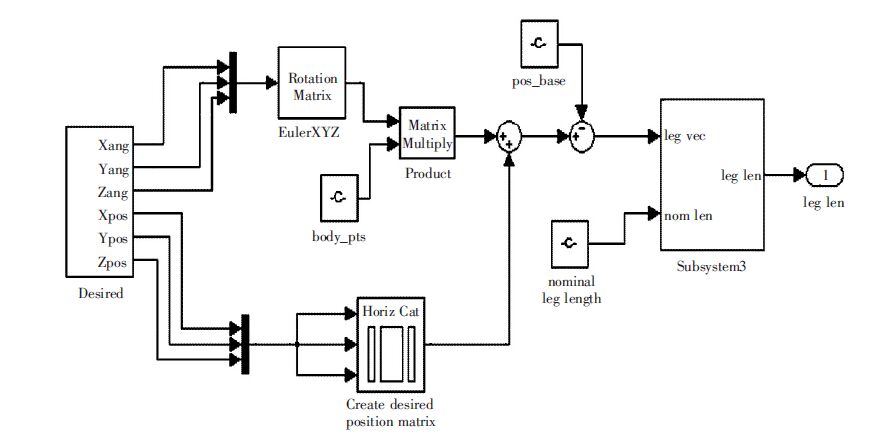 |
| 图 4 3-RPS 机构参考值输入SimMechanics 框图 |
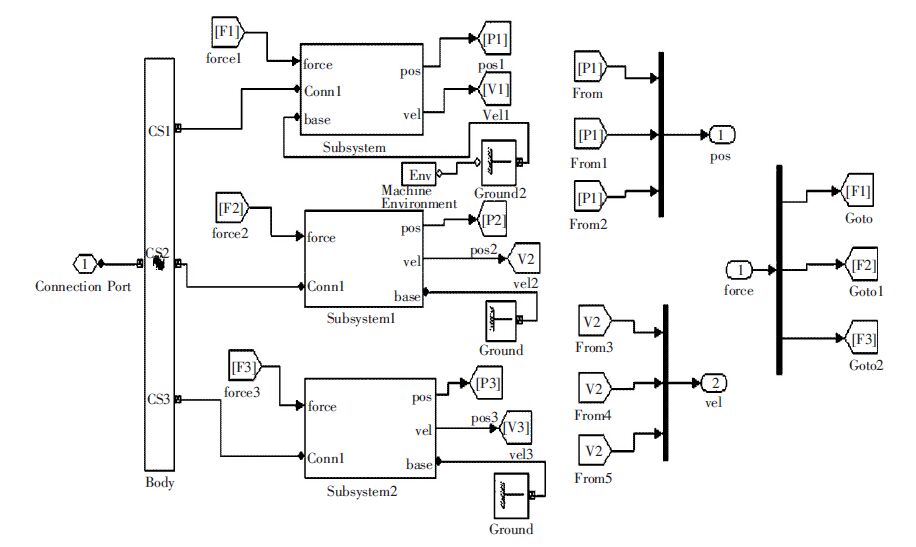 |
| 图 5 3-RPS 机构SimMechanis 框图 |
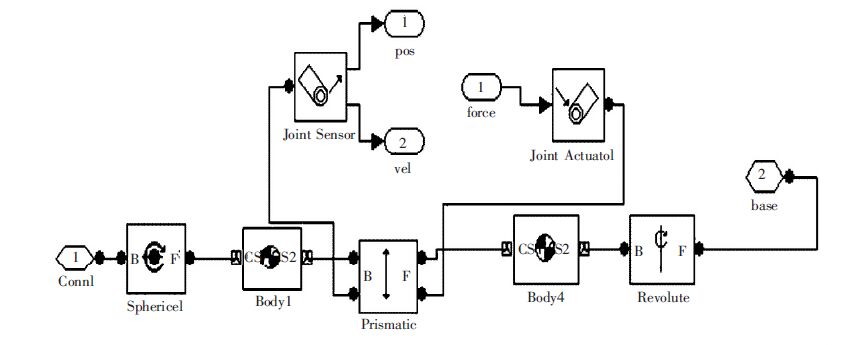 |
| 图 6 3-RPS 一支链SimMechanis 框图 |
图 3表示3 -RPS 机构建模仿真的总框图,Subsystem 部分表示对该机构系统输入的参考值,即图 4所示;PID Controller 部分表示控制部分;Subsystem3部分表示该机构,即图 5 所示;Scope1 与Scope3 为示波器,分别表示动平台的位置变化与差值的输出.
4 仿真对比分析设定初始参数: 上下平台外接圆半径分别为50 mm,100 mm,上平台的质量为1 kg,移动副固定杆和移动杆都为0.1 kg,上平台中心点P 的坐标为(0,0,150),Φ1=Φ2=Φ3=120°,建立机构模型.
假设动平台输入的参考值:EulerXYZ (45°,45°,0°),P 点的坐标输入为:(sin(2πt),sin(2πt),sin(2πt)),进行仿真,结果如图 7、图 8 所示.
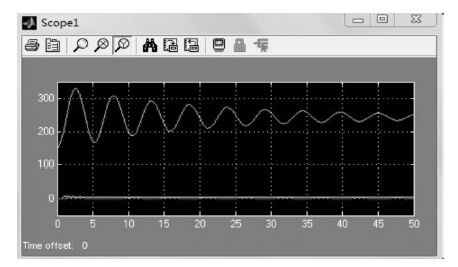 |
| 图 7 动平台位置变化图 |
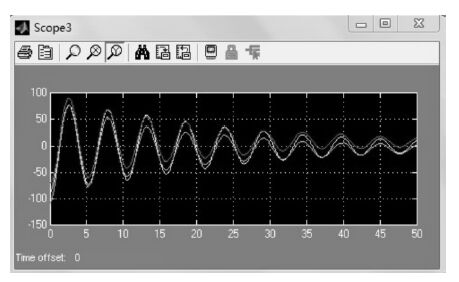 |
| 图 8 驱动杆实际输出与参考值的差值变化 |
改变P 点的参考坐标输入:(20sin (2π×5t+10)+10,20sin(2π×5t+10)+10,20sin(2π×5t+10)+10),进行仿真,结果如图 9,图 10.
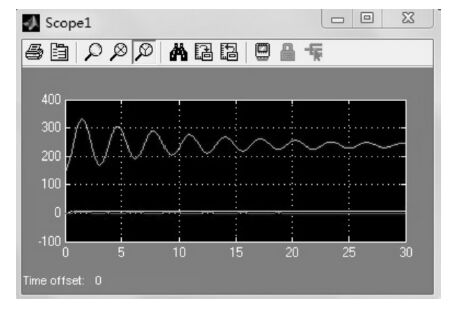 |
| 图 9 动平台位置变化图 |
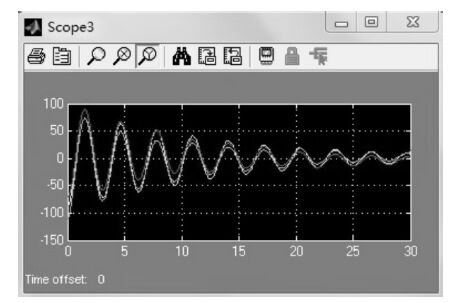 |
| 图 10 驱动杆实际输出与参考值的差值变化 |
比较图 7 和图 9 知,在不同的参考值输入的条件下,通过合理改变PID 控制器的参数,动平台中心点P 的X,Y,Z 轴的实际位置变化的变化规律几乎相同,体现了PID 的控制调平作用.由图 8 和图 10 可知,驱动杆实际输出值与参考值的偏差值逐渐趋于零,说明了PID 控制效果明显.
5 结论通过应用坐标变换法和位置封闭解法分析了3- RPS 并联机器人的正反解位置分析,为进一步分析该机构运动学与控制仿真提供了有效的理论基础.根据控制原理,运用Matlab 中SimMechanics 模块,建立机构模型与控制仿真模型,在不同状态下进行仿真比较,得出正确的图形;由结果分析可知,基于PID控制可实现并联机器人动平台的自动调平,在实践中具有重要的应用价值.驱动杆实际输出与参考值的误差值曲线在零附近上下波动,逐渐趋于零,但还是存在一定的偏差,这为进一步研究并联机器人控制性能的提高奠定了基础.
| [1] | 黄真, 孔令富, 方跃法. 并联机器人机构学理论及控制[M]. 北京 : 机械工业出版社 , 1997. |
| [2] | 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京 : 高等教育出版社 , 2006. |
| [3] | 朱大昌. 基于并联支撑机构的车载雷达天线自动调平系统研究[D]. 北京:北京交通大学,2008. |
| [4] | 付廷贵, 许瑛, 杨光. 3 自由度并联机构的位姿分析[J]. 南昌航空工业学院学报, 2005, 19(3): 25–31. |
| [5] | 李树军, 王阴, 王晓光. 3-RPS 并联机器人机构位置正解的杆长逼近法[J]. 东北大学学报, 2001, 22(3): 285–287. |
| [6] | 吴巍. 一种两自由度并联机构位置分析与仿真[J]. 机械设计与制造, 2011(5): 113–115. |
| [7] | 汪汇. 3-RRRT 并联机器人运动仿真的 SimMechanics 实现[J]. 现代机械, 2008(3): 44–48. |
| [8] | 刘胜, 李晚龙, 杜延春, 等. 并联机器人动力学与控制仿真研究[J]. 弹箭与制导学报, 2005, 25(7): 928–930. |
| [9] | 王永超. 基于 Matlab 的机构运动仿真方法及其比较[J]. 计算机仿真, 2004, 21(8): 81–83. |
| [10] | 梁毓明, 陈德海. 轮式移动机器人调速系统的设计[J]. 江西理工大学学报, 2008, 29(4): 13–16. |
 2012, Vol. 3
2012, Vol. 3

