| 渗透系数对饱和土强夯效果影响的数值模拟 |
实践证明,土的渗透系数对强夯过程和强夯效果有重要影响,但并未从理论上得到证明.由于强夯是一个复杂的动力过程,对强夯的解析分析难于进行,因此,数值分析成为研究强夯的重要方法.孟庆山[1] 编制了近场瞬变波动有限元程序DCDFEM 对强夯法加固饱和软粘土地基进行了流固耦合分析,得出强夯过程中土体动态响应的一般规律;周世良[2]考虑饱和地基土流固耦合、土体非线性和强夯处理大变形等特征,得到了夯坑变形、流场分布及孔隙水压力分布情况等结果;包旭范[3]分析了饱和土在受夯击时的变形及渗流情况,得出改变强夯排水条件可以有效加固饱和土地基;叶为民等[4]对强夯法加固饱和软土地基的效果进行了研究,也得出饱和软粘性土采用强夯法关键在于排水的结论.但上述研究分析侧重于对动力响应和加固机理的探讨,对加固效果、尤其是不同渗透系数对动力响应和加固效果的影响分析较少.
采用FLAC3D 数值计算软件,建立三维强夯计算模型,基于流固耦合、大变形和几何非线性理论,研究不同渗透性能的饱和土地基在单点单击作用下的强夯动力响应,分析不同渗透性能饱和土的加固效果,为强夯设计、施工控制以及对适宜强夯加固的饱和土的分类提供参考.
1 FLAC3D 数值方程和参数FLAC3D 采用求解动力方程的方法解决准静力问题和动力问题,采用显示差分法求解微分方程,在求解非线性问题时有较好的适用性;采用小变形的本构关系将各时步的变形叠加来求解大变形问题.流体和固体介质的耦合作用以准静态比奥固结理论和可渗透介质的单相达西定律为理论基础,式(1)~式(6)为FLAC3D 动力流固耦合实现的几个基本方程[5-6].
(1)流体传导方程
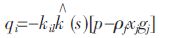
|
(1) |
式(1)中,qi为比流量矢量;p 为孔隙水压力;kil为流体渗透系数张量;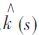
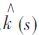
(2)流体质量平衡方程
土体中单位时间内流体体积的增加量应等于由于流体源的存在流进单元中的流体体积减去由于流体运动而流出单元的流体体积,即:
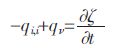
|
(2) |
式(2)中,qi,i为流体运动流出单元的流体体积;qν为流体源强度,/s-1;ζ 为每单位体积可渗透介质流体体积的变化;t 为时间,/s.
(3)流体连续性方程
描述孔隙水压力与饱和度、孔隙水体积、土体体应变和饱和度等变量之间的相互关系的流体本构方程为:
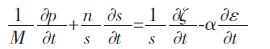
|
(3) |
由式(2)和式(3)可得流体的连续性方程:
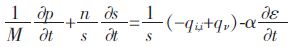
|
(4) |
式(4)中,M 比奥模量,/(N·m-2);α 为比奥系数;ε 为介质体积应变;n 为孔隙率.
(4)固体介质动量平衡方程
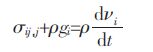
|
(5) |
式(5)中,ρs和ρw分别为固相和液相的密度;ρ=(1- n)ρs+nρw单位体积介质的质量;gi单位质量的体积力张量;νi为速度张量.
(5)几何相容方程
表述位移与应变之间的关系,将几何方程两边对时间求导即可得到采用速度变化率表达的应变率即:
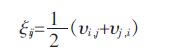
|
(6) |
式(6)中,ξij为应变率张量.
(6)渗透介质本构关系
双屈服模型是在应变硬化-软化模型的剪切和张拉破坏包络线的基础上增加了一个体积屈服面.剪切屈服势函数gs 对应于非相关联流动法则,张拉势函数gt 和体积势函数gν 对应于相关联的流动法则.
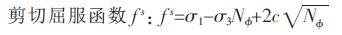
|
(7) |
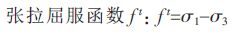
|
(8) |
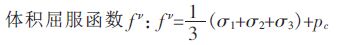
|
(9) |
式(7)~式(9)中:NΦ=(1+sinΦ)/(1-sinΦ),Φ为摩擦角; c 为粘聚力;σt 为抗拉强度;pc为帽盖压力; 主应力σ1、σ2和σ3(压应力为负),σ1≤σ2≤σ3.
将式(1)、式(6)代入式(4)与式(5)构成方程组通过空间离散和有限差分,可在给定的初始条件、边界条件和本构关系下求解应力、应变、孔隙水压力等相关变量.
2 强夯模型的建立 2.1 基本假定(1)土体为均质各向同性弹塑性体,不考虑温度的影响;
(2)不研究夯锤与地面的冲击过程,将强夯自由落体冲击地面动应力简化为一随动力时间变化的三角形拟静力荷载,且只分析单点单击效果;
(3)计算过程中考虑基于渗透系数改变的强夯效果,土体的其他初始物理力学参数与之相匹配;
(4)自由地下水位位于地表,流体流动符合达西定律且各方向渗透系数相同;
(5)土体颗粒和流体不可压缩(即比奥系数取1).
2.2 本构模型(1)土体本构模型.静力计算阶段采用弹性本构模型,动力流固耦合计算阶段采用FLAC3D 提供的适用于模拟产生不可恢复压缩变形和剪切屈服的岩土材料双屈服塑性模型,反应强夯动力荷载作用下地基土体的压密和塑性体积应变特性.
(2)流体本构模型.流体本构模型采用各向渗透系数相同的各向同性流体模型.
2.3 计算参数(1)土体与流体属性.力学计算涉及的物理力学参数主要包括弹性模量E、泊松比μ、粘聚力c、内摩擦角Φ、体积模量K、剪切模量G、土体干密度ρ;渗流计算中涉及的流体参数包括渗透系数k、流体密度ρw、流体体积模量Kw、饱和度s 和空隙比e.各参数[7]取值列于表 1 所示.
| 表1 材料物理力学参数 |
 |
| 点击放大 |
(2)动力载荷.采用文献[2]提供的三角形拟静力荷载形式:动应力升压时间为0.0306 s,降压时间为0.0612 s,最大接触动应力为2 MPa.夯锤底面半径取1.25 m,运用history 命令将拟静力设置为随动力计算时间变化的应力历史函数,将动应力竖直向下加载在地表夯锤区域.
2.4 模型网格划分为了准确反应工程真实情况、减少计算机负担和计算时间,数值模拟一般选择某一区域作为研究对象来分析;FLAC3D 数值计算结果是否精确与网格的划分密切相关,网格单元划分越细计算越精确,但所消耗的时间也越长.动力计算中网格单元尺寸[8]的要求与振动波在土体介质中传播的波长有关,应该满足式:
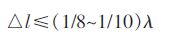
|
(10) |
式(10)中: △l 网格单元尺寸;/m,λ 振动波波长;/m.振动波又分为压缩波和剪切波,压缩波P 波在介质中的传播速度 
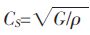
在求解动力波动问题,时间步距△t 的合理选取亦是非常重要,必须要保证计算的精度和稳定性.刘晶波[9]针对二维矩形单元证明了对集中质量有限单元而言,时间步距应该满足△t<△l/C.强夯引起的振动频率f 约为(6~20 Hz)[10-11],文中取20 Hz.由表 1 材料参数可求得振动波的传播速度,并且由式C=λ·f可求得波长λ 值,将其代入式(10)即可得到网格的最大单元尺寸,相关计算结果列于表 2 所示.
| 表2 动力计算相关参数表 |
 |
| 点击放大 |
文中计算区域选择采用20 m×20 m×10 m 空间范围.其中,地基土层厚度取10 m,夯点位于地表区域中心点位置.由单点单击强夯的特点,采用轴对称网格单元,建立尺寸为20 m×10 m×10 m 的计算模型.其中,模型x 方向为20 m、y 方向和z 方向为10 m.网格划分如图 1 和图 2 所示,对夯锤作用附近区域进行了网格加密,采用radcylinder 单元网格,整个模型共有15267 个节点和14080 个单元.
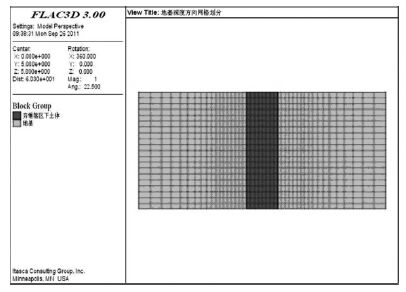 |
| 图 1 强夯地基深度(z)方向网格划分 |
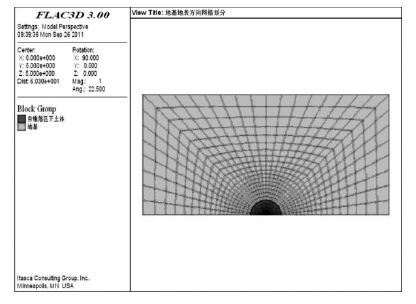 |
| 图 2 强夯地基地表(x,y)方向网格划分 |
2.5 边界条件及阻尼
(1)静力边界:利用fix 命令约束底部边界全部(x、y、z)向位移,约束4 个侧面边界横向(x、y 向)位移,顶部边界设置为自由边界;
(2)动力边界:利用apply nquiet squiet dquiet 命令把模型侧面边界和底部边界条件均设置为静态边界以减小动应力波在边界上的反射影响;
(3)流体边界:利用fix pp 0 命令将模型顶部边界条件设置为可透水边界,其余各边界均设置成不透水边界;
(4)阻尼设置:为减弱系统的自然振动模式的振幅,采用最易接受的瑞丽阻尼形式,最小临界阻尼比取5 %,最小中心频率采用模型的自振频率2.37 Hz,利用命令set dyn damp rayleigh 0.05 2.37 设置瑞丽阻尼[12].
3 求解及结果分析计算求解过程主要包括静力分析阶段和动力流固耦合分析阶段.静力分析是在小变形模式下通过设置弹性材料参数、流体模型参数、初始孔压场和静力边界条件,关闭流体和动力计算模式并将流体模量设置为0,在重力作用下达到平衡,获得动载施加前的初始应力状态; 动力流固耦合计算过程在大变形模式下打开流体和动力计算模式,施加动力边界条件和动载荷并且将流体体积模量设置为真实值,同时设置动态多步分析来有效减少计算时间.在计算过程中通过定义fish 函数和设置history 函数来监控相关节点变量值随计算过程的变化.
3.1 位移分析强夯地面变形是强夯设计中较为关心的参数之一,同时也是强夯加固效果的直接外在表现,也可以作为评价加固效果的间接指标.在完成静力和动力计算过程后可得到模型内任一节点的位移.夯锤中心下0 m(节点编号421)、1 m(节点编号400)、2 m(节点编号379)和地表距夯锤中心2 m(节点编号3584)处土体竖向位移时程曲线如图 3 所示(正值表示位移方向向上,负值表示位移方向竖直向下).通过图 3 可以看出从0 s 至0.0612 s 夯锤作用的瞬间,地基土发生了约为10 cm 沉降量,随着深度的增加沉降量逐渐减小;由于振动波传播过程的影响,最大沉降量时间相对于夯击结束时间出现滞后,夯锤下3 m 单击沉降量约为1.5 cm;从0.0612 s 至夯后0.1 s 土体由于自身的弹性特性出现位移回弹; 距夯锤中心2 m(节点编号3584)处地表土体竖向位移出现了正的位移,说明由于震动波的反射或者地基土的压密挤压作用使地表夯坑周围出现了隆起[13],但隆起量相对于夯坑沉降量较小.
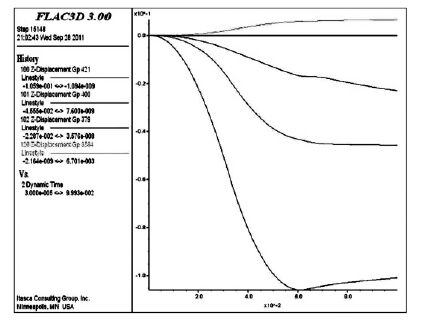 |
| 图 3 夯锤中心下0 m、1 m 和2 m 及距夯锤中心2 m 处地表节点竖向位移时程曲线 |
3.2 孔隙水压力分析
对于孔隙中充满水的饱和土在强夯动应力作用下会产生动孔隙水压力,它的消散会引起土体产生力学变形.从图 4 夯锤中心下1 m、2 m 和3 m 处土体节点孔压及接触应力时程曲线中可以看出,土层中动孔隙水压力峰值滞后于土层表面的接触动应力峰值;在冲击载荷升压阶段,由于土层内孔隙水压力的消散作用,土层内产生的孔隙水压力相对于相应节点处冲击荷载所引起的附加应力小;在卸荷阶段,当动应力峰值经过一定时间后,孔隙水压力则大于相应点处的附加应力,产生一定的残余孔隙水压力;由于动应力使接近地表的土层内产生大量裂缝,形成良好的排水通道促进孔隙水的排出,随着深度增加残余孔隙水压力也更大.
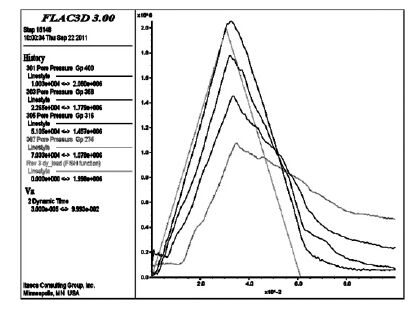 |
| 图 4 夯锤中心下1 m、2 m 和3 m 处土体节点孔压时程曲线 |
3.3 塑性体积应变分析
强夯加固的直接效果就是产生不可恢复的塑性体积压缩应变,从而增加地基土的密实度、提高变形模量和地基承载力、消除液化和湿陷性.夯锤中心下土体单元体积应变增量时间曲线如图 5 所示,在夯击瞬间单元体产生负的体积应变增量,即单元体积被压缩.该单元体密度的变化情况如图 6 所示,可知在夯击结束后单元体密度增大,单击前后密度从初始1680 kg/m3 升高到1758 kg/m3,密度变化的具体数值还与单元体网格大小有关.
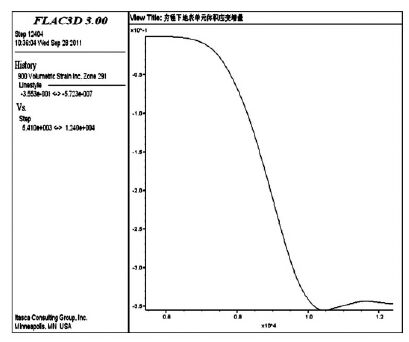 |
| 图 5 夯锤中心下0 m 处单元体积应变增量时程曲线 |
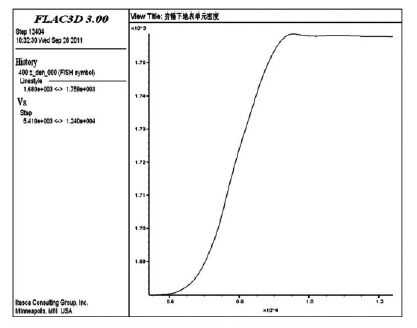 |
| 图 6 夯锤中心下0 m 处单元密度变化时程曲线 |
4 渗透系数影响分析
由于流体和固体的耦合作用,渗透系数的大小会间接影响土体的沉降、塑性体积应变和密度的变化.不同渗透性能饱和土体地基在强夯动应力作用下产生的动孔隙水压力将会不同,动孔隙水压力的消散情况也将会不一样.利用上文所建立的计算模型基于表 1所提供的材料参数,增加基于渗透系数为0.1 cm/s、0.01 cm/s 和0.0001 cm/s 的模拟结果.
4.1 位移对比经过4 次数值模拟计算,采用定义的fish 函数将计算结果导出.图 7 为4 种渗透系数情况下夯锤中心下地表土体竖向位移时程曲线图.从图 7 中可以看出,地表单击竖向位移或夯坑深度随渗透系数增大而增加;同时,渗透系数数量级越小,它对计算位移的影响也更小,可说明渗透系数对渗透性较小的粘性土或粉质土在强夯冲击瞬间加固的影响较小,可以通过增大土的渗透性能来增加夯击瞬间加固深度.
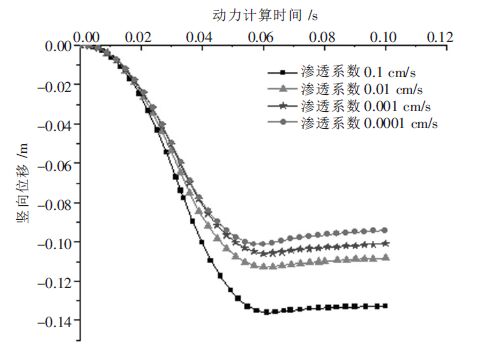 |
| 图 7 夯锤中心下地表土体竖向位移时程曲线 |
4.2 孔压对比
夯锤中心下1 m 处单元体不同渗透系数情况下孔隙水压力时程曲线结果如图 8 所示,从图 8 中可以看出渗透系数越大动孔压峰值越小,夯击结束后残余孔压也更少,说明渗透系数越大动孔压消散更快;对于相对较小的渗透系数0.001 cm/s 和0.0001 cm/s,动孔隙水压力的变化比较接近,可以说明渗透系数小到一定程度以后对强夯瞬间的动力响应影响较小.图 9 为夯锤中心下2 m 处单元体不同渗透系数情况下的孔隙水压力时程曲线,从图 9 中可看出渗透系数大的饱和土相对于渗透系数较小的饱和土孔压消散更快.
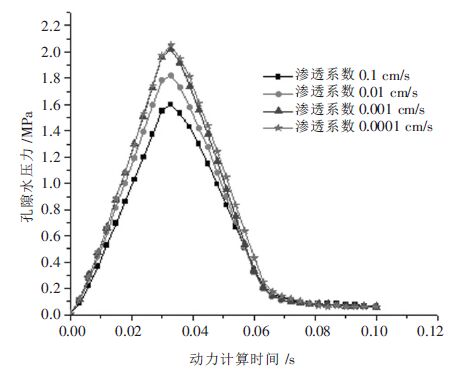 |
| 图 8 夯锤中心下1 m 节点孔隙水压力时程曲线 |
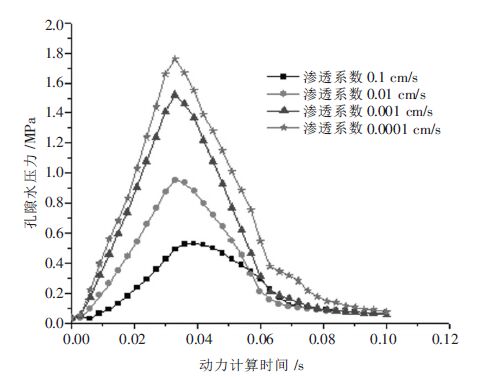 |
| 图 9 夯锤中心下2 m 节点孔隙水压力时程曲线 |
4.3 体积应变与单元密度对比
渗透系数分别为0.01 cm/s、0.001 cm/s 和0.0001 cm/s时的夯锤下地表单元体体积应变增量时程图如图 10所示,从图 10 中可知渗透系数为0.01 cm/s 相对于0.001 cm/s 和0.0001 cm/s 所对应的体积应变增量变化最大,渗透系数0.001 cm/s 和0.0001 cm/s 对应的体积应变增量更为接近.夯锤下地表单元体密度变化时间曲线图如图 11 所示,渗透系数为0.01 cm/s 所对应的密度增大到了2009 kg/m3,渗透系数为0.001 cm/s所对应的密度增大到1758 kg/m3,渗透系数较小的0.0001 cm/s 所增加的密度较小.
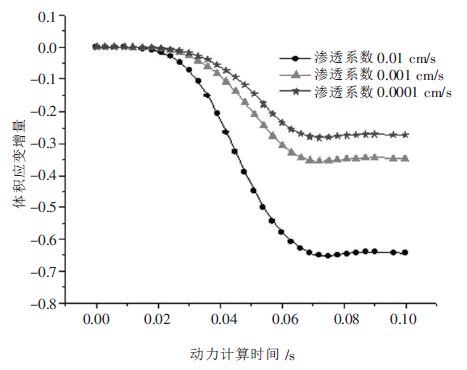 |
| 图 10 夯锤中心下地表单元体积应变增量时程曲线 |
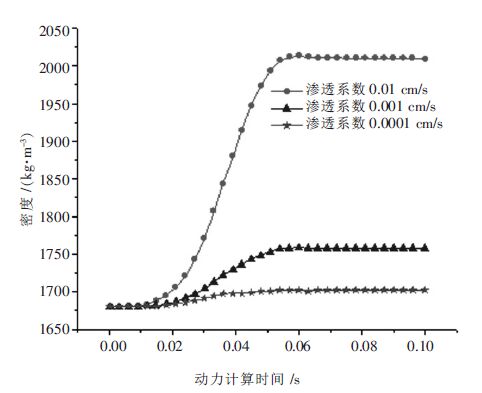 |
| 图 11 夯锤中心下地表单元密度时程曲线 |
5 结束语
利用FLAC3D 数值分析软件建立考虑非线性、大变形的饱和土三维强夯计算模型,对强夯过程进行了模拟并考虑了渗透系数对加固效果的影响,可得出如下结论:
(1)所建立的模型能较好地对饱和土强夯进行模拟,得出强夯时不同位置的位移、孔隙水压力、塑性体积应变和夯后土土体密度的变化情况.
(2)一定范围内的渗透系数对强夯瞬间的加固效果有一定影响,渗透系数越大加固效果越好;渗透系数小至一定值时,强夯效果不佳并对渗透系数的变化不明显; 在施工过程中可以尝试在一定范围内提高土的渗透性能或改进排水条件来提高强夯对饱和土类的加固效果.
| [1] | 孟庆山, 雷学文. 饱和软粘土强夯的流 、固耦合分析[J]. 武汉科技大学学报:自然科学版, 2003, 23(4): 364–366. |
| [2] | 周世良, 庞博, 郑红娟. 强夯加固饱和地基土的数值模拟[J]. 水运工程, 2009(4): 140–146. |
| [3] | 包旭范, 高强, 周顺华, 等. 强夯加固软土地基机理的有限元分析[J]. 中国铁道科学, 2005, 26(2): 8–14. |
| [4] | 叶为民, 唐益群, 杨林德, 等. 强夯法加固饱和软土地基效果研究[J]. 岩土力学, 1998, 19(3): 72–76. |
| [5] | 刘波, 韩彦辉. FLAC 原理 、实例与应用指南[M]. 北京 : 人民交通出版社 , 2005. |
| [6] | 刘洋, 周健, 付建新. 饱和砂土流固耦合细观数值模型及其在液化分析中的应用[J]. 水利学报, 2009, 40(2): 253–256. |
| [7] | 郑红娟.高填方饱和地基土强夯处理数值模拟研究[D].重庆:重庆交通大学,2008. |
| [8] |
LYSMER J, WAAS G. Shear waves in plane infinite structures[J].
Journal of the Engineering Mechanics Div, 1972, 98(EM1): 85-–105. |
| [9] | 刘晶波, 廖振鹏. 离散网络中的弹性波动(I11):时域离散化对波传播规律的影响[J]. 中国科学:B 辑, 1992(8): 574–582. |
| [10] | 褚宏宪, 史慧杰. 强夯振动监测应用分析[J]. 物探与化探, 2005, 29(l): 88–92. |
| [11] | 蒋维强, 欧阳立胜. 强夯地震效应特征研究[J]. 防灾减灾工程学报, 2005, 25(l): 45–48. |
| [12] | 陈育民, 徐鼎平. FLAC/FLAC3D 水电出版社,2009.基础与工程实例[M]. 北京 : 中国水利水电出版社 , 2009. |
| [13] | 王桂尧, 胡振南, 匡希龙. 红砂岩路基强夯处理大变形数值模拟方法与效果分析[J]. 岩土力学, 2008, 29(9): 2451–2456. |
 2012, Vol. 3
2012, Vol. 3

