有色金属科学与工程  2012, Vol. 3 Issue (1): 32-36
文章快速检索     高级检索
引用本文
0
车晓梅, 陈伟庆, 赵江, 马富平. 水口类型对大方坯连铸结晶器内流场和温度场的影响[J]. 有色金属科学与工程, 2012, 3(1): 32-36. DOI:10.13264/j.cnki.ysjskx.2012.01.018.
CHE Xiao-mei, CHEN Wei-qing, ZHAO Jiang, MA Fu-ping. Effects of SENs types on flow patterns and temperature distribution in bloom mold[J]. Nonferrous Metals Science and Engineering, 2012, 3(1): 32-36.DOI: 10.13264/j.cnki.ysjskx.2012.01.018.
水口类型对大方坯连铸结晶器内流场和温度场的影响[PDF全文]
车晓梅1, 陈伟庆1, 赵江2,3, 马富平2,3    
1. 北京科技大学冶金与生态工程学院，北京 100083;
2. 邢台钢铁有限责任公司，河北邢台 054027;
1. 河北省线材工程技术研究中心，河北邢台 054027
作者简介： 车晓梅（1985- ），女，硕士研究生 ，主要从事冶金过程数值模拟方向研究 ， E-mail：chexiaomei1121@163.com
收稿日期：2011-11-28
摘要：利用 Fluent 流体力学软件对直通式、侧二孔式、侧四孔式浸入水口对大方坯连铸结晶器内钢水流场和温度场进行了数值模拟.结果表明，从流场来看，直通式冲击深度最大，侧二孔式次之，侧四孔式最小，侧四孔式水口在结晶器内钢水能形成上、下两个回流，其下回流涡心较直通式水口从 590 mm 上移至 270 mm，有利于夹杂物的上浮.从温度场来看，侧二孔式和侧四孔式较直通式水口使结晶器内热中心明显上移，且其弯月面钢水温度比直通式分别提高了 6 K 和 4 K，有利于保护渣的熔化.
关键词： 水口    结晶器    流场    温度场    数值模拟    
Effects of SENs types on flow patterns and temperature distribution in bloom mold
CHE Xiao-mei1, CHEN Wei-qing1, ZHAO Jiang2,3, MA Fu-ping2,3    
1. School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Xingtai Iron and Steel Company, Xingtai 054027, China;
1. Hebei Wire Engineering Research Centre, Xingtai 054027, China
Abstract: The flow field and temperature distribution of molten steel in the bloom casting mold have been simulated under the conditions of single straight SEN, side two -furcated SEN, and side quad -furcated SEN by using hydrodynamic software fluent. Results showed that，seeing from flow field,the impingement depth of single straight SEN was the largest, that of side two-furcated SEN was larger, and the depth of side quad-furcated SEN was smallest. The upper and lower double rolls were formed in the side quad-furcated SEN mold. The vorticity of center of the lower roll changed from 590 mm to 270 mm compared with that of single straight SEN ， in favor of the remove of inclusions. As seen from temperature distribution ,the thermal center moved upward obviously and center temperature of the shell increased 6 K and 4 K respectively with the side two -furcated SEN and the side quad-furcated SEN, which contributed to the melt of mold power.
Key words: nozzle    mould    fluid flow    temperature distribution    numerical simulation    
0 前言

浸入式水口的结构对结晶器内钢液的流场和温度场分布具有重要影响[1-5].通过优化浸入式水口结构，可改善结晶器内钢液的流动状态，进而增强夹杂物去除效果、避免卷渣和提高铸坯质量[6-9].文中以邢钢大方坯连铸结晶器为研究对象，设计了直通、侧二孔和侧四孔3 种不同类型浸入式水口，利用低雷诺系数κ-ε 模型，对结晶器内流场和温度场进行了数值模拟研究.

1 结晶器内流场和温度场耦合数学模型建立 1.1 几何模型

以大方坯连铸机280 mm×320 mm 断面尺寸结晶器为研究对象，分别设计了直通式、侧二孔式及侧四孔式3 种水口，其结构如图 1 所示.表 1 给出了3 种水口的结构参数，其中定义水口侧孔向下时倾角为正.结晶器长度为800 mm, 水口浸入深度和侧孔出口上沿至钢液面距离列于表 1.为保证结晶器内钢水流动充分发展以及计算快速收敛，设置计算域为实际结晶器长度的2 倍.

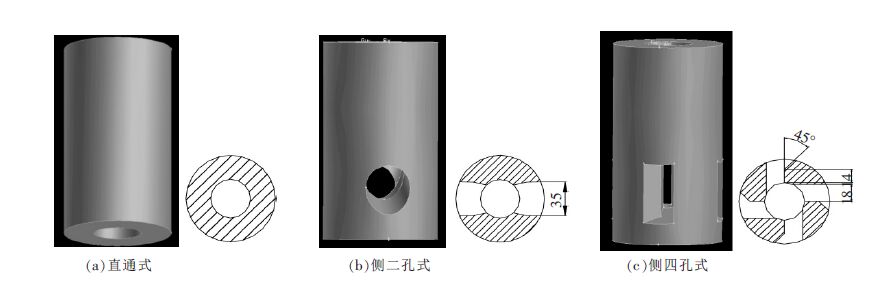图 1 水口结构以及截面图

表1 不同水口结构参数
点击放大

1.2 数学模型建立

计算流体力学软件是专门用来进行流场分析、流场计算、流场预测的软件.Fluent 流体力学软件适用于各种可压和不可压流体的计算.

用Fluent 软件包一般都要用到3 大部分软件：前处理软件、求解器、后处理软件.前处理软件主要是创建几何模型并对几何结构进行网格划分，求解器主要是导入网格模型、提供计算的物理模型、确定材料的性质、施加边界条件、完成计算和后处理.文中使用后处理软件为Tecplot 观察流体计算的结果.

根据结晶连铸器内的钢液流动特征和研究目的，使用Fluent 流体力学软件建立数学模型，为了获得结晶器内稳态浇注时钢水流体的流场和温度场，采用以下假设：

（1）结晶器内的钢液为不可压缩的黏性流体，按均相介质处理；

（2）结晶器钢液上方为自由液面，忽略保护渣的影响；

（3）不考虑结晶器震动与弧度等因素的影响；

（4）忽略凝固过程对结晶器内钢液流动的影响.

1.2.1 基本方程

基于上述模型中结晶器钢水流动呈稳态，湍流流动过程的数学描述需要的微分方程[10]、连续性方程，如式（1）所示.

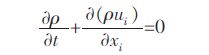
(1)

动量方程（N-S 方程）如式（2）所示：

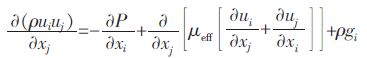
(2)

其中：μeff = μ0 + μt = μ0+ ρCμK2 / ε

能量方程如式（3）所示：

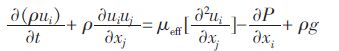
(3)

标准K-ε 双方程湍流模型，如式（4）、式（5）所示.

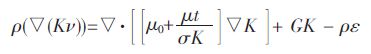
(4)
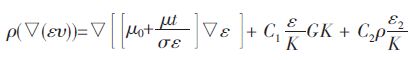
(5)

式（4）、式（5）中：μeff为有效粘度；ρ 为流体密度；t 为时间，μi为速度分量，m/s； xi为方向分量；gi为重力加速度，m/s2；κ 和ε 分别为湍动能和湍动能耗散率；GK表示由层流梯度产生的湍流动能；p 为压力；σk, σε分别为k 方程和ε 方程的湍流Prandtl 数；C1，C2为常数；μ0为层流黏度；μt为湍流黏度.

1.2.2 边界条件

（1）水口入口边界条件：入口物质为钢水，温度为1803 K，给定入口速度，其速度由拉速根据流量平衡计算得出，入口湍动能κin和耗散能ξ 根据半经验公式计算得出，κin=0.01υiN2，ξ=2κ3/2/d.其中d 为水口内径，mm.

（2）水口出口边界条件：出口物质为钢水，给定出口速度，其大小为拉速0.85 m/min, 方向为拉速方向.

（3）壁面边界条件：结晶器采用无滑移壁面，壁面附近的黏性流体采用标准壁面函数进行处理.由于不考虑凝固对钢水流动的影响，结晶器壁面温度设定为液相线温度1773 K.

（4）自由液面：钢水上方为保护渣，其散热率设为-10000 W/m3.

1.2.3 数值求解方法

基于商业软件平台，采用有限体积法对控制方程进行离散化处理，速度校正采用基于交错网格的 Simple 算法.

采用Gambit 软件构建模型的四-六面体混合网格，在水口附近流体流动敏感区域采用四面体细网格，而其它流体变量变化缓慢的区域采用六面体网格.图 2 为侧四孔式水口的网格划分及物理模型边界条件，其中Z 方向为拉坯方向.

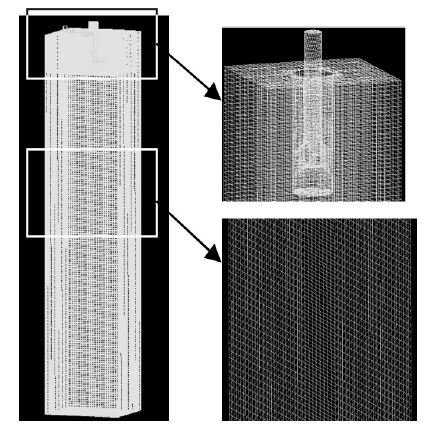图 2 侧四孔式水口结晶器物理模型及网格划分

2 结果与讨论 2.1 不同类型水口对结晶器内钢水流动状态的影响 2.1.1 结晶器内钢液流动状态对比

图 3和图 4 分别为采用3 种不同类型水口时，结晶器中心截面上的速度云图和矢量图.速度云图表示流动强弱，矢量图表示流动方向，流股冲击区域内钢水平均速度大小表示钢水对坯壳的冲击强度.由图 3（a）看出，当采用直通式水口时，钢液自水口流出并迅速向下运动，中心流流股向下逐渐扩散至一定深度时形成一股回旋流并向上达到自由液面，但自由液面速度较小（仅0.02 m/s 左右），故液面波动小，有利于减少保护渣卷入.还可以看出，直通式水口条件下，结晶器竖直面上形成了大漩涡，其涡心距离液面590 mm, 冲击深度很深，不利于夹杂物的上浮和去除.由图 3（b）看出，当采用侧二孔式水口条件下，钢

图 3 不同类型水口条件下结晶器内钢水速度分布

图 4 结晶器钢水流线以及停留时间分布图

由图 3（b）看出，当采用侧二孔式水口条件下，钢液从侧孔流出后形成强大的射流冲击窄面坯壳，射流到达窄面坯壳的速度约为0.24 m/s, 冲击点距弯月面约为180 mm； 射流到达窄面后，一部分沿着坯壳向下运动，另一部分向上运动，形成明显的上回流和下回流.侧二孔式水口浇注时，流股冲击深度较直通式水口浅，给夹杂物的上浮去除创造了有利条件，还可以增加液面活跃程度，防止结壳[11].

由图 3（c）可以看出，钢液从水口的四侧孔出来后，形成四股射流冲击窄面和宽面坯壳.部分射流交叉，进入结晶器下部.坯壳附近钢液的速度0.09 m/s左右，并形成向下和向上两个回流.侧四孔式水口下回流中心位置进一步提升，对坯壳的冲击强度明显减弱，利于坯壳的均匀生长.由结晶器弯月面和水口出口处及弯月面下400 mm 处的横截面速度矢量图可以看出，钢水可以在结晶器内形成水平旋流，该水平旋流将有利于等轴晶生长[12].

与直通式水口相比，侧四孔水口出口钢液流股冲击深度明显变小，自下部回流中心距液面距离由590 mm 减少到270 mm, 水口出口流股向下的冲击深度变小，因而有利于夹杂物上浮.直通式水口的自由液面处的流速很小，约为0.02 m/s ，故液面波动较小；而侧四孔式水口的自由液面处的流速为0.06 m/s.

2.1.2 结晶器内钢液流线及停留时间对比

图 4为3 种水口条件下结晶器内钢水流线以及停留时间分布图.可以直观反映新鲜钢水从进入结晶器后的流动轨迹.由图 4 可知，直通式水口浇注条件下，钢水在结晶器内的行程最短，最长停留时间仅为137 s, 钢液中夹杂物在结晶器中停留时间较短.侧二孔式和侧四孔式水口的最长停留时间分别为182 s和212 s, 较直通式水口延长45 s 和75 s, 可为夹杂物的去除创造良好的物理条件.

2.1.3 结晶器钢液湍动能分布对比

图 5为结晶器Z-X 中心截面上的湍动能分布图.湍动能即流体湍流脉动动能，反应了湍流流动的强烈程度.由图 5（a）可以看出，直通式水口条件下，射流对坯壳的冲击很小，只是在结晶器出口（Z=800 mm）附近出现的上升流股对坯壳略有冲击.侧二孔式条件下，钢液从水口出来后，在冲击点上下贴近窄面坯壳的地方湍动能很大，计算所得值约为0.02 m2/s2.侧四孔式水口条件下，钢液对冲击点附近湍动能远小于侧二孔式水口，计算所得值约为0.005 m2/s2.

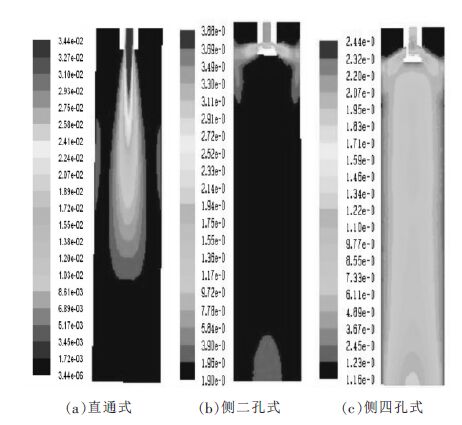图 5 结晶器Z-X 中心截面上的湍动能分布图

2.2 不同水口结晶器内钢水温度状况比较

图 6给出了3 种水口条件下结晶器宽面中心截面上弯月面以下的钢水温度分布状况.

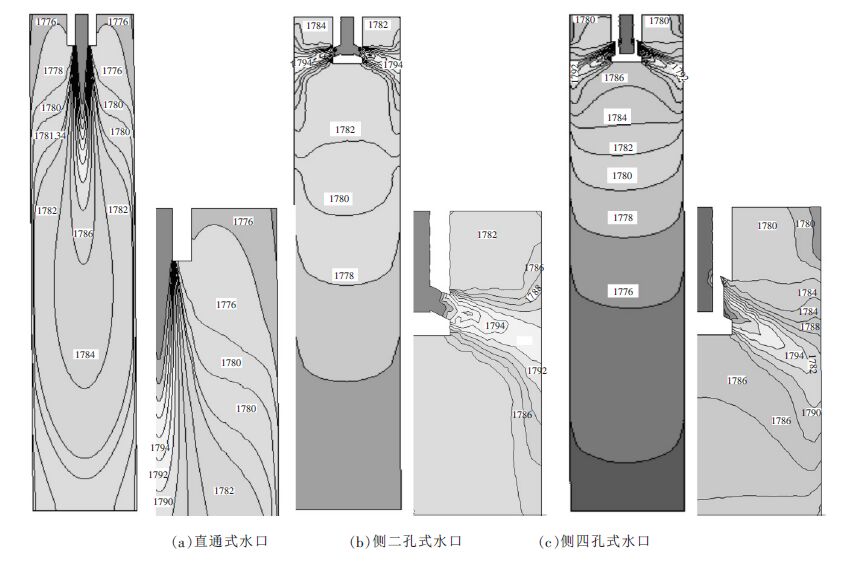图 6 结晶器宽面中心截面以及弯月面钢水温度分布

由图 6 可以看出，1803 K 的钢水从水口流出后形成射流，与周围钢液进行强烈混合和对流换热，射流附近钢液温度迅速下降.侧四孔式水口在结晶器内热中心有所上移，且高温区域范围较其它2 种条件下要大.对比弯月面处（Z=3 mm 面）的温度场可知，直通式、侧二孔式和侧四孔式水口条件下弯月面温度分别为：1776 K，1782 K 和1780 K，即相比于直通式水口，侧二孔式和侧四孔式水口的弯月面温度分别提高了6 K 和4 K，有利于保护渣熔化.

3 结论

（1）从流场来看，直通式冲击深度最大，侧二孔式次之，侧四孔式最小；侧四孔式水口在结晶器内的钢水能形成上、下两个回流，其下回流涡心较直通式水口明显上移（从590 mm 移至270 mm），有利于结晶器内初生坯壳的形成和夹杂物的上浮；此外，侧四孔式水口还能够产生较强的水平旋流，从而抑制液面波动，减小钢水死区面积.

（2）从温度场来看，侧二孔式和侧四孔式较直通式水口使结晶器内热中心明显上移，且其弯月面钢水温度比直通式分别提高了6 K 和4 K，从而有利于保护渣的熔化.

参考文献
[1] B. G. Thomas, L. J. Mika, F. M. Najjar. Simulation of fluid flow inside acontinuous slab casting machine[J]. Metall Trans B, 1990, 21(2): 387. DOI: 10.1007/BF02664206.
[2] S. Hintikka, J. Konttinen, K. Leiviska. Optimization of molen steel flow in continuous casting mold[C] // Steelmaking Conference Proceedings,1992:887.
[3] 顾武安, 唐萍, 文光华, 等. 大方坯连铸四孔浸入式水口的应用研究[J]. 钢铁, 2008, 43(4): 101–104.
[4] 王维维, 张家泉, 陈素琼, 等. 水口侧孔倾角对大方坯结晶器流场和液面波动的影响[J]. 北京科技大学学报, 2007, 29(8): 816–821.
[5] 张胤, 贺友多, 白学军, 等. 水口插入深度对连铸机结晶器内钢液流动的影响[J]. 炼钢, 2001, 17(2): 52–54.
[6] 高泽平, 苏振江. 大方坯连铸结晶器浸入式水口结构优化[J]. 炼钢, 2008, 24(2): 42.
[7] 吴狄峰. 大方坯结晶器内钢液流动 、传热 、夹杂物运动及电磁制动研究[D]. 北京:北京科技大学,2008.
[8] 李增玉, 张彩军, 关开, 等. 异型坯结晶器内钢水流动和凝固过程的耦合数值模拟[J]. 江西冶金, 2009, 17(1): 11–13.
[9] 邓南阳, 金友林. 304 不锈钢板坯连铸结晶器水口结构优化的数值模拟[J]. 特殊钢, 2010, 31(3): 10–13.
[10] 干勇, 仇圣桃. 连续铸钢过程数学物理模拟[M]. 北京 : 冶金工业出版社 , 2001.
[11] 孙海波, 韩占光, 钱宏智, 等. 注流方式对大方坯连铸结晶器内钢水流动与温度状态的影响[J]. 北京科技大学学报, 2010, 32(9): 1131–1137.
[12] K. Frauenhuber. 奥钢联不锈钢连铸技术的最新发展[J]. 钢铁, 2001, 36(4): 27–30.