| 基于FLAC3D的下向进路胶结充填采场参数研究 |
2. 江铜集团武山铜矿,江西 瑞昌 332204;
3. 钨资源高效开发及应用技术教育部工程研究中心,江西 赣州 341000
2. Jiangxi Copper Corporation Co. Ltd., Ruichang 332204, China;
3. Tungsten Resources Efficiency Development and Application Research Center of the Ministry of Education, Ganzhou 341000, China
尾砂胶结充填技术在我国应用至今已有50年的历史,尤其在金属矿山应用最为广泛[1].该采矿方法回采断面尺寸的确定是较为普遍的问题,为此进行了大量研究,其中以数值模拟计算为研究方法的占较大的比例.文献[2]采用二维有限元弹塑程序对3个断面尺寸下进路稳定性进行了研究,提出以破坏系数、应力、位移作为优化方案的参考指标,从而确定各断面尺寸的优劣.文献[3]应用虎克-布朗准则在下向尾砂胶结充填法的矿山采用应力位移为参考标准对比分析了4个断面尺寸下采场稳定性,从而确定合理的进路断面尺寸.但缺乏采用塑性区的变化作为采场稳定性参考标准的数值模拟研究,借助FLAC3D有限差分软件模拟分析了不同跨度和高度下采场应力应变和位移变化,并在此基础上,采用顶板塑性区为评价采场稳定性的一项重要指标,为矩形断面尺寸的确定提供可靠的依据.
江西某铜矿,矿体长1600 m,似层状产出,倾向165°,倾角56~64°.矿体厚度一般5~30 m,平均16.8 m,采用下向进路式尾砂胶结充填法开采矿石,现回采标高约为-200 m,上部充填体高度约为100 m,设计回采断面尺寸4 m×3 m,进路分上、下两步骤进行充填,上半部分充填体的灰砂比为1: 8,下半部分充填体的灰砂比为1: 4,为了满足扩产要求,需对进路断面进行合理扩大[4].采用FLAC3D数值模拟软件进行了不同断面尺寸下采场稳定性模拟研究,提出了顶板失稳临界的断面尺寸,对现场具有一定指导意义[5].
1 模型的建立 1.1 计算模型数值模拟研究分两部分进行:①进路高度固定,不同跨度下采场数值模拟研究;②进路垮度固定时,不同高度下采场数值模拟研究.数值模拟的可靠程度一定程度上取决于所建立的计算模型[6].为了使模拟结果更加符合实际,建立三维模型,模型分上、中、下3部分,上部充填体厚30 m,下部矿体厚29 m,中间位回采分层,矿体厚度为进路长度,根据现场取为20 m.模型整体:长×高=66 m×66 m,采场参数范围在3 ~7 m内选取.经验显示:局部开挖对其周围3~5 m范围内有影响,因此建立的模型是合适的.
为了缩短建模时间,提高模型精密度,利用ANSYS有限元软件建立三维模型并按照从模型外边界到进路逐渐加密的单元划分原则划分网格单元,再通过ANSYS TO FLAC3D软件将建好的模型导入FLAC3D中.共划分为136236个单元,24392个节点,如图 1.
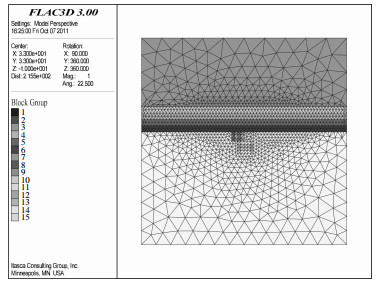 |
| 图 1 计算模型 |
1.2 本构模型和边界条件
数值模拟涉及到的岩石、充填体均属于弹塑性材料,可采用能考虑剪切破坏并直观显示主应力的Mohr-Coulomb屈服准则,Mohr-Coulomb准则的剪切破坏判据如式(1)、式(2)所示.
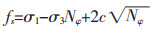
|
(1) |
其中,
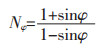
|
(2) |
式(1)中:σ1、σ3分别为最大主应力、最小主应力,c、φ分别为材料内聚力、内摩擦角.fs为破坏判断系数,当fs≥0时,材料处于塑性流动状态;当fs≤0时,材料处于弹性变形阶段[7].
模型底面和侧面约束法向位移;计算收敛准则为不平衡力比率≤10-5.模型的垂直压应力,按进路上覆岩体的自重考虑.根据充填体作用机理,充填体具有应力隔离和转移的作用,在下向回采中段的垂直方向,对于第一分层(上覆岩层与充填体接触的那个分层),由于其与上覆岩层接顶,因而上覆岩层应力最大;之后,由于充填体应力隔离和转移,到第五及以后分层,基本不受上覆岩层的应力作用[8].因此以30 m高的充填体产生的自重场作为垂直方向的初始应力场是比较合理的.
1.3 物理力学参数通过现场取样和室内岩石力学试验以及相应的岩体参数工程处理,将Mohr-Coulomb屈服准则所涉及到的计算参数列表 1.
| 表 1 模拟材料物理力学参数 |
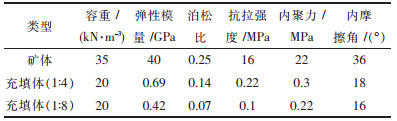 |
| 点击放大 |
2 不同跨度下数值模拟分析
进行数值模拟目的是为了得到开挖后采场稳定性情况,因此在模拟过程中将回采的分条设置成一步开挖即可,即设置为空单元.在对跨度进行研究分析时,固定进路高度为3 m,跨度3~7 m.
2.1 应力分析选取跨度6 m、7 m下进路开挖后模拟结果进行显示,采场最大主应力分布云图见图 2,采场最小主应力分布云图见图 3.通过对不同跨度下采场应力变化情况的模拟,得到以下结论:
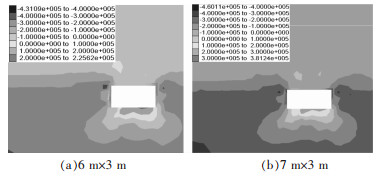 |
| 图 2 跨度6 m、7 m下采场最大主应力分布 |
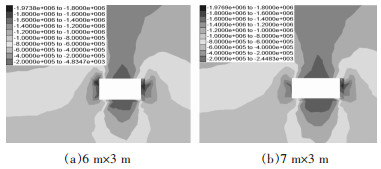 |
| 图 3 跨度6 m、7 m下采场最小主应力分布 |
(1) 上一分层充填体顶板受拉应力的控制,拉应力随着跨度的增加而增大.跨度小于5 m时拉应力基本在0.02~0.08 MPa;当跨度为6 m时顶板拉应力值≤0.1 MPa,接近充填体抗拉强度值,说明顶板处于临界稳定状态;当跨度为7 m时顶板拉应力范围0.1~0.2 MPa,达到充填体抗拉强度值,此刻作用在进路跨度范围内的充填体载荷使跨度范围以外的充填体产生斜向进路的拉伸应力,采场破坏形式主要为顶板垮落.
(2) 最小主应力集中区域主要分布在进路两侧帮,局部出现应力尖角,压应力区的分布状况随跨度增加基本不产生变化,压应力值随跨度的增加而增大,但变化幅度较小.跨度为6 m时压应力最大值为1.973 MPa,跨度为7 m是压应力最大值为1.977 MPa,这远远没有达到充填体抗压强度,说明采场受压应力影响并不大.
2.2 塑性区理论与实践都已证明,巷道围岩塑性区大小是评价围岩稳定性的重要依据和巷道支护定量设计的理论基础[9],充填体塑性区的变化与充填破坏有直观的联系[10].图 4为不同跨度下采场塑性分布,可以得到以下结论:
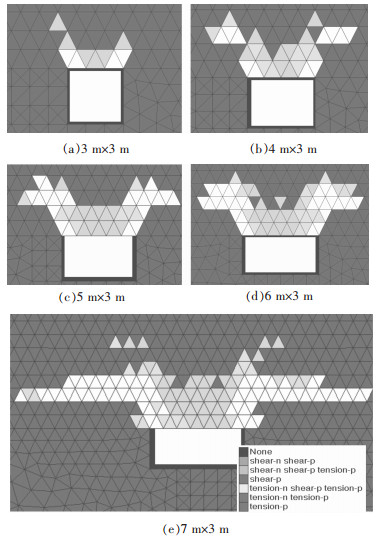 |
| 图 4 不同跨度下塑性区 |
(1) 进路开挖后塑性区呈“V”字形主要分布在上一分层顶板充填体上,尤其以顶板两尖角处最密集,垮度较小时,进路上部第二分层及以上基本无塑性区,这说明直接顶板充填体的稳定性决定了进路的稳定性,这是符合实际的.
(2) 随着跨度的增加,塑性区面积也逐渐增大.当垮度为6 m时,上一分层顶板充填体的塑性区范围达到了4/5,说明顶板充填体破坏较为严重;当垮度为7 m时,直接顶板充填体全部处于塑性变形状态,说明此刻采场已经处于很危险的状态.
将塑性区面积统计(见表 2)并进行曲线拟合(见图 5),从曲线可以看出跨度不超过6 m时,塑性区面积与跨度基本呈线性关系,当跨度超过6 m后塑性区急剧增加,在跨度为7 m时塑性区囊括了跨度范围内的上一分层顶板充填体,这也验证了跨度7 m时顶板处于失稳状态.
| 表 2 不同跨度塑性区范围 |
 |
| 点击放大 |
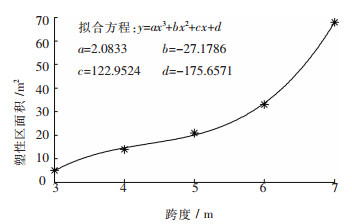 |
| 图 5 跨度与塑性区面积的关系 |
2.3 位移分析
图 6为跨度分别为6 m、7 m下顶板竖直方向位移分布情况,图 6中深色部分位移值较大,可见进路上部顶板的位移最大,在顶板充填体上,跨度5倍距离范围内均有一定的影响,超过5倍的距离进路的开挖对位移的影响不大,符合实际情况.顶板最大位移随着跨度的增加而变大,当跨度6 m时顶板最大位移9.2822 mm,当跨度7 m时,顶板最大位移值13.007 mm,前述分析表明跨度为6 m时采场基本达到失稳临界状态,跨度为7 m采场已经处于失稳状态,因此可以把跨度为6 m下顶板最大位移作为采场临界失稳的预测参数标准,这对现场具有指导意义.
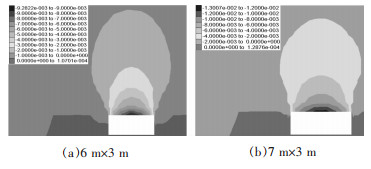 |
| 图 6 跨度6 m、7 m下顶板竖直方向位移分布 |
3 不同高度下数值模拟分析
为了研究进路高度与采场稳定性关系,模拟开挖跨度5 m、高度3~7 m时进路的开挖,根据模拟目的,同样将进路设置为空模型.
3.1 应力分析通过对不同高度下采场应力分布的模拟,得到下述结论:
(1) 随着高度的增加,进路开挖后采场最大主应力分布基本无变化:顶板受拉应力的控制,拉应力值小于充填体抗拉强度.跨度变化幅度3~7 m内最大拉应力值变化幅度为0.01 MPa,鉴于篇幅有限,只将跨度3~5 m下采场最大主应力分布列出,见图 6.
(2) 图 7为不同高度下采场最小主应力分布.可以看出,随着跨度的增加最大压应力值有所增大,但幅度很小;压应力集中区域没有变化:位于进路两侧帮及上下两尖角处.
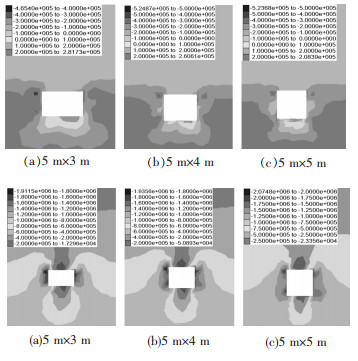 |
| 图 7 高度3-5 m下采场最小主应力分布 |
3.2 塑性区
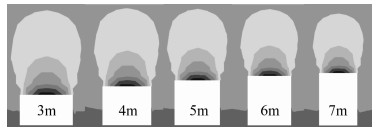
不同高度下采场塑性区分布如图 8,从图 8中可以看出随着高度的增加塑性区基本没有变化,说明塑性区与高度关系较小,进路高度在3~7 m范围内变化时,塑性破坏的面积没有明显变化.
 |
| 图 8 不同高度下塑性区 |
3.3 位移分析
图 9为不同高度下进路顶板竖直方向位移云图.从图 9中可以发现,进路高度对进路开挖后采场的位移分布影响较小,采场竖直方向最大位移区位于进路顶板中间;采场竖直方向最大位移值同样也没有太大变化,当进路高度从3 m增大到7 m的过程中,位移最大值波动幅度仅为0.02 mm.
 |
| 图 9 不同高度下竖直方向位移 |
4 结论
针对采用下向尾砂胶结充填法的矿山,在没有竖筋支护的情况下,通过本文研究得到充填采场稳定性与矩形断面尺寸的关系:
(1) 进路高度在3~7 m变化时对采场稳定性影响不大,可根据采矿设计、机械水平灵活把握.
(2) 矩形进路充填体顶板破坏以拉应力破坏为主,剪切破坏面较小.
(3) 跨度为6 m时顶板处于失稳临界状态.
| [1] |
王新民, 肖卫国, 张钦礼.
深井矿山充填理论与技术[M]. 长沙: 中南大学出版社, 2005.
|
| [2] |
王永智. 上向进路式尾砂胶结充填采矿法采场结构参数优化研究[D]. 昆明: 昆明理工大学, 2005.
|
| [3] |
李海港. 下向分级尾砂胶结充填采场结构参数优化试验及数值模拟[D]. 赣州: 江西理工大学, 2007.
|
| [4] |
段龙银, 彭小刚. 武山铜矿下向胶结充填试验方案探讨[J].
铜业工程, 2007(1): 11–13.
|
| [5] |
肖猛, 丁德馨, 莫勇刚. 软岩巷道围岩稳定性的FLAC3D数值模拟研究[J].
矿业研究与开发, 2007, 27(1): 73–75.
|
| [6] |
刘晓明, 罗周全, 张保. 上向分层回采采场稳定性数值模拟研究[J].
矿冶工程, 2009, 29(4): 10–13.
|
| [7] |
赵延林, 吴启红, 王卫军, 等. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J].
岩石力学与工程学报, 2010, 29(7): 1424–1434.
|
| [8] |
刘同有.
充填采矿技术与应用[M]. 北京: 冶金工业出版社, 2001.
|
| [9] |
翟所业, 贺宪国. 巷道围岩塑性区的德鲁克-普拉格准则解[J].
地下空间与工程学报, 2005, 1(2): 223–226.
|
| [10] |
周爱民.
矿山废料胶结充填[M]. 北京: 冶金工业出版社, 2007.
|
 2011, Vol. 2
2011, Vol. 2

