| 基于位移反分析的岩质边坡稳定性分析 |
b. 江西理工大学 建筑与测绘工程学院, 江西 赣州 341000
b. School of Architectural and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
边坡稳定性的问题涉及到矿山工程、公路工程、水利水电工程等多个领域,边坡失稳带来的灾害每年都给人们的生命财产安全带来重大损失,因此,边坡失稳(滑坡)已成为三大灾害之一[1].对于边坡稳定性的研究一直是边坡工程研究的重要内容,在矿山工程中,以露天开采方式进行采矿的露天矿,随着开采时间的延长就形成了一定规模露天边坡.而这些露天边坡的稳定性直接关系到矿山的正常生产,是矿山安全生产的重要制约因素,所以对露天矿边坡稳定性的研究具有重要的现实意义.
在进行边坡稳定性分析时,需要使用到岩土体的物理力学参数,而这些参数选取的准确程度都影响着边坡稳定性分析结果的正确性.目前,获取岩土体各种参数的传统方法主要有实验法、专家经验法、类比法等.大量工程实践表明,由于实际现场的边坡岩土体受到多种因素的共同控制,因此现场边坡岩土体的各种参数与传统方法所得的各种参数存在一定的误差[2].人们为了获得与实际现场边坡岩土体参数更接近的数据,提出了位移反分析的方法.位移反分析方法,就是通过对工程现场进行监测得到边坡岩土体的位移量信息,并将其作为已知条件,通过相应的数值模型和和数值计算方法反推出岩土体的物理力学参数的一种方法.随着有限元等数值计算的发展,位移反分析法已得到越来越广泛的应用和发展[3-4].
利用BP神经网络的仿真预测功能,结合粒子群算法的全局寻优特性,编制了位移反分析程序,并针对某露天矿边坡的现场实际特点,进行位移反分析得到了岩土体反演参数的结果,最后采用FLAC3D有限差分软件计算出边坡的安全系数,为此分析了露天矿边坡的稳定性.
1 粒子群算法与BP神经网络 1.1 粒子群算法的基本原理粒子群优化算法(PSO)是由美国的Eberhar博士和Kennedy博士于1995年提出的一种通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法.采用速度-搜索模型,在可行解空间中随机初始化一群粒子并赋予初始位置和速度, 每个粒子都为优化问题的一个可行解,并由目标函数为之确定其适应度值.然后通过反复迭代搜索最终得到最优解.在每一次迭代过程中,粒子将记录个体最优位置(pbest)和全局最优位置(gbest)2个极值,并以此来更新自己.粒子在找到上述2个最优位置后,根据以下公式来更新自己的速度和位置:
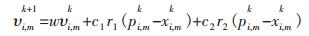
|
(1) |
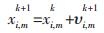
|
(2) |
式(1)、式(2)中:υi, mk是第i个粒子在第k次迭代之后、第m维度上的速度;r1,r2为2个独立的随机数,都服从[0, 1]均匀分布;Pi, mk是第k次迭代之后粒子i的个体最优在第m维的位置;xi, mk是第k次迭代之后全局最优在第m维的位置;第i个粒子在第k次迭代之后、第m维的位置;c1和c2是算法的加速系数(或称为学习因子),通常为正常数;w为惯性权重系数,通常在[0.8, 1.2]之间取值[5-6].
1.2 BP神经网络的基本原理在神经网络模型中,最有代表意义和广泛应用的就是BP神经网络模型,BP神经网络是1986年由美国Rumelhart和McCelland为首的科学家小组提出,是一种多层前馈神经网络.这种网络的主要特点是信号前向传递,误差反向传播.在信号前向传递的过程中,输入信号从输入层经隐含层逐层处理直至输出层,每一层的神经元状态只影响下一层的神经元状态.如果输出层得不到期望值输出,则进入反向传播过程,根据预测误差信号沿原来的连接通路返回,调整各层间的权值和阀值,逐次地向输入层传播.通过不断反复运用减小误差,使网络的输出不断趋近于期望输出.一般传递函数采用S函数BP神经网络的结构不同对问题模型的仿真预测力也不同,选择合理的神经网络结构对预测结果的准确性有直接影响[7].
2 位移反分析法操作步骤 2.1 采用粒子群算法优化BP神经网络结构采用BP神经网络可以建立待反演参数与岩土体位移之间的映射关系,得到一个结构、权值、阀值确定的BP神经网络模型.为了使神经网络能够更好的预测输出,利用粒子群算法的随机搜索全局寻优功能,对BP神经网络的初始权值、阀值进行优化,从而得到更佳的各个权值、阀值.遗传算法优化BP神经网络结构的具体实现过程如下:
(1) 初始BP神经网络结构,结合具体情况,设定网络的输入层、隐含层、输出层的层数和神经元个数.
(2) 设定种群的规模、维度,在允许范围内随机产生每个粒子的初始速度和位置.种群的规模, 结合具体问题确定, 通常情况下取为几十个到百个以上; 粒子维度=输入层至隐含层的连接权值个数+隐含层至输出层的连接权值个数+隐含层的阈值个数+输出层的阈值个数;粒子的速度及位置,在取值范围内, 随机赋于初始值.
(3) 确定粒子群算法的目标函数,计算出每个个体的适应度值.本文采用的目标函数是残差最小平方和函数,即
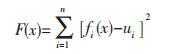
|
(3) |
式(3)中:n为测点个数;fi(x)为第i个测点的计算位移;ui为第i个点的实测位移.
(4) 比较计算出的适应度值,确定每个粒子的个体极值点和全局最优极值点.若present<pbest,则pbest=present,pbest=xik;否则,pbest不变;若present<gbest,gbest=present,gbest=xik;否则,gbest不变;其中:present为当前粒子的适应度,pbest为粒子的个体极值,gbest为全局最优值.
(5) 更新每个粒子的速度和位置.根据惯性权重粒子群公式(1)、(2)更新粒子的速度和位置, 并且考虑更新后的速度和位置是否在限定的范围内.速度更新:若υik+1>υmax,则υik+1=υmax;若υik+1<υmin,则υik+1=υmin;位置更新:若xik+1>xmax,则xik+1=xmax;若xik+1<xmin,则xik+1 =xmin.
(6) 若迭代次数达到最大迭代次数或满足式(3)误差精度要求,则算法收敛.最后一次迭代的全局最优值gbest即为我们所求的值.
(7) 把全局最优值gbest赋给BP神经网络的权值和阀值,得到优化后的神经网络结构.
2.2 采用粒子群算法进行参数反分析将建立的神经网络优化之后,对于任意给定的一组反演参数,可以通过网络的预测能力求出其相应的位移;因此,可以通过先确定反演参数的取值范围,再利用遗传算法的全局寻优功能,对反演参数进行搜索,最后得到最佳的反演参数数值.
应用神经网络和粒子群算法进行位移反分析的步骤如下:
(1) 采用正交试验方法设计试验方案,通过FLAC3D软件对每个方案进行计算得到学习样本和测试样本.
(2) 设定种群的规模、维度.根据工程资料, 确定待反演参数的取值范围,在允许范围内随机产生每个粒子的初始速度和位置.
(3) 确定粒子群算法的目标函数,计算出每个个体的适应度值.本文采用的目标函数是残差最小平方和函数.
(4) 比较计算出的适应度值,确定每个粒子的个体极值点和全局最优极值点.
(5) 更新每个粒子的速度和位置.根据惯性权重粒子群公式(1)、(2)更新粒子的速度和位置, 并且考虑更新后的速度和位置是否在限定的范围内.
(6) 若迭代次数达到最大迭代次数或满足式(3)误差精度要求, 则算法收敛.最后一次迭代的全局最优值gbest中每一维的权值和阈值即我们所求的最佳的反演参数数值.
3 计算安全系数评价边坡稳定性由于边坡安全系数不仅原理简单而且物理意义明确,因此采用安全系数来评价边坡的稳定性状态,至今仍为边坡稳定性分析中最重要的指标和概念.严格来说,安全系数是基于极限平衡分析方法的一种评价指标,而数值模拟方法侧重于岩体破坏机理的分析,是与极限平衡方法并行的一种分析方法.在早期,两者是不存在交汇点的,直到基于数值模拟技术的强度折减法将两者联系在一起.并且随着计算机性能的提高以及各种成熟商用软件的推出,使强度折减法得到越来越广泛的应用[8].
强度折减法中对安全系数定义为:使边坡刚好达到临界破坏状态时,对岩土体的抗剪强度进行折减的程度,即定义安全系数为岩土体的实际抗剪强度与临界破坏时的折减后剪切强度的比值.它的特点是利用公式(4)和公式(5)来改变强度指标c和ϕ,然后对边坡的稳定性进行数值分析,通过不断增加折减系数,反复计算,直至达到临界破坏时得到的折减系数,即为安全系数.
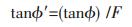
|
(4) |

|
(5) |
式中:c和ϕ为岩体材料的内聚力和内摩擦角;c′和ϕ′为经过折减后的内聚力和内摩擦角;F为折减系数.
通过以上位移反分析的方法,确定边坡现场实际的岩体物理力学参数,再采用FLAC3D中的强度折减法来求解边坡的安全系数,从而评价边坡的稳定性状态.
4 工程实例分析某露天矿山地处低山-丘陵过度地带,属构造剥蚀地貌区, 山坡坡度一般在41.42~53.8 °之间.矿体走向长1600 m, 延深大于300 m, 矿体倾角在42~45 °之间, 属于倾斜矿体.目前,随着露天采场的开采时间延长露天采场在封闭圈72 m以上形成了东边坡、南边坡、西边坡、西北边坡4大部分边坡.研究的对象为西北边坡:边坡坡顶高程136 m,目前坡脚高程72 m,坡高约64 m,边坡走向约60 °,总体坡度约40 °.目前共有5个台阶,台阶高度约12 m,平台宽5~8 m,台阶坡度约80~90 °.边坡岩体主要以绢云母千枚岩为主,间夹砂质千枚岩和团块状、透镜状、条带状石英体,片理发育,构造裂隙不甚发育.边坡上部为全风化带,千枚岩全部变色,光泽消失,岩石的组织结构完全破坏,已崩解和分解成松散的土状或砂状态,厚度约5~ 10 m;边坡下部为弱风化带,千枚岩大部分褐红色,少部分呈灰色,岩石基本保持了原始组织结构,大量岩石沿片理面剥落.
为了对该边坡采用位移反分析方法得到岩体物理力学参数值, 在该边坡上选定位移监测点监测位移量的变化,并且将监测的数据记录.
4.1 位移反分析确定反演参数值 4.1.1 神经网络样本的构造(1) 采用正交试验设计方法设计试验方案,其中试验因素为粘聚力c和内摩擦角ϕ,每个因素分为4个水平.根据工程资料,确定待反演参数的数据取值范围分别为粘聚力c:0.1~1.0 MPa,内摩擦角ϕ:18~30 °.
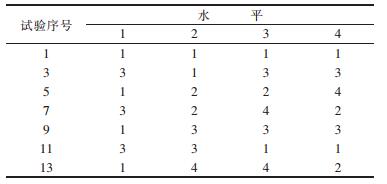
(2) 根据试验含有2个试验因素、4个水平,采用正交表L16(45)进行正交试验设计来确定试验样本,部分正交表如表 1所示[9]:
| 表 1 正交表 |
 |
| 点击放大 |
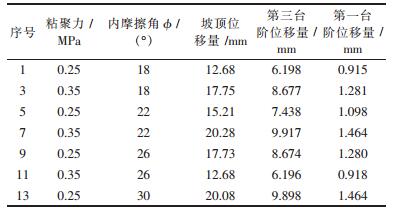
(3) 对正交表L16(45)将各试验因素的水平进行组合得到试验方案,采用数值计算软件FLAC3D计算各试验方案下监测点的位移量,由此得到16个神经网络的训练样本.部分训练样本如表 2所示[9]:
| 表 2 神经网络训练样本 |
 |
| 点击放大 |
4.1.2 优化神经网络结构
建立好待反演参数与岩土体位移之间映射关系的BP神经网络,再采用粒子群算法对BP神经网络进行优化.首先,确定BP神经网络为一个隐含层,设定输入层为2个节点,经过对隐含层节点数进行分析和比较, 对于有m个输入节点的BP神经网络,取(2m+1)个隐含层节点可在网络容量和训练时间之间取得较好的折中,故确定隐含层为5个节点,输出层为1个节点数,得到初始的BP神经网络模型.然后,采用粒子群算法根据2.1的步骤对BP神经网络进行优化得到一个结构、权值、阀值更佳的BP神经网络模型.
4.1.3 进行参数反分析根据有关文献及现场经验表明,对于边坡位移监测位置的选取,监测点必须选择在临界滑移线以内.临界滑移线在坡脚以上的微小距离内穿过坡面,因此,在未知滑移线位置的情况下,选取坡脚作为监测点是不合适的.但是坡顶位置一定在临界滑移线以内,故坡顶位置是一个很好的监测位置.而对于位移监测方式的选择,无论是监测边坡水平位移、边坡竖直位移还是边坡总位移都可作为监测的位移方式[10].本边坡共布置3个监测点,分别布置在坡顶位置,第3台阶位置和第1台阶位置.根据现场边坡位移监测的数据分别是坡顶位移量:16.864 mm、第3台阶位移量:8.466 mm、第1台阶位移量:1.197 mm,输入反演参数的取值范围,用粒子群算法的全局寻优功能,使目标函数计算结果最小的个体即为参数最佳的反演参数最优解.
经过反分析搜索出岩体粘聚力c和内摩擦角ϕ的最优值,参数反演结果粘聚力c值为0.518 MPa,内摩擦角ϕ值为27.455°.
4.2 边坡稳定性分析根据4.1位移反分析确定的反演参数结果,利用FLAC3D中的强度折减法求解出西北边坡的安全系数为1.374,表明该边坡是处于稳定状态的.判断结果与现场边坡的实际状态吻合.
5 结论利用BP神经网络的仿真预测功能,结合粒子群算法的全局寻优特性,对岩质边坡进行了位移反分析, 并通过计算安全系数分析了边坡的稳定性,主要结论如下:
(1) 利用了神经网络的非线性映射、仿真预测功能,结合粒子群算法的全局寻优特性,进行位移反分析是可行的.
(2) 待反演参数的变化范围对位移反分析程序的计算收敛速度影响很大,变化的范围愈小,收敛速度就越快.
(3) 根据位移反分析得到的岩体物理力学参数数值,对边坡的稳定性进行评价,其结果更准确与现场更吻合.
| [1] |
郑颖人, 陈祖煜, 凌天清, 等.
边坡与滑坡工程治理[M]. 北京: 人民交通出版社, 2010.
|
| [2] |
王思敬.
中国岩石力学与工程世纪成就[M]. 南京: 河海大学出版社, 2004.
|
| [3] |
孙钧, 黄伟. 岩石力学参数弹塑性反演问题的优化方法[J].
岩石力学与工程学报, 1992, 11(3): 221–229.
|
| [4] |
喻四立. 位移反分析方法在某路堑边坡中的应用[J].
南华大学学报:自然科学版, 2005, 19(2): 74–76.
|
| [5] |
高玮. 基于粒子群优化的岩土工程反分析研究[J].
岩土力学, 2006, 27(5): 795–798.
|
| [6] |
朱珍德, 杨喜庆, 郝振群, 等. 基于粒子群优化BP神经网络的隧道围岩位移反演分析[J].
水利与建筑工程学报, 2010, 8(4): 16–20.
|
| [7] |
高隽.
人工神经网络原理及仿真实例[M]. 北京: 机械工业出版社, 2003.
|
| [8] |
彭文斌.
FLAC3D实用教程[M]. 北京: 机械工业出版社, 2008.
|
| [9] |
黄戡, 刘宝琛, 彭建国, 等. 基于遗传算法和神经网络的隧道围岩位移智能反分析[J].
中南大学学报:自然科学版, 2011, 42(1): 213–219.
|
| [10] |
林杭, 曹平, 官凤强, 等. 位移突变判据中监测点的位置和位移方式分析[J].
岩土工程学报, 2007, 29(9): 1433–1437.
|
 2011, Vol. 2
2011, Vol. 2
