2011, Vol. 2
图 1(Fig. 1)
表 1(Table 1)
基于单元安全度的露井联采边坡稳定性分析
引用本文 |
陈建平, 赵奎. 基于单元安全度的露井联采边坡稳定性分析[J]. 有色金属科学与工程, 2011, 2(5): 84-88. 
CHEN Jian-ping, ZHAO Kui. Stability analysis of slopes at an open-underground combined mine based on zone safety degree[J]. Nonferrous Metals Science and Engineering, 2011, 2(5): 84-88.
| 基于单元安全度的露井联采边坡稳定性分析 |  [PDF全文] |
1.
江西理工大学资源与环境工程学院, 江西 赣州 341000;
2. 钨资源高效开发及应用技术教育部工程研究中心, 江西 赣州 341000
2. 钨资源高效开发及应用技术教育部工程研究中心, 江西 赣州 341000
摘要：传统边坡稳定性分析方法只局限于二维的单一坡体剖面, 且最终只得到一个安全系数, 针对传统分析方法的缺陷, 引入了单元安全度分析方法, 采用FLAC3D内嵌FISH语言编写了计算单元安全度的程序, 并结合某露天地下联合开采矿山实例进行计算, 得到了该露天矿边坡单元安全度的分布.结果表明：单元安全度小于1的地方集中在东部边帮和南端帮边坡, 最小单元安全度为0.91, 出现在南端帮边坡处, 为矿山安全生产和矿石充分回采提供科学指导依据.
关键词：边坡稳定 FLAC3D 单元安全度 露井联采
Stability analysis of slopes at an open-underground combined mine based on zone safety degree
1.
Faculty of Resource and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. 2Engineering Research Center of High-efficiency Development and Application Technology of Tungsten Resources, Ganzhou 341000, China
2. 2Engineering Research Center of High-efficiency Development and Application Technology of Tungsten Resources, Ganzhou 341000, China
Abstract: The traditional slope stability analysis method is limited to only single slope body profile of two dimensions, and finally only one safety coefficient is achieved. To overcome this defect, this paper introduces the analysis method of zone safety degree, and with the help of the embedded FISH language of FLAC3D, the program of zone safety degree calculation is written, the distribution of zone safety degree in this mine is gained taking an open-underground combined mine as example. The results show that, the places with zone safety degree less than 1 are concentrated in the eastern and south sides of slope, and the smallest zone safety degree 0.91 appeared in the southern slope, which provides scientific guidance to the safe production of the mine and full recovery of the ore.
Key words:
slope stability FLAC3D zone safety degree open-underground combined mining
0 引言
3 数值计算结果分析 3.1 计算条件及过程
目前对于边坡稳定性的评价，大都是通过计算给出一个安全系数，用该系数来表征边坡的稳定程度.常用的计算方法有极限平衡法[1-3]和强度折减法[4-5]等.极限平衡法把边坡上的滑体视为刚体，利用滑体的静力平衡原理分析边坡在各种极限破坏模式下的受力状态，并以边坡滑体上的抗滑力和下滑力之间的比值定义为安全系数.强度折减法[6]则将有限元方法与强度折减结合，通过不断改变某一强度(内聚力、内摩擦角)折减系数来进行边坡的弹塑性有限元分析，并基于一定的经验判据，确定边坡达到了极限平衡状态，将由此所得到的相应强度折减系数作为边坡的安全系数.以上这些方法都局限于二维的单一坡体剖面，最终只得到一个安全系数.如在FLAC3D软件中只能显示单元是否进入塑性屈服状态，对单元接近屈服状态的程度没有定量计算和显示功能[7-9].
为此，文中定义了基于摩尔库仑准则的单元安全度，并通过FLAC3D内嵌FISH语言编写了计算单元安全度的程序，以某露天地下联合开采矿山的采场边坡稳定性分析为例，用具体每个边坡单元的安全度来定量研究该露天矿各区域的稳定状况.该方法有利于从整体上了解边坡稳定状况，掌握边坡潜在的破坏失稳位置.
1 单元安全度由于所研究的边坡破坏模式主要以沿滑面发生剪切破坏为主，本文采用摩尔-库伦模型对边坡进行稳定性分析，摩尔-库伦屈服准则的屈服函数为：
|
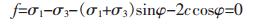
(1) |
式(1)中：σ1为第一主应力；σ3为第三主应力；c、φ，分别为内聚力和内摩擦角.
由式(1)可定义计算单元安全度I的公式：
|
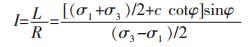
(2) |
式(2)中：I为单元安全度；L为单元接近屈服状态的程度；R为莫尔圆半径.具体如图 1所示，其中相切是临界状态.
 |
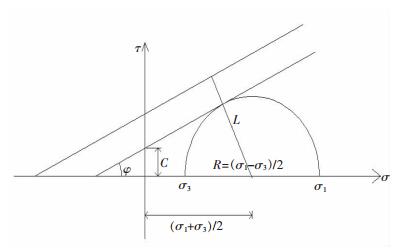| 图 1 摩尔-库伦准则 |
由式(2)和图 1可看出，当I＞1时，该单元处于安全状态；当I=1时，该单元处于临界屈服状态；当I＜1时，该单元进入塑性屈服状态.单元安全度的大小即表征单元抵抗进入塑性屈服状态的强弱.
通过FLAC3D软件内置的FISH命令可以实现读取单元的应力σ1、σ3以及单元的材料力学参数c、φ，并可通过编写FISH程序可以计算出模型中每个单元的安全度，再由FLAC3D后处理显示出来.
2 数值计算模型建立由于用FLAC3D软件前处理模块建模型比较复杂，因此，本次数值模拟分析结合AUTOCAD和大型通用有限元软件ANSYS建立模型，然后通过接口程序转化为FLAC3D的前处理数据格式，最后导入到FLAC3D软件中进行计算[10-12].
根据矿山实际情况，建立了三维变模型，模型水平、竖直长度为3560 m、580 m、纵向深度为3400 m.建模时建立了露天和地下两大部分，其中地下部分矿体倾角为70°，共建立了75344个单元，14716个节点.如图 2为三维网格模型图，图 3为隐藏露天部分矿体后的模型网格图，图 4为隐藏围岩后的露天和井下模型网格图.
 |
| 图 2 模型网格图 |
 |
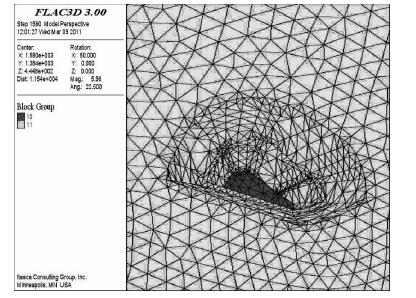| 图 3 隐藏露天采场矿体部分后的网格图 |
 |
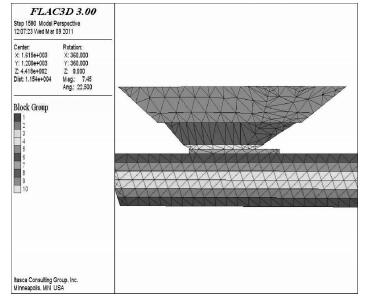| 图 4 隐藏围岩后的露天和井下矿体网格图 |
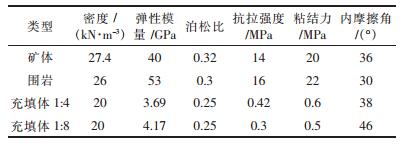
根据矿山地质资料，采用Hoek-Brown准则，选取矿岩及充填体的物理力学参数，材料的具体物理参数见表 1.
| 表 1 矿岩及充填体的物理力学参数 |
 |
| 点击放大 |
3 数值计算结果分析 3.1 计算条件及过程
计算模型顶部表面为自由边界，模型底部(z=0)设为固定约束边界，模型左右、前后四侧均施加水平方向位移约束.在初始条件中，不考虑构造应力，仅考虑自重应力产生的初始应力场.
整个模型计算过程分为3个计算工况：第1工况为自重场的计算，其中井下共有6个中段，6个中段中有4、5、6号3个中段已经回采充填，计算中直接对其赋予充填体属性，其它部分赋予矿体属性进行计算；第2工况模拟露天矿体的开挖，保存计算结果；第3工况进行单元安全度计算，首先删除已经赋空值的单元(null zone)，再利用FISH命令读取单元的应力σ1、σ3以及c、φ，依据式(2)的定义，对每个非空单元进行单元安全度计算.
3.2 塑性区分析计算结果见图 5至图 8，其中为方便观察边坡内部塑性区情况，在沿着矿体走向和垂直矿体走向做两个切片图，如图 7、图 8.图 5、图 6表明由于井下充填体力学参数低，整个露天边坡存在向下挤压充填体的态势，剪应变增量集中在边坡顶部和坡脚位置.从图 7和图 8的边坡切片图可以发现，两切片塑性区几乎贯通坡面，但从图 6中反映出道剪应变增量只是在露天边坡坡顶的位置比较集中，并没有贯穿整个坡面.
 |
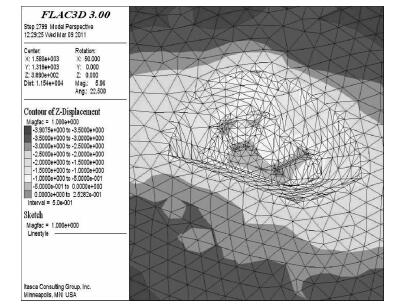| 图 5 第2工况后的竖向位移场 |
 |
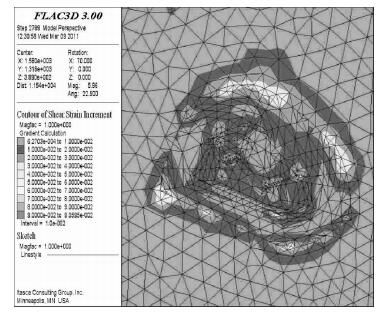| 图 6 第2工况后的剪应变增量云图 |
 |
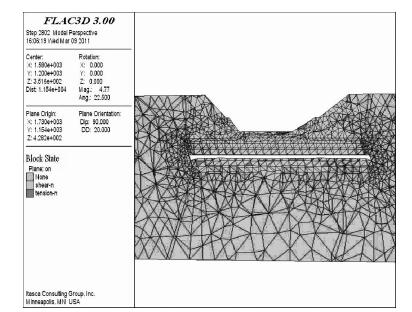| 图 7 沿矿体走向剖面塑性区云图 |
 |
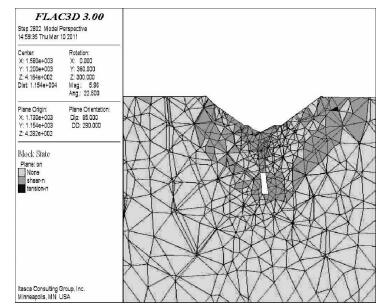| 图 8 垂直矿体走向剖面塑性区云图 |
为整体了解边坡稳定状况，掌握边坡潜在的破坏失稳位置，同时为达到具体了解每单元抵抗进入塑性屈服状态强弱的目的，有必要通过单元的安全度计算来定量研究该露天矿各区域的稳定状况.
3.3 单元安全度分析在工况2之后，导入边坡单元安全度计算程序重新计算，在沿矿体走向和垂直矿体走向相同的切片位置考察露天开采对坡体稳定性的影响.图 9为工况二后各剖面的单元安全度云图；为研究边坡最危险位置，通过FLAC3D软件后处理功能，设置显示单元度大小的范围，在切片上显示出所有单元安全度小于1的单元，如图 10所示.其中黄色区域均为单元安全度小于1的单元部位，这表明在露天开采过程中，东部边帮和南端帮边坡(黄色区域)不仅大部分进入塑性区状态，并且在该区域出现单元安全度小于1集中的情况，说明该区域的单元接近屈服状态的程度L小于莫尔圆半径R，极易出现破坏现象.
 |
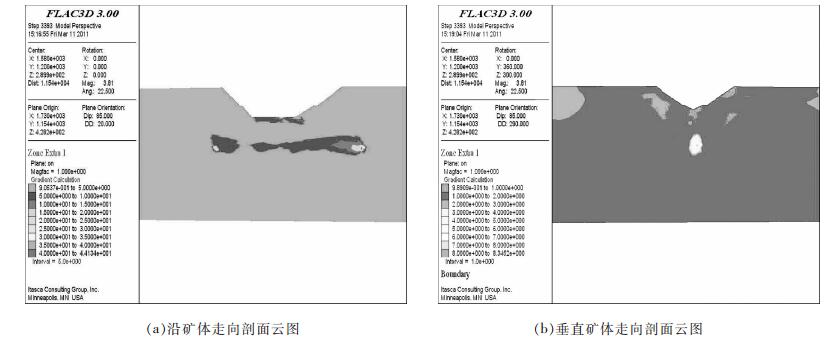| 图 9 第2工况后剖面的单元安全度云图 |
 |
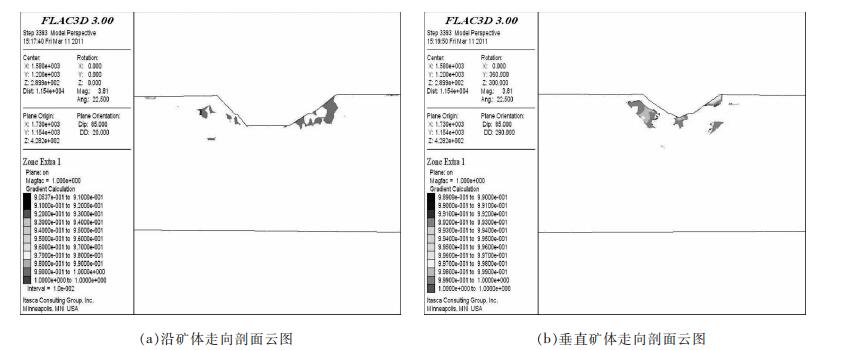| 图 10 第2工况后剖面上单元安全度小于1的部分 |
由以上分析结果表明，综合考察单元安全度的大小和塑性区的分布可对边坡的总体稳定状态进行判断，通过分析边坡单元安全度小于1的区域的塑性区分布，如果该区域的塑性区已经跟软弱岩层贯通，则边坡极易发生失稳.
同时，通过分析模拟结果，第2工况后，沿矿体走向方向的剖面露天边坡的速度矢量场开始剪出，但剪应变增量云图并没有贯通坡面，尽管露天开采使得坡体表面出现了一些塑性区几乎完全贯通的区域，但这些地方的单元安全度还处于大于1的状态，因此边坡仍然处于稳定状态，但是此时塑性区贯通，也表明边坡处于屈服状态，对该部分区域边坡也要采取相应的稳定性处理.
4 结论(1) 与传统方法相比，单元安全度分析方法适用于立体边坡模型，可得到每个单元安全系数等优点；
(2) 将单元安全度分析方法应用到某露井联采实例，定量研究该露天矿各区域的稳定状况，表明开采后，矿山最危险的地方出现在单元安全度小于1的地方集中在东部边帮和南端帮边坡.
参考文献
| [1] |
蔡美峰, 何满潮, 刘东燕.
岩石力学与工程[M]. 北京: 科学出版社, 2002: 379-392.
|
| [2] |
陈祖煜, 汪小刚, 杨健, 等.
岩质边坡稳定分析:原理、方法、程序[M]. 北京: 中国水利水电出版社, 2005: 373-399.
|
| [3] |
陈祖煜. 土力学经典问题的极限分析上、下限解[J].
岩土工程学报, 2002, 24(1): 1–11.
|
| [4] |
赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J].
岩石力学与工程学报, 2003, 22(2): 254–260.
|
| [5] |
郑颖人, 陈祖煜, 王恭先, 等.
边坡与滑坡工程治理[M]. 北京: 人民交通出版社, 2007.
|
| [6] |
刘金龙, 栾茂田, 赵少飞, 等. 关于强度折减有限元方法中边坡失稳判据的讨论[J].
岩土力学, 2005, 26(8): 1345–1348.
|
| [7] |
沈可, 张仲卿. 三维抗滑稳定分析中的点安全系数法[J].
人民珠江, 2003(2): 21–22.
|
| [8] |
刘波.
FLAC原理、实例与应用指南[M]. 北京: 人民交通出版社, 2005.
|
| [9] |
陈育民, 徐鼎平.
FLAC/FLAC3D基础与工程实例[M]. 北京: 水利水电出版社, 2009.
|
| [10] |
HOEK E, BRAY J.
Rock slope engineering[M]. London: Institute of Mineral and Metallurgy, 1981: 309.
|
| [11] |
蓝航. 基于FLAC3D的边坡单元安全度的分析与应用[J].
中国矿业大学学报, 2008, 37(4): 570–574.
|
| [12] |
姜谙男, 曾正文, 唐春安. 岩芯成饼单元安全度三维数值试验及地应力反馈分析[J].
岩石力学与工程学报, 2010(8): 1610–1617.
|