| 失配性质对二维失配铝膜结构及位错形成的影响 |
2. 江西理工大学应用科学学院,江西 赣州 341000
2. School of Applied Science, Jiangxi University of Science and Technology, Ganzhou 341000, China
异质外延生长薄膜晶体已经广泛应用于许多信息功能材料和器件.由于外延生长的晶体与衬底材料晶体之间不可避免地存在晶格失配(可由失配度f= (as-ae) /ae[1]来表示,as、ae分别为衬底和薄膜的晶格常数),外延薄膜晶体中一般都会因失配应变场作用的诱发而形成大量的失配位错,从而严重影响薄膜晶体的使用性能.因此抑制失配位错形成、降低位错密度成为新型晶体薄膜材料发展与产业化的关键.
由于失配应变能只与失配度的平方有关,而与失配度的正负号没有关系,因此,被人们广泛接受的观点是:失配位错的形成、结构以及临界厚度仅与失配度的绝对值大小有关,而与失配度的符号没有关系.最早就失配度符号对位错影响进行研究的是Marée等人[2],他们根据薄膜晶体原子排列与失配应力间的几何关系分析指出:在失配度为正号时,薄膜易形成30°的部分位错;而在失配度为负号时,易形成90°的部分位错.在实验上,这一结果被Wegscheider等人[3]对Si/Ge体系的电镜分析所证实.
随着分子动力学模拟方法的出现和发展,实验上难以实现的对不同失配度符号下位错形成的微观动态过程和机制的研究,成为可能.Ichimura等[4]用分子动力学方法模拟计算测得薄膜的表面台阶形成能会随着失配度符号发生很大变化,甚至由正能量变成负能量.这说明失配度符号对薄膜晶体表面位错形核的确有很大影响.Srolovitz等[5-6]进一步指出:在正失配下,位错的形核是通过许多原子的集体运动从而导致插入一个原子来实现;在负失配下,失配位错是通过挤出一个表面原子而形核.遗憾的是他们的模拟研究都是基于二维分子动力学模型,难以反映薄膜晶体三维原子结构的演变.近年来,开始出现对体心立方晶体中失配位错形成的三维分子动力学模拟[7-8]研究,但未能把正负失配下的位错加以对比研究,以本质地说明失配度符号对位错的影响.本课题组前期模拟研究了负失配时面心立方晶体中位错形成与结构情况[9-10],研究了失配度符号对一维失配外延膜中位错形成与结构的影响[11].
本文以铝膜为研究对象,在保证其它生长条件都一致的情况下,采用三维分子动力学模拟方法进一步考察失配度符号对二维失配外延膜中位错形成与结构的影响.
1 模型与模拟方法运用四阶Predict-Correct算法[12]来求解体系运动方程,时间步长取l0-15 s.采用Ercolessi和Adams[13]建立的嵌入原子法(EAM)多体势来计算铝原子之间的相互作用.该势函数已被应用于铝的表面扩散[14]、层错能与孪晶生长[15]、纳米线[16]分子动力学模拟研究中,得到了与铝的性质和实验数据符合得很好的结果.
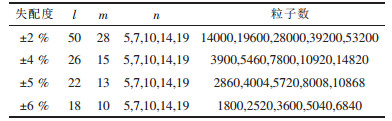
在预置了一定应变的铝衬底上设置同质外延层,拉应变对应正失配度条件下的异质外延生长,压应变则与负失配度的体系对应.这样的体系中,外延晶体和衬底之间只有几何结构上的失配而无化学交互作用,有利于研究失配位错形成的基本规律.外延膜生长面为{111},模拟胞设置如图l所示:在x和y轴方向上运用周期边界条件以模拟无限大的生长面;最底部4层原子在x轴方向即[110]方向预置应变εx、y轴方向即[112]方向预置应变εy,为了研究方便,令εx=εy=ε,并固定其位置作为衬底.这一模拟胞在理论上相当于无穷厚(刚性)的衬底上面积无穷大的外延生长薄膜中的一部分,薄膜在横向没有伸缩余地,与衬底之间在x、y方向有一定的晶格失配,失配度fx=fy=ε.模拟胞的尺寸为:ld110×md112×nd111(l, m, n为各晶向的原子层数,取值如表 1所示,d为面间距).
| 表 1 不同失配度下l, m, n的取值 |
 |
| 点击放大 |
图 1中的恒温区内采用了Gaussian恒温算法(Gaussian热浴)来保持恒温;表面层原子则完全按牛顿力学自由运动,以避免由恒温算法可能引入的失真.观察分析某一时刻体系结构和势能时,要将此时刻体系淬冷到0.001 K以下,以消除原子热运动给体系结构和势能引入的噪声.
 |
| 图 1 外延薄膜模拟胞结构示意图 |
由于研究中所用的模型在二维失配条件下,出现失配位错的时间较短(一般在10 ps内),如果将恒温和加应变驰豫合在一起,无法观察势能曲线和位错出现之间的关系,因此在模拟运算中,将恒温驰豫和加应变驰豫分为两个步骤进行,先恒温驰豫30 ps,待温度稳定后,再加应变,驰豫100 ps.
文中分别对300 K、500 K、700 K和800 K温度下薄膜厚度;分别为1、3、6、10、15个原子层的体系;分别在±2 %、±4 %、±6 %失配度情况进行了模拟研究.
所用的模拟软件和有关工具如下:模拟软件,南昌大学周浪、周耐根等人在Materials Studio、Gaussian 98 03、Molpro等基础上改编、扩展的Molecular Dynamics软件;能量分析,Microcal Origin 6.0;结构分析,Rasmol Version 2.7.0.1和Accelry DS ViewerPro Trial 5.0.
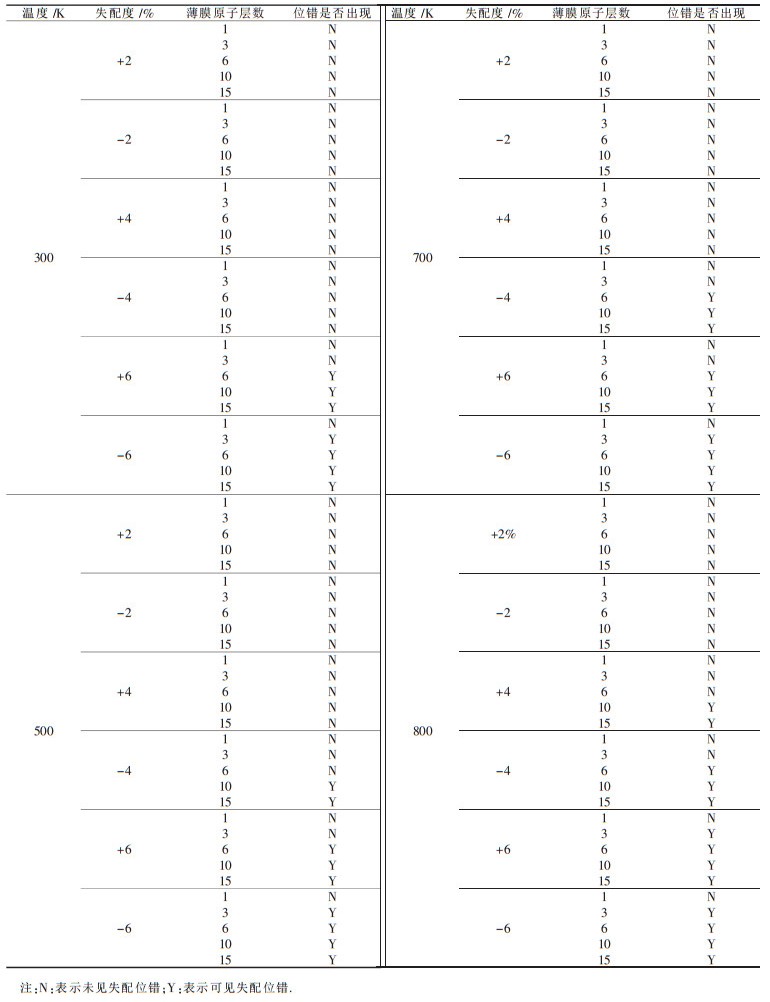
2 结果与讨论 2.1 临界厚度与温度、失配度的关系在对临界厚度与温度、失配度关系的分子动力学模拟研究中,得到如表 2所示的结果.
| 表 2 临界厚度与温度、失配度的关系 |
 |
| 点击放大 |
对表 2的结果进行分析,可获得以下结论:
(1)同一温度下,失配度较小,临界厚度较大,随着失配度的增大,临界厚度减小;
(2)不同温度、同一失配度情况下,临界厚度也有所不同,但温度对临界厚度的影响不是很大;
(3)同一温度、失配度绝对值相同情况下,负失配度的临界厚度要比正失配度的临界厚度更小.
2.2 正负失配度下的体系能量曲线当失配度符号为负号时,外延薄膜的晶格常数大于衬底的晶格常数,要保持薄膜原子和衬底原子的一一对应共格关系,外延薄膜在平行界面的横向上将产生压应变,相应地薄膜在垂直界面的纵向上将产生张应变.当失配度符号为正号时,外延薄膜中的应变状态相反.由于衬底厚度(刚性)比薄膜的厚度大得多,应变集中在薄膜之中,衬底的应变可以忽略.以温度为300 K、薄膜厚度为10个原子层、失配度为±6 %时的体系能量曲线为例,如图 2所示,正失配度时的体系能量大于负失配度时的体系能量.
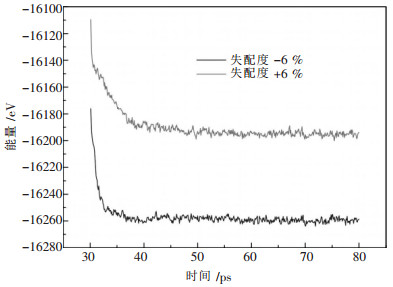 |
| 图 2 失配度分别为+6 %和-6 %时体系的能量曲线 |
由图 2还可知道,失配度符号为负号时的体系总能量下降(释放应变能)时间要早于失配度符号为正号的情况,这说明,在同等条件下,负失配度较正失配度更易产生失配位错.本课题所模拟的其它情况与此类似.
2.3 体系结构图 3和图 4给出了一组失配度为fx=fy=-4 %的外延铝膜在恒温弛豫过程中不同时刻体系延[112]晶向投影和结构图.从图 3和图 4中清楚地再现了外延薄膜晶体中失配位错从形成到增多再到滑移至界面这一过程.在负失配度条件下,位错的形成开始于表层一个倒三角锥形的间隙原子团(图 3(a))引起的局部无序结构,这种无序结构开始是很小的表层结构微扰,进而扩大(图 3(b)),最后失配位错在该结构紊乱区内形成,随着失配位错的形成这种无序结构消失(图 3(c)、图 3(d)的中间部分),类似于“局部熔融重结晶”的过程[10].无序的紊乱或熔融状态为原子运动重组创造了条件.
 |
| 图 3 温度为800 K、薄膜厚度为10个原子层、失配度为-4 %的铝薄膜外延生长过程中不同时刻的体系[112]投影 |
 |
| 图 4 温度为800 K、薄膜厚度为10个原子层、失配度= -4 %的铝薄膜外延生长过程中不同时刻的体系结构图 |
图 5、图 6给出了一组失配度为fx=fy=+4 %的外延铝膜在恒温弛豫过程中不同时刻体系沿[112]晶向投影和结构图.从图 5和图 6中同样清楚地再现了外延生长薄膜晶体中失配位错形成的过程.和失配度为负的时候一样,正失配度时位错也是从薄膜的表面开始形核.不同的是,正失配度时位错的形成开始于表层局部原子的相对滑移带来的一个畸变区.本文做了其滑移细节的动画过程,该畸变区的出现是一个由不清晰到逐渐清晰、由小逐渐变大的过程,在体系的4个角上都将出现这种畸变区,并逐渐运动到薄膜与衬底界面附近,并驻留在离界面2~3个原子层的位置(图 5(d)、图 6(d)).失配位错包含在畸变区内部.结构稳定后,在薄膜表面会出现凹陷.
 |
| 图 5 温度为800 K、薄膜厚度为10个原子层、失配度= + 4 %的铝薄膜外延生长过程中不同时刻的体系[112]投影 |
 |
| 图 6 温度为800 K、薄膜厚度为10个原子层、失配度= + 4 %的铝薄膜外延生长过程中不同时刻的体系结构图 |
3 结论
通过三维分子动力学模拟考察了二维失配情况下失配性质对外延薄膜晶体中失配位错的影响.在失配度符号分别为正号和负号时,外延薄膜分别处于张应力和压应力状态,对应的临界厚度、位错形成时间、形核机制、结构组态都有所不同.
同等条件下:
(1)负失配度的临界厚度比正失配度小;
(2)负失配度情况下的位错形成时间较正失配度短;
(3)负失配度下,位错的形成始于表层一个倒三角锥形的间隙原子团;正失配度下,位错的形成始于表层原子的畸变区;
(4)结构稳定后,负失配度体系在表层挤出局部原子层;正失配度体系会出现凹陷.
| [1] |
吴自勤, 王兵.
薄膜生长[M]. 北京: 科学出版社, 2001: 122.
|
| [2] |
Marée P M J, Barbour J C. Generation of misfit dislocationsin semiconductors[J].
J.App1.Phys., 1987, 62(11): 4413. DOI: 10.1063/1.339078. |
| [3] |
Wegscheider W, Cerva H. Effect of compressive and tensile strain on misfit dislocation injection in SiGe epitaxial layers[J].
J.Vac.Sci.Techno1.B, 1993, 11(3): 1056. DOI: 10.1116/1.587007. |
| [4] |
Ichimura M, Narayan J. Role of surface step on misfit dislocation nucleation and critical thickness in semiconductor heterostructures[J].
Mater.Sci.Eng.B, 1995, 31(3): 299–303. DOI: 10.1016/0921-5107(94)01146-X. |
| [5] |
Smith R W, Srolovitz D J. Void formation during film growth:A molecular dynamics simulation study[J].
J.App1.Phys., 1996, 79: 1448. DOI: 10.1063/1.360983. |
| [6] |
Dong L, Selmitker J, Smith R W, et al. Stress relaxation and misfit dislocation nucleation in the growth of misfitting films:A molecular dynamics simulation study[J].
J.Appl.Phys., 1998, 83(1): 217. DOI: 10.1063/1.366676. |
| [7] |
Liu W C, Huang H C. Dislocation nucleation and propagation during thin film deposition under compression[J].
Computational Materials Science, 2002, 23: 155. DOI: 10.1016/S0927-0256(01)00231-2. |
| [8] |
Liu W C, shi S Q, Woo C H, et al. Dislocation nucleation and propagation during thin film deposition under tension[J].
Computer Modeling in Engineering and Sciences, 2002, 3(2): 213. |
| [9] |
周耐根, 周浪. 外延生长薄膜中失配位错形成条件的分子动力学模拟研究[J].
物理学报, 2005, 54(7): 3278.
DOI: 10.7498/aps.54.3278. |
| [10] |
周耐根, 周浪. 面心立方晶体外延膜沉积生长中失配位错的结构与形成过程[J].
物理学报, 2006, 55(1): 372–376.
DOI: 10.7498/aps.55.372. |
| [11] |
周耐根, 周浪. 失配性质对面心立方外延晶体失配位错结构及其形核机制的影响[J].
人工晶体学报, 2006, 35(1): 74–80.
|
| [12] |
Gear C W.
Numerical initial value problems in ordinary differential equation[M]. Englewood Cliffs, NJ: Prentice-Hall, 1971: 1-54.
|
| [13] |
Ercolessi F, Adams J. Interatomic potentials from 1st-principles calculations-the force-matching method[J].
Europhysics Letters, 1994, 26: 583. DOI: 10.1209/0295-5075/26/8/005. |
| [14] |
Bockstedte M, Liu S J, Huang H C. Diffusion of clusters down(111) aluminum islands[J].
Computational Mutrials Science, 2002, 23(4): 85. |
| [15] |
周耐根, 周浪. < 111>铜膜中孪晶形成与出现几率的分子动力学模拟[J].
金属学报, 2004, 40(9): 897.
|
| [16] |
卢敏, 周耐根, 周浪. 温度对金属纳米线势能分布的影响[J].
原子与分子物理学报, 2007, 24(3): 582.
|
 2011, Vol. 2
2011, Vol. 2

