| 铜冶炼全悬挂转炉扭力杆有限元分析 |
转炉是炼钢厂生产的关键设备之一,同时也是铜、锍、镍等金属火法生产流程中熔炼、吹炼和精炼等阶段的重要设备[1-2],其倾动装置用于炉体的平稳启动及准确定位,扭力杆是大型转炉倾动机构的缓冲装置,具有平衡减速箱壳旋转力矩和缓冲传动系统冲击的作用.目前大部分扭力杆缓冲装置在使用初期设计许用应力不足,致使扭力杆发生断裂、弯曲[3-5].扭力杆失效属于高应力、低周次、多源的疲劳断裂[6].通过参数化分析结果的研究,可以获得一个多个参数变化对扭力杆的影响,获得最危险的工况以及最优化的扭力杆仿真模型[7-8].在转炉制动过程中,炉体与减速箱保持相对静止绕耳轴旋转,减速机下方左右两根立杆承受大小相等方向相反的拉力、压力,并传递给扭力杆使其发生扭转,起到缓冲作用[9].为全面了解扭力杆变形及应力分布状态,采用Ansys Workbench确定其扭转位移、强度、刚度,为进行扭力杆有限元分析提供可靠的数据来源.
1 扭力杆力学模型倾动机构是由一次、二次减速机与扭力杆缓冲装置组成,其作用是倾动炉体,完成兑铁水、加废钢、取样、出钢和倒渣一系列操作,可使炉体正反转360°,并使炉体安全、准确地停在要求的位置上,如图 1所示.扭力杆位于减速机下方,其左右两端安装在轴承座上,在炉体制动过程中,扭力杆起到支撑和缓冲的作用是倾动机构重要的零部件,扭力杆三维示意图如图 2.
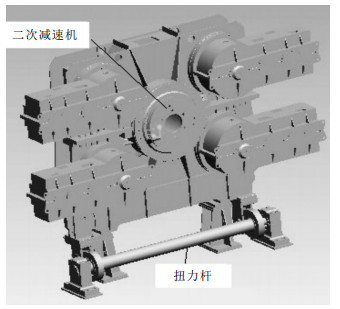 |
| 图 1 转炉倾动及缓冲系统的仿真示意图 |
 |
| 图 2 扭力杆三维示意图 |
扭力杆从结构上看是左右两端对称,中部半径R1 =110 mm,锥形段平均半径R2 =247.5 mm,推杆作用面半径R3 =300 mm,曲柄偏心距S =700 mm.对于全悬挂推杆作用力:
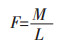
|
(1) |
式(1)中M为耳轴扭矩,L为两垂直杆中心线的距离,某钢厂转炉耳轴最大倾动力矩为1000 kN·m,两垂直杆中心线距离为3300 mm.
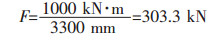
|
确定扭力杆两端扭矩:
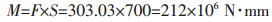
|
由扭力杆结构的对称性,为节省计算时间,提高计算效率,故取扭力杆的一半为研究对象,采用Mechanical中进行三维实体分析默认的SOLID186单元以及材料为结构钢作为基本单元进行分析,设置relevance为fine,扭力杆有限元单元网格划分如图 3所示.计算参数:节点数为22990,单元数为12945.
 |
| 图 3 扭力杆有限元单元网格划分 |
2.2 边界约束条件的确定
由于扭力杆为对称结构,在反对称扭矩M的作用下,扭力杆中部对称面为零位移截面,故约束扭力杆中心对称截面位移自由度,作为扭力杆边界约束条件[10].将扭矩平均分配到两个推杆上,将106×106 N ·mm以边载荷作用方式施加到扭力杆相应边上.其位移边界约束及扫矩载荷分别见图 4、图 5.
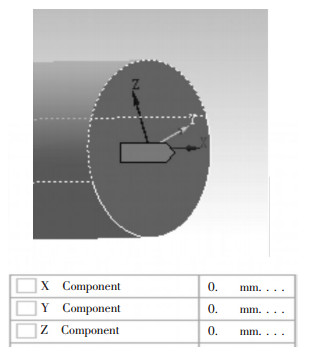 |
| 图 4 位移边界约束 |
 |
| 图 5 扭矩载荷 |
3 计算结果及分析 3.1 位移
假定以扭力杆对称中心为原点,建立以半径R、转动线位移T和扭力杆轴线为坐标轴的柱坐标系.在正常工况下,在扭力杆两端连接板面作用的扭矩106×106 N·mm下,扭力杆会产生一定的线位移,如图 6所示,此时红色区域最大位移为1.2668 mm,发生在扭力杆连接杆作用面上,而扭力杆轴心处位移各点都为0 mm,其值与左侧标尺相对应.
 |
| 图 6 扭力杆扭转综合位移分布云图 |
3.2 应力
从扭力杆的应力分布状态来看,扭力杆可看成等值圆轴纯扭转,剪应力是扭力杆横截面上主要分量,扭力杆中的最大剪应力对其强度刚度的影响有很大作用.为全面了解扭力杆强度刚度的情况,本文将从最大等效应力(Equivalent Stress)和最大主应力(Maximum Principal Stress)两个方面进行分析.
(1)最大等效应力(Equivalent Stress).等效压力分布见图 7.
 |
| 图 7 等效应力分布图 |
从图 7可以看出颜色不同分布代表其应力分布红色和黄色受到的等效应力最大,其最大等效应力为97.173 MPa,由于扭力杆两端固定在轴承座上, 故不受扭矩影响其值基本为0 MPa.
(2)主应力(Maximum Principal Stress).最大主应力分布见图 8.
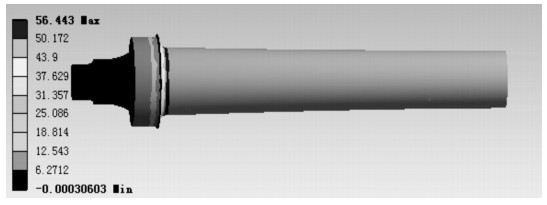 |
| 图 8 最大主应力分布图 |
对于纯扭转剪应力的作用不可忽视,它是扭力杆横截面上应力的主要分量,无论是复杂应力状态还是简单应力状态,剪应力都是影响扭力破坏的主要因素.从图 8可以知道最大主应力为56.443 MPa,黄色部位应力为50.172 MPa,危险截面均生在半径为110 mm的扭力杆外表面上.
由材料力学可知,圆轴扭转可视为纯剪切应力状态,在此状态下,半径为110 mm外表面受到的最大主应力为: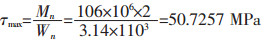
通过对转炉缓冲装置扭力杆在转炉最大倾动力矩的情况下,对其进行有限元分析可以得到以下几点结论:
(1)本文利用Pro/E对扭力杆进行三维实体建模与Ansys Workbench联合进行扭力杆静力学有限元分析.
(2)在扭力杆工作过程中,其中部是危险部位,其破坏形式将可能从中部发生断裂破坏.
(3)扭力杆最大切向线位移为1.2668 mm,其发生部位在扭力杆两端连接杆作用面上,而两端轴心处基本不受扭矩影响;
(4)扭力杆中部区域可视为纯剪切应力状态,最大应力值为56.443 MPa.
| [1] | 宋海鹰. PS转炉铜梳吹炼过程建模与优化控制方法的研究及应用[D]. 长沙: 中南大学博士论文, 2008. |
| [2] | 任鸿九, 王立川. 有色金属提取冶金手册·铜镍[M]. 北京: 冶金工业出版社, 2000. |
| [3] | 陈胜, 陈克非, 瞿东利. 新型转炉倾动液压缓冲装置的应用[J]. 冶金设备管理与维修, 2010, 28(2): 14–15. |
| [4] | 童靳于, 潘紫微, 包家汉, 等. 转炉扭力杆缓冲装置三维非线性有限元分析[J]. 冶金设备, 2010(4): 34–37. |
| [5] | 王欠欠, 魏江. 转炉倾动机构中扭力杆的校核[J]. 重工与起重技术, 2009, 23(3): 18–19. |
| [6] | 陆频. 扭力杆的断裂分析[J]. 热处理, 2003, 2(18): 29. |
| [7] | Nikravesh PE. Computer-aided Analysis of Mmechanical Systems[M]. Englewood Cliffs: Printice-Hall, 1998: 10-20. |
| [8] |
Mahmood M.shokrieh, Davood Rezaei. Analysis and Optimization of a Composite Leaf Spring[J].
Composite Structure, 2003, 60: 317–325. DOI: 10.1016/S0263-8223(02)00349-5. |
| [9] | 张玉忠. 转炉倾动机构扭力杆的有限元分析[J]. 机械管理开发, 2006, 90(3): 33–35. |
| [10] | 高素荷. 大型转炉倾动机构扭力杆有限元分析[J]. 计算机辅助工程, 2006, 15(9): 312–313. |
 2011, Vol. 2
2011, Vol. 2

