| 基于非线性回归的矿产品价格预测研究 |
2. 浒坑钨矿,江西 安福 343205
2. Huken Tungsten Mine, Anfu 343205, China
矿山工程投资项目所创造的经济效益是工程项目投资所追求的最主要目的之一,是评价一个项目是否可行、是否具有盈利性、是否具有偿还债务能力的前提,对项目经济效益的评价结果是投资决策的直接依据[1-3].矿山工程投资项目的经济效益在表现形式上可分为直接效益和间接效益,有形效益和无形效益,正效益和负效益.不同效益的经济评价就必须采用不同的视角或是不同的经济理论方法来实现[4].矿山工程投资项目经济评价的宗旨就是要对项目投资给矿山所带来的效益进行定量的财务以及定性的国民经济和社会评价,根据对效益分类的了解,财务经济评价主要是针对有形效益、直接效益;国民经济及社会评价的对象基本是无形或间接效益.
矿山工程投资项目的财务经济评价主要是基于可行性研究和评价,是对将来工程建设及投产后情况的预测,包括矿产储量预测,矿产品市场分析、价格预测等,其中矿产品价格预测一方面为确定矿山项目建设规模和提供依据,另一方面为矿山项目建成后的市场营销打下基础[5].因此,要解决矿山项目投入的可得性和可靠性问题,必须对矿产品的价格进行预测.
1 矿产品价格预测模型的建立根据市场近年矿产品历史价格运用一元曲线拟合回归数学方法建立相关模型对未来几年矿产品市场价格进行预测.长远来看,矿产品价格在不断地上下波动,受市场供求关系的影响,价格起伏不定,所以不能利用一元线性回归模型来预测以后几年矿产品的市场价格,通过统计近年来矿产品市场价格,针对数据变化的规律,建立一元非线性拟合回归模型来预测未来几年内矿产品的价格,并利用模型的算法来实现价格预测.
非线性拟合模型的建立
(1)拟合原理.对于给定一组数据{(xi, yi), i=1, 2, …, N}, 若希望采用多项式模型对该数据组进行描述,且拟合的目标是对于形如y(x)=f(a, x)= a1xn+a2xn-1+…+anx+an+1的n阶多项式模型,求取参数a1, a2, …, an, an+1使下列x2量最小[6].
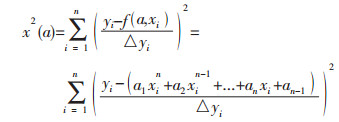
|
(1) |
在△yi=△y不变的假设下,使式(1)达到最小的解是:
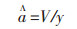
|
(2) |
(2)拟合阶数的确定.拟合的目标是形如y(x)= f(a, x)=a1xn+a2xn-1+...+anx+an+1)的n阶多项式,多项式的阶次取得太低,拟合就粗糙;阶次太高,拟合“过头”,使数据噪声也被纳入模型.判断拟合的阶次是否恰当的方法很多,在此介绍3种方法[7-8].①如果估计参数下的x2量与其自由度相近,认为阶次适当,把所得参数估计代入式(1)计算x2量,一个合适的阶次应该使x2量以自由度(N-n-1)为期望值.这里N是原数据的长度,(n +1)是多项式系数的数目;②如果Q(x2,N-(n+1))=1-P(x2 < (N-n-1))与0.5接近,认为阶次适当,认为阶次适当.P(x2 < (N-n-1))利用x2分布的累积概率指令chi2cdf(chi2, (N-n-1))算出;③利用传统的方法,根据已知的数据绘制出以x为横坐标,以y为纵坐标的散点图,每一对数据(xi, yi)作为一个点在坐标纸上标出来(i=1, 2, …, n),将计算得到的模型a1, a2, …, an, an+1值代入模型中,模型的阶数从小依次取值1,2,3,4,5(为保证计算精度,拟合多项式的阶数一般不超过5阶),将得到的模型曲线也绘制到图纸上,从散点图和曲线图的对比来确定拟合达到最佳效果的曲线的阶数,
由于上述第3种方法的直观性与方便性,本次模型建立首先利用近年来矿产品价格变化散点图,并利用相关程序得到模型参数并绘制拟合后的模型曲线图,与散点图对比以确定模型的最佳拟合阶数.
2 应用实例为验证矿产品价格预测模型,以氧化钼为例,建立钼矿产品价格预测模型,并利用该模型进行未来几年钼矿产品的价格预测.近年来,世界钼的生产格局没有发生大的变化,美国、智利和中国仍是世界上产钼最多的国家,这三个国家的钼产量占世界钼总产量的75 %以上.1991年世界钼的产量为11.5万t,2004年的钼产量为13.9万t,年均增长率1.47 %.产量增长较为缓慢,主要的原因是1995年以后,国际矿产品市场金属价格全面下降,从1996-2002市场上的钼价长期低迷状态.同时期国际铜价也处于低迷状态,导致1999-2002年世界上大规模关闭高成本矿山或压减铜矿山的产量,其结果也限制了钼的产量.另外,2004年中国钼矿大量减产,钼精矿产量约6.3961万t,比上年同期减少8.66 %,进一步加剧了供需矛盾.因供需失衡,导致价格上涨.
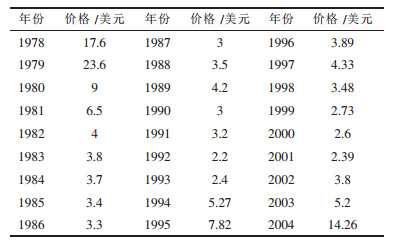
综观国际市场钼价,其变化很大.表 1是近30年美国历史上氧化钼价格.
| 表1 美国市场近30年氧化钼价格 |
 |
| 点击放大 |
首先根据近30年来氧化钼国际市场价格绘制了价格-时间散点图,然后依次假设模型多项式的阶数为1-6,利用MATLAB的曲线拟合命令得到模型的相关系数a1, a2, …,an, an+1,绘制得到相关拟合曲线图(如图 1),与价格-时间散点图对照得到最佳拟合曲线,并由此曲线确定模型的多项式系数与阶数.
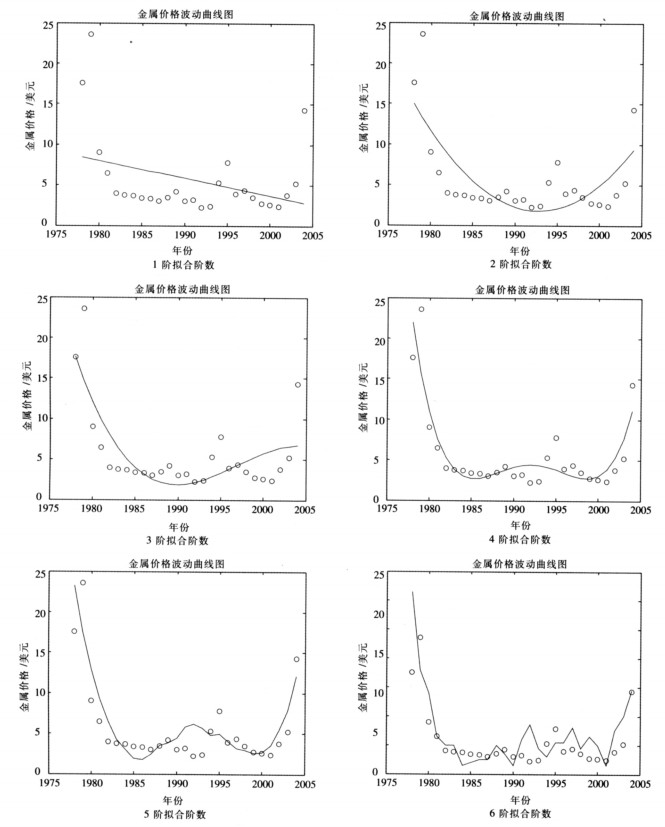 |
| 图 1 不同阶数多项式拟合曲线图 |
由图 1可以看出,拟合后的曲线只有拟合阶数为4的曲线图与原散点图吻合较好,说明该模型多项式最佳拟合阶数为4阶,将该拟合阶数代入程序,得到4阶拟合后模型的相关系数a1,a2,a3,a4,程序计算结果如下:
a1= 8.4247e-004,a2 = -6.7128,a3 = 2.0058e+004,a4=-2.6636e+007,a5=1.3265e+010
最终拟合的模型方程为:y (x)=(8.427e-004)x4-6.7128x3+(2.0058e+004)x2+(-2.6636e+007)x+13.625
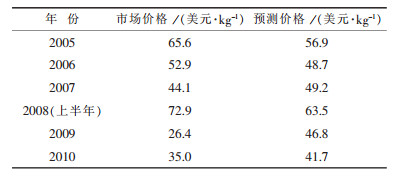
根据上述建立的拟合方程,将2005-2010年代入该模型得到最终预测价格.表 2是预测价格与市场实际价格,相比对发现2005 ~2007,该模型预测价格具有一定的代表性,2008年上半年,国际钼需求量大幅增加,致使预测价格与实际价格略有差距,从2008年下半年开始,世界经济大幅衰退,全球钢铁行业大幅度减产,市场的钼需求量萎缩,致使2008年底钼价跌至20.93美元/kg,世界金融危机属于特例,致使2008~2009年预测价格与实际价格差距较大.2010年,世界经济回暖,国际钼价开始上扬,计算发现,预测价格与实际价格相差幅度开始减小.总的比较发现,只要世界经济平稳发展,价格波动在合理范围之内,该模型预测价格与市场价格较为接近,该预测模型具有一定的实用性.
| 表2 预测价格与实际价格比较 |
 |
| 点击放大 |
3 结论
本文以矿山项目投资决策为背景,利用非线性预测方法建立了矿产品价格预测模型,并在分析氧化钼矿产品历史价格的基础上,对价格曲线图进行拟合,得出适合矿产品价格走向的曲线的拟合方程来对氧化钼矿产品未来的价格进行预测.实践证明,该模型具有一定的代表意义,在一定程度上能利用该模型对矿产品未来价格做出预测.
| [1] | 孔晓青. 改扩建项目技术经济评价方法探讨[J]. 冶金经济与管理, 2001(4): 17–19. |
| [2] | 秦德先, 刘春学. 矿产资源经济学[M]. 北京: 科学出版社, 2002. |
| [3] | G.戴维斯. 矿产品价格预测在矿物工程评估中的应用[J]. 国外金属矿山, 1997(3): 14–19. |
| [4] | 李定荣, 李开孟. 建设项目可行性研究[M]. 天津: 天津大学出版社, 1994. |
| [5] | Porter M.E. Competitive Advantage: Creating and Sustaining Superior Performance [M].New York, 1985. |
| [6] | 邓聚龙. 灰色预测与决策[M]. 武汉: 华中理工出版社, 1980. |
| [7] | 陈章潮, 熊岗. 应用灰色系统原理进行长期电力需求预测[J]. 系统工程, 1994, 12(2): 67–69. |
| [8] | 张树京, 齐立心. 时间序列分析简明教程[M]. 北京: 清华大学出版社, 2003. |
 2011, Vol. 2
2011, Vol. 2

