有色金属科学与工程  2011, Vol. 2 Issue (1): 96-100
文章快速检索     高级检索
引用本文
0
赵运才, 任继华, 左亮涛. 基于MATLAB的齿轮参数优化设计[J]. 有色金属科学与工程, 2011, 2(1): 96-100.
ZHAO Yun-cai, REN Ji-hua, ZUO Liang-tao. The Gear Parameter Optimization Design Based on the Matlab[J]. Nonferrous Metals Science and Engineering, 2011, 2(1): 96-100.
基于MATLAB的齿轮参数优化设计[PDF全文]
赵运才 , 任继华 , 左亮涛     
江西理工大学机电工程学院，江西 赣州 341000
作者简介：赵运才（1964-），男，博士，教授
收稿日期：2010-12-01
摘要：对二级齿轮建立优化设计数学模型，运用MATLAB软件中的优化工具箱对其进行计算，得到优化后的齿轮参数，通过试验证明，优化后的齿轮参数降低了产品生产成本、减小了齿轮重量，是一种行之有效的方法.
关键词：齿轮    MATLAB    优化设计    
The Gear Parameter Optimization Design Based on the Matlab
ZHAO Yun-cai, REN Ji-hua, ZUO Liang-tao    
Faculty of Mechanical and Electronic Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
Abstract: This paper studies the mathematical model of optimum design for the double gear by calculating the optimal toolbox of Matlab software. The optimized parameters are obtained. Experiments show that the optimized gear parameter reduces production cost and gear weight.
Key words: gear    Matlab    optimization design    
0 优化设计的必要性

在优化之前，采用传统的设计方法，将它设计成第一级为金属蜗杆与塑料斜齿轮啮合，第二级为粉末冶金小齿轮与塑料输出齿轮啮合.第二级小齿轮采用粉末冶金材料，提高小齿轮的抗疲劳强度，因为在传统设计中，小齿轮设计采用正变位，以及采用粉末冶金材料，目的是提高其抗疲劳强度(小齿轮的啮合次数高于相啮合的大齿轮)[1].但这个设计仍然存在缺点，小齿轮采用大的正变位，必然造成小齿轮的齿顶变尖，齿顶圆倒角很小，如果与塑料齿轮啮合时，必然造成塑料齿轮的面刮伤，很多次循环运转后，塑料齿轮疲劳磨损严重，当磨损到一定范围时，塑料齿轮齿厚变薄，强度降低，直至塑料齿轮断裂.失效齿如图 1.

图 1 失效齿轮

1 二级减速器参数优化的数学模型 1.1 设计要求

电机的空载转速为4600~5000 r/min，堵转扭距为0.28~0.32N·m.

电机经过减速器后，它的速度要求是22 r/min，输出堵转扭距是22N·m.

从减速器输出的性能曲线可知：输出速度为26~ 28 r/min，堵转扭矩为22~25 N·m.

按以上参数计算出的传动比为

最大传动比是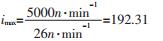

最小传动比是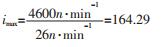

1.2 设计变量的选择

设计变量是相互独立的基本参数，由设计人员直接控制，它影响设计属性的变化[2].对于减速器箱体，设计变量为传动比i、齿轮齿数Z、斜齿轮模数m、蜗轮蜗杆模数m、齿宽B、螺旋角β、用设计变量表示为

 1.3 目标函数的推导

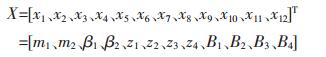
各齿轮几何尺寸越小，一方面可以节省材料和减少齿轮加工费用；另一方面齿轮的重量越小，则齿轮的转动惯量和运动的圆周速度越小，因此转动轴上受到的动载波动量越小，齿轮传动也越平稳，最终传给齿轮箱的振动也越小[3].

以所有齿轮的质量之和最小作为目标函数，因为材料密度一定，可以转化为所有齿轮体积之和最小.

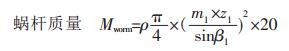
(1)
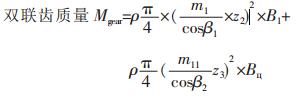
(2)
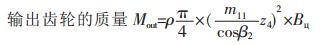
(3)
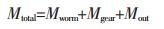
(4)

铁的密度是7.8g/cm3, 塑料的密度是1.4g/cm3.由式(1)~式(4)可以看出，齿轮的质量之和Mtotal仅由齿宽BⅠ、BⅡ齿轮齿数Z1、Z2、Z3、Z4，模数mⅠ、mⅡ, 以及螺旋角β1、β2所决定.即为这些参数的函数.

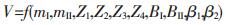
若取它们为设计变量并表达为

则目标函数可以写成：

 1.4 约束条件的确定

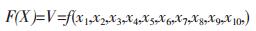
(1) 确定变量的上下限.蜗轮蜗杆的螺旋角, 考虑蜗杆必须自锁以及传动效率不能太低[4]，蜗轮蜗杆螺旋角

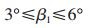
圆柱齿轮副的螺旋角, 尽量提高重合度，提高齿的承受能力，但又不能有太大的轴向力，造成端部摩擦太大，以及角度太大, 造成塑料齿轮脱模难度.

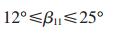
为了自锁，蜗杆头数一般不宜超过2头.

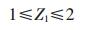
根据给定总传动比164.29~192.31, 输出的最大扭矩为25N·m最大[5].

蜗轮齿数1≤Z2≤60；双联齿轮小齿轮齿数7≤Z3≤12；输出齿轮齿数30≤Z4≤40；蜗杆副模数0.7≤m1≤1.0；圆柱齿轮副1.2≤m11≤1.5.

由齿轮的强度计算公式可知，齿轮愈宽，承载能力愈高，因而齿轮不宜过窄；但增大齿宽又会使齿面上的载荷更趋不均匀，故齿宽系数应取得适当.当两支承相对小齿轮作不对称布置时，齿宽系数ϕd取0.7~1.15[6].

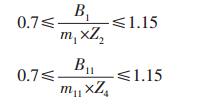
(2) 根据齿轮设计手册计算齿轮的接触强度和齿轮弯曲强度的约束.齿轮的接触强度应小于其许用值.

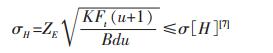
对于塑料材料工作在60°时弹性影响系数为

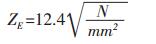
齿轮强度载荷系数K=KAKVKαKβ

根据工况，选取KA=1.35 KV=1.5 Kα =1.2[8]

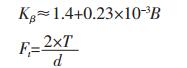
经查表直POM的许用接触应力为18MPa, PA66许用接触应力为25MPa.将其代入公式得:

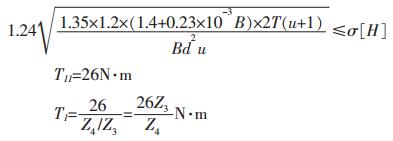
(3) 齿轮的弯曲强度疲劳应小于许用值.

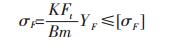
K为载荷修正系数

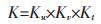
根据齿轮手册的图表[9]可以查得.

POM的弯曲疲劳强度是38MPa, PA66的弯曲强度是55MPa.

 1.5 建立优化数学模型

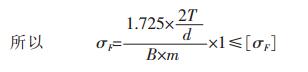
建立优化数学模型如下：

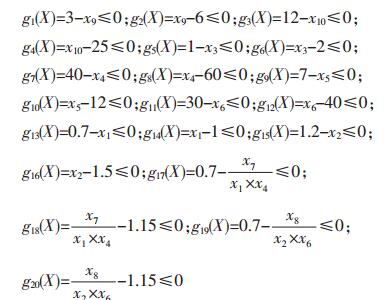
接触应力约束函数为：

弯曲强度约束函数为：

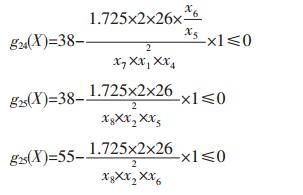
这是一个有10个设计变量，25个不等式约束条件的非性线优化设计问题，基于对优化算法的讨论，可采用惩罚函数内点法计算，MATLAB软件优化工具箱可以直接调用函数进行计算[10].

1.6 优化结果及结论

(1) 计算结果.设计变量为：

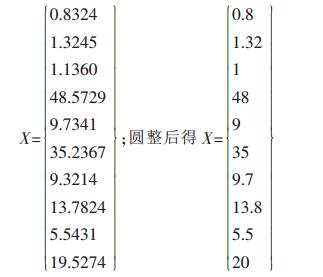
目标质量优化结果M=66.5577g.

(2) 优化设计前后参数对比.原始设计方案与优化后设计比较如表 1所示.

表 1 优化设计前后参数对照表
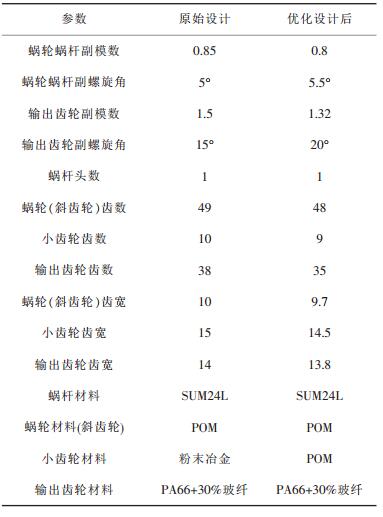点击放大

(3) 设计前后重量对比.原始设计齿轮实物如图 2所示，优化设计后齿轮实物如图 3所示.

图 2 原始设计齿轮实物图

图 3 优化设计后齿轮实物图

原始设计，齿轮组件和齿轮箱(塑料)实物及其重量为133g，如图 4所示，优化设计后，齿轮组件和齿轮箱(塑料)实物及其重量为111g，如图 5所示.

图 4 原始设计齿轮组件实物重量

图 5 优化设计后齿轮组件重量

2 结束语

上述研究表明，优化后，齿轮箱重量由原来的133g减少到111g，重量减少16.54%, 成本降低约40%, 小齿轮材料由粉末冶金改为POM, 材料成本降低, 从加工工艺方面, 原来要将粉末冶金材料压模在塑料成型，优化后可以直接成型.

利用MATLAB优化工具箱对斜齿轮传动进行多目标设计，达到了设计的预期目的[11].

参考文献
[1]
杜平安, 梁锡昌. 齿轮传动的现代设计方法[M]. 北京: 机械工业出版社, 1994.
[2]
王科社. 机械优化设计[M]. 北京: 国防工业出版社, 2007.
[3]
刘鹤松, 崔胜明. 基于MATLAB的汽车变速器优化设计方法[J]. 哈尔滨工业大学学报, 2004, 36(1): 112–114.
[4]
胡少刚, 姜雷. 基于MATLAB的蜗轮蜗杆减速传动的优化设计[J]. 常州工学院学报, 2010, 23(1): 16–19.
[5]
苗君明, 佟刚. 基于MATLAB的齿轮减速优化设计[J]. 沈阳航空工业学院学报, 2005, 22(5): 33–34.
[6]
蒋春明, 阮米庆. 基于MATLAB的斜齿轮多目标优化设计[J]. 传动技术, 2006, 20(4): 7–9.
[7]
谢剑刚, 陆维良. 齿轮减速机啮合优化参数设计[J]. 煤矿机械, 2003(6): 30–32.
[8]
陈满意. 基于MATLAB的齿轮减速器的可靠性优化设计[J]. 机械传动, 2002(3): 34–36.
[9]
许洪基. 齿轮手册(上, 下册)[M]. 北京: 机械工业出版社, 1995.
[10]
宋敏, 王巧云. 圆柱齿轮减速器优化设计[J]. 西安航空技术高等专科学校学报, 2001(3): 3–6.
[11]
赵又红, 符炜, 罗显光, 等. 二级圆柱齿轮减速器的多目标优化设计[J]. 湘潭大学自然科学学报, 2003, 25(2): 81–84.