| 铁液中Al2O3纳米颗粒溶解和熔化的热力学研究 |
b. 江西理工大学, 理学院, 江西 赣州 341000
b. Faculty of Science, Jiangxi University of Science and Technology, Ganzhou 341000, China
近年来, 利用钢中的细小第二相粒子(夹杂物[1]或/析出物[2]或/外加的微小粒子[3-4])作为非均质形核质点, 弥散细化非金属夹杂物以及促进晶内铁素体形核细化组织的“微小颗粒冶金”研究受到重视, 对提高钢的性能起到很大作用.但目前人们对微小颗粒在钢铁熔体中的基本热力学问题研究很少, 仍采用块体材料的性质代替微小颗粒的性质来进行研究, 影响结果的准确性.鉴于洁净钢冶金技术的快速发展趋势, 准确理解纳米级超细颗粒在钢铁熔体中的特殊行为显得十分必要.通常, 钢中的Al2O3夹杂物属于块体材料尺度范畴, 严重影响钢材的力学性能, 其熔点高, 在钢液中呈固态形式存在.当Al2O3尺寸细化至纳米级后, 不仅可减轻其危害作用, 而且对提高钢的综合力学性能起到有利作用, 如超细粒子作为基体的形核核心(凝固或固态相变)或者钉扎晶界阻碍晶粒长大(固态相变), 从而达到细化基体组织而获得的强韧化作用等[4-5].与块体尺度的Al2O3相比, 纳米Al2O3的溶解度增加, 影响其在钢液中的溶解反应平衡, 进而影响钢液的[O]含量, 也即影响钢的洁净度; 另外, 纳米Al2O3熔化温度(熔点)降低, 那么在钢液温度下是否仍能保持固态形式(关系到其能否作为新相非均质形核核心), 这些都是必须探讨的问题.笔者在分析铁液中Al2O3纳米颗粒溶解和熔化过程的基础上, 对纳米Al2O3在铁液中的溶解反应平衡常数(元素平衡溶度积)和熔化温度(熔点)进行了推导和计算, 获得了对Al2O3纳米颗粒在铁液中溶解和熔化过程的基本认识, 为进一步研究钢铁熔体中纳米尺度颗粒的行为以及高洁净钢冶金的理论问题提供一些基础.
1 纳米Al2O3在铁液中的溶解平衡热力学宏观系统的热力学研究已非常完善, 但不适合于描述纳米尺度体系的热力学性质.在宏观热力学平衡体系中, 不考虑外场影响时, 内能可表示为U=TS-PV+μN.对于纳米尺度体系, T. L. Hill引入一个被称为“subdivison energy”的新物理量W来反映材料尺寸对热力学的影响, 提出纳米尺度体系的内能表达式为Unano=(TS-PV+μN)+W[6-7], 吉布斯自由能可表示为ΔGnano=ΔH–T(ΔS)+[Σ(μ·dn)]+(E·dN), 式中E·dN相当于纳米尺度体系带来的额外能量变化, E为体系中类似于化学势μ的能量, 在此可称为纳米势(nanopotential), N为体系中纳米颗粒的数量, E·dN与纳米颗粒的尺寸有关.对于一个化学反应过程, 如果有纳米尺度的颗粒参加, 则反应过程的能量变化不同于常规体系, 必然会对化学反应的平衡程度(限度)产生影响.下面以纳米Al2O3在铁液中的溶解为例予以探讨.
假设有以下两个反应, 反应式(1)和式(2)分别表示常规尺度和纳米尺度的Al2O3颗粒的溶解反应:
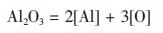
|
(1) |
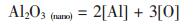
|
(2) |
对于反应(1), Gibbs变化可根据常规热力学数据计算, ΔG(1)=ΔH–T(ΔS)+Σ(μ·dn), 进而可求解反应的平衡常数K(1).对于反应(2), 为纳米颗粒的溶解平衡, 由于溶解过程反应物的界面能高, 即E·dN较大, 与常规的Gibbs变化相比, E·dN不可忽略, 其溶解反应总的Gibbs变化应为ΔG(2)=ΔG(1)+E·dN.所以, 反应(1)和式(2)的平衡常数可分别表示为:
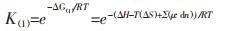
|
(3) |
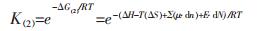
|
(4) |
设常规颗粒和纳米的Al2O3均以纯物质为标准态, 则其活度为1, 反应(1)和反应(2)的溶解元素平衡溶度积可表示为:G(1)
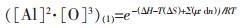
|
(5) |
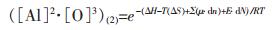
|
(6) |
将式(6)除以式(5), 可得:
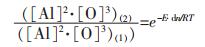
|
(7) |
从式(5)、式(6)和式(7)可以看出, 要计算纳米Al2O3在铁液中的溶解热力学平衡关系, 需首先确定E·dN的数据.由于纳米颗粒的不稳定性, 实验测量工作很难, 目前没有任何这方面的实验测量数据.从大量关于纳米热力学的研究来看, 确定纳米体系的热力学性质比较理想的方法是采用分子动力学进行模拟.本文采用近似处理的界面能方法对纳米Al2O3的溶解平衡进行计算.由于纳米材料尺寸小, 导致界面能显著增加, 增加量可用式(8)来近似处理:
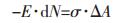
|
(8) |
式(8)中σ为Al2O3与铁液间的界面张力; 为纳米Al2O3相对其常规颗粒的比表面积增量.将式(8)代入式(7):
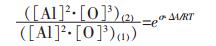
|
(9) |
假设铁液中Al2O3的质量分数为0.01%(基于一般钢液中夹杂物含量为0.01%左右而假定的, 当然质量分数也对溶解平衡有影响, 在此不进行探讨), 形状为球形, Al2O3实密度为4.0×103kg/m3; 其中, Al2O3纳米颗粒的半径为10nm, 常规颗粒Al2O3的半径为10μm.则1kg铁液中所含纳米颗粒Al2O3的数量N为5.97×1015, 比表面积为7.5m2; 所含常规颗粒Al2O3的数量N为5.97×106, 比表面积为7.5×10-3m2.所以, Al2O3纳米颗粒比常规颗粒Al2O3的比表面积的增加量ΔA近似等于7.5m2.理论上讲, σ实际上受颗粒尺寸影响, 这一问题目前还无研究定论, 在此, 以常规颗粒Al2O3与铁液间的界面张力近似替代, 取为2.30J/m2, 可得σ·ΔA=17.25J.将该值代入式(9)中, 可得铁液温度为1873K时(基于一般钢液温度约为1873K左右而假定的, 当然铁液温度也对溶解平衡有影响, 在此不进行探讨), 纳米Al2O3与常规颗粒Al2O3平衡溶度积之比:
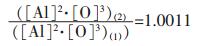
|
(10) |
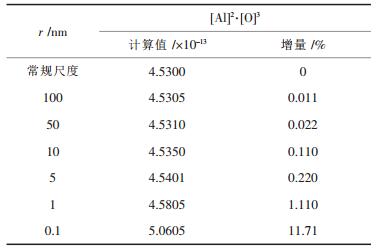
铁液中常规颗粒Al2O3的平衡溶度积[8]为[Al]2· [O]3=4.53×10-13, 所以, 可得温度为1873K的铁液中, 质量分数为0.01%、半径为10nm的Al2O3颗粒的平衡溶度积为[Al]2·[O]3=4.535×10-13.同理, 可计算出0.01%质量分数、半径为1nm的Al2O3颗粒的平衡溶度积为[Al]2·[O]3=4.5805×10-13, 此时平衡溶度积与常规颗粒Al2O3的平衡溶度积之比为1.011.表 1列出了1873K的铁液中, 质量分数为0.01%、不同粒径的Al2O3的平衡溶度积计算结果.从表 1可以看出:随着Al2O3纳米颗粒粒径的减小, 其溶解元素的平衡溶度积不断提高; 而且粒径越小, 平衡溶度积提高的幅度越大.
| 表 1 不同粒径Al2O3在铁液中的平衡溶度积(mass% = 0.01, T = 1873K) |
 |
| 点击放大 |
2 纳米Al2O3在铁液中的熔化 2.1 纳米材料熔化过程分析
材料的熔化过程即为液体(熔体)的非均匀形核过程, 形核起始于材料的表面或亚晶界处, 因为表界面处原子自由能较高, 有利于作为熔体非均匀形核的场所.因此, 材料的熔化过程在很大程度上取决于单位体积中的外表面和内界面面积总和(比表面积), 比表面积愈大, 非均匀形核位置愈多, 熔化温度就愈低.纳米材料存在大量表面或内界面, 其比表面积较常规颗粒材料大很多, 对熔化过程产生重要影响, 使其熔化温度降低.
对于纳米颗粒, 研究得到熔化温度与结合能之间存在T=CE[9]关系, 式T中为纳米颗粒的熔化温度, E为原子结合能, C为常数.从该式可以看出, 纳米颗粒熔化温度下降的物理本质是材料尺寸减小导致比表面积增大, 表面原子数增多, 材料热稳定性下降, 原子结合能减小, 熔化时需要吸收的热量减小.当材料的尺度下降至纳米级(≤100nm)甚至更小时, 其热稳定性在某一临界尺寸时将发生突变性下降.当然, 不同种类的材料, 热稳定性发生突变性下降的程度不同, 所以熔化温度发生突变时的临界尺寸也不同.实验表明, 大块Pb熔化温度为600K, 20nm的Pb微粒熔化温度降低288K[10]; 大块Au熔化温度为1336K, 5nm的Au微粒熔化温度急剧下降至1100K[11].
纳米结构材料是由纳米颗粒通过一定制备方式组合而成的, 所以其熔化温度实际为纳米颗粒的熔化温度, 但其熔化过程不同于纳米颗粒, 可用图 1示意其熔化过程.图 1中, 假设纳米结构材料由A、B两种纳米粒子构成, A和B粒子的半径分别为r1和r2, 熔化温度分别为T1和T2, 对应的相同物质的常规块体材料A和B的熔点分别为TA和TB.如图, 对于半径为r1的粒子A, 当吸热后粒子温度达到熔化平衡温度T1时, 粒子发生熔化, 随后粒子不断吸热, 温度恒定在T1.由于纳米尺度实际是材料的亚稳态尺度, 所以由纳米颗粒组成的纳米结构材料在平衡温度T1时, 彼此相邻的纳米颗粒的晶界要发生迁移、合并及长大(若单个纳米颗粒内部存在亚晶界, 则亚晶界也要发生合并长大), 即发生纳米尺度向常规块体尺度的转变过程.例如, 当纳米粒子A经过升温过程的粗化长大(与相邻纳米颗粒合并), 尺寸达到常规块体尺度后, 其熔化温度也就达到了同质块体材料A的熔点TA.所以, 对于纳米结构材料中的A纳米颗粒来讲, 在T1温度时, 实际是发生两个过程, 一是A纳米颗粒本身的熔化过程, 另一是A纳米颗粒(与其周围纳米颗粒A或B发生晶界迁移、合并)的粗化长大转变过程, 原因在于纳米结构材料中的纳米粒子是处于相邻粒子的束缚态中, 其熔化过程必然受到相邻纳米粒子的影响, 而对于自由态(单个纳米颗粒)的纳米颗粒, 则没有粒子的长大过程.
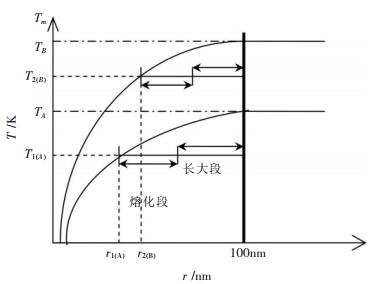 |
| 图 1 纳米结构材料熔化过程示意图 |
本文探讨铁液中的Al2O3纳米颗粒的熔化过程与上述纳米材料的熔化过程存在很多相同之处, 也有不同之处.在此基于以下3点来对Al2O3纳米颗粒在铁液中的熔化进行分析:首先, Al2O3纳米颗粒熔化过程所处的环境是铁液, 而不是通常测定物质熔点的空气环境, 为了对比, 后文同时计算了空气中Al2O3纳米颗粒的熔化温度; 第2, Al2O3纳米颗粒相当于自由态(单个纳米颗粒)的纳米颗粒, 不是纳米结构材料, 所以对于Al2O3纳米颗粒熔化过程的探讨, 不考虑纳米粒子长大、尺寸变化而带来熔化温度的升高问题; 第3, 此处只讨论Al2O3纳米颗粒的熔化, 而由于铁液作用带来的溶解问题已在前文阐述.
2.2 Al2O3纳米颗粒的熔化温度推导及计算根据热力学凯尔文(Kelvin)[12]公式, 微小颗粒的蒸气压与半径之间有以下关系:
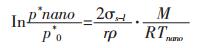
|
(11) |
式(11)中p*nano为纳米颗粒的饱和蒸气压; p*0为常规块体材料的饱和蒸气压; σs-l为纳米颗粒熔化时的固-液界面张力; r为纳米颗粒半径; ρ为颗粒密度; M为颗粒物质的分子量; Tnano为纳米颗粒的熔化温度; R为理想气体常数.
对于纯物质熔化时的固、液两相平衡, 克莱贝隆(Clapeyron)方程描述了物质所处的外压对其熔点的影响:
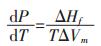
|
(12) |
式(12)P中为纯物质熔化平衡时的外压; T为纯物质的熔化温度(熔点); ΔHf为纯物质的摩尔熔化热; ΔVm为熔化时的摩尔体积变化.该式表明了纯物质熔化时外压对其熔点的影响, 外压越低则熔点越低.由于物质熔化时其饱和蒸气压与外压相等, 方向相反, 所以式(12)又可以理解为:在相同外压下, 饱和蒸气压越大的物质, 熔化温度越低.因此, 将式(12)中的外压P用物质的饱和蒸气压p*代换, 则式(12)可以改写成式(13):
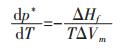
|
(13) |
式(13)中P*为纯物质熔化平衡时的饱和蒸气压, 其他符号含义同式(12).式(13)表明了纯物质熔化时饱和蒸气压对其熔点的影响, 这是与Clapeyron方程不同的.
以纳米颗粒和常规块体为上下限对式(13)进行定积分, 由于固体的摩尔体积远小于气体的摩尔体积, 可以忽略, 气体以理想气体处理, 则ΔVm=Vg-Vs≈ 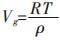
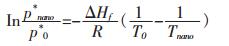
|
(14) |
式中T0为常规块体材料的熔化温度.
联立式(11)与式(14)可得:
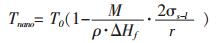
|
(15) |
从式(15)可以看出, 纳米颗粒的熔化温度与纳米颗粒半径r、固-液界面张力σs-l、摩尔熔化热ΔHf、颗粒密度ρ以及分子量M有关.
由于ΔVm=M/ρ, 所以式(15)又可表示成如下式(16)形式, 这与Couchman P R等人[13]关于材料尺寸与熔化温度关系的研究结果是一致的.
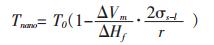
|
(16) |
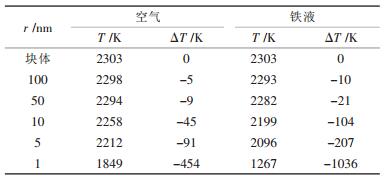
利用式(15)可以计算不同粒径的Al2O3纳米颗粒在空气、铁液中的熔化温度.表 2为计算所用到的相关数据[14], 由于温度对ΔHf影响较小, 视ΔHf为常量; 对于空气中的Al2O3纳米颗粒, 其熔化时的固-液界面张力为σs-l=σAl2O3, s-空气-σAl2O3, l-空气=0.21对于铁液中的Al2O3纳米颗粒, 其熔化时的固-液界面张力为σs-l=σAl2O3, s-铁液-σAl2O3, l-铁液=0.48.将表 2数据及空气、铁液中的σs-l数据待入式(15), 计算出不同粒径的Al2O3纳米颗粒在空气或铁液中的熔化温度, 如表 3所示.
| 表 2 Al2O3纳米颗粒的熔化温度计算所用数据 |
 |
| 点击放大 |
| 表 3 纳米Al2O3在空气及铁液中的熔化温度计算值 |
 |
| 点击放大 |
利用表 3数据绘制出纳米Al2O3的熔化温度(熔点)随半径的变化趋势如图 2所示.从表 3及图 2可以得出, 随着Al2O3纳米颗粒粒径减小, 其熔化温度逐渐降低, 粒径越小, 熔化温度下降的幅度越大, 而且, 相同粒径的纳米Al2O3颗粒在铁液中的熔化温度低于其在空气环境中的熔化温度.另外, 随着Al2O3纳米颗粒粒径不断增大, 其在空气和铁液中的熔化温度差异不断减小.
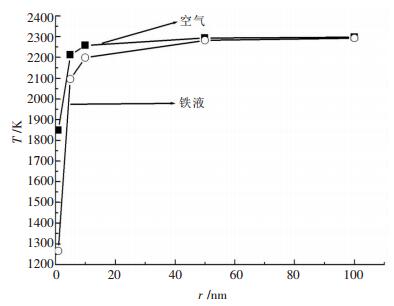 |
| 图 2 空气和铁液中纳米Al2O3颗粒半径与熔化温度(熔点)关系 |
3 结论
由于纳米颗粒的小尺寸效应, 导致其热力学性质不同于常规尺度材料, 本文尝试用近似计算纳米颗粒的界面能增加量的方法探讨了纳米Al2O3颗粒在铁液中的溶解平衡和熔化温度(熔点)问题, 得出以下几点结论:
(1) 纳米Al2O3在铁液中的平衡溶度积随颗粒半径的减小而逐渐增加, 而且颗粒越小, 平衡溶度积增加的幅度越大, 计算表明半径为0.1nm的Al2O3颗粒比块体Al2O3的平衡溶度积增加11.71%.
(2) 纳米Al2O3的熔化温度(熔点)随颗粒半径的减小而逐渐降低, 颗粒越小, 熔化温度降低的幅度越大, 且相同粒径的纳米Al2O3在铁液中的熔化温度低于其在空气中的熔化温度, 计算表明半径为1nm的Al2O3颗粒在空气和铁液中的熔化温度分别为1849K和1267K, 比块体Al2O3的熔化温度分别下降了454K和1036K.
(3) 用近似计算纳米颗粒的界面能增加量的方法可以给出纳米颗粒溶解与熔化热力学变化的基本趋势, 但计算结果存在一定误差, 目前较为恰当的方法是采用分子动力学方法模拟计算其热力学性质, 这是下一步应深入研究的问题.
| [1] |
卜勇, 胡本芙, 尹法章, 等. 低碳钢中以氧化物为核心针状铁素体的形成[J].
北京科技大学学报, 2006, 28(4): 357–360.
|
| [2] |
王巍, 付立铭. 夹杂物/析出相尺寸对晶内铁素体形核的影响[J].
金属学报, 2008, 44(6): 723–728.
|
| [3] |
王国承, 谢君阳, 鲍宇飞, 等. 添加纳米TiN颗粒对55SiMnMo钢性能的影响[J].
炼钢, 2010, 26(5): 60–64.
|
| [4] |
雷毅, 刘志义, 李海. 低碳型钢中添加ZrC粒子获得超细晶粒的研究[J].
钢铁, 2002, 37(8): 58–60.
|
| [5] |
王国承, 黄浪, 谢君阳, 等. 添加Al2O3纳米粉对中空钢55SiMnMo力学性能与夹杂物的影响[J].
特殊钢, 2008, 29(1): 19–21.
|
| [6] |
Hill T L.
Thermodynamics of Small Systems (Vol.Ⅰ)[M]. New York: A. Benjamin, NY, 1963.
|
| [7] |
Hill T L.
Thermodynamics of Small Systems (Vol.Ⅱ)[M]. New York: A. Benjamin, NY, 1964.
|
| [8] |
王国承, 王铁明, 李松年, 等. 高温纯铁熔体中外加氧化铝纳米粉的研究[J].
北京科技大学学报, 2007, 29(6): 578–581.
|
| [9] |
谢丹, 齐卫宏, 汪明朴. 金属纳米微粒熔化热力学性能的尺寸形状效应[J].
金属学报, 2004, 40(10): 1041–1044.
DOI: 10.3321/j.issn:0412-1961.2004.10.007. |
| [10] |
苏品书.
超微粒子材料技术[M]. 台湾: 复汉出版社, 1989.
|
| [11] |
张立德, 牟季美.
纳米材料和纳米结构[M]. 北京: 科学出版社, 2001.
|
| [12] |
梁英教.
物理化学[M]. 北京: 冶金工业出版社, 1992.
|
| [13] |
Couchman P R, Jesser W A. Thermodynamic Theory of Size Dependence of Melting Temperature in Metals[J].
Nature, 1977, 269(6): 481–483. |
| [14] |
陈家祥.
炼钢常用图表数据手册[M]. 北京: 冶金工业出版社, 1984.
|
 2011, Vol. 2
2011, Vol. 2
