| 矿井通风系统可靠性数值分析 |
2. 云南力合矿山工程设计有限公司,昆明 650021
2. Yunnan All Power Mining and Construction Design Co., Ltd., Kunming 650021, China
矿井通风系统可靠性的高低对矿井安全生产有着直接的影响.国内外自20世纪80年代以来,已取得了初步的研究成果[1-4].但由于问题本身的复杂性,还有许多问题尚未解决.矿井通风系统可靠性研究应在充分考虑以下几个特点的基础上进行.
(1)矿井通风系统是由风机、分支和通风构筑物三者组成的有机整体,在讨论矿井通风系统可靠性时,应充分考虑各单元的特点以及各单元之间的相互联系和相互制约;
(2)各通风构筑物单元在使用过程中的可靠性是相对的、动态变化的,其在某一时刻的可靠度不仅依赖于当时构筑物所处的状态,也与预计的剩余服役期有关;
(3)各分支的风量在系统结构不变时,不仅与风阻和风压有关,而且与风机和通风构筑物当时所处的状态有关.
1 分支的可靠性分支可靠性定义为:在矿井通风网络结构不变的条件下,在规定的时间内某一分支i的风量值能够保持在一个合理的范围之内的概率,称为该分支的可靠度,记为Ri.并相应地称该分支在任意时刻能保持其风量值在一个合理的范围之内的概率为该分支的有效度,记为Ai.
以Qi(t)表示实际情况下第i分支在t时刻的风量值,Qi(0)表示在风机和通风构筑物都稳定可靠的前提下第i分支的风量值.根据安全规程规定或分支用风需求确定两个风量限定值Wi(1)和Wi(2),当第i分支满足
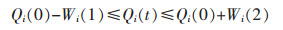
|
(1) |
则第i分支正常,否则第i分支为不正常.因此第i分支的有效度Ai可表示为

|
(2) |
通常,矿井通风网络的分支可靠度不仅是指风流的稳定程度或抗干扰能力,它与下列因素密切相关:①风流稳定性,角联网络分支造成的风流反向的可能性,风机的不稳定运行,井下提升运输设备因素等对风流运动的瞬时扰动现象;②调节设施工作的可靠性以及失效状态可能产生的危害程度和范围;③分支中的有毒性、窒息性和爆炸性气体与粉尘含量,一旦超限将使局部网络暂时失效;④漏风情况,风流的质量状况以及气候条件等.
由文献[5-8]可推导出,Qi(t)保持在闭区间[Qi(0)-Wi(1),Qi(0)+Wi(2)]内的概率(即第i分支的可靠度)为

|
(3) |

|
(4) |

|
(5) |
Ri值即为在综合考虑了分支风阻的随机扰动及通风构筑物的可靠性等因素后,第i条分支的风量保持在[Qi(0)-Wi(1),Qi(0)+Wi(2)]范围内的概率,即第i条分支的可靠度.
2 风机的可靠性可用一般可修系统的可靠性计算方法来评价风机的可靠性[9-12].
对于单台风机若其寿命遵从指数分布1-e-λt,t≥0,故障后的修理时间也遵从指数分布1-e-μt,t≥0.当两个随机变量相互独立,且故障部件修复后的寿命分布与新部件相同时,单台风机的有效度为

|
(6) |
对于主扇,根据矿山安全规程的要求,都需要设备用风机(一般只有电机备用).可将主扇单元看作用两个相同型号部件组成的冷储备系统,若这两台风机寿命和故障后修理时间均服从负指数分布,则主扇单元的有效度为

|
(7) |
一般情况下,若某矿备有n台相同型号的主扇,正常情况下需要k台主扇工作,当工作的某台主扇发生故障后,则将剩余的n-k台中的某台启动,此时可将主扇单元视为k/n(G)表决系统,若每台主扇的寿命分布和故障后的修理时间分布均服从负指数分布,则主扇单元的有效度为
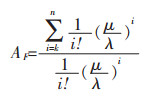
|
(8) |
通风构筑物的类别不同,其可靠度的定义和计算方法亦不同.
3.1 截断风流的通风构筑物可靠性对于风门、挡风墙、风帘截断风流的通风构筑物,其主要功能就是将风流截断,阻止风流通过.其可靠度定义为:对于截断风流的通风构筑物,在某一时刻t完成截断风流的能力,称为该构筑物在t时刻的可靠度.若Rs1(t)表示这类构筑物在t时刻的可靠度,则有

|
(9) |
式(9)中,Qi(t)为截断风流的通风构筑物在t时刻的漏风量,m3/s;QSj(t)为截断风流的通风构筑物入风侧的设计风量,m3/s.其值为网络解算所得的风量值,此值不随构筑物的服役期t的变化而变化,而只与t时通风系统的网络结构有关.
新建截断风流的通风构筑物总有一定的漏风量,其值可通过实测而得,以Qi(0)表示.则新建截断风流的通风构筑物的可靠度为

|
(10) |
该通风构筑物在使用过程中,随着其服役期t的增长,由于不断受到外部环境及构筑物本身的逐渐老化等因素的影响,在不维修的情况下,其漏风量会逐渐增加.在t时构筑物的漏风量Qi(t)可以按式(11)评估

|
(11) |
式(11)中,Ci(t)是与构筑物在服役期内的经历有关的系数.
3.2 通过风流的通风构筑物可靠性风桥等通过风流的通风构筑物的功能就是要使风流顺利地通过.可将其可靠度定义为:对于通过风流的通风构筑物在某一时刻t,其能使风流顺利通过的能力称为该构筑物在t时刻的可靠度.若以RS2(t)表示这类构筑物在t时刻的可靠度,则有

|
(12) |
式(12)中,Qi(t)为通过风流的通风构筑物入风侧的风量,m3/s,即为网络解算所得之风量值;Q0(t)为该通风构筑物出风侧的风量值,m3/s.
新建构筑物在风流通过的过程中总有一定的损失,即有

|
(13) |
即其风量损失为

|
(14) |
在不维修的情况下,随着构筑物服役期t的增长,QS(t)逐渐增大.QS(t)可以实测,也可以按式(15)评估

|
(15) |
式(15)中,CS(t)是与构筑物在使用期内的经历等因素有关的系数.
3.3 调节风流的通风构筑物可靠性对于风窗等调节风流的通风构筑物,其可靠度定义为:对于调节风流的通风构筑物在某时刻t,其能通过的风量符合设计要求的程度,称为该构筑物的可靠度.并以RS3(t)表示.据此定义有

|
(16) |
式(16)中,Qp(t)为t时刻该类构筑物的实际过风量,m3/s;Qd为设计构筑物的过风量,m3/s.Qp(t)值可以实测获得,也可利用与式(15)相似的公式评估而得.
4 矿井通风网络的可靠性对于某一矿井通风网络,以m表示其节点个数,P表示其通路矩阵,A表示其关联矩阵,I为单位矩阵.若令C=A+I,取矩阵C中元素Cm1的余子式,并采用逻辑乘和逻辑加的运算方法对这一余子式展开,则得到从起始节点(进风井口)到终止节点(排风井口)的全部有向通路.
若以pij描述分支ej是否在第i通路上,并令

|
(17) |
则可求得该矿井通风网络的通路矩阵为

|
(18) |
式(18)中,k为该网络的通路数;n为该网络的分支数.
若以Rnet表示矿井通风网络的可靠度,则有

|
(19) |
式(19)中,pi表示矿井通风网络的第i条通路.
式(19)是网络可靠度的计算式,它与网络中进风点和出风点间的最小通路密切相关.但由于最小通路间的不相斥性,具有大量公共边,使得网络可靠度的计算相当困难.为了改进算法,采用不交型布尔代数算法.通过不交型布尔代数的化简、展开吸收、归并等运算,使得最小通路间不含有公共边.这样对于通路,可按互不相容事件求概率,得到网络可靠度.
5 矿井通风系统可靠度优化分配采用一个可行的状态S=(R,Q,H),使得S在满足按需分风和经济性的条件下,可靠度达到最大,这个问题可用下列非线性规划进行描述[13].

|
(20) |
式(20)中,S1和S2分别为固定风量分支集和风机分支集;bij为该网络回路矩阵B中的元素;Ei为第i台风机的目标流线分支集;Hfi为第i台风机的压力上限值.
式(20)的目标函数比较复杂,直接求解困难较大,应设法把目标函数进行简化.由式(4)和式(5)不难看出,要使得每个Ri都尽可能的大,只有让均值μ*i尽可能地接近Qi(0),让方差σ*i尽可能小,而由μj(1)、μj(2)、σj(1)和σj(2)的不确定性,也只有让每个αij和βij的绝对值尽可能地小才行.根据已有研究结果[7-8],矿井通风网络的阻力定律、风量平衡定律和风压平衡定律可以综合写成下面的方程组.

|
(21) |
由隐函数存在定理知,如矿井通风网络处于平衡状态S0的Jacobi行列式不为零,即

|
(22) |
则式(21)在S0的某一邻域内存在唯一的连续偏导数解[14].

|
(23) |
由此可知,当J的绝对值充分大时,可使每个αij和βij的绝对值尽可能地小.式(20)的目标函数可以改为对J进行极大化.各分支风量一定时,调节各分支的风阻极大化J的优化模型如下:设已知各分支的风量为Q1(0),Q2(0),…,Qn(0),至少存在一棵生成树,使其所有余树枝风量不为零.从经济方面考虑,约定风机的压力上限分别为Hf1,Hf2,…,HfF,则这时的优化模型为

|
(24) |
式(24)中,ΔRj为分支j的风阻增量;J(ΔR1,ΔR2,…,ΔRn)为Jacobi行列式;S3为不可调分支[15]集;Ei和S2同前,M=106,且

|
(25) |

|
(26) |

|
(27) |

|
(28) |

|
(29) |
图 1为某矿井通风网络,10条分支,6个节点.风机工作方式为抽出式,型号为4-72-11№20,转速为315r/min,风流上行流动.各分支对应的风阻值(N·s2/m8)为式(30),该风机的H-Q特性方程为式(31),分支4、8、9为固定风量分支,该网络无火灾时的风量分配为式(32)

|
(30) |

|
(31) |

|
(32) |
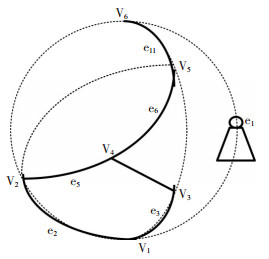 |
| 图 1 某矿井通风网络示意图 |
现分析火灾时各分支的风流稳定性.选一棵生成树,如图 2所示(实线部分).取Wi(1)=0.2Qi(0),Wi(2)=0.3Qi(0),μi(1)=μi(2)=0,σi(1)=0.04,σi(2)=1,i=1,2,…,10.上机计算求得各分支可靠度

|
(33) |
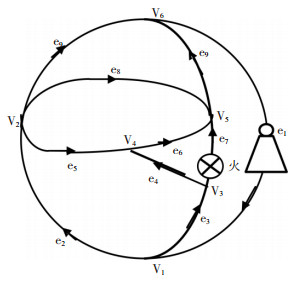 |
| 图 2 图 1网络的生成树 |
由可靠度知分支5风流最不稳定,分支9风流最稳定;固定风量分支中,分支4最不稳定,分支9最稳定.
当分支7发生火灾时,主干分支中的风量增加,旁侧分支中的风量减小甚至反向.与主干分支相交的分支4、6、8、9中,由可靠度可知分支4风流首先反向,分支6次之,分支8再次之,这与分支可靠度是对应的.解算结果证明由分支可靠度来判断风流稳定性是正确的.尽管分支5没有反向,但它的风流稳定程度受干扰最大,例如当Δt=1300℃时,分支5中风量变化率为401.40%,其他分支中风量变化率值均小于它.实际上,风流稳定性是风向和风量稳定性的总称.
| [1] |
徐瑞龙.
通风网络理论[M]. 北京: 煤炭工业出版社, 1993: 37-179.
|
| [2] |
马云东, 孙宝铮.
矿井广义可靠性设计理论[M]. 北京: 煤炭工业出版社, 1995: 109-119.
|
| [3] |
徐瑞龙, 刘剑. 井下通风构筑物的可靠性分析[J].
煤炭学报, 1992(3): 72–78.
|
| [4] |
董海燕. 矿井通风网络的可靠度分析[J].
系统工程理论与实践, 1988(3): 47–51.
|
| [5] |
赵梓成, 谢贤平. 矿井通风网络的可靠性理论研究[C]//全国非金属矿学术会议论文集. 武汉: 中国硅酸盐学会非金属矿专业委员会, 1988: 50.
|
| [6] |
谢贤平, 赵梓成. 矿井风流的稳定性分析[J].
有色矿山, 1992(5): 22–27.
|
| [7] |
谢贤平, 赵梓成. 矿井通风系统的可靠性分析[J].
昆明工学院学报, 1992(6): 11–17.
|
| [8] |
谢贤平. 矿井通风网络的可靠度计算[J].
工业安全与防尘, 1992(8): 5–9.
|
| [9] |
李世华, 向键.
矿井通风设备使用维修[M]. 北京: 机械工业出版社, 1990: 1-61.
|
| [10] |
白铭声.
矿井通风设备运行与组合设计[M]. 北京: 煤炭工业出版社, 1987: 80-88.
|
| [11] |
曹晋华, 程凯.
可靠性数学引论[M]. 北京: 科学出版社, 1986: 77-138.
|
| [12] |
孙晓, 卢新田, 于晓丹, 等. 风机系统可靠性分析[J].
吉林工业大学学报, 1995(2): 94–99.
|
| [13] |
蒂尔曼. 系统可靠性最优化[M]. 刘炳章, 译. 北京: 国际工业出版社, 1988: 9-19.
|
| [14] |
席少霖.
最优化方法[M]. 上海: 上海科学技术出版社, 1983.
|
| [15] |
赵梓成.
矿井通风计算与程序设计[M]. 昆明: 云南科技出版社, 1992: 126-134.
|
 2010, Vol. 1
2010, Vol. 1
