| FAPH在采场安全风险分析中权重分配的应用 |
2. 兰州资源环境职业技术学院,兰州 730021
2. Lanzhou Resources and Environment Voc-Tech College, Lanzhou 730021, China
由于各危险因素对金属地下矿山采场稳定性的影响程度是不同的,表现在它们各自的权重不一样.为了准确评判采场稳定程度,必须采用合适的方法确定采场危险因素的权重,在定量风险分析中对各要素权重分配的合理,取值的准确、科学与否直接关系着评判的最终结果.
目前常用的权重系数确定方法有:层次分析法(AHP)、相对差距合法、主成分分析法、秩和比法、全概率评分法、工神经网络、蒙特卡罗模拟综合评价法和模糊综合评判法等[1].综合这些方法,层次分析法是一种比较简单可行的决策方法,其主要优点是可以解决多目标的复杂问题,在定量和定性相结合中根据各个决策方案的标准权重数来判断决策方案的优劣,它能有效地解决很多难以完全用定量或定性方法解决的实际问题.
但层次分析法的关键环节是建立判断矩阵,判断矩阵是否科学、合理直接影响到AHP的效果,但在实际应用中AHP有以下缺点使其使用范围受到了制约[2-3].
(1) 检验判断矩阵是否具有一致性非常困难.检验判断矩阵是否具有一致性需要求判断矩阵的最大特征根λmax,看λmax是否同判断矩阵的阶数n相等.当阶数n较大时,精确计算λmax的工作量非常大.
(2) 当判断矩阵不具有一致性时需要调整判断矩阵的元素,使其具有一致性,这不排除要经过若干次调整、检验、再调整、再检验的过程才能使判断矩阵具有一致性.
(3) 检验判断矩阵是否具有一致性的判断标准:CR < 0.1缺乏科学依据.
(4) 判断矩阵的一致性与人类思维的一致性有显著差异.
1 FAHP方法原理及模型 1.1 FAHP方法概述模糊层次分析法(Fuzzy Analytic Hirearchy Process)改进了传统层次分析法存在的问题,提高了决策可靠性.FAHP有一种是基于模糊数,另一种是基于模糊一致性矩阵[4],本文讨论后一种.
下面介绍如何建立模糊互补判断矩阵、模糊互补判断矩阵权重的计算方法以及模糊互补判断矩阵的一致性判断方法.
1.2 FAHP的数学模型(1) 模糊判断矩阵的构建.在模糊层次分析法中,作为系统各因素之间的两两比较判断,采用的是两个相对比较因素的重要程度来定量化的,将比较的结果用矩阵A=(aij)n×n的形式,则矩阵A成为模糊判断矩阵,当A满足:aii=0.5,aij+aji=1其中i,j=1,2,….,n;称这样的判断矩阵为模糊互补判断矩阵[1].
在模糊互补判断矩阵的构建时,对于系统内的两要素两两比较相对重要程度时,通常采用表 1所示的0.1~0.9标度法[2]来定量.
| 表 1 0.1~0.9标度法一览表 |
 |
| 点击放大 |
依据表 1的重要性数字标度,对要素a1,a2,…,an相互比较,则得到如下模糊互补判断矩阵:
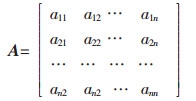
|
(2) 模糊互补判断矩阵的权重.文献[5]推导出了求解模糊互补判断矩阵权重的一种通用公式,带来了极大方便.该公式如下:
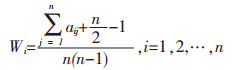
|
(1) |
(3) 模糊判断矩阵一致性验证.由上述公式求出的模糊互补判断矩阵权重是否合理,必须对其结果进行一致性检验.文献[6]对模糊矩阵的一致性验证进行了研究,推导出了较为容易实现的方法,即采用矩阵之间的相容性来验证模糊判断矩阵的一致性.相容性来验证模糊判断矩阵的一致性原则如下:
设矩阵A=(aij)n×n和B=(bij)n×n均为模糊判断矩阵,若满足:
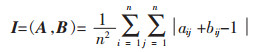
|
(2) |
则称A和B相容,I为相容指标.
设W=(W1,W2,…,Wn)T是模糊判断矩阵A的权重向量,其中
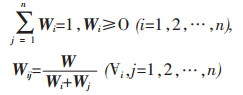
|
(3) |
则称n阶矩阵W*=(Wij)n×n为判断矩阵A的特征矩阵.
当模糊判断矩阵的相容性指标I(A,W*)≤α(α为决策者的满意度指标)时,认为判断矩阵为满意一致性的.α越小说明决策者对模糊判断矩阵的一致性判断要求越高,一般可取α=0.1.
在实际应用中,是由多个专家(假设为m)给出同一要素集X上的比较判断矩阵A(k),它们均是模糊互补的判断矩阵,则得到的权重集合W(k)Ak=(aij)n×n(k),W(k)=(W(k)1,W(k)2,…,W(k)m)其中k=1,2,3, …,m;
对于权重集合W(k)进行一致性判断时,需满足以下两个条件:①检验m个判断矩阵Ak=的满意一致性I(Ak,W(k))≤α,k=1,2,3, …,m;②检验判断矩阵间的满意相容性I(Ak,Aι)≤α,k≠ι,ι,k=1,2,3, …,m;
即只要当①与②同时满足时,m个权重集的均值作为要素X的权重分配系数是合理和可靠的[7].
2 金属地下矿山采场安全风险各主控因素权重的确定根据上述对目前权重系数确定的方法相互比较,本文就选择比较切合矿山实际应用领域的层次分析法,对金属地下矿山采场安全风险的4个主控因素的权重系数进行定量分析.
2.1 建立金属地下矿山采场安全风险层次模型影响采场稳定性的因素很多、很复杂.但根据大量实践经验来看,各因素的影响程度是不同的:有些因素影响程度大一些,而有些因素影响程度小一些.因此,有必要通过分析,简化与综合各危险影响因素.
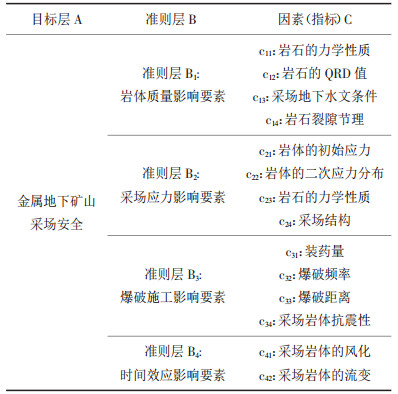
地质与构造、岩层与岩性以及地下水主要影响着采场岩体的岩体质量;岩体初始应力以及采场结构主要影响着采空区周围二次应力分布状况;开采工艺(主要是爆破工艺)也会显著影响采场的稳定状况;且随着时间的推移,由于岩体风化和流变现象(其与时间有关,故称之为时间效应),采场也越来越处于不稳定状态.由上所述,影响采场稳定的危险因素可归纳为:采场岩体质量、采场二次应力分布、爆破冲击和时间效应4个主控因素协同作用影响着金属地下矿山采场的安全[8].金属地下矿山采场安全风险分析各主控要素层次见表 2,其结构组织见图 1.
| 表 2 金属地下矿山采场安全风险分析各主控要素层次 |
 |
| 点击放大 |
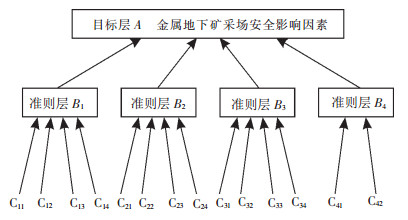 |
| 图 1 金属地下矿采场安全影响因素机构组织 |
2.2 构建模糊判断矩阵
相对于影响金属地下矿采场安全的4个评价准则,假设由两个或多个领域专家依据表 1打分的方法分别对各因素作两两比较判断,得到权重模糊互补判断矩阵A1、A2:
设专家1给出的权重模糊互补判断矩阵为
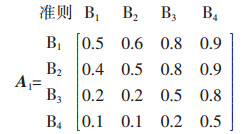
|
根据式(1),A1的权重向量为W1=(0.317 0.3 0.225 0.158)
根据式(3),A1的特征矩阵计算结果为
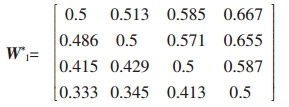
|
据式(2),A1和W1*的相容性指标为:I(A1,W1*)= 0.04 < 0.1,故可认为模糊判断矩阵A1是满意一致的,即权重集W1的分配是合理的.
设专家2给出的权重模糊互补判断矩阵为
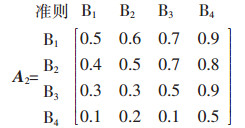
|
同理可得,A2的权重向量为W2=(0.308 0.292 0.25 0.158)
A2的特征矩阵计算结果为:
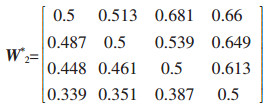
|
A2和W2*的相容性指标为:I(A2,W2*)=0.04 < 0.1,故可认为模糊判断矩阵A2是满意一致的,即权重集W1的分配是合理的.
再验证模糊判断矩阵A1和A2的满意相容性:I(A1,A2)=0.06 < 0.1,故两者是满意相容的.
由上述对模糊互补判断矩阵的讨论可知,将权重集的均值作为因素集的权重分配向量是合理和可靠的,则综合两个专家的意见后权重向量可表示为:
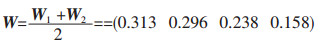
|
当有多个专家参与评判时,可以采用类似的方法进行模糊矩阵的一致性与相容性检验.
2.3 指标指数矩阵的建立对于影响金属地下矿采场安全的4个评价准则建立模糊互补判断矩阵.由专家依据表 1打分的方法,对要素作两两比较判断,得到模糊矩阵R.为论述简单,这里仅给出一个专家评判矩阵.对于多个专家参与的评判,则需要用与2.2节中相似的方法进行模糊判断矩阵间的满意相容性检验.
B1采场岩体质量影响因素的模糊判断矩阵:

|
B2采场二次应力分布影响因素的模糊判断矩阵:
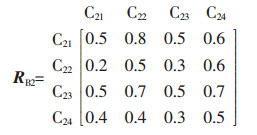
|
B3爆破冲击影响因素的模糊判断矩阵:
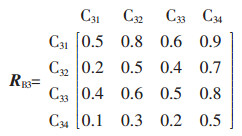
|
B4时间效应影响因素的模糊判断矩阵:
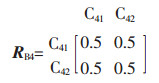
|
根据上述4个模糊判断矩阵,根据式(1)可算出单个影响因素的权重向量:
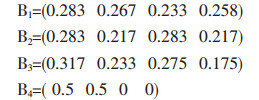
|
并对上述4个向量进行比较判断的满意一致性检验.可以验证将其作为决策依据是可靠的,此时:
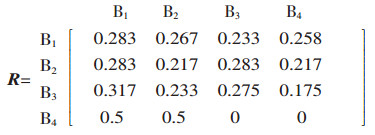
|
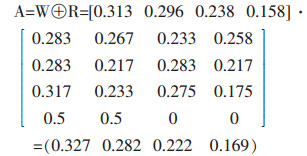
影响金属地下矿山采场安全的4个主控因素权重的总排序结果为:
|
上式中的算子采用模糊数学的加权平均值(⊕,·)运算法则,其优点是可以兼顾到各个因素对系统的影响,体现了系统整体特征.按照最大隶属度原则,在影响金属地下矿山采场安全的4个主控因素的权重大小依次为4个影响因素的优选排序为:B1采场岩体质量:0.327;B2采场二次应力分布:0.282;B3爆破冲击:0.222;B4时间效应:0.169.
3 结语结合模糊层次分析法的数学模型对金属地下矿山采场安全风险分析中4个主控要素的权重进行了总体评价,对影响采场安全的各主控因素的权重进行定量化,使金属地下矿山采场安全风险模型综合化评价从定性分析提升至定量分析的高度,为金属地下矿山对采场安全采取的决策提供更科学合理的依据.
| [1] |
王晖, 陈丽, 陈垦, 等. 多指标综合评价方法及权重系数的选择[J].
广东医学院学报, 2007, 10(5): 583–588.
|
| [2] |
李柏年.
模糊数学及其应用[M]. 合肥: 合肥工业大学出版社, 2007: 130-134.
|
| [3] |
吕跃进. 基于模糊一致矩阵的模糊层次分析法的排序[J].
模糊系统与数学, 2002, 16(2): 79–85.
|
| [4] |
张吉军. 模糊层次分析法(FAHP)[J].
模糊系统与数学, 2000, 14(2): 80–88.
|
| [5] |
陈泽水. 模糊互补判断矩阵排列的一种算法[J].
系统工程学报, 2001, 16(4): 311–314.
|
| [6] |
陈华友, 赵佳宝. 模糊判断矩阵的相容性研究[J].
运筹与管理, 2004, 13(1): 44–47.
|
| [7] |
陈泽水. 模糊判断矩阵的相容性及一致性研究[J].
解放军理工大学学报, 2002, 3(2): 94–97.
|
| [8] |
王宝山, 黄志伟, 谢本贤, 等. 金属地下开采采场灾害预警系统的研究[J].
湖南科技大学学报:自然科学版, 2006, 21(4): 62–64.
|
 2010, Vol. 1
2010, Vol. 1
