| 隐伏多空区对露天边坡稳定性的影响研究 |
2. 北京科技大学土木与环境工程学院,北京 100083
2. Civil and Environment Engineering School, University of Science and Technology Beijing, Beijing 100083, China
露天开采形成的边坡不仅要受到人为因素的影响,而且更重要的是受到岩体性质、地形、水以及地质构造的影响,其中地质构造中存在隐伏多空区的情况对边坡稳定性的影响较复杂。国内外对露天边坡稳定性分析方面作了大量的研究,取得了许多研究成果[1-2]。目前在分析露天开采边坡下存在隐伏多空区时,常用的方法有:塑性极限法[3]、极限平衡法[4]、强度折减法[5-6]、解析法[7]等。本文以某露天开采边坡工程为背景,分别采用AutoCAD强大的绘图功能、ANSYS快速的划分网格功能和FLAC3D软件强大的数值模拟分析功能,以及Mohr-coulomb破坏准则对此工程进行了计算机模拟,分析了两种不同位置情况下隐伏多空区对露天边坡的影响,弥补了FLAC3D不能定量分析的不足,对边坡的数值稳定性分析进行了有益的探索。
1 三维数值模拟模型 1.1 三维模型的建立本工程的基本三维模型是通过AutoCAD建立的,然后通过AutoCAD的输出功能将模型导入ANSYS,进而在ANSYS中对模型进行网格划分,最后在FLAC3D中对导入的模型进行计算[8]。模型上边界、下边界、高度的尺寸分别为190 m、270 m、160 m,隐伏多空区高为30 m、单个空区宽为2 m、两个空区间隔为1 m.本工程设计了两种不同的模拟方案:第一种方案隐伏空区位于整个模拟边坡的下部,模型共11310个网格,4057个节点,如图 1所示;第二种方案隐伏空区位于整个模拟边坡的上部,模型共11375个网格,4083个节点,如图 2所示。
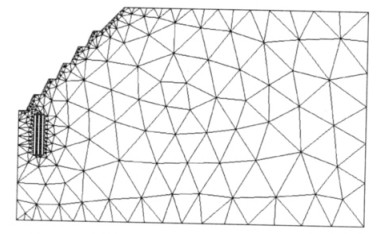 |
| 图 1 隐伏多空区露天边坡计算模型方案一 |
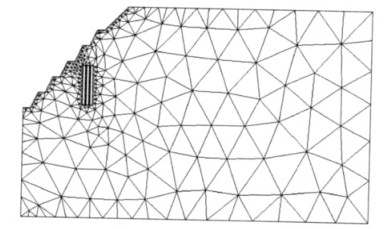 |
| 图 2 隐伏多空区露天边坡计算模型方案二 |
1.2 模型的荷载和边界条件
三维模型对初始的地貌做了简单的还原, 从而得到了更为接近实际情况的原始应力场,即只考虑由岩体自重产生的应力场。本工程模型除了上表面为自由面外,其余均为固定约束边界。
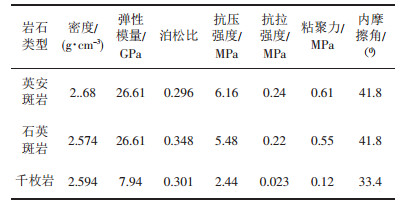
1.3 岩体物理力学参数在岩体物理力学参数的选取方面,以某研究所的研究资料为依据。各种参数见表 1。
| 表 1 岩体物理力学参数 |
 |
| 点击放大 |
2 数值模拟结果分析
在进行数值模拟计算时,依据露天边坡下隐伏多空区两种不同的位置进行分析。分析时按前述约束条件,只考虑在重力作用下进行Mohr-coulomb破坏准则的弹塑性求解。以下就位移情况、应力情况和Mohr-coulomb圆进行分析。
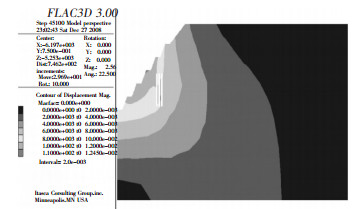
2.1 位移分析图 3和图 4分别为两种模拟方案下边坡位移等值云图,空区位于下部时边坡最大位移为11.2 mm,空区位于下部时边坡最大位移为12.4 mm,可见位置不同的空区对边坡的最大位移没有产生较大影响,但是在第一种方案下的平均位移比第二种方案小,且产生位移的区域也比第二种方案少。同时在空区内部的位移情况两种方案也有所不同,前者位移范围一般在1-4 mm,后者位移范围则在6-8 mm。由此可见,隐伏多空区的位置对边坡位移没有产生较大的影响。
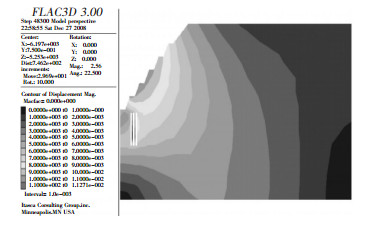 |
| 图 3 方案一位移等值云图 |
 |
| 图 4 方案二位移等值云图 |
2.2 应力分析
图 5和图 6分别为两种模拟方案下边坡最大主应力等值云图,从图中可以看出:当空区位于下部时,边坡在每个台阶边缘和空区矿柱主要受拉应力作用,其最大值为0.018 MPa;当空区位于上部时,空区矿柱及其周围岩体也主要受拉应力作用,其最大值为0.029 MPa。在空区位于下部时,其矿柱周围岩体主要受压应力作用,而在空区上部时则其矿柱周围岩体主要受拉应力作用。由此可知,隐伏多空区的不同位置是引起边坡内岩体应力变化的高敏感性因素[9]。
 |
| 图 5 方案一最大主应力等值云图 |
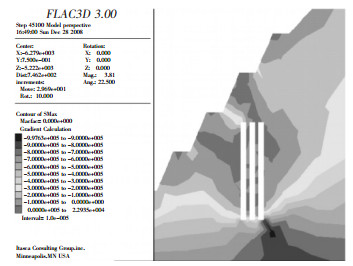 |
| 图 6 方案二最大主应力等值云图 |
2.3 Mohr-coulomb圆定量分析
摩尔强度理论是岩土力学用得最多的一种理论,该理论认为材料内某一点的破坏主要取决于它的大主应力和小主应力,而与中间主应力无关。根据各种不同应力比的大小主应力在τ-σ平面上绘制一系列的应力圆称为Mohr圆。根据Mohr圆可以方便地看出不同位置的应力情况[10]。
本文从两种方案中分别选取了边坡台阶中剪切应力最大的区域作为分析对象,如图 7和图 8所示。
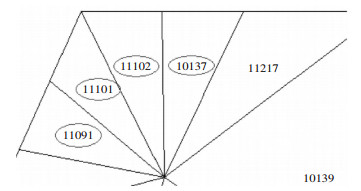 |
| 图 7 方案一区域单元号示意图 |
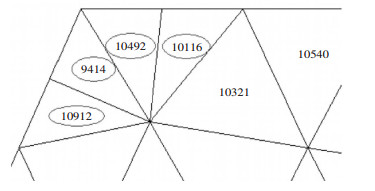 |
| 图 8 方案二区域单元号示意图 |
通过Excel绘制的Mohr圆[8],可以清楚地从定量分析的角度来判断各单元剪切破坏的程度,如图 9和图 10所示。
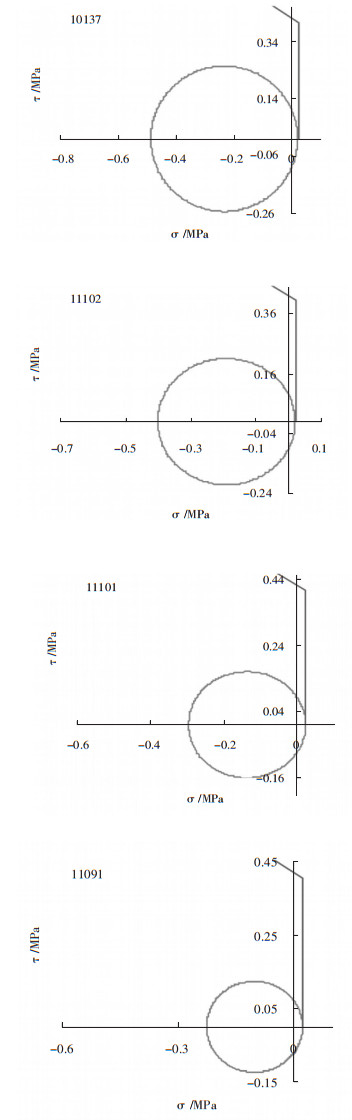 |
| 图 9 方案一各单元计算Mohr圆 |
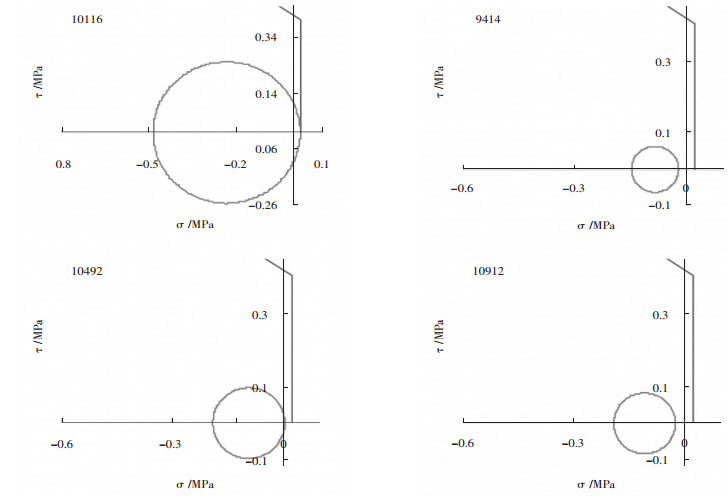 |
| 图 10 方案二各单元计算Mohr圆 |
从方案一的Mohr圆上看出,各单元均未达到极限剪切破坏状态,但都已经达到极限拉应力破坏状态。说明这种方案的边坡可能因拉应力破坏从而失稳。方案二中只有10116#单元达到极限拉应力破坏状态,其它单元均未达到极限剪切破坏状态和极限拉应力破坏状态。说明这种方案的边坡相对来说是比较稳定的。
3 结论通过对两种方案下边坡最大位移、最大主应力以及选取的剪切应力最大的区域单元Mohr圆比较,分析了两种不同位置情况下多隐伏空区对露天边坡的影响,可知位置不同的隐伏多空区对露天边坡会产生一定的影响:当隐伏多空区位于边坡岩体上部时会因拉应力达到极限状态而失稳;当隐伏多空区位于边坡岩体下部时相对来说比较稳定。本文从Mohr圆角度定量分析了边坡剪切破坏程度,弥补了FLAC3D不能定量分析的不足,对边坡的数值稳定性分析进行了有益的探索。
| [1] |
张友锋, 袁海平. FLAC3D在地震边坡稳定性分析中的应用[J].
江西理工大学学报, 2008, 29(5): 23–26.
|
| [2] |
黄国平, 康斌. 边坡稳定性量化评价方法探讨[J].
江西理工大学学报, 2007, 28(1): 51–53.
|
| [3] |
陈祖煜, 汪小刚, 杨健, 等.
岩质边坡稳定分析原理、方法、程序[M]. 北京: 中国水利水电出版社, 2005.
|
| [4] |
蔡美峰, 何满潮, 刘东燕.
岩石力学与工程[M]. 北京: 科学出版社, 2002.
|
| [5] |
谷栓成, 徐学文. 高边坡加固工程有限元稳定性分析[J].
采矿与安全工程学报, 2006, 23(6): 201–204.
|
| [6] |
赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J].
岩石力学与工程学报, 2003, 22(2): 254–260.
|
| [7] |
祝方才, 曹平, 万文. 基于轴对称厚板模型的浅埋空区顶板安全厚度[J].
采矿与安全工程学报, 2006, 23(1): 115–118.
|
| [8] |
廖秋林, 曾钱帮, 刘彤, 等. 基于ANSYS平台复杂地质体FLAC3D模型的自动生成[J].
岩石力学与工程学报, 2005, 24(6): 1010–1013.
|
| [9] |
韩现民, 李占金, 甘德清, 等. 露天转地下矿山边坡稳定性的数值模拟与敏感度分析[J].
金属矿山, 2007(6): 8–12.
|
| [10] |
徐志英.
岩石力学[M]. 北京: 水利电力出版社, 1993.
|
 2009, Vol. 23
2009, Vol. 23
