| 越障机器人运动学分析与仿真 |
越障机器人的研究,对扩展机器人的作业空间,在人不能到达或不便到达的环境中进行作业,具有重要的意义。越障机器人还可用于工业中的一些险难作业,不仅可提高产品的质量与产量,而且对保障人身安全,改善劳动环境,减轻劳动强度,提高劳动生产率,节约原材料消耗以及降低生产成本,有着十分重要的意义。
越障机器人的种类很多,但大多还是面向障碍类型相对单一的实验室环境下的障碍条件,而面向现场环境下的越障工业机器人的研制及其越障过程的运动学分析还较少。由于工业回转窑的窑衬在清理时,其作业环境非常危险,作业条件非常恶劣,窑衬内部表面形状呈凹凸不平。因此有必要研制一种针对回转窑内部窑衬的障碍类型及其分布规律的越障机构,并从理论上分析机器人在跨越障碍时的运动学特性,为回转窑窑衬清理机器人的设计以及越障效能分析提供技术支撑。
1 越障机器人结构组成及越障原理分 1.1 机器人结构组成由于回转窑的内部形状为毫无分布规律的波浪形,内部作业空间狭小,为了保证清窑机器人在作业时的稳定性,可以采用四轮驱动的行走装置,并且在每个行走装置上附加一套行星轮式越障机构,使机器人越障碍时相互干涉较小,且机器人的重心波动最小。清窑越障机器人的结构如图 1所示。
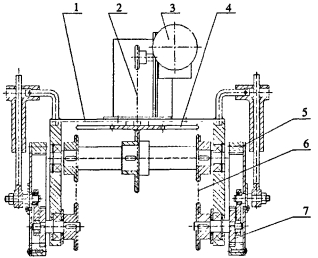 |
| -机架;2-第一级传动装置;3-驱动装置;4-转向装置;5-行走轮装置;6-第二级传动装置;7-行星轮装置 图 1 越障机器人总体结构 |
在图 1中,机器人的驱动装置将动力通过第一级、第二级传动装置传给行星轮装置,由行星轮将扭矩传递到行走轮上;当行走轮碰到障碍物时,通过行星轮的爬越实现越障。
1.2 越障工作原理分析越障机器人的越障机构简图如图 2所示。驱动轴Ⅰ安装在机架上,行星轮2安装在该轴上。内齿轮轴Ⅱ安装在行走轮5上,并通过连杆3与轴Ⅰ连接而组成行星轮越障机构。行走过程中扭矩通过轴Ⅰ传递到行星轮2上,当行走在没有障碍的地面上时,行星轮2处在行走轮5的最低点位置,并驱动行走轮5绕轴Ⅱ转动。
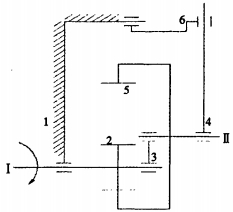 |
| 、Ⅱ-轴;1-基本构件;2-驱动轮;3-连杆;4-上升杆;5-行走轮;6-导向套 图 2 机器人越障机构原理图 |
当行走轮5碰到障碍物时,行走轮停止滚动,而行星轮2则沿着行走轮内齿上升,由于轴Ⅰ与机架连接,从而带动整个机器人车身上升;当行星轮2沿着行走轮5的内侧转动爬到某一定高度时,行星轮推动行走轮绕着障碍物转动,使行走轮和机架爬越到障碍物的最高处。
越障碍机器人自由度为:
F=3n-2PL-PH
式中:n为除机架外的构件数量; PL为低副数量; PH为高副数量。
本越障机器人的构件数n=5,低副PL=6,高副PH=1,则越障碍机器人的自由度为2。
2 越障过程的运动学分析 2.1 模型简化与假设越障机器人在越障的过程中其运动关系非常复杂,在对机器人进行运动学分析时,为了便于建立机器人在越障过程中的运动学模型,需要进行以下简化与假设:①将机器人整个车身划分成4个质量均等的部分。② 4个部分的质量就集中在行星轮的质心上。③其他外在因素不影响机器人的运动。④行星轮质心的运动近似为机器人的运动。
鉴于以上简化和假设,越障机构运动学分析[1]就可看成是窑衬清理机器人的运动学分析。根据图 1结构所设计的清窑机器人,连杆3的质量m1=0.2 kg,行星轮的质量m2=14.8 kg,行走轮质量m3=4 kg,机器人总体质量m总=76 kg,所以每个轮子分担的质量为19 kg。
行星轮的半径r=31.5 mm,行走轮的半径R=79.5 mm。机器人的的最小驱动力F=55 N,扭矩等于m0=F R=55×79.5×10-3≈4.4 N·m。
2.2 越障运动学模型的建立由于越障过程非常复杂,很难用一个运动学方程描述越障机器人的运动过程。因此,将爬越障过程分为5个阶段[2-3],如图 3所示。
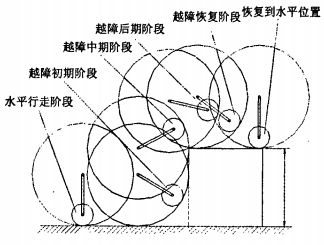 |
| 图 3 机器人越障过程 |
2.2.1 水平行走阶段
当机器人在水平地面行走,行星轮在行走轮的最低点驱动行走轮在水平地面上做纯滚动,行星轮的质心作水平运动。其运动学方程为:
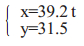
|
(1) |
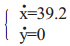
|
(2) |
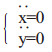
|
(3) |
当机器人碰到障碍物时,行走轮停止滚动,行星轮沿行走轮的内侧做圆周运动,同时绕着自身的质心做自转运动,当行星轮爬升到最高位置时,越障初期阶段结束。其运动学方程为:
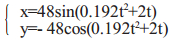
|
(4) |

|
(5) |

|
(6) |
当机器人越障初期阶段结束后,行星轮停止做圆周运动,只围绕其自身质心自转。在障碍物高度大于行走轮半径时,行走轮行星轮推动行走轮在障碍物垂直面上做纯滚动,当行走轮到达障碍物最高点,越障中期阶段结束。其运动学方程为:
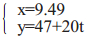
|
(7) |
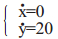
|
(8) |
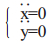
|
(9) |
行星轮沿行走轮内侧继续往上爬升,同时驱动行走轮绕着障碍物的最高点转动往前滚动,直到行走轮完全越过障碍物时,此阶段结束。其运动学方程为:
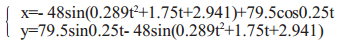
|
(10) |
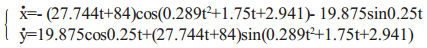
|
(11) |
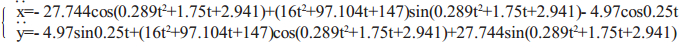
|
(12) |
当行走轮翻越到障碍物最高处的水平位置时,行走轮受行星轮的推动在水平面上做纯滚动,直至行星轮恢复到行走轮最低点为止,即越障机构恢复到水平行走状态。其运动学方程为:

|
(13) |
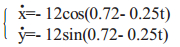
|
(14) |

|
(15) |
根据以上所建立的机器人越障运动学模型的基础,在行走轮大小保持不变的情况下,改变行星轮的半径分别为28.5 mm、31.5 mm和40.5 mm,利用MATLAB对机器人5个阶段的越障轨迹、速度、加速度进行仿真与分析[4]。
图 4是机器人在越障第一阶段的仿真曲线,由于其运动是一匀速直线运动,驱动轮的半径越大,机器人行走的位移越大,速度越快,而加速度则为零。
 |
| 图 4 水平行走阶段仿真曲线 |
图 5是机器人在越障第二阶段的仿真曲线,由于行星轮质心在这一阶段的运动是一规则的圆弧运动,行星轮的半径越大,机器人在该阶段的初速度越大,加速度也越大,而速度则出现了交叉现象。
 |
| 图 5 越障初阶段仿真曲线 |
图 6是机器人在第三个越障阶段的仿真曲线,由于行星轮是沿障碍物的垂直面向上做匀速直线运动,行星轮的半径越大,机器人越障时的位移、速度就越大,而加速度为零。
 |
| 图 6 越障中阶段仿真曲线 |
图 7是机器人在越障第四阶段的仿真曲线,在这一阶段行星轮继续在行走轮内向上爬升,同时行走轮绕障碍物的最高顶点做与行星轮相同的转动。行星轮的半径越大,位移越大、位移变化的梯度越小,速度越小、速度变化的梯度越小,加速度越小、加速度变化的梯度越大。由此表明,行星轮越大,机器人更容易跨越障碍,但半径过大会导致机器人无法翻越障碍。当行星轮的速度为零,行走轮会出现打滑或倒退。驱动轮半径过小会导致机器人的稳定性差,机器人速度波动较大。
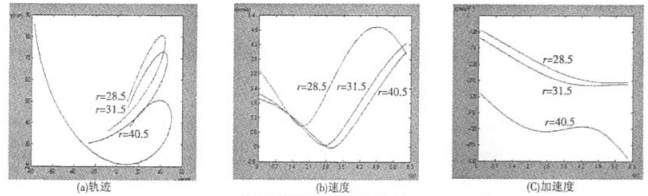 |
| 图 7 越障后阶段仿真曲线 |
图 8是机器人在越障第五阶段的仿真曲线,在这一阶段行星轮继续在行走轮内向上爬升,同时行走轮在障碍物的水平面上做与行星轮相同转向的纯滚动。机器人在此阶段运动轨迹为一段规则的圆弧,速度和加速度大小是恒定的,驱动轮半径越大,其位移、速度和加速度越小。
 |
| 图 8 回复到平底仿真曲线 |
4 结论
(1) 采用行星轮系作为机器人越障行走机构,结构简单,越障能力较强,可以满足工业回转窑衬清理的需要。
(2) 通过对机器人模型进行合理的简化与假设,将机器人的越障过程分为5个阶段,并分别建立了5个阶段的轨迹方程、速度方程和加速度方程,为机器人的运动学仿真奠定了基础。
(3) 从仿真曲线来看,仿真结果与越障理论分析结论一致。通过仿真曲线可知,机器人越障能力与行星轮和行走轮的半径有密切关系。在越障高度不同的情况下,可以根据最优半径比和理论公式反求行走轮、驱动轮的半径,从而可以设计出适应不同要求的越障碍机器人。
| [1] |
蔡自兴.
机器人学[M]. 北京: 清华大学出版社, 2000.
|
| [2] |
李智也. 移动机器人路径规划问题的解决方案[J].
计算机工程, 2006, 32(1): 189–192.
|
| [3] |
霍迎辉, 张连明, 杨宜民. 移动机器人路径规划的最短切线路径算法[J].
广东自动化与信息工程, 2003, 24(1): 10–12.
|
| [4] |
李德君. 机器人仿真技术[J].
现代零部件, 2006(5): 68–69.
|
 2008, Vol. 22
2008, Vol. 22
